js数组深拷贝汇总
1.for 循环实现数组的深拷贝
通过对数组的for循环,即可实现对数组的深拷贝了。
var arr = [1,2,3,4,5]
var arr2 = copyArr(arr)
function copyArr(arr) {let res = []for (let i = 0; i < arr.length; i++) {res.push(arr[i])}return res
}
2.slice 方法实现数组的深拷贝
将原数组中抽离部分出来形成一个新数组。我们只要设置为抽离全部,即可完成数组的深拷贝。
var arr = [1,2,3,4,5]
var arr2 = arr.slice(0)
arr[2] = 5
console.log(arr)
console.log(arr2)
// 输出arr为 [1, 2, 5, 4, 5]
// 输出arr2为 [1, 2, 3, 4, 5]
3.concat 方法实现数组的深拷贝
用于连接多个数组组成一个新的数组的方法。那么,我们只要连接它自己,即可完成数组的深拷贝。
var arr = [1,2,3,4,5]
var arr2 = arr.concat()
arr[2] = 5
console.log(arr)
console.log(arr2)
// 输出arr为 [1, 2, 5, 4, 5]
// 输出arr2为 [1, 2, 5, 4, 5]
4.使用JSON.parse()和JSON.stringify()
const arr1 = [1, 2, 3, 4];
const arr2 = JSON.parse(JSON.stringify(arr1));
5. 使用Array.from()
const arr1 = [1, 2, 3, 4];
const arr2 = Array.from(arr1);
6.使用Array.map()
const arr1 = [1, 2, 3, 4];
const arr2 = arr1.map(item => item);
7.ES6扩展运算符实现数组的深拷贝
var arr = [1,2,3,4,5]
var [ ...arr2 ] = arr
arr[2] = 5
console.log(arr)
console.log(arr2)
// 输出arr为 [1, 2, 5, 4, 5]
// 输出arr2为 [1, 2, 5, 4, 5]
相关文章:

js数组深拷贝汇总
1.for 循环实现数组的深拷贝 通过对数组的for循环,即可实现对数组的深拷贝了。 var arr [1,2,3,4,5] var arr2 copyArr(arr) function copyArr(arr) {let res []for (let i 0; i < arr.length; i) {res.push(arr[i])}return res }2.slice 方法实现数组的深…...
错误 LNK1112 模块计算机类型“x64”与目标计算机类型“X86”冲突
这个错误表明你在进行链接时,模块的计算机类型与目标计算机类型冲突。 在这里,“x64”代表64位系统,“X86”代表32位系统。 要解决这个问题,你需要确保你的所有模块(包括库文件和依赖项)都是与你的目标计…...
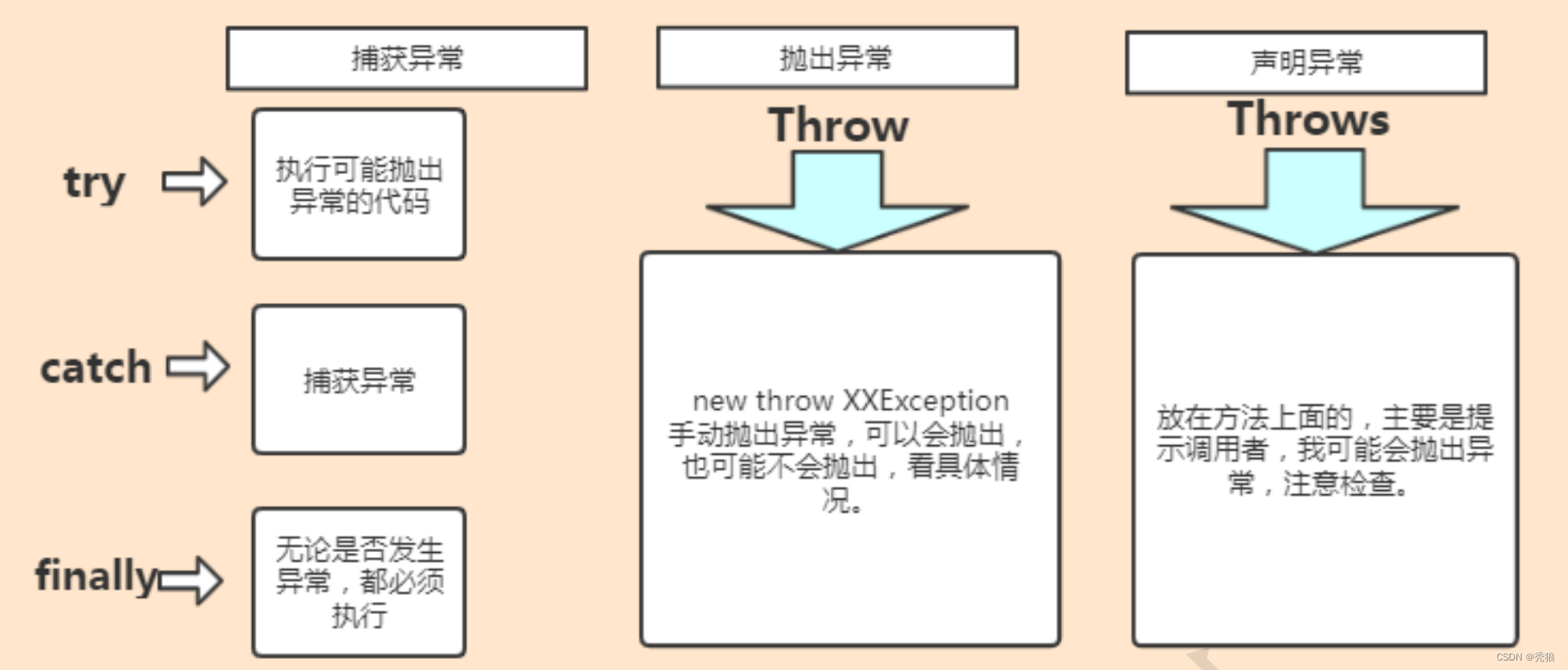
java八股文(基础篇)
面向过程和面向对象的区别 面向过程:在解决问题时,特别自定义函数编写一步一步的步骤解决问题。 面向对象:其特点就是 继承,多态,继承,在解决问题时,不再注重函数的编写,而在于注重…...
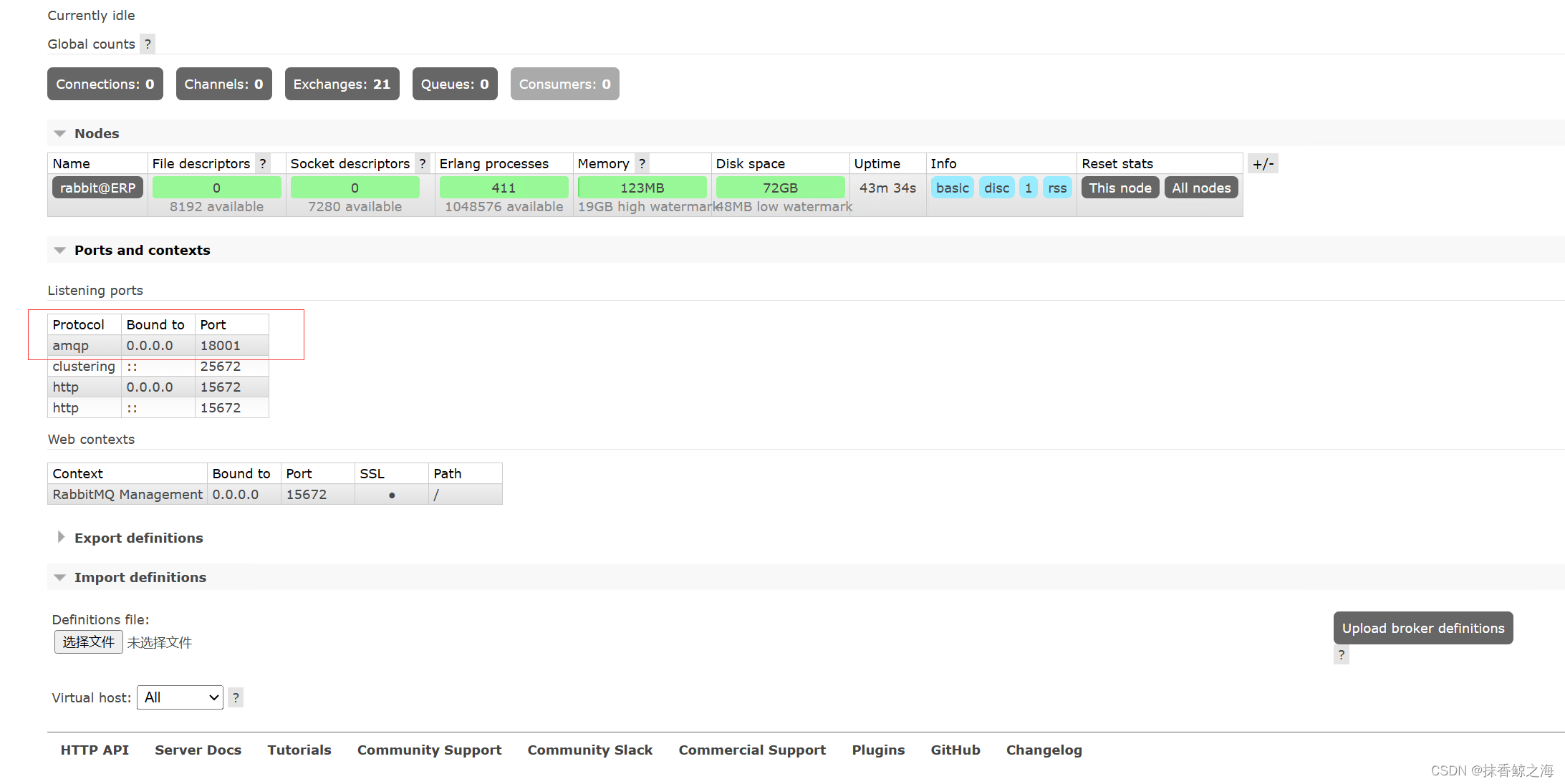
window系统修改rabbitmq 默认端口
安装完rabbitmq之后,默认的client端口是5672, 控制台访问端口是15672,rabbitmq管理工具启动之后在浏览器中输入地址: http://localhost:15672/ 就可以访问后台 , 默认管理员账号:guest 密码&#x…...
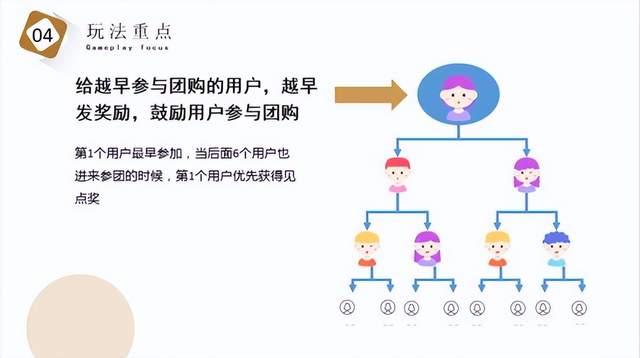
七人拼团模式:颠覆你的购物观念,499元产品让你赚翻天!
七人拼团模式是一种创新的消费模式,通过聚集消费者的购买力,让消费者能够以更优惠的价格购买到优质的商品。下面我们以499元的产品为例,详细介绍七人拼团模式的玩法规则和收益计算。 玩法规则: 消费者购买499元的指定产品后&…...

【机器学习合集】模型设计之卷积核设计 ->(个人学习记录笔记)
文章目录 卷积核设计1. 基于参数压缩的卷积设计1.1 【11卷积】1.2 【11卷积典型应用】1.3 【小卷积的使用】 2. 基于感受野的卷积设计2.1 膨胀卷积(带孔卷积,strous convolution)2.2 可变形卷积2.3 非局部卷积 3. 基于卷积操作的优化3.1 移位网络3.2 加法网络 卷积核…...

JS实现用户二次确认后再提交表单
HTML代码 <form id"importForm" action"" method"post" enctype"multipart/form-data" onsubmit"return confirmSubmit()"> ...... <input id"btnImportSubmit" class"btn btn-primary" type…...
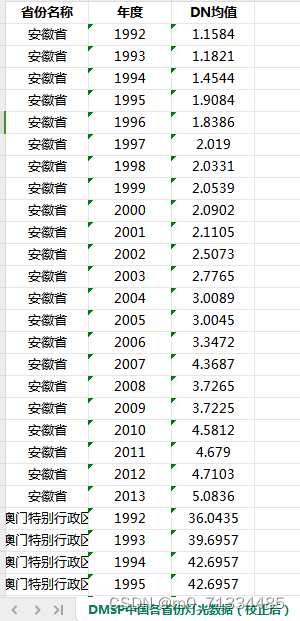
1992-2021年全国各省经过矫正的夜间灯光数据(GNLD、VIIRS)
1992-2021年省市县经过矫正的夜间灯光数据(GNLD、VIIRS) 1、时间:1992-2021年3月,其中1992-2013年为年度数据,2013-2021年3月为月度数据 2、来源:DMSP、VIIRS 3、范围:31省 4、指标解释&…...
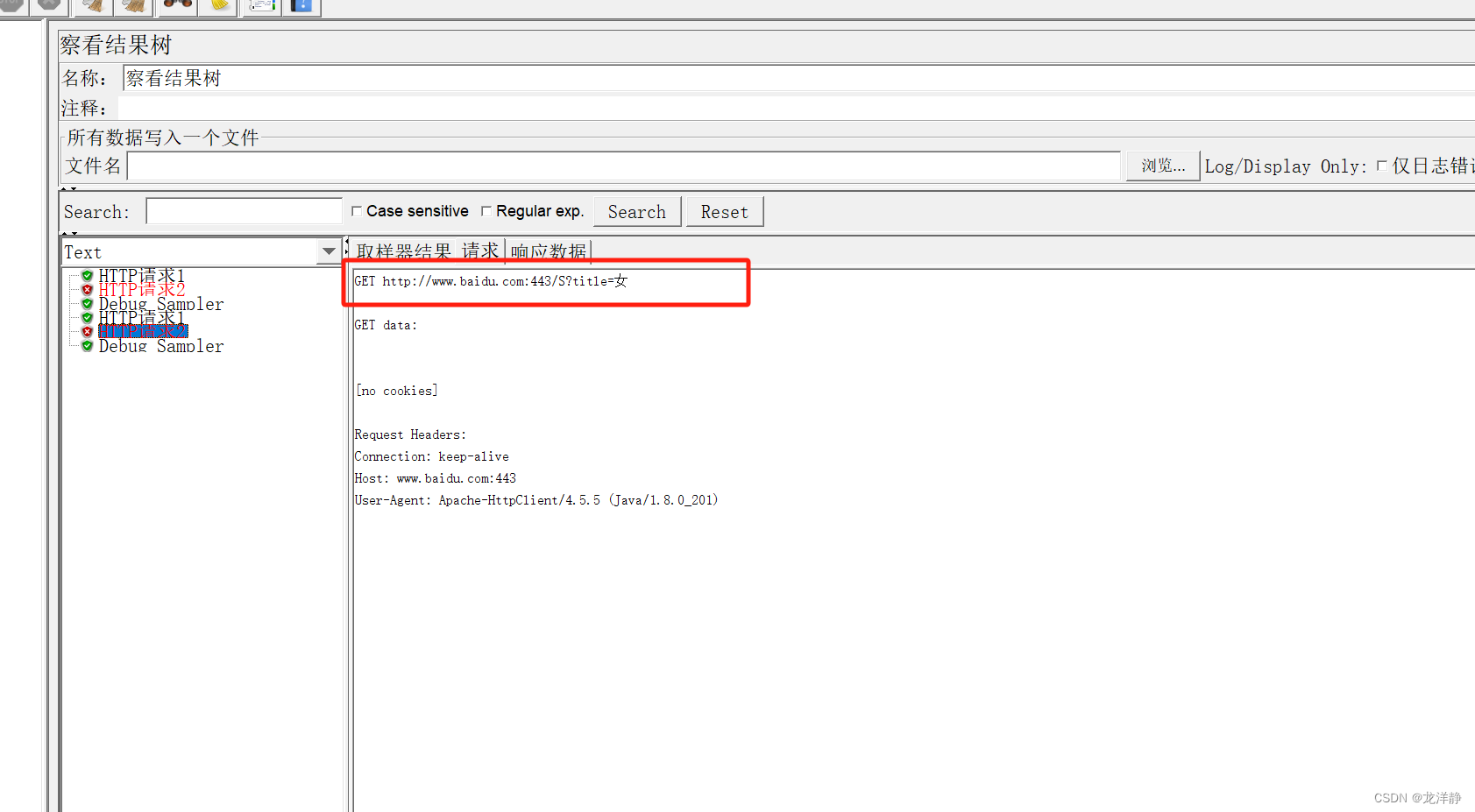
JMeter的使用——傻瓜式学习【中】
目录 前言 1、JMeter参数化 1.1、什么是参数化 1.2、用户定义的变量 1.2.1、什么时候使用用户定义的变量 1.2.2、使用“用户定义的变量”进行参数化的步骤: 1.2.3、案例 1.3、用户参数 1.3.1、什么时候使用用户参数? 1.3.2、使用“用户参数”进…...

MyBaties存储和查询json格式的数据(实体存储查询版本)
最近在做的功能,由于别的数据库有值,需要这边的不同入口的进来查询,所以需要同步过来,如果再继续一个一个生成列对应处理感觉不方便,如果没有别的操作,只是存储和查询,那就可以用MySql支持的jso…...

动态规划14:一和零
动态规划14:一和零 题目 474. 一和零 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。 …...
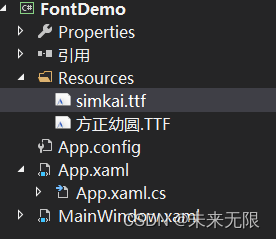
C#WPF嵌入字体实例
本文介绍C#WPF嵌入字体实例。 首先创建项目 添加Resources文件夹,添加字体文件,字体文件属性:生成操作为Resources,复制到输出目录:不复制 字体的使用可以采用以下两种方法: 方式一 直接引用 FontFamily="./Resources/#幼圆" 方式二 定义资源 <Applica…...

Linux——Linux权限
Linux权限 前言一、shell命令以及运行原理二、Linux权限的概念Linux权限管理文件访问者的分类(人)文件类型和访问权限(事物属性)文件权限值的表示方法文件访问权限的相关设置方法 file指令目录的权限粘滞位 总结 前言 linux的学习…...

android中gradle的kotlin编译配置选项
一、编译配置 1、Android中的配置 使用如下方式开启在Android中的gradle的kotlin编译配置: 该配置在其余平台不可用 android {...compileOptions {sourceCompatibility JavaVersion.VERSION_17targetCompatibility JavaVersion.VERSION_17}kotlinOptions {jvmTar…...
【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别))
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

NOIP2023模拟6联测27 点餐
题目大意 有 n n n样菜品,每样菜品都有两个权值 a i a_i ai和 b i b_i bi,如果你选择了 k k k个菜品,分别为 p 1 , … , p k p_1,\dots,p_k p1,…,pk,则你的花费为 ∑ i 1 k a p i max i 1 k b p i \sum\limits_{i…...
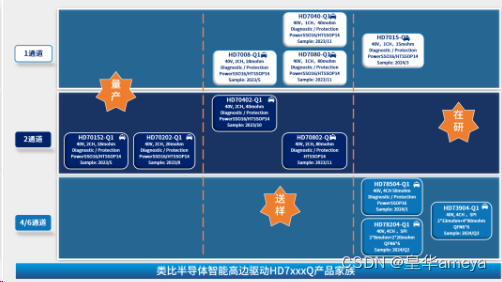
AMEYA360:类比半导体重磅发布车规级智能高边驱动HD7xxxQ系列
致力于提供高品质芯片的国内优秀模拟及数模混合芯片设计商上海类比半导体技术有限公司(下称“类比半导体”或“类比”)宣布推出重磅新品车规级智能高边驱动HD7xxxQ系列。该系列产品包括车规级单通道高边驱动HD70xxQ和车规级双通道智能高边驱动HD70xx2Q,提供不同通道…...

【HarmonyOS】鸿蒙操作系统架构
HarmonyOS架构 一. 鸿蒙系统定位二. 架构整体遵从分层设计三. HarmonyOS具有的技术特性四. HarmonyOS有三大特征 其它相关推荐: 软考系统架构之案例篇(架构设计相关概念) 系统架构之微服务架构 系统架构设计之微内核架构 所属专栏:系统架构设计师 一. 鸿…...
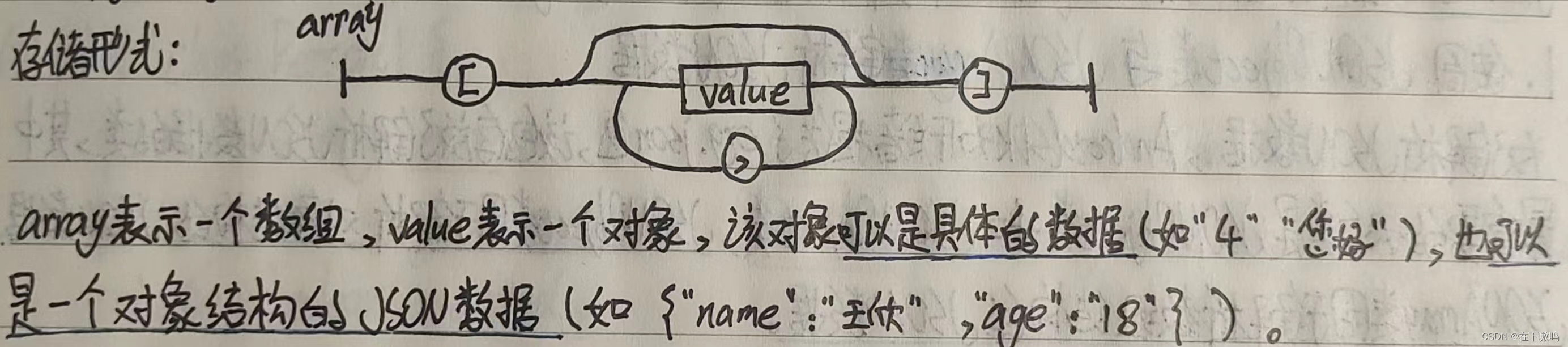
JSON数据
一、JSON介绍 Android应用程序界面上的数据信息大部分都是通过网络请求从服务器上获取到的,获取到的数据类型常见的就是JSON。JSON是一种新的数据格式,这种格式的数据不可以直接显示到程序的界面上,需要将该数据解析为一个集合或对象的形式才…...

金融领域:怎么保持电力系统连续供应?
银行作为金融领域的关键机构,依赖于高度可靠的电力供应,以保持银行操作的连续性。在电力中断或电力质量问题的情况下,银行可能面临严重的风险,包括数据丢失、交易中断和客户满意度下降。 UPS监控系统在这一背景下变得至关重要&…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
