AcWing93. 递归实现组合型枚举:输出从1~n中随机选出的m个整数
题目
从 1∼ n n n 这 n n n 个整数中随机选出 m m m 个,输出所有可能的选择方案。
输入格式
两个整数 n , m , n,m, n,m, 在同一行用空格隔开。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)。
数据范围
n > 0 n>0 n>0,
0 ≤ m ≤ n 0≤m≤n 0≤m≤n,
n + ( n − m ) ≤ 25 n+(n−m)≤25 n+(n−m)≤25
输入样例
5 3
输出样例
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
思考题:如果要求使用非递归方法,该怎么做呢?
思路
思路类似于AcWing92,但是多了一个个数限制。
另外,因为升序排列,所以可以枚举每个数,就可以形成一棵递归搜索树。可以枚举当前在哪层,以及当前以哪个数开始继续往下搜。
代码
#include <bits/stdc++.h>
#include <vector>
using namespace std;vector<int> chosen; //被选择的数void print_subset(int n, int m, int x) {//剪枝:无解的情况//选择超过了m个,或即使再选上剩余的所有数也不够m个,则无解//这条剪枝保证一旦进入无解的分支就会立刻返回if (chosen.size() > m || chosen.size() + (n - x + 1) < m) {return ;}if (x == n + 1) {for (int i = 0; i < chosen.size(); i++) {printf("%d ", chosen[i]);}printf("\n");return ;}//“选num” 分支chosen.emplace_back(x);//记录num已被选择print_subset(n, m, x + 1); 求解子问题chosen.pop_back(); ///回溯到上一问题之前,还原现场//“不选num” 分支print_subset(n, m, x + 1);}int main() {int n, m;scanf("%d%d", &n, &m);print_subset(n, m, 1);return 0;
}
因为剪枝,时间复杂度从 2 n 2^n 2n 降低为 C n m C_n^m Cnm。
递归搜索树写法:
#include <cstdio>
using namespace std;const int N = 30;
int path[N]; //存储路径(选择的数)
int n, m;void dfs(int u, int start) { //u当前层数,start当前在哪个数 if (u > m) { //已经找到了m个数for (int i = 1; i <= m; i++) {printf("%d ", path[i]);}puts("");} else {for (int i = start; i <= n; i++) {path[u] = i; //当前层选择的数是idfs(u + 1, i + 1);path[u] = 0; //恢复现场}}
}int main() {scanf("%d%d", &n, &m);dfs(1, 1);return 0;
}
相关文章:

AcWing93. 递归实现组合型枚举:输出从1~n中随机选出的m个整数
题目 从 1∼ n n n 这 n n n 个整数中随机选出 m m m 个,输出所有可能的选择方案。 输入格式 两个整数 n , m , n,m, n,m, 在同一行用空格隔开。 输出格式 按照从小到大的顺序输出所有方案,每行 1 个。 首先,同一行内的数升序排列&a…...
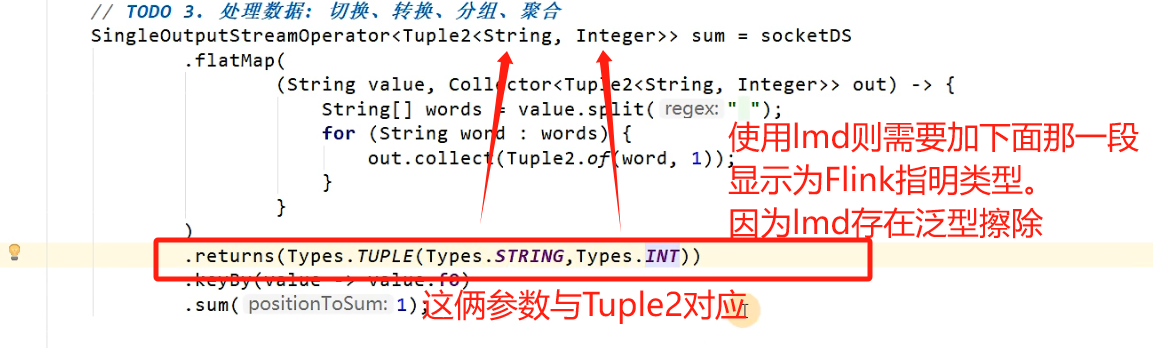
Java修仙传之Flink篇
大道三千:最近我修Flink 目前个人理解: 处理有界,无界流的工具 FLINK: FLINK定义: Flink特点 Flink分层API 流的定义 有界数据流(批处理): 有界流:数据结束了,程序也…...

网络新闻发稿为何经久不衰?
有的老板可能看不到新闻营销的直接回报,一直不乐意在此方面投入,但是却看到竞争对手一直在搞新闻营销,也就安排个PR做做新闻公关。小马识途营销顾问观察,自互联网诞生以来,新闻营销一直是网络营销工作中的一个重点。 如…...

Java SimpleDateFormat 中英文时间格式化转换
SimpleDateFormat是一个以与语言环境有关的方式来格式化和解析日期的具体类。它允许进行格式化(日期 -> 文本)、解析(文本 -> 日期)和规范化。 SimpleDateFormat使得可以选择任何用户定义的日期-时间格式的模式。但是&…...
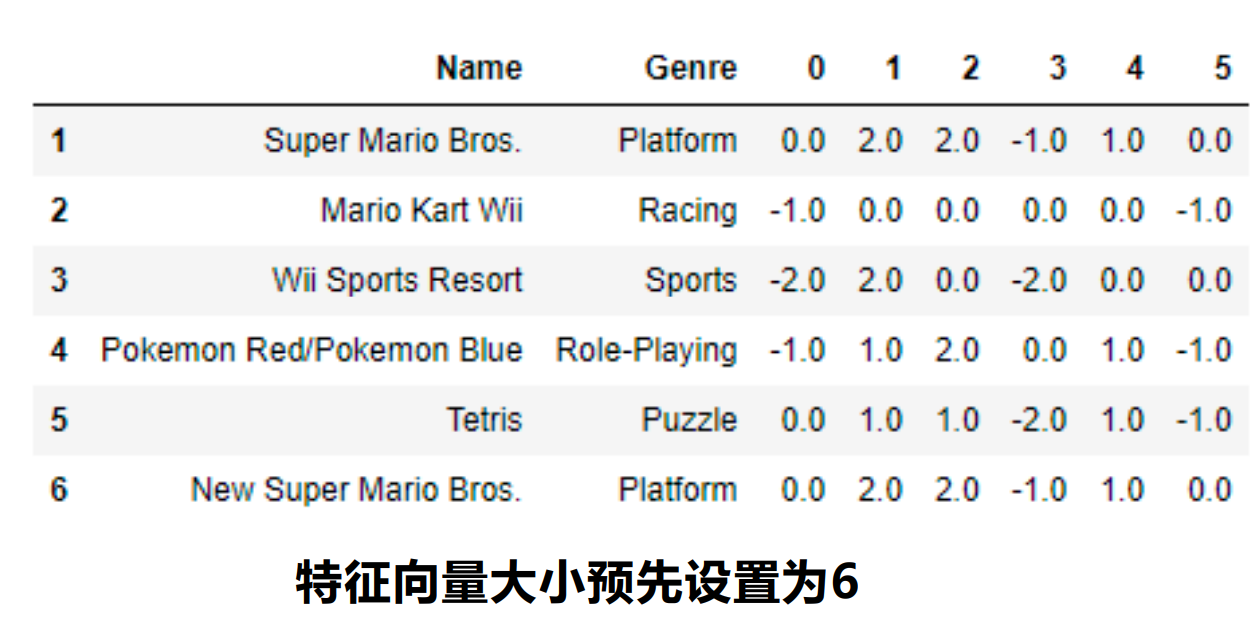
机器学习-基本知识
任务类型 ◼ 有监督学习(Supervised Learning) 每个训练样本x有人为标注的目标t,学习的目标是发现x到t的映射,如分类、回归。 ◼ 无监督学习(Unsupervised Learning) 学习样本没有人为标注,学习的目的是发现数据x本身的分布规律…...
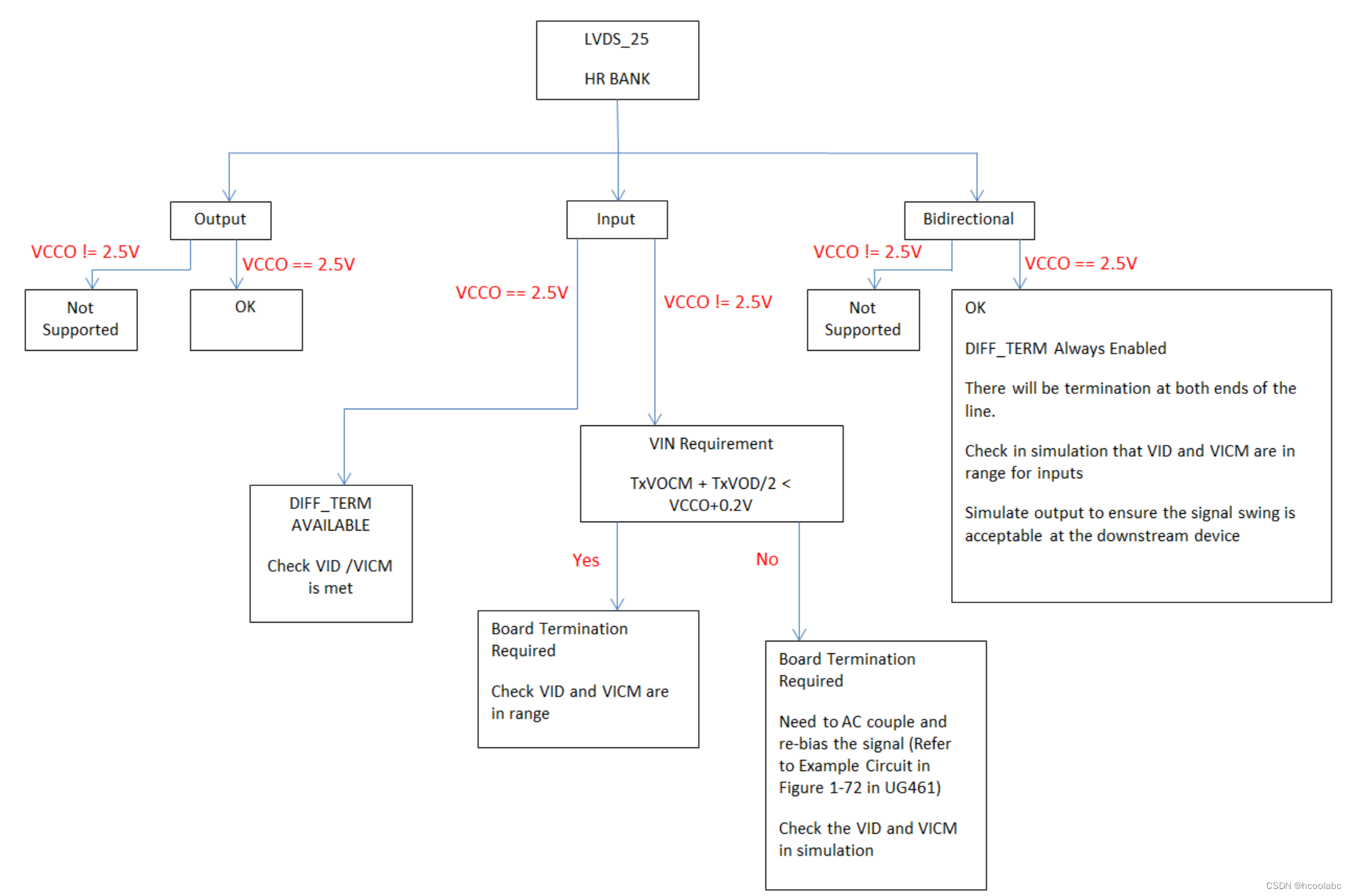
Xilinx 7 系列 1.8V LVDS 和 2.5V LVDS 信号之间的 LVDS 兼容性
如果通过LVDS进行接口,可以按照以程图中的步骤操作,以确保满足正确使用LVDS的所有要求。 40191 - 7 系列 - 1.8V LVDS 和 2.5V LVDS 信号之间的 LVDS 兼容性 与LVDS兼容驱动器和接收器连接时,7系列LVDS和LVDS_25输入和输出应该不存在兼容性问…...
R语言在生态环境领域中的实践技术应用
R语言作为新兴的统计软件,以开源、自由、免费等特点风靡全球。生态环境领域研究内容广泛,数据常多样而复杂。利用R语言进行多元统计分析,从复杂的现象中发现规律、探索机制正是R的优势。为此,以鱼类、昆虫、水文、地形等多样化的生…...
ChineseChess.2023.10.31.01
中国象棋残局模拟器:黑双卒压禁区 中国象棋残局模拟器ChineseChess.2023.10.31.01...

数据库扩展语句和约束方式以及用户管理
数据库扩展语句和约束方式以及用户管理 create TABLE if not exists ky32 ( id int(4) zerofill primary key auto_increment, name varchar(10) not null, cradid int(18) not null unique key, hobby varchar (50) ); auto_increment:表示该字段可以自增长&…...

JMM 简单理解
JMM 简单理解 1 Java 内存模型 Java 内存模型(Java Memory Model,JMM),主要为了屏蔽各种硬件和操作系统的内存差异,以实现让 Java 程序在各种平台下都能达到一致的内存访问效果,而设计的 2 工作内存与主内…...

微软Azure文本转音频,保存成MP3文件【代码python3】
标签: 文本转音频并保存mp3文件; 微软Azure; 微软Azure可以将文本转音频,并保存mp3文件,直接上代码 代码格式:python 3 import os import azure.cognitiveservices.speech as speechsdk# This example re…...

基于单片机的超声波探伤仪设计
摘要 超声波探伤仪是目前工业制造和现代化检测的重要途径之一,广泛的应用在质量检测和产品检测中,通过使用其产品能够有效地降低产品次品的风险。尽管随着电子技术的发展, 国内出现了一些数字化的超声检测仪器,但其数据处理及扩展…...
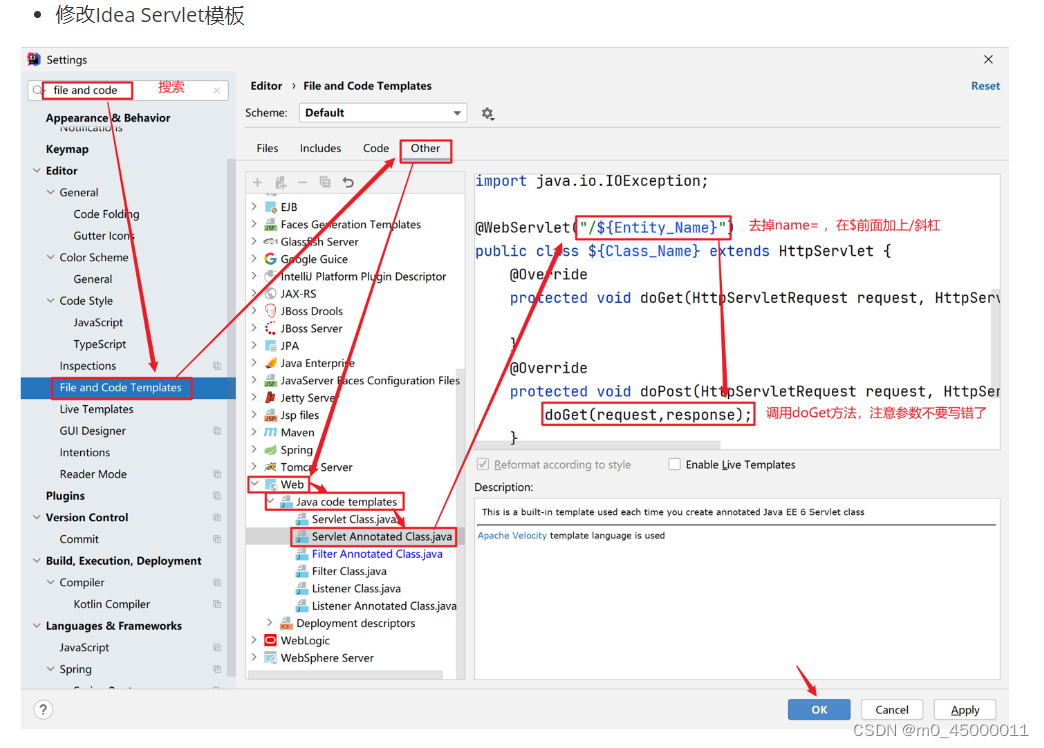
idea的设置
1.设置搜索encoding,所有编码都给换为utf-8 安装插件 eval-reset插件 https://www.yuque.com/huanlema-pjnah/okuh3c/lvaoxt#m1pdA 设置活动模板,idea有两种方式集成tomcat,一种是右上角config配置本地tomcat,一种是插件,如果使用插件集成,则在maven,pom.xml里面加上tomcat…...
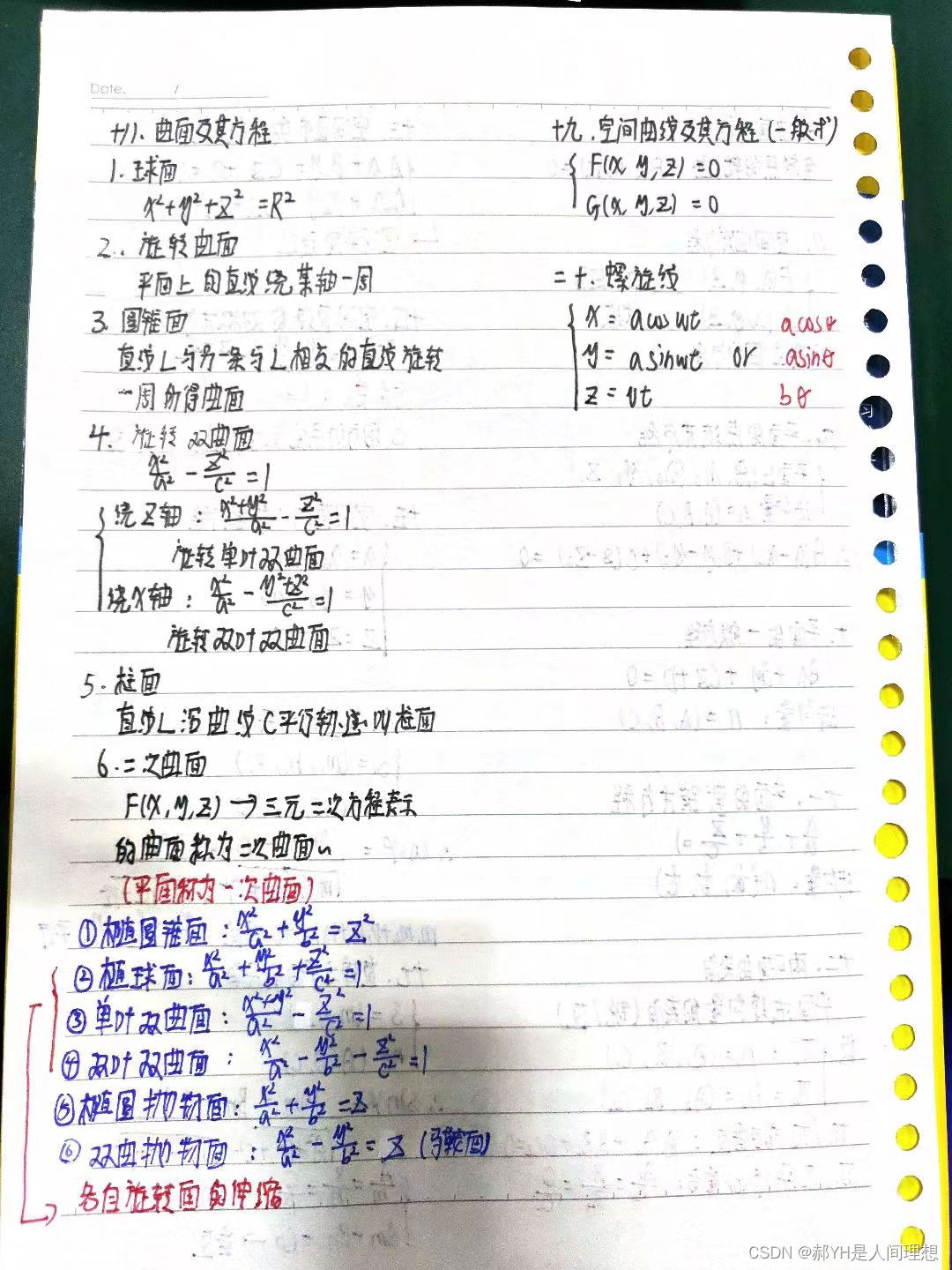
高等数学啃书汇总重难点(八)向量代数与空间解析几何
持续更新,高数下第一章,整体来说比较简单,但是需要牢记公式,切莫掉以轻心~ 一.向量平行的充要条件 二.向量坐标的线性运算 三.向量的几何性质 四.数量积 五.向量积 六.混合积 七.曲面方程 八.空间曲线方程 九.平面的点法式方程 十…...
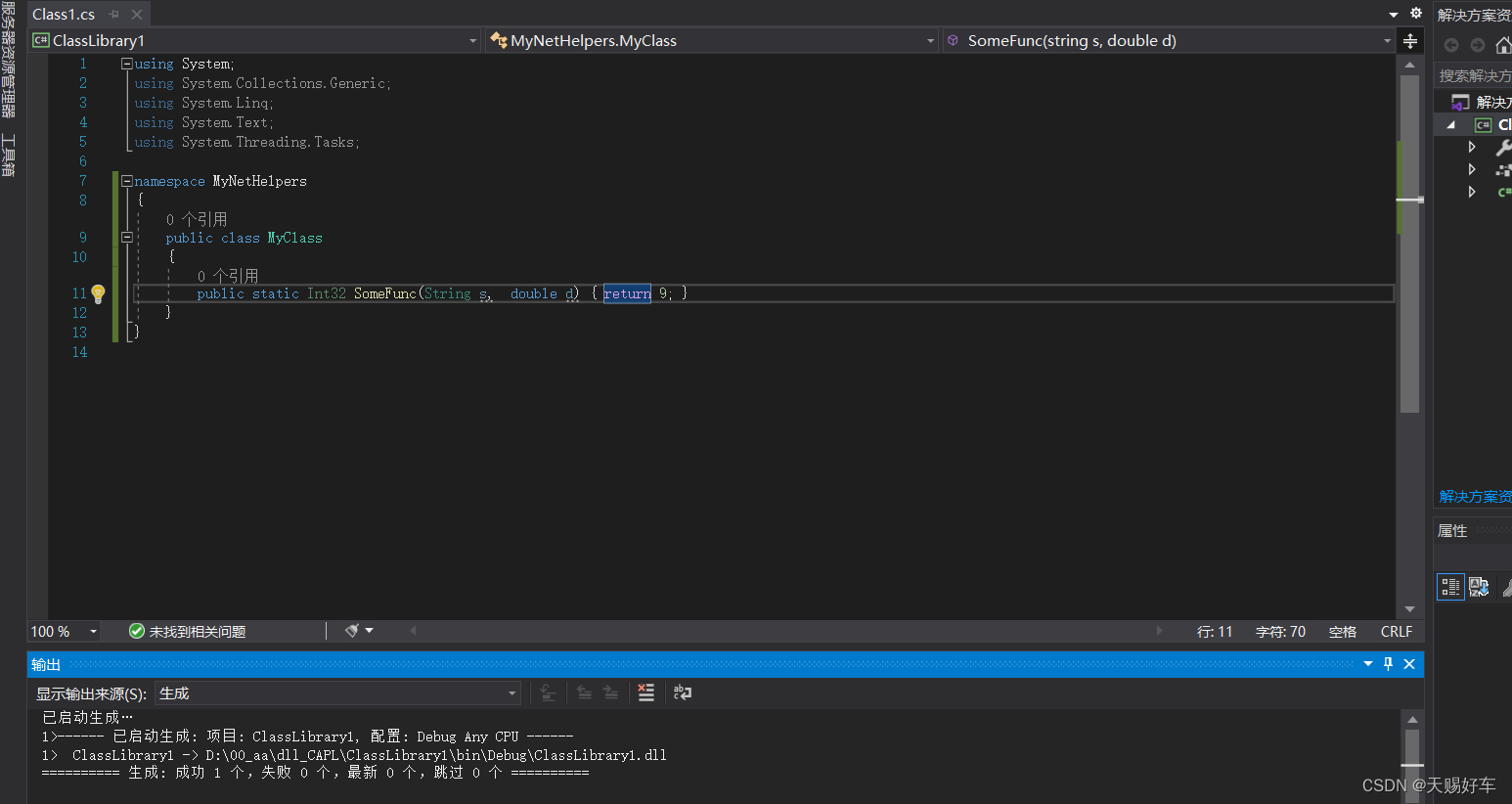
C#开发DLL,CAPL调用(CAPL>> .NET DLL)
文章目录 展示说明新建类库工程C# 代码生成dllCAPL脚本调用dll,输出结果展示 ret为dll里函数返回的值。 说明 新建类库工程 在visual studio中建立。 C# 代码 using...
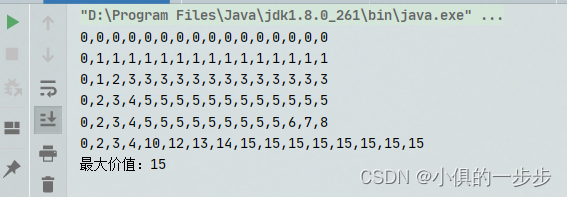
0-1背包问题【穷举法+二维dp数组】
问题描述: 使用穷举法解决0/1背包问题。问题描述:给定n个重量为{w1, w2, … ,wn}、价值为{v1, v2, … ,vn} 的物品和一个容量为C的背包,求这些物品中的一个最有价值的子集,且要能够装到背包中。 穷举法:每件物品装还是…...
nodejs+vue+python+php基于微信小程序的在线学习平台设计与实现-计算机毕业设计
困扰管理层的许多问题当中,在线学习也是不敢忽视的一块。但是管理好在线学习又面临很多麻烦需要解决,例如:如何在工作琐碎,记录繁多的情况下将在线学习的当前情况反应给课程问题管理员决策,等等。 流,开发一个在线学习平台小程序一方面的可能会更合乎时宜,另一方面来…...
Spring学习笔记2 Spring的入门程序
Spring学习笔记1 启示录_biubiubiu0706的博客-CSDN博客 Spring官网地址:https://spring.io 进入github往下拉 用maven引入spring-context依赖 写spring的第一个程序 引入下面依赖,好比引入Spring的基本依赖 <dependency><groupId>org.springframework</groupId&…...
)
【Linux】虚拟机安装Linux、客户端工具及Linux常用命令(详细教程)
一、导言 1、引言 Linux是一个开源的操作系统内核,它最初由芬兰计算机科学家Linus Torvalds于1991年开发。Linux不同于传统的商业操作系统,它常用于服务器、嵌入式系统和个人电脑等各种平台。 Linux具有很多优点,包括稳定性、安全性和可定制…...

Day 47 动态规划 part13
Day 47 动态规划 part13 解题理解300674718 3道题目 300. 最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 解题理解 300 dp[i]被设置为以nums[i]为结尾的最长递增子序列长度。 class Solution:def lengthOfLIS(self, nums: List[int]) -> int:if len(nums) …...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
