当前位置： 首页 > news >正文

css 某个元素被挤的显示不完整，如何显示完整

news 2026/2/9 1:04:26

加一行

flex-shrink: 0;

解决

相关文章：

css 某个元素被挤的显示不完整，如何显示完整

加一行 flex-shrink: 0;解决...

编程日记 2023/10/31 22:47:53

pve lxc debian 11安装docker遇到bash: sudo: command not解决办法

pve创建LXC容器，使用debian 11模版，安装完成后正常换源、安装依赖 然后添加Docker 的官方 GPG 密钥时出错： $ curl -fsSL https://mirrors.ustc.edu.cn/docker-ce/linux/debian/gpg | sudo apt-key add - 提示 bash: sudo: command not …...

编程日记 2023/10/31 22:46:52

springboot的缓存和redis缓存，入门级别教程

一、springboot（如果没有配置）默认使用的是jvm缓存 1、Spring框架支持向应用程序透明地添加缓存。抽象的核心是将缓存应用于方法，从而根据缓存中可用的信息减少执行次数。缓存逻辑是透明地应用的，对调用者没有任何干扰。只要使用…...

编程日记 2023/10/31 22:45:50

语雀P0级时间爆发，留给运维的时间不多了？

事件背景 打工人的焦虑，已经延伸到在线文档了。近日，语雀P0级故障想必大家都有所体会，宕机近8小时，笔记、离线同步完全不可用。作为用户尤其担心我的文档资料是否会因此消失。 这泼天的8小时，放眼互联网界也是相当炸裂…...

编程日记 2023/10/31 22:42:48

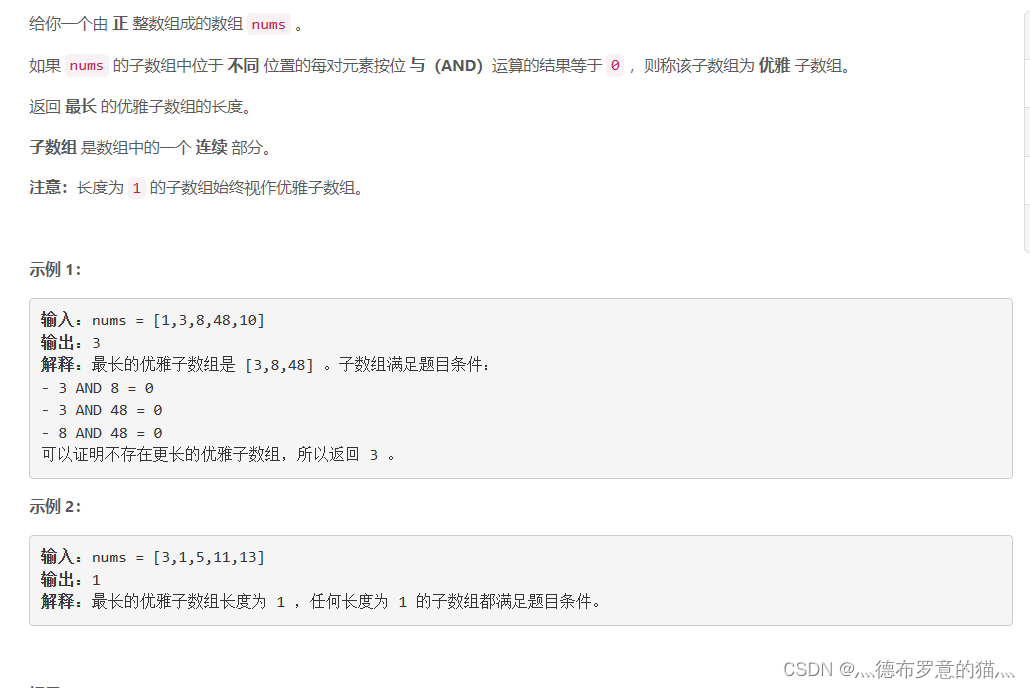
LeetCode 2401.最长优雅子数组 ----双指针+位运算

数据范围1e5 考虑nlog 或者n的解法&#xff0c;考虑双指针 因为这里要求的是一段连续的数组 想起我们的最长不重复连续子序列 然后结合一下位运算就好了 是一道双指针不错的题目 class Solution { public:int longestNiceSubarray(vector<int>& nums) {int n nums…...

编程日记 2023/10/31 22:41:47

NOIP2023模拟6联测27 无穷括号序列

题目大意 小 C C C有一个括号序列 A A A&#xff0c;其长度为 m m m&#xff0c;且序列元素只包含左右括号。他想生成一个无限长的括号序列 B B B&#xff0c;由于 B B B的长度为正无穷&#xff0c;所以其下标可以为任意整数&#xff08;可以为负&#xff09;。为了由 A A A生…...

编程日记 2023/10/31 22:40:46

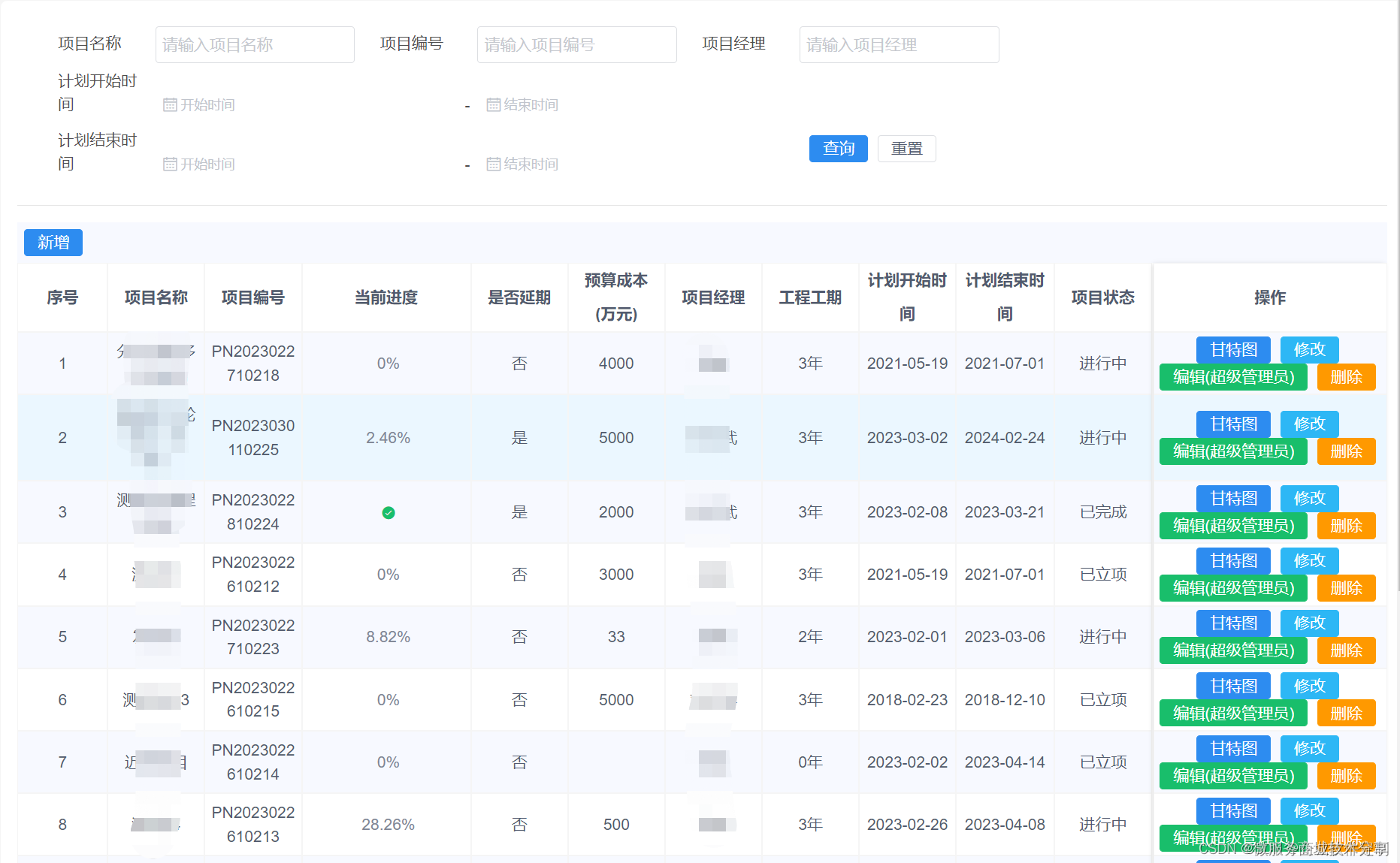
java spring cloud 工程企业管理软件-综合型项目管理软件-工程系统源码

Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下&#xff1a; 首页 工作台&#xff1a;待办工作、消息通知、预警信息&#xff0c;点击可进入相应的列表 项目进度图表&#xff1a;选择&#xff08;总体或单个&#xff09;项目显示…...

编程日记 2023/10/31 22:39:44

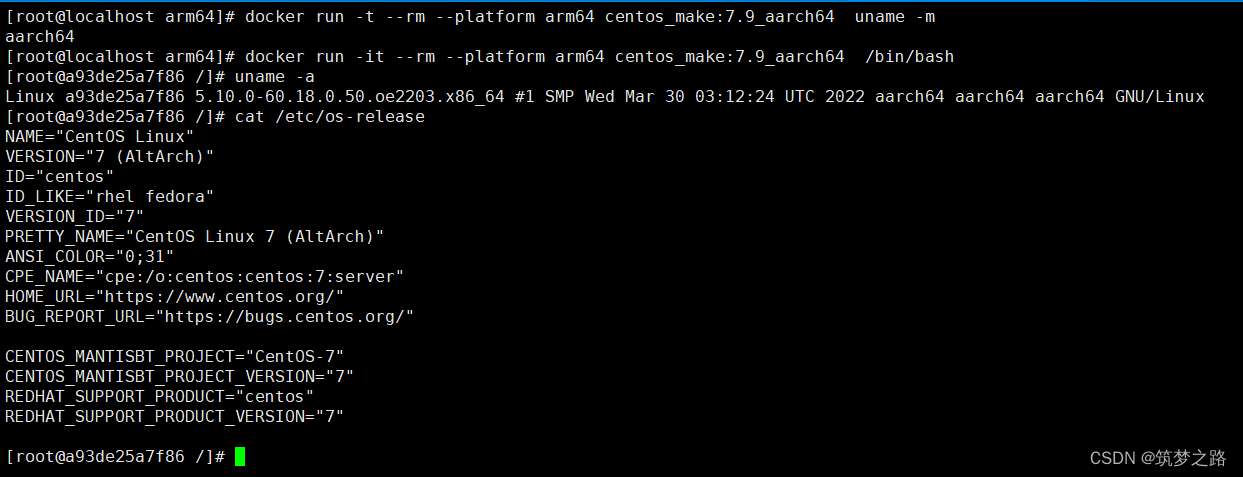
openEuler 22.03 x86架构下docker运行arm等架构的容器——筑梦之路

为什么要这样做&#xff1f; 随着国产化的普及&#xff0c;国家政策对信创产业的支持&#xff0c;尤其一些金融证券行业、政府单位等&#xff0c;逐渐开始走国产化信创的路线&#xff0c;越来越多接触到国产 CPU &#xff08;arm 平台&#xff0c;比如华为的鲲鹏处理器&#xf…...

编程日记 2023/10/31 22:38:43

【Java】HashMap常见的面试题

HashMap常见面试题 1.HashMap key 是否可以是为 我们自定义对象&#xff1f;——可以 2.HashMap 存储数据 有序还是无序&#xff1f;——无序 3.HashMap key 是否可以存放 null值&#xff1f;如果可以的话 存放在 数组中那个位置&#xff1f;——可以;存放在 index0的位置 4.Ha…...

编程日记 2023/10/31 22:37:42

openpnp - src - 配置文件载入过程的初步分析

文章目录 openpnp - src - 配置文件载入过程的初步分析概述笔记自己编译用的git版本报错截图问题1 - 怎么在调试状态下, 定位到抛异常的第一现场?结合单步调试找到的现场, 来分析报错的原因openpnp配置文件读取的流程END openpnp - src - 配置文件载入过程的初步分析 概述 从…...

编程日记 2023/10/31 22:36:41

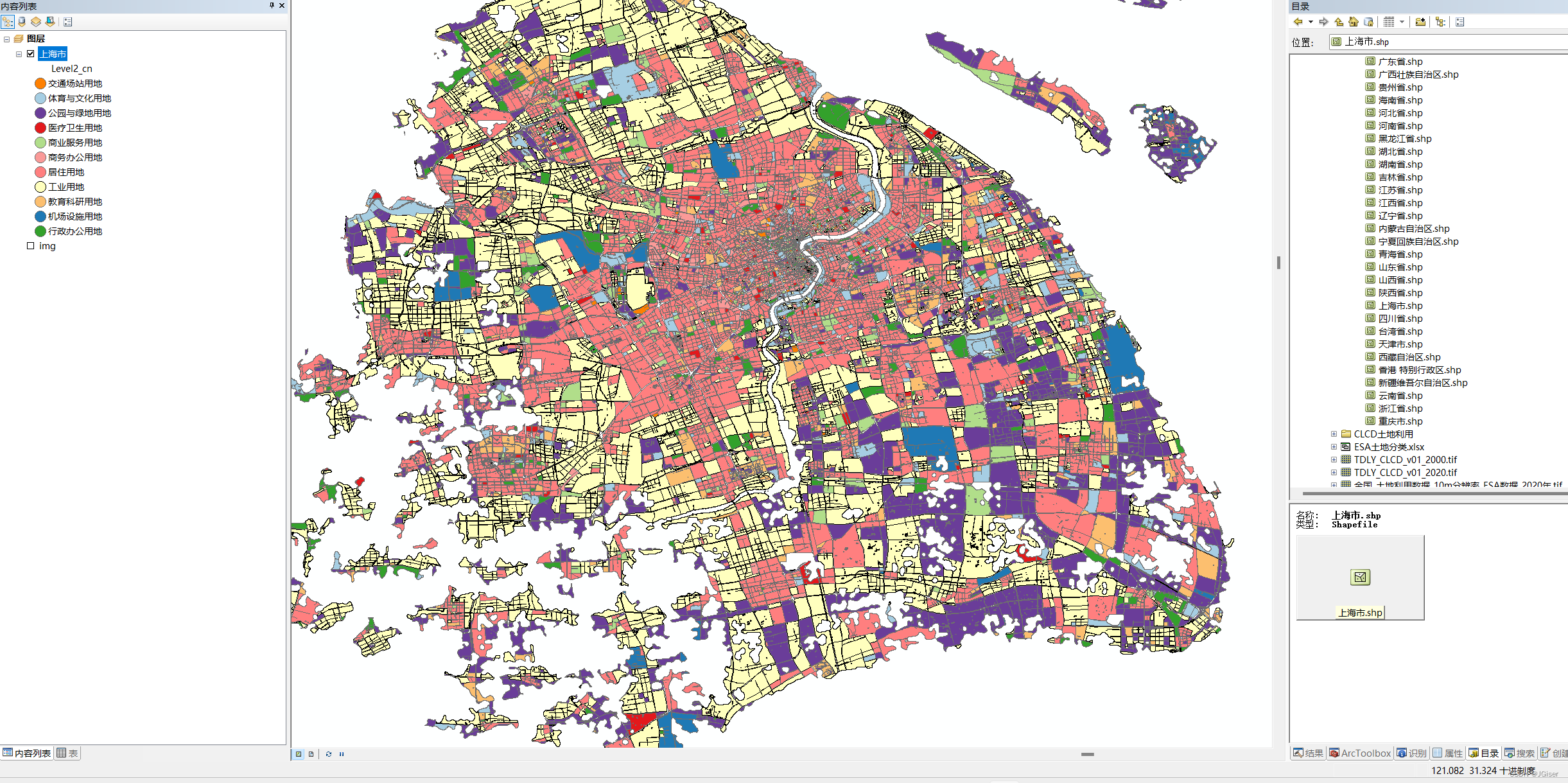
中国各城市土地利用类型（城市功能）数据集（shp）

中国各城市土地利用类型（城市功能）数据集 时间：2018年 全国范围的城市用地类型数据（居住/商业/交通用地等共计11类） 分类：居住用地、商业用地、工业用地、医疗设施用地、体育文化设施用地、交通场站用地、绿地等用地类型 含城市编码、一级分类5个、二级分类11个 数据按…...

编程日记 2023/10/31 22:35:40

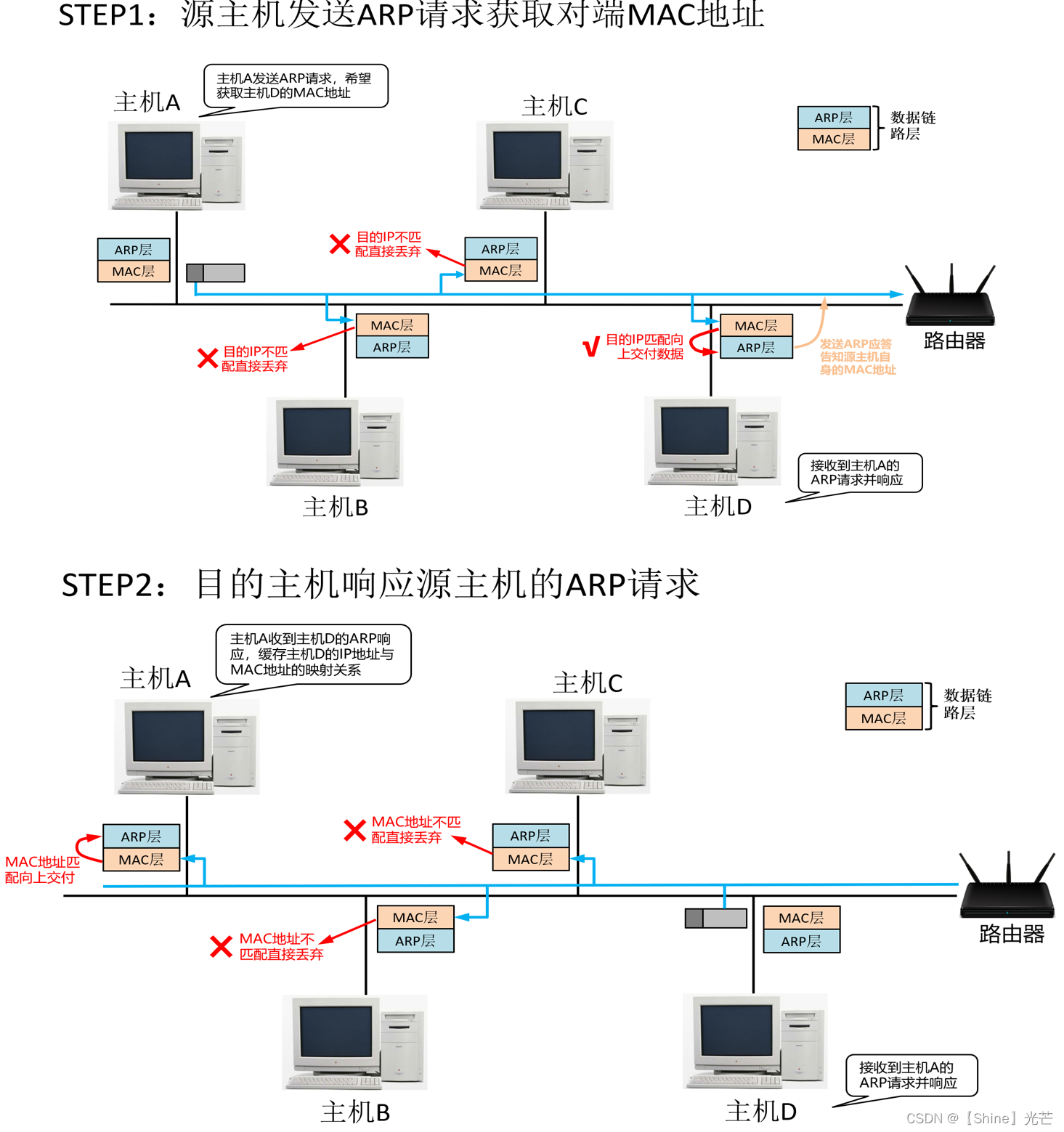
Linux网络编程：数据链路层

目录 一. 数据链路层概述 二. 以太网 2.1 以太网的概念 2.2 以太网数据帧 2.3 对于MAC地址的认识 2.4 数据碰撞问题 三. MTU和MSS 3.1 什么是MTU 3.2 MTU对UDP的影响 3.3 MTU对TCP的影响&#xff08;MSS的概念&#xff09; 四. ARP协议 4.1 ARP协议的作用 4.2 ARP数…...

编程日记 2023/10/31 22:34:39

python 线程 超时时间

python 线程 超时时间_mob649e815f0f18的技术博客_51CTO博客...

编程日记 2023/10/31 22:33:37

LeetCode：274. H 指数、275. H 指数 II（C++）

目录 274. H 指数 题目描述&#xff1a; 实现代码与解析&#xff1a; 排序暴力 275. H 指数 II 题目描述&#xff1a; 实现代码与解析&#xff1a; 二分 比较简单&#xff0c;不再写解析&#xff0c;注意二分的时候&#xff0c;r指针为n&#xff0c;含义为个数&#xf…...

编程日记 2023/10/31 22:32:36

多线程及锁

1.lock锁和synchronized锁的区别。 1&#xff1a;Synchronized 是Java的一个关键字&#xff0c;而Lock是java.util.concurrent.Locks 包下的一个接口&#xff1b; 2&#xff1a;Synchronized 使用过后&#xff0c;会自动释放锁&#xff0c;而Lock需要手动上锁、手动释放锁&am…...

编程日记 2023/10/31 22:30:33

C++ 写一个Data类的注意问题

Data类 声明和定义分离的一些问题 声明里面我们不带缺省参数&#xff0c;定义我们给缺省参数&#xff0c;如下面两段代码&#xff1a; Data.h#pragma once #include<iostream> using namespace std; class Data { public:Data(int year,int month,int day);private:in…...

编程日记 2023/10/31 22:29:32

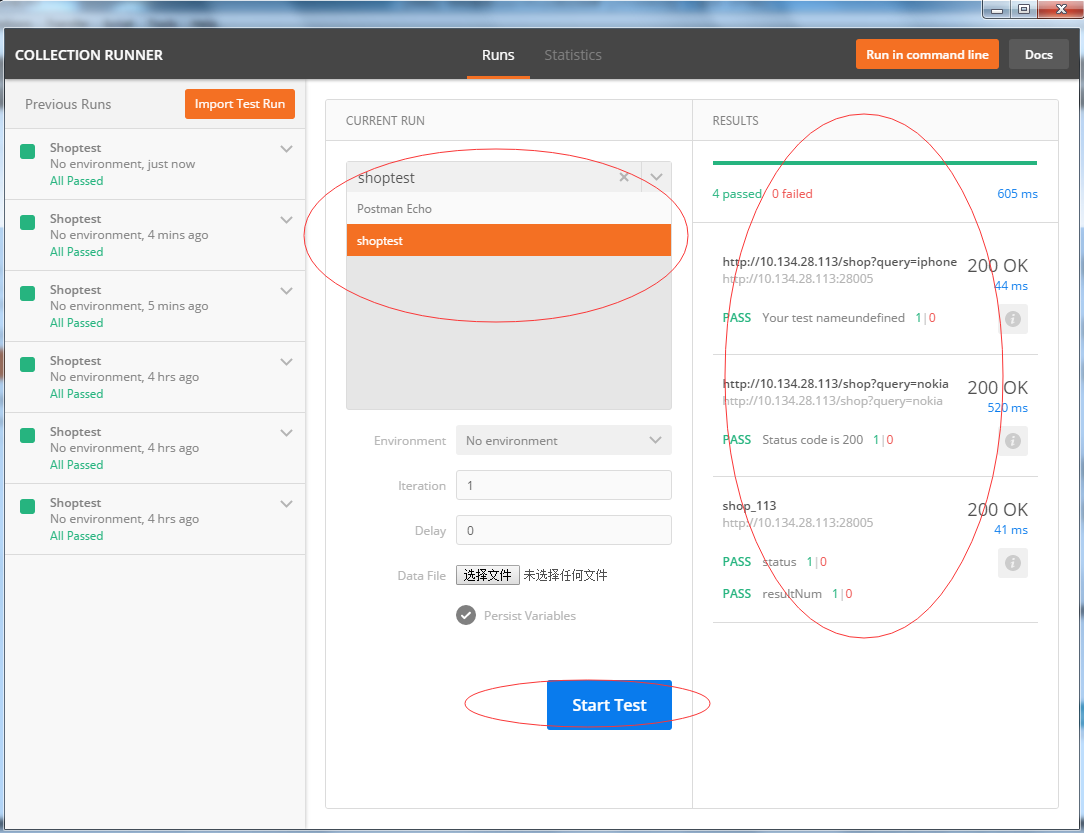
postman做接口测试

之前搞自动化接口测试&#xff0c;由于接口的特性&#xff0c;要验证接口返回xml中的数据&#xff0c;所以没找到合适的轮子&#xff0c;就自己用requests造了个轮子&#xff0c;用着也还行&#xff0c;不过就是case管理有些麻烦&#xff0c;近几天又回头看了看postman也可以玩…...

编程日记 2023/10/31 22:28:31

hdlbits系列verilog解答（always块）-29

文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 由于数字电路由用网线连接的逻辑门组成，因此任何电路都可以表示为模块和赋值语句的某种组合。然而，有时这不是描述电路的最方便方式。过程procedure（其中 always 的块就是一个示例）提供了描述电路的替代语法…...

编程日记 2023/10/31 22:27:30

uniapp实现瀑布流

首先我们要先了解什么是瀑布流&#xff1a; 瀑布流&#xff08;Waterfall Flow&#xff09;是一种常见的网页布局方式&#xff0c;也被称为瀑布式布局或砌砖式布局。它通常用于展示图片、博客文章、商品等多个不同大小和高度的元素。 瀑布流布局的特点是每个元素按照从上到下…...

编程日记 2023/10/31 22:25:28

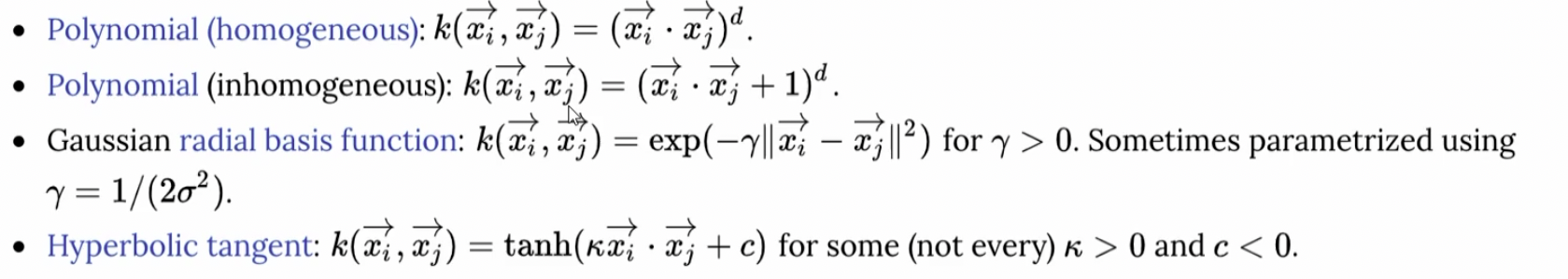
15. 机器学习 - 支持向量机

Hi, 你好。我是茶桁。 逻辑回归预测心脏病 在本节课开始呢&#xff0c;我给大家一份逻辑回归的练习&#xff0c;利用下面这个数据集做了一次逻辑回归预测心脏病的练习。 本次练习的代码在「茶桁的AI秘籍」在Github上的代码库内&#xff0c;数据集的获取在文末。这样做是因为我…...

编程日记 2023/10/31 22:24:26

C++ 求圆面积的程序（Program to find area of a circle）

给定半径r&#xff0c;求圆的面积。圆的面积应精确到小数点后5位。 例子&#xff1a; 输入&#xff1a;r 5 输出&#xff1a;78.53982 解释&#xff1a;由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982&#xff0c;因为我们只保留小数点后 5 位数字。 输…...

编程新知 2026/1/31 12:52:15

NLP学习路线图（二十三）：长短期记忆网络（LSTM）

在自然语言处理（NLP）领域，我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感，还是实现语言的翻译，都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心，而循环神经网络（RNN） 曾被视为…...

编程新知 2026/2/1 7:05:28

使用 SymPy 进行向量和矩阵的高级操作

在科学计算和工程领域&#xff0c;向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能&#xff0c;能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作&#xff0c;并通过具体…...

编程新知 2026/2/8 21:52:30

ip子接口配置及删除

配置永久生效的子接口&#xff0c;2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

编程新知 2025/10/26 5:04:25

Mobile ALOHA全身模仿学习

一、题目 Mobile ALOHA&#xff1a;通过低成本全身远程操作学习双手移动操作 传统模仿学习&#xff08;Imitation Learning&#xff09;缺点&#xff1a;聚焦与桌面操作&#xff0c;缺乏通用任务所需的移动性和灵活性 本论文优点&#xff1a;&#xff08;1&#xff09;在ALOHA…...

编程新知 2026/1/27 14:18:20

Pinocchio 库详解及其在足式机器人上的应用

Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库&#xff0c;专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性&#xff0c;并提供了一个通用的框架&…...

编程新知 2025/11/28 5:32:31

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2026/1/29 14:27:00

SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题

分区配置 (ptab.json) img 属性介绍&#xff1a; img 属性指定分区存放的 image 名称&#xff0c;指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件&#xff0c;则以 proj_name:binary_name 格式指定文件名&#xff0c; proj_name 为工程 名&…...

编程新知 2026/1/23 10:51:19

纯 Java 项目（非 SpringBoot）集成 Mybatis-Plus 和 Mybatis-Plus-Join

纯 Java 项目&#xff08;非 SpringBoot&#xff09;集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

编程新知 2025/9/26 12:26:35

怎么让Comfyui导出的图像不包含工作流信息，

为了数据安全&#xff0c;让Comfyui导出的图像不包含工作流信息&#xff0c;导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo&#xff08;推荐&#xff09;​​ 在 save_images 方法中&#xff0c;​​删除或注释掉所有与 metadata …...

编程新知 2025/8/13 15:12:54