【每日一题Day364】LC2003每棵子树内缺失的最小基因值 | dfs
每棵子树内缺失的最小基因值【LC2003】
有一棵根节点为
0的 家族树 ,总共包含n个节点,节点编号为0到n - 1。给你一个下标从 0 开始的整数数组parents,其中parents[i]是节点i的父节点。由于节点0是 根 ,所以parents[0] == -1。总共有
105个基因值,每个基因值都用 闭区间[1, 105]中的一个整数表示。给你一个下标从 0 开始的整数数组nums,其中nums[i]是节点i的基因值,且基因值 互不相同 。请你返回一个数组
ans,长度为n,其中ans[i]是以节点i为根的子树内 缺失 的 最小 基因值。节点
x为根的 子树 包含节点x和它所有的 后代 节点。
-
思路
本题关键点在于
- 如果树中不存在节点基因值为1的点,那么所有节点缺失的最小基因值为1
- 如果树中存在节点基因值为1的点,那么其祖先节点缺失的最小基因值不为1,其他节点均为1
那么,如果树中有基因值为1的节点的话,从该节点出发dfs求出其祖先节点缺失的最小基因值
- dfs过程中使用哈希表记录目前已经遍历的基因值
- 使用变量记录当前缺失的最小基因值
-
实现
class Solution {public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {int n = parents.length;int[] ans = new int[n];Arrays.fill(ans, 1);int node = -1;for (int i = 0; i < n; i++) {if (nums[i] == 1) {node = i; // 出发点break;}}if (node < 0) { // 不存在基因值为 1 的点return ans;}// 建树List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for (int i = 1; i < n; ++i) {g[parents[i]].add(i);}Set<Integer> vis = new HashSet<>();int mex = 2; // 缺失的最小基因值while (node >= 0) {dfs(node, g, vis, nums);while (vis.contains(mex)) { // node 子树包含这个基因值mex++;}ans[node] = mex; // 缺失的最小基因值node = parents[node]; // 往上走}return ans;}// 遍历 x 子树private void dfs(int x, List<Integer>[] g, Set<Integer> vis, int[] nums) {vis.add(nums[x]); // 标记基因值for (int son : g[x]) {if (!vis.contains(nums[son])) {dfs(son, g, vis, nums);}}} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/smallest-missing-genetic-value-in-each-subtree/solutions/2505883/tu-jie-yi-zhang-tu-miao-dong-duo-chong-x-q095/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度: O ( n ) \mathcal{O}(n) O(n), n n n为二叉树的节点数目,每个节点最多只会访问1次
- 空间复杂度: O ( n + m ) \mathcal{O}(n+m) O(n+m)
- 复杂度
相关文章:

【每日一题Day364】LC2003每棵子树内缺失的最小基因值 | dfs
每棵子树内缺失的最小基因值【LC2003】 有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parent…...
 程序烧写完成但是没有现象 (自己做的板子))
调试记录 单片机GD32F103C8T6(兆易创新) 程序烧写完成但是没有现象 (自己做的板子)
1. 单片机GD32F103C8T6 的资料 CPU内核:ARM Cortex-M3 CPU最大主频:108MHz 工作电压范围:2.6V~3.6V 程序存储容量:64KB 程序存储器类型:FLASH RAM, 总容量:20KB GPIO端口数量:37 最…...

Leetcode刷题笔记--Hot91--100
1--汉明距离(461) 主要思路: 按位异或,统计1的个数; #include <iostream> #include <vector>class Solution { public:int hammingDistance(int x, int y) {int z x ^ y; // 按位异或int res 0;while(…...

算法训练一——链表
文章目录 已做...

【JAVA】类与对象的重点解析
个人主页:【😊个人主页】 系列专栏:【❤️初识JAVA】 文章目录 前言类与对象的关系JAVA源文件有关类的重要事项static关键字 前言 Java是一种面向对象编程语言,OOP是Java最重要的概念之一。学习OOP时,学生必须理解面向…...

ES6对象扩展
ES6对象扩展是指在ES6中新增的一些对象属性和方法,包括对象属性的简写、计算属性名、对象方法的简写、对象的可迭代性、拓展运算符等。 下面是一些常用的ES6对象扩展: 对象属性的简写 ES6中,当对象的属性名和赋值变量名相同时,…...
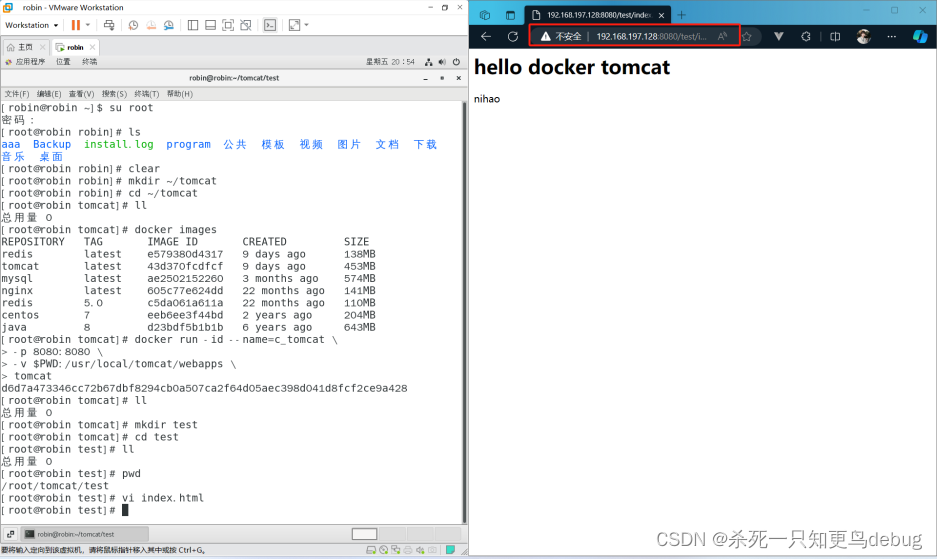
docker应用部署---Tomcat的部署配置
1. 搜索tomcat镜像 docker search tomcat2. 拉取tomcat镜像 docker pull tomcat3. 创建容器,设置端口映射、目录映射 # 在/root目录下创建tomcat目录用于存储tomcat数据信息 mkdir ~/tomcat cd ~/tomcatdocker run -id --namec_tomcat \ -p 8080:8080 \ -v $PWD:…...

TestCenter测试管理工具
estCenter(简称TC)一款广受好评的测试管理工具,让测试工作更规范、更有效率,实现测试流程无纸化,测试数据资产化。 产品概述 TC流程图 产品功能 一、案例库 案例库集中化管理,支持对测试用例集中管理&…...

索引切片复习
# loc方法 data2.loc[:4,[ymd, bWendu]]# iloc方法 —— 连续取字段 data2.iloc[:4,1:3]# iloc方法 —— 非连续取字段 data2.iloc[:4,[1,4]]# 直接选取单个字段 —— Series data2[ymd]# 直接选取单个字段 —— DataFrame data2[[ymd]]# 直接选取多个字段 —— DataFrame data…...

想入门网络安全,这些前置准备要做好!
网上有很多关于网络安全如何学习、如何入门的内容,但是仍然有很多小白不懂网络安全要怎么去学习。这是由于网络安全包含的范围确实比较广,学习的内容也比较多,所以在刚开始了解的时候确实会有点搞不清楚状况。 这里有一个方法,不要…...

Spark新特性与核心概念
一、Sparkshuffle (1)Map和Reduce 在shuffle过程中,提供数据的称之为Map端(Shuffle Write),接受数据的称之为Redeuce端(Shuffle Read),在Spark的两个阶段中,总…...
设计模式_状态模式
状态模式 介绍 设计模式定义案例问题堆积在哪里解决办法状态模式一个对象 状态可以发生改变 不同的状态又有不同的行为逻辑游戏角色 加载不同的技能 每个技能有不同的:攻击逻辑 攻击范围 动作等等1 状态很多 2 每个状态有自己的属性和逻辑每种状态单独写一个类 角色…...

css 某个元素被挤的显示不完整,如何显示完整
加一行 flex-shrink: 0;解决...

pve lxc debian 11安装docker遇到bash: sudo: command not解决办法
pve创建LXC容器,使用debian 11模版,安装完成后正常换源、安装依赖 然后添加Docker 的官方 GPG 密钥时出错: $ curl -fsSL https://mirrors.ustc.edu.cn/docker-ce/linux/debian/gpg | sudo apt-key add - 提示 bash: sudo: command not …...

springboot的缓存和redis缓存,入门级别教程
一、springboot(如果没有配置)默认使用的是jvm缓存 1、Spring框架支持向应用程序透明地添加缓存。抽象的核心是将缓存应用于方法,从而根据缓存中可用的信息减少执行次数。缓存逻辑是透明地应用的,对调用者没有任何干扰。只要使用…...
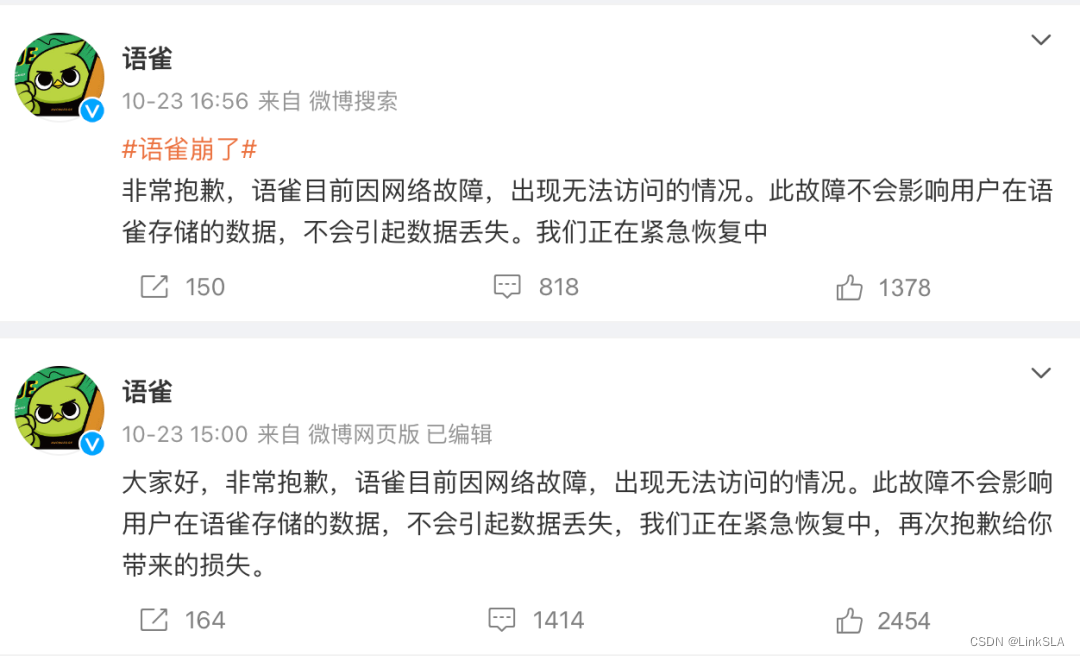
语雀P0级时间爆发,留给运维的时间不多了?
事件背景 打工人的焦虑,已经延伸到在线文档了。近日,语雀P0级故障想必大家都有所体会,宕机近8小时,笔记、离线同步完全不可用。作为用户尤其担心我的文档资料是否会因此消失。 这泼天的8小时,放眼互联网界也是相当炸裂…...
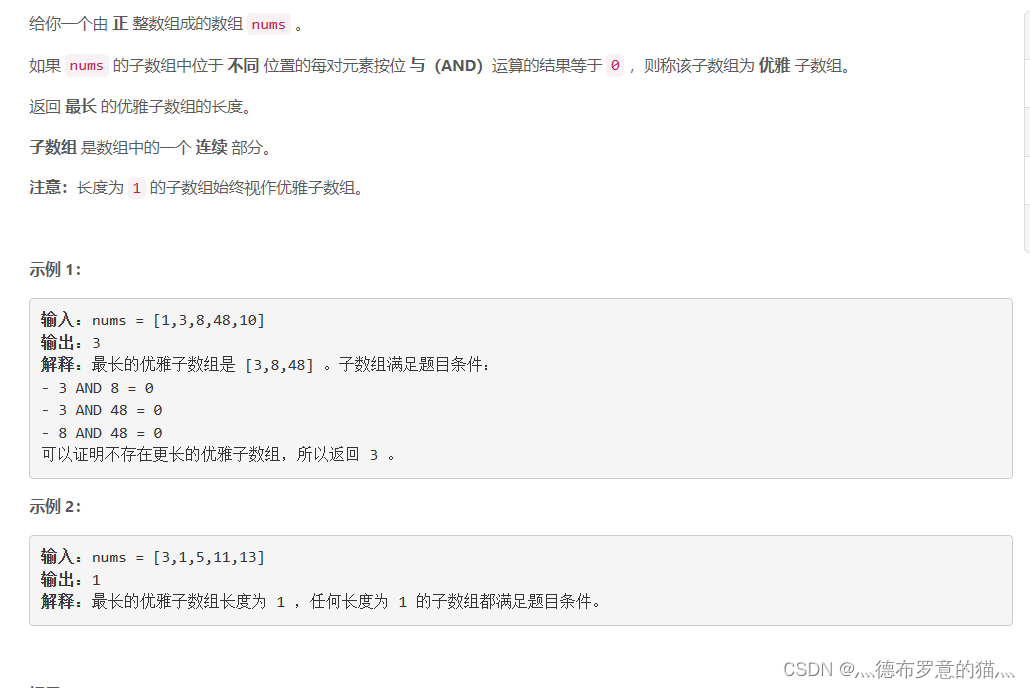
LeetCode 2401.最长优雅子数组 ----双指针+位运算
数据范围1e5 考虑nlog 或者n的解法,考虑双指针 因为这里要求的是一段连续的数组 想起我们的最长不重复连续子序列 然后结合一下位运算就好了 是一道双指针不错的题目 class Solution { public:int longestNiceSubarray(vector<int>& nums) {int n nums…...

NOIP2023模拟6联测27 无穷括号序列
题目大意 小 C C C有一个括号序列 A A A,其长度为 m m m,且序列元素只包含左右括号。他想生成一个无限长的括号序列 B B B,由于 B B B的长度为正无穷,所以其下标可以为任意整数(可以为负)。为了由 A A A生…...
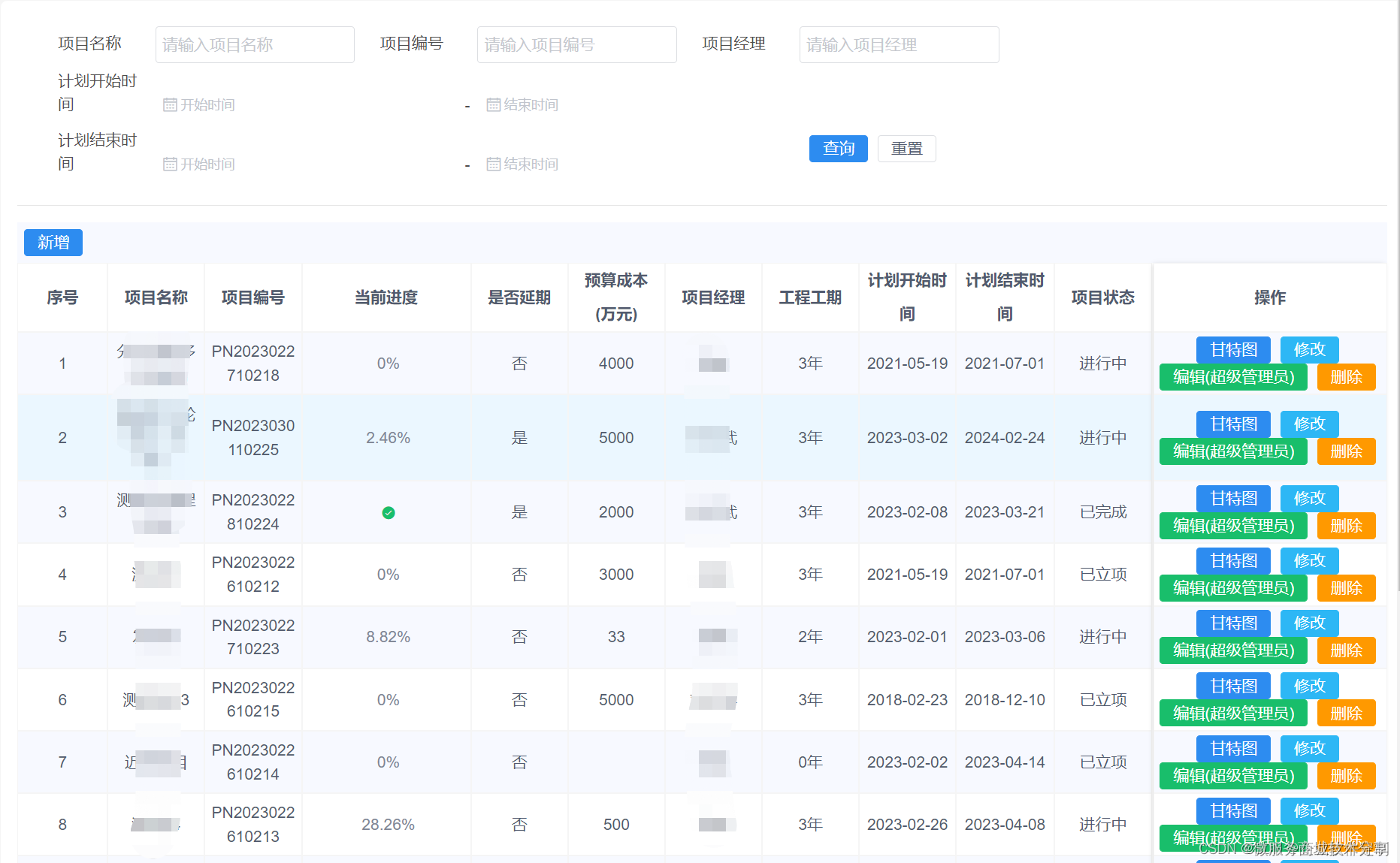
java spring cloud 工程企业管理软件-综合型项目管理软件-工程系统源码
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...
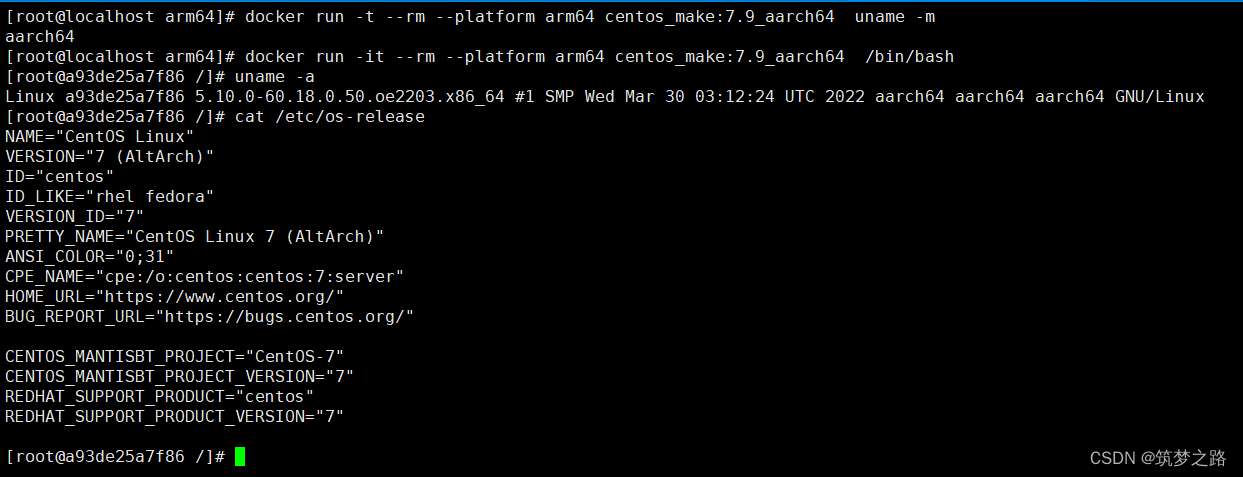
openEuler 22.03 x86架构下docker运行arm等架构的容器——筑梦之路
为什么要这样做? 随着国产化的普及,国家政策对信创产业的支持,尤其一些金融证券行业、政府单位等,逐渐开始走国产化信创的路线,越来越多接触到国产 CPU (arm 平台,比如华为的鲲鹏处理器…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
