2127. 参加会议的最多员工数 : 啥是内向/外向基环树(拓扑排序)
题目描述
这是 LeetCode 上的 「2127. 参加会议的最多员工数」 ,难度为 「困难」。
Tag : 「拓扑排序」、「内向基环树」、「图」
一个公司准备组织一场会议,邀请名单上有 n 位员工。
公司准备了一张圆形的桌子,可以坐下任意数目的员工。
员工编号为 到 。每位员工都有一位喜欢的员工,每位员工当且仅当他被安排在喜欢员工的旁边,他才会参加会议,每位员工喜欢的员工不会是他自己。
给你一个下标从 开始的整数数组 favorite,其中 表示第 位员工喜欢的员工。请你返回参加会议的最多员工数目。
示例 1: 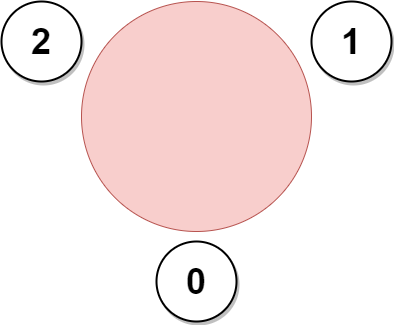
输入:favorite = [2,2,1,2]
输出:3
解释:
上图展示了公司邀请员工 0,1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议,因为员工 2 没办法同时坐在 0,1 和 3 员工的旁边。
注意,公司也可以邀请员工 1,2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。
示例 2:
输入:favorite = [1,2,0]
输出:3
解释:
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示:
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。
示例 3: 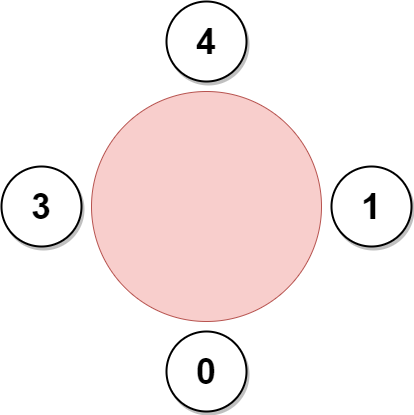
输入:favorite = [3,0,1,4,1]
输出:4
解释:
上图展示了公司可以邀请员工 0,1,3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加,因为他喜欢的员工 0 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。
提示:
内向基环树 + 拓扑排序
根据题意,圆形桌上 左右两边只要有一位是 所喜欢即可。
我们可从 向 添加有向边,从而得到一张包含多个「内向基环树」的图。
内向基环树,是指其满足基环树定义,且内向 bushi。
基环树是指其具有 个点 条边的联通块,而「内向」是指树中任意节点有且只有一条出边,对应的「外向」是指树中任意节点有且只有一条入边。
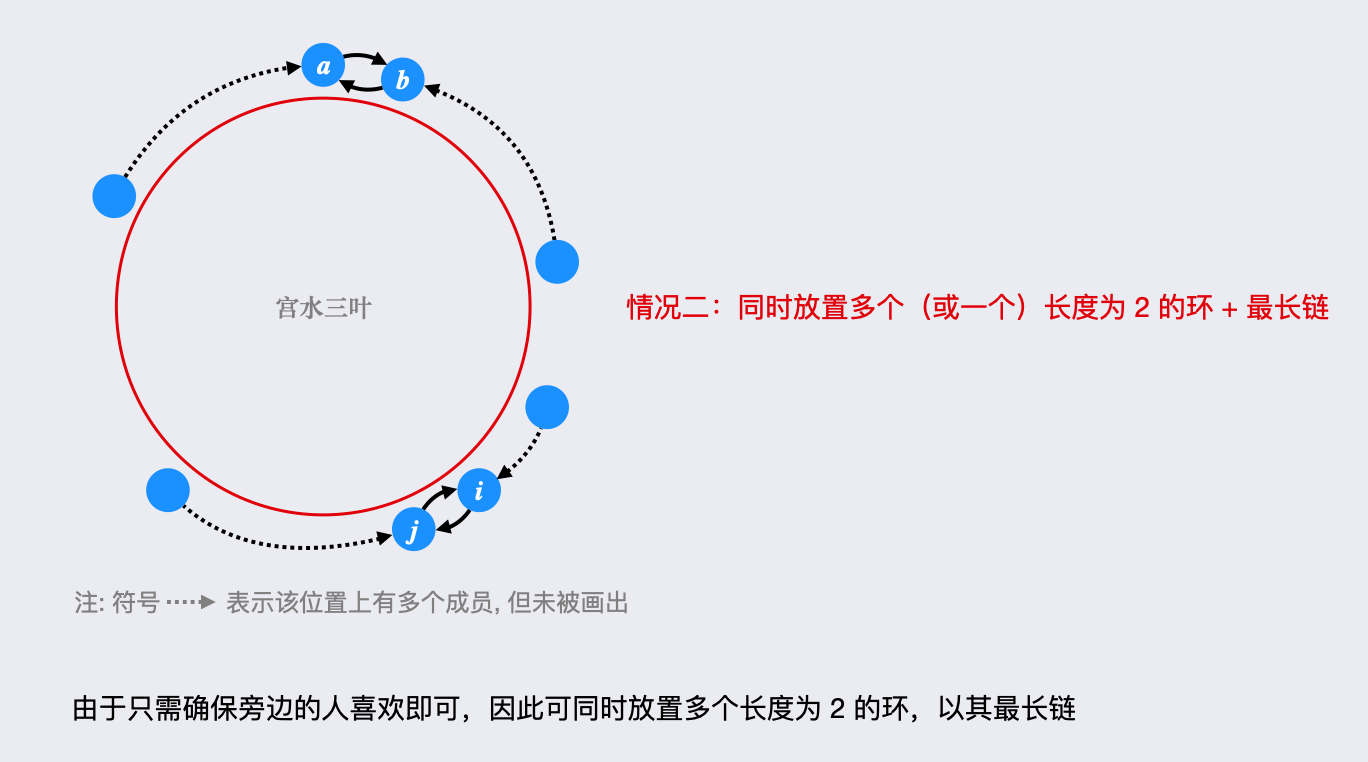
例如,左图内向,右图外向:
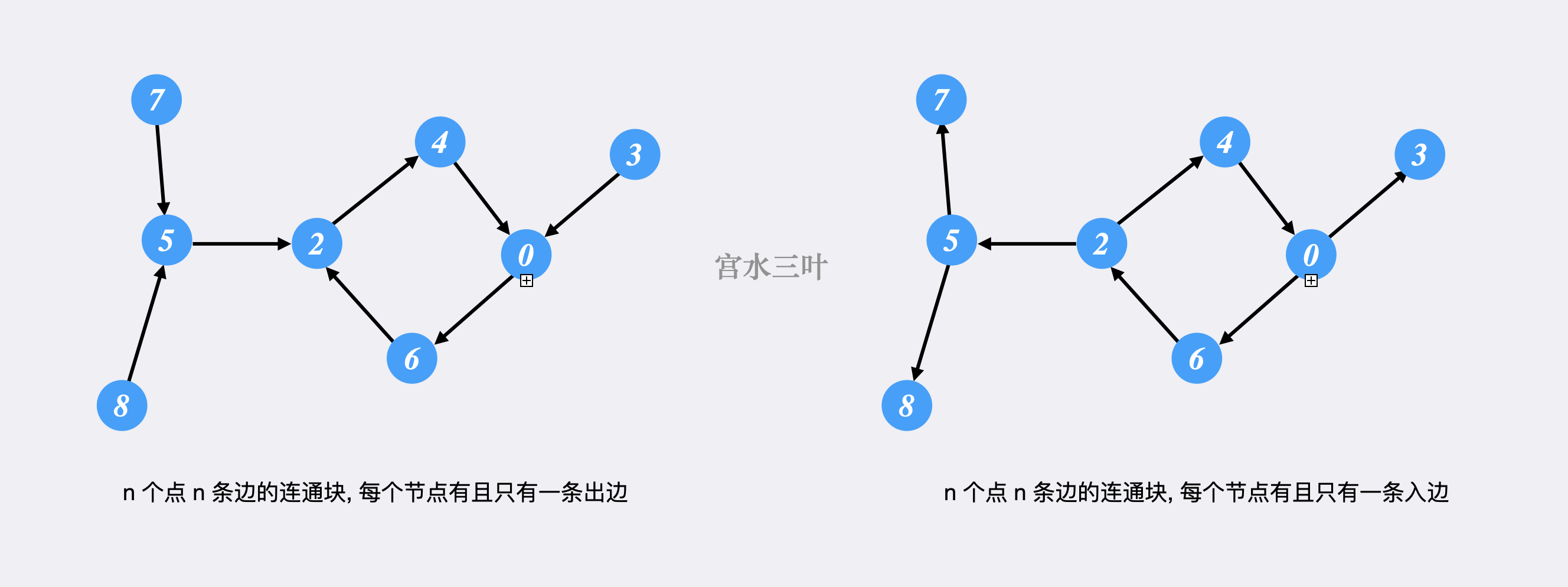
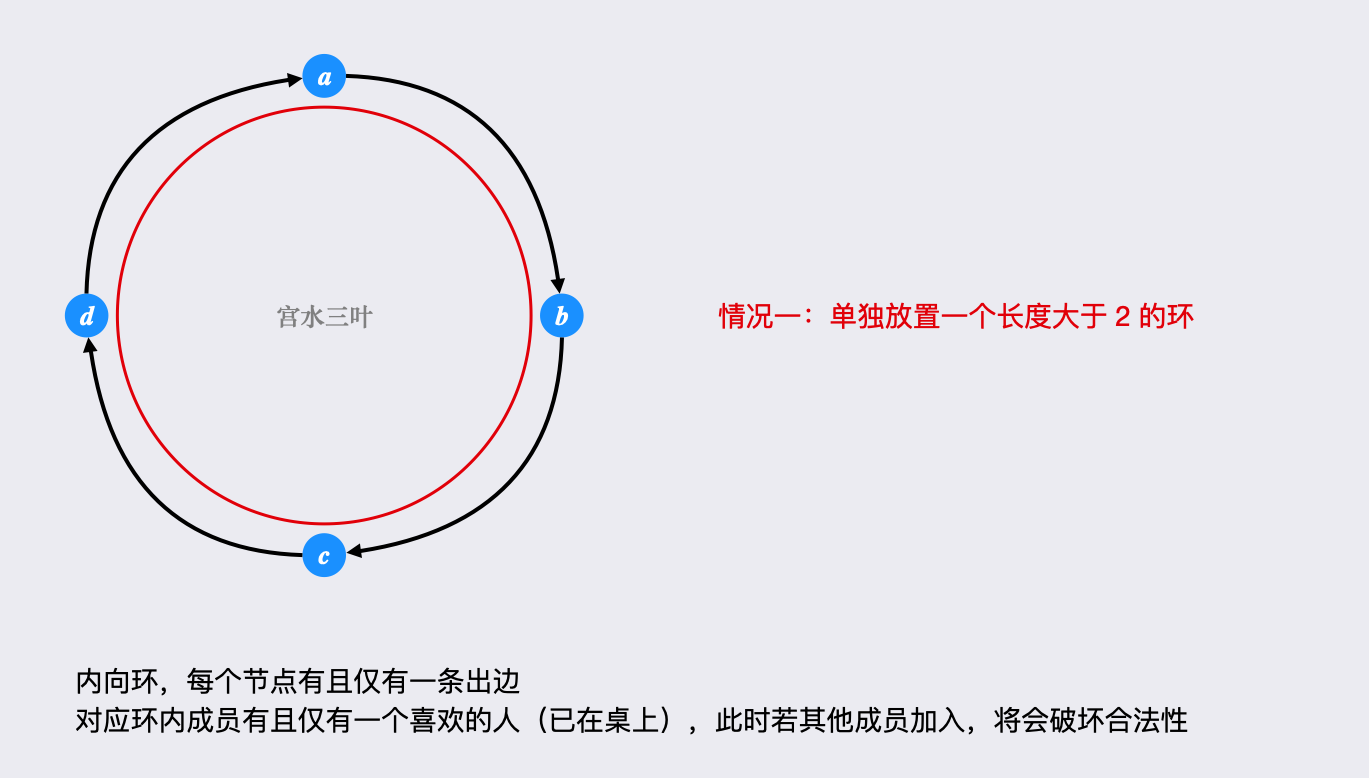
根据题意,「圆桌最多放置一个长度大于 的环(内向环,只有一条出边,即只有一个喜欢的人,安插其他非环成员,会破坏留下参加会议的必要条件),但可放置多个长度为 的环,且多个环可延伸出最长链(利用左右两侧只需有一个喜欢的人即满足)。」
在「取长度大于 的最大环」及「多个长度为 的环及其最长链之和」两者中取最大长度即是答案。
Java 代码:
class Solution {
public int maximumInvitations(int[] favorite) {
int n = favorite.length;
// in 统计每个节点的入度情况, max 统计节最长链
int[] in = new int[n], max = new int[n];
for (int x : favorite) in[x]++;
Deque<Integer> d = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.addLast(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.isEmpty()) {
int cur = d.pollFirst(), ne = favorite[cur];
max[ne] = Math.max(max[ne], max[cur] + 1);
if (--in[ne] == 0) d.addLast(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max[i] + max[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
}
}
Python 代码:
class Solution:
def maximumInvitations(self, favorite: List[int]) -> int:
n = len(favorite)
# in_degree 统计每个节点的入度情况, max_length 统计节最长链
in_degree, max_length = [0] * n, [0] * n
for x in favorite:
in_degree[x] += 1
d = deque()
for i in range(n):
if in_degree[i] == 0:
d.append(i)
# 拓扑排序: 求基环外的最长链
while d:
cur = d.popleft()
ne = favorite[cur]
max_length[ne] = max(max_length[ne], max_length[cur] + 1)
in_degree[ne] -= 1
if in_degree[ne] == 0:
d.append(ne)
# 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
# 圆桌可放置多个等于 2 的环(ans2 累加该长度)
ans1, ans2 = 0, 0
for i in range(n):
if in_degree[i] == 0:
continue
j, cur = favorite[i], 1
while j != i:
# 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0
j = favorite[j]
cur += 1
if cur == 2:
ans2 += 2 + max_length[i] + max_length[favorite[i]]
else:
ans1 = max(ans1, cur)
return max(ans1, ans2)
C++ 代码:
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
int n = favorite.size();
// in 统计每个节点的入度情况, max_length 统计节最长链
vector<int> in(n, 0);
vector<int> max_length(n, 0);
for (int x : favorite) in[x]++;
deque<int> d;
for (int i = 0; i < n; i++) {
if (in[i] == 0) d.push_back(i);
}
// 拓扑排序: 求基环外的最长链
while (!d.empty()) {
int cur = d.front();
d.pop_front();
int ne = favorite[cur];
max_length[ne] = max(max_length[ne], max_length[cur] + 1);
if (--in[ne] == 0) d.push_back(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++) {
if (in[i] == 0) continue;
int j = favorite[i], cur = 1;
while (j != i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = max(ans1, cur);
}
return max(ans1, ans2);
}
};
TypeScript 代码:
function maximumInvitations(favorite: number[]): number {
const n = favorite.length;
// in_degree 统计每个节点的入度情况, max_length 统计节最长链
const in_degree = Array(n).fill(0), max_length = Array(n).fill(0);
for (const x of favorite) in_degree[x]++;
const d = [];
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) d.push(i);
}
// 拓扑排序: 求基环外的最长链
while (d.length > 0) {
const cur = d.shift() as number;
const ne = favorite[cur];
max_length[ne] = Math.max(max_length[ne], max_length[cur] + 1);
if (--in_degree[ne] === 0) d.push(ne);
}
// 圆桌最多放置一个大于 2 的环(ans1 统计最大值)
// 圆桌可放置多个等于 2 的环(ans2 累加该长度)
let ans1 = 0, ans2 = 0;
for (let i = 0; i < n; i++) {
if (in_degree[i] === 0) continue;
let j = favorite[i], cur = 1;
while (j !== i) {
// 一个环只需被处理一次, 这里将环中其他节点入度置 0, 下次遍历到这些点就会被跳过
in_degree[j] = 0;
j = favorite[j];
cur++;
}
if (cur == 2) ans2 += 2 + max_length[i] + max_length[favorite[i]];
else ans1 = Math.max(ans1, cur);
}
return Math.max(ans1, ans2);
};
-
时间复杂度:统计入度的复杂度为 ;拓扑排序求最长链复杂度为 ;计算答案过程中,每个点最多被访问两次(环内节点),复杂度为 。整体复杂度为 -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2217 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:

2127. 参加会议的最多员工数 : 啥是内向/外向基环树(拓扑排序)
题目描述 这是 LeetCode 上的 「2127. 参加会议的最多员工数」 ,难度为 「困难」。 Tag : 「拓扑排序」、「内向基环树」、「图」 一个公司准备组织一场会议,邀请名单上有 n 位员工。 公司准备了一张圆形的桌子,可以坐下任意数目的员工。 员工…...

Qt入门日记1
目录 1.Qt简介和案例 2.第一个Qt程序 3.学会查看帮助文档 4.创建一个按钮 5.对象树简介 6.Qt的坐标系 7. 信号和槽 7.1自定义信号和槽 7.2信号连接信号 7.3拓展 7.4Qt4版本以前的connect 1.Qt简介和案例 Qt是一个跨平台的C图形用户界面应用程序框架(就是一个库吧…...

SpringBoot_第七章(读写分离)
这里列举了三种读写分离实现方案,分别是如下三种 1:MybatisPlus(读写分离) 1.1:首先创建三个数据库1主2从 表名是user表 1.2:代码实例 1:导入pom <!--MybatisPlus的jar 3.0基于jdk8--><depend…...
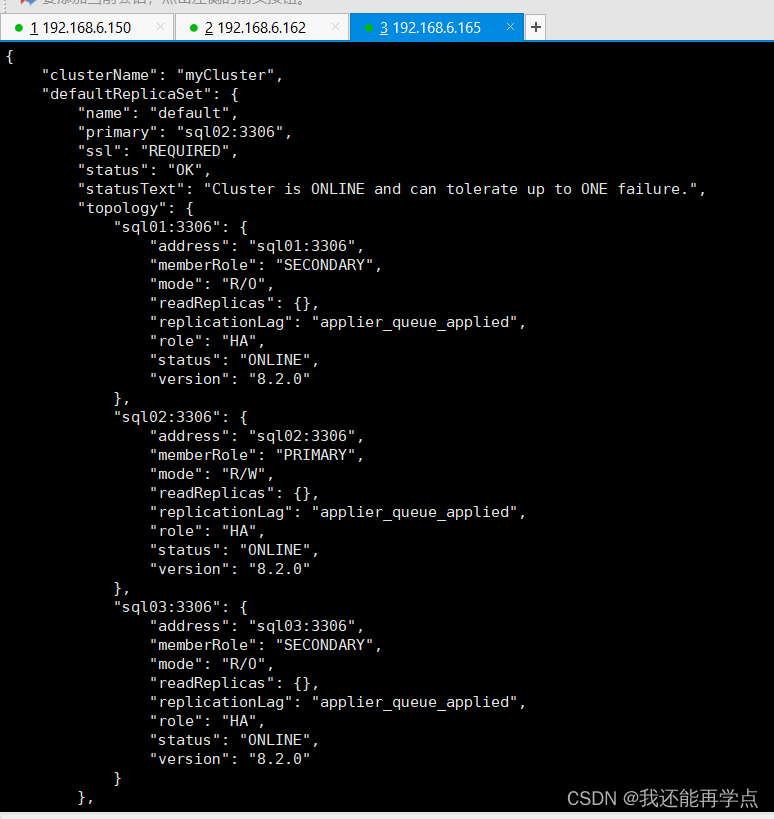
linux下mysql-8.2.0集群部署(python版本要在2.7以上)
目录 一、三台主机准备工作 1、mysql官方下载地址:https://dev.mysql.com/downloads/ 2、修改/etc/hosts 3、关闭防火墙 二、三台主机安装mysql-8.2.0 1、解压 2、下载相应配置 3、初始化mysql,启动myslq,设置开机自启 4、查看初始密…...

40 深度学习(四):卷积神经网络|深度可分离卷积|colab和kaggle的基础使用
文章目录 卷积神经网络为什么要卷积卷积的具体流程池化tensorflow代码 深度可分离卷积原理介绍计算量对比代码参数计算例子 colab 和 kagglecolabkaggle如何在colab上使用kaggle的数据 卷积神经网络 卷积神经网络的基本结构 1: (卷积层(可选)池化层) * N全连接层 *…...

Spring Boot面向切面加注解
一.项目pom.xml文件引入切面依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId> </dependency>二.定义注解类 import java.lang.annotation.*;/*** desc 错误日志注解* au…...

uniapp小程序授权统一处理
1.使用 1.将工具代码引入到utils中 const authorize (scope, isOne false, isMust false) > {if (!scope || !authorizeObj[scope]) {return console.error(请传输需要获取权限的 scope,详见,https://uniapp.dcloud.net.cn/api/other/authorize.html#scope-…...

光学仿真|优化汽车内部照明体验
当我们谈论优化人类感知的内部照明时,我们实际上指的是两个重点领域:安全性和驾驶员体验。如果内部照明可以提供尽可能最佳的体验,驾驶员则能够更好地应对颇具挑战性或意外的驾驶状况,并且减轻疲劳感。除了功能优势外,…...

Spring XML使用CASE WHEN处理SELECT字段
在日常开发中,经常会碰到需要导出的情况。而一些枚举值或者状态一般是定义成整型,这个时候需要对数据进行转换,转换成对应的文本再导出。 在XML中用CASE WHEN来根据不同的查询结果做不同的处理。 比如 SELECT name AS 姓名, age AS 年龄 C…...

关于C#中使用多线程的讨论
关于C#中使用多线程的讨论 C# 中 Thread 调用的函数有返回值 没有输入应该如何解决 如果你想在一个新的线程中调用一个带返回值但没有输入参数的函数,可以使用 Thread 类的委托 ThreadStart 来创建一个新的线程,并在其中调用该函数。然后,你可以使用 Thread 类的 Join 方法…...

工程机械数字孪生可视化平台建设,推动大型装备智能化数字化转型升级
随着信息技术的迅猛发展,数字孪生技术作为一项新兴技术应运而生。数字孪生是指通过数学模型和仿真技术,将实际物理对象与其数字化虚拟模型相互关联,实现对物理对象的全生命周期管理和智能优化。在工程机械领域,巨蟹数科从数字孪生…...
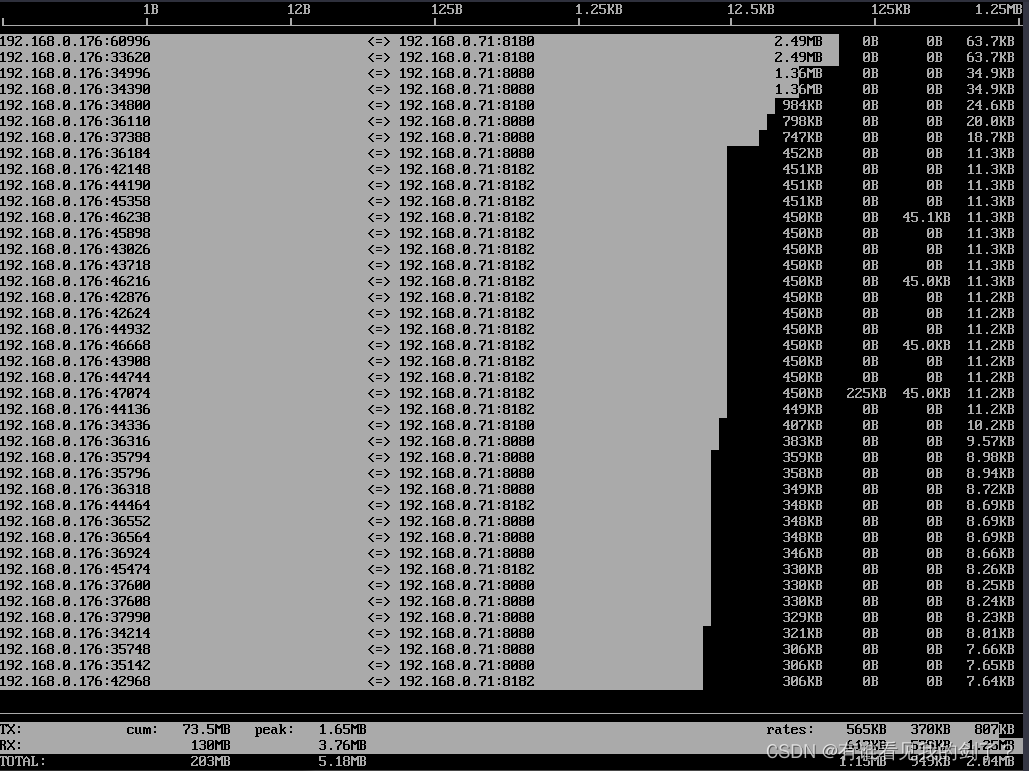
Linux 网络流量监控利器 iftop命令详解及实战
简介 iftop 是什么 在 Linux 系统下即时监控服务器的网络带宽使用情况,有很多工具,比如 iptraf、nethogs 等等,但是推荐使用小巧但功能很强大的 iftop 工具。 iftop 是 Linux 系统一个免费的网卡实时流量监控工具,类似于 top 命令…...
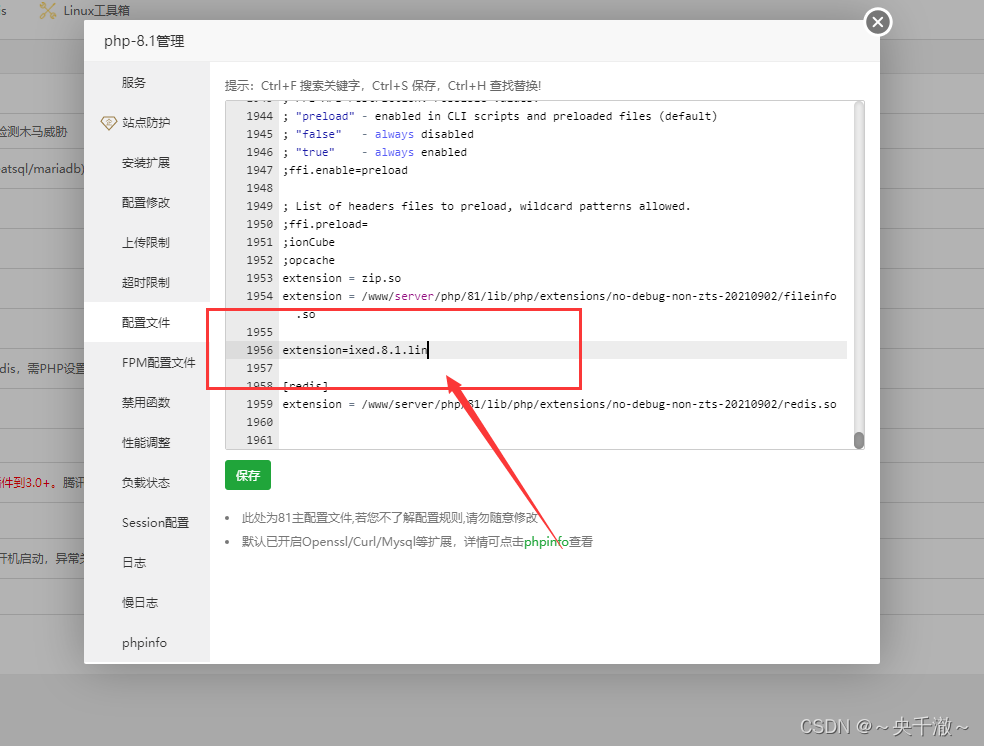
protected by SourceGuardian and requires a SourceGuardian loader ‘ixed.8解决方案
php相关问题 安装程序提示以下内容 遇到某些php程序的安装提示: PHP script ‘/www/wwwroot/zhengban.youyacao.com/install/index.php’ is protected by SourceGuardian and requires a SourceGuardian loader ‘ixed.8.1.lin’ to be installed. 1) Click her…...
)
KWin、libdrm、DRM从上到下全过程 —— drmModeAddFBxxx(14)
接前一篇文章:KWin、libdrm、DRM从上到下全过程 —— drmModeAddFBxxx(13) 上一回讲完了drivers/gpu/drm/drm_framebuffer.c中的framebuffer_check函数中的第一个for循环,本回继续讲解framebuffer_check()接下来的代码。为了便于理解,再次贴出其源码,如下所示: static …...
2023-macOS下安装anaconda,终端自动会出现(base)字样,如何取消
2023-macOS下安装anaconda,终端自动会出现(base)字样,如何取消 安装后,我们再打开终端,就会自动出现了(base) 就会出现这样子的,让人头大, 所以我们要解决它 具体原因是 安装了anac…...
Nginx搭载负载均衡及前端项目部署
目录 编辑 一.Nginx安装 1.安装所需依赖 2.下载并解压Nginx安装包 3.安装nginx 4.启动Nginx服务 二.Tomcat负载均衡 1.准备环境 1.1 准备两个Tomcat 1.2 修改端口号 1.3 配置Nginx服务器集群 2.效果展示 编辑三.前端项目打包 编辑四.前端项目部署 1.上传项目…...

深度学习——炼丹
学习率调整策略 自定义学习率调整策略 简单版 net MyNet()optimoptim.Adam(net.parameters(),lr0.05) for param_group in optim.param_groups: param_group["lr"] param_group["lr"]*0.5print(param_group["lr"]) #0.25复杂版&#…...
Matlab中的app设计
1.窗口焦点问题: 窗口焦点问题:确保你的应用程序窗口正常处于焦点状态。有时,其他窗口的弹出或焦点切换可能导致应用程序最小化。点击应用程序窗口以确保它处于焦点状态。 窗口管理:确保你的 MATLAB 或操作系统没有未处理的错误或…...

曾经遇到过的无法解释的问题
因为不能直接展示生产数据与生产数据结构,所以写一个简单的例子 class Stu{ private String name; private int age; getter setter constructor 略 } List<Stu> list new ArrayList(); list.add(new Stu("s1",16)); list.add(new Stu("…...
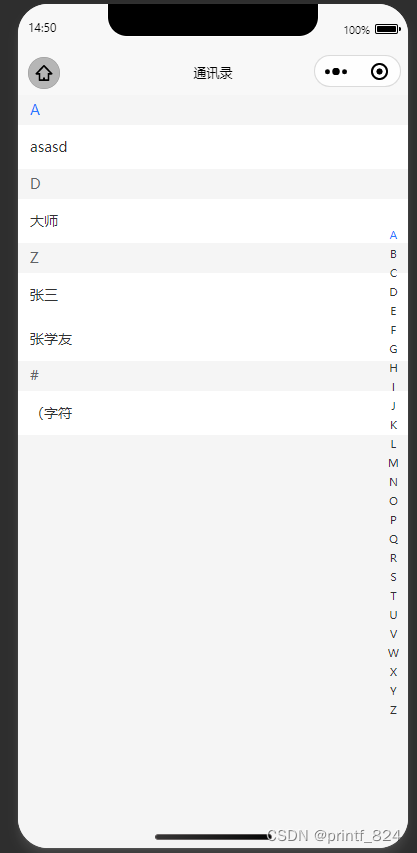
基于uniapp与uview做一个按拼音首字母排序的通讯录页面
效果图: 第一步导入pinyin库并应用,用于区分汉字的拼音首字母 npm i pinyin import pinyin from "pinyin" 完整算法: function getListByPinyinFirstLetter(data) {const newList {};for (const item of data) {let firstLett…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
