CF1265E Beautiful Mirrors
CF1265E Beautiful Mirrors
洛谷CF1265E Beautiful Mirrors
题目大意
Creatnx \text{Creatnx} Creatnx有 n n n面魔镜,每天她会问一面镜子:“我漂亮吗?”,第 i i i面魔镜有 p i 100 \dfrac{p_i}{100} 100pi的概率告诉 Creatnx \text{Creatnx} Creatnx她漂亮。
Creatnx \text{Creatnx} Creatnx从第 1 1 1面镜子开始,每天询问一面镜子。对于第 i i i面镜子,将会发生两种情况:
- 如果这面镜子告诉 Creatnx \text{Creatnx} Creatnx她很漂亮:
- 如果这是第 n n n面镜子,那么 Creatnx \text{Creatnx} Creatnx将会很开心并停止询问
- 否则, Creatnx \text{Creatnx} Creatnx将在第二天询问第 i + 1 i+1 i+1面镜子
- 否则, Creatnx \text{Creatnx} Creatnx将会十分伤心,第二天重新从第 1 1 1面镜子开始询问
求 Creatnx \text{Creatnx} Creatnx停止询问的期望天数对 998244353 998244353 998244353取模后的值。
1 ≤ n ≤ 2 × 1 0 5 , 1 ≤ p i ≤ 100 1\leq n\leq 2\times 10^5,1\leq p_i\leq 100 1≤n≤2×105,1≤pi≤100
题解
令 P i = p i 100 P_i=\dfrac{p_i}{100} Pi=100pi。
设 f i f_i fi表示从第 i i i面镜子开始直到停止询问的期望天数,则转移式如下:
f i = P i × f i + 1 + ( 1 − P i ) × f 1 + 1 f_i=P_i\times f_{i+1}+(1-P_i)\times f_1+1 fi=Pi×fi+1+(1−Pi)×f1+1
也就是说,当前有 P i P_i Pi的可能走到第 i + 1 i+1 i+1面镜子,有 1 − P i 1-P_i 1−Pi的可能走到第 1 1 1面镜子。因为从当前的镜子走到另一面镜子需要花费一天的时间,所以要加 1 1 1。
f n + 1 = 1 f_{n+1}=1 fn+1=1,我们要求的是 f 1 f_1 f1。
但是,每个式子中都有 f 1 f_1 f1,所以我们考虑推式子。
先看 f 1 f_1 f1。
f 1 = P 1 f 2 + ( 1 − P 1 ) f 1 + 1 P 1 f 1 = P 1 f 2 + 1 f 1 = f 2 + 1 P 1 f 2 = f 1 − 1 P 1 f_1=P_1f_2+(1-P_1)f_1+1 \\ \qquad \\ P_1f_1=P_1f_2+1 \\ \qquad \\ f_1=f_2+\dfrac{1}{P_1} \\ \qquad \\ f_2=f_1-\dfrac{1}{P_1} f1=P1f2+(1−P1)f1+1P1f1=P1f2+1f1=f2+P11f2=f1−P11
再看 f 2 f_2 f2。
f 2 = P 2 f 3 + ( 1 − P 2 ) f 1 + 1 f 1 − 1 P 1 = P 2 f 3 + ( 1 − P 2 ) f 1 + 1 P 2 f 1 = P 2 f 3 + 1 P 1 + 1 f 1 = f 3 + 1 P 1 P 2 + 1 P 2 f_2=P_2f_3+(1-P_2)f_1+1 \\ \qquad \\ f_1-\dfrac{1}{P_1}=P_2f_3+(1-P_2)f_1+1 \\ \qquad \\ P_2f_1=P_2f_3+\dfrac{1}{P_1}+1 \\ \qquad \\ f_1=f_3+\dfrac{1}{P_1P_2}+\dfrac{1}{P_2} f2=P2f3+(1−P2)f1+1f1−P11=P2f3+(1−P2)f1+1P2f1=P2f3+P11+1f1=f3+P1P21+P21
我们可以发现, f 1 = f i + 1 + 1 P 1 P 2 ⋯ P i + 1 P 2 P 3 ⋯ P i + ⋯ + 1 P i f_1=f_{i+1}+\dfrac{1}{P_1P_2\cdots P_i}+\dfrac{1}{P_2P_3\cdots P_i}+\cdots+\dfrac{1}{P_i} f1=fi+1+P1P2⋯Pi1+P2P3⋯Pi1+⋯+Pi1,也就是
f 1 = f i + 1 + ∑ j = 1 i ∏ k = j i 1 P k f_1=f_{i+1}+\sum\limits_{j=1}^i\prod\limits_{k=j}^i\dfrac{1}{P_k} f1=fi+1+j=1∑ik=j∏iPk1
我们知道 f n + 1 = 0 f_{n+1}=0 fn+1=0,那么就可以用这个式子来求 f 1 f_1 f1了。
时间复杂度为 O ( n ) O(n) O(n)。
code
#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
int n,p[200005];
long long now=1,ans=0;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&p[i]);}for(int i=n;i>=1;i--){now=now*mi(p[i],mod-2)%mod*100%mod;ans=(ans+now)%mod;}printf("%lld",ans);return 0;
}
相关文章:

CF1265E Beautiful Mirrors
CF1265E Beautiful Mirrors 洛谷CF1265E Beautiful Mirrors 题目大意 Creatnx \text{Creatnx} Creatnx有 n n n面魔镜,每天她会问一面镜子:“我漂亮吗?”,第 i i i面魔镜有 p i 100 \dfrac{p_i}{100} 100pi的概率告诉 Creat…...
软件测试/测试开发丨利用ChatGPT自动生成架构图
点此获取更多相关资料 简介 架构图通过图形化的表达方式,用于呈现系统、软件的结构、组件、关系和交互方式。一个明确的架构图可以更好地辅助业务分析、技术架构分析的工作。架构图的设计是一个有难度的任务,设计者必须要对业务、相关技术栈都非常清晰…...
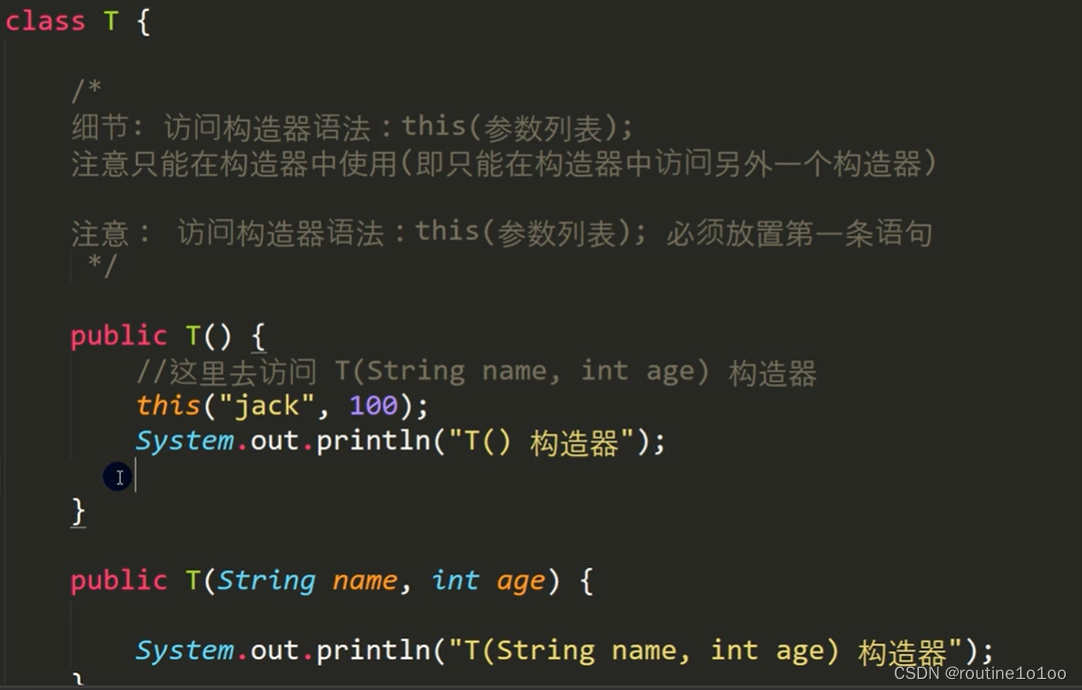
Java学习笔记(六)——面向对象编程(基础)
一、类与对象 (一)类与对象的概念 (二)对象内存布局 编辑 对象分配机制 编辑 (三)属性/成员变量 (四)创建对象与访问属性 二、成员方法 (一)方法…...
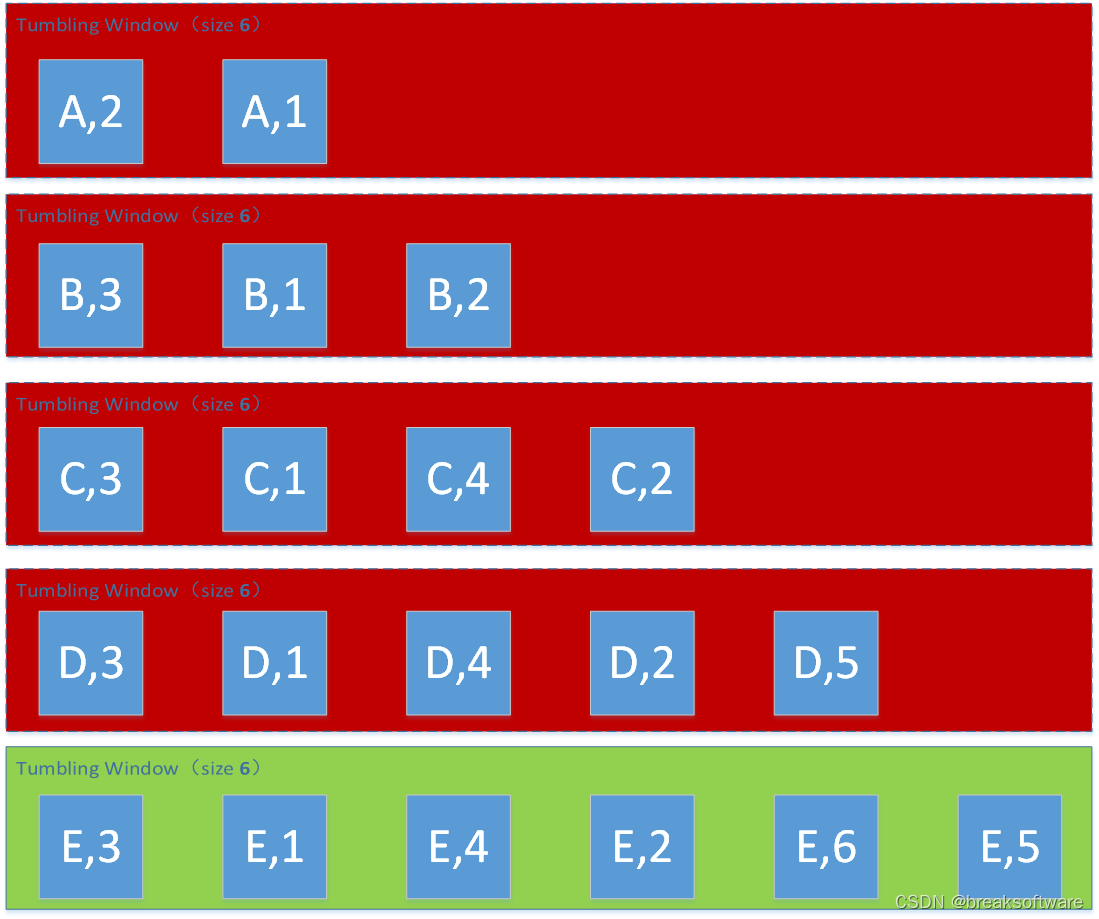
0基础学习PyFlink——个数滚动窗口(Tumbling Count Windows)
大纲 Tumbling Count WindowsmapreduceWindow Size为2Window Size为3Window Size为4Window Size为5Window Size为6 完整代码参考资料 之前的案例中,我们的Source都是确定内容的数据。而Flink是可以处理流式(Streaming)数据的,就是…...

车载终端构筑智慧工厂:无人配送车的高效物流体系
随着科技的不断进步和应用,智能化已经成为许多领域的关键词。在物流行业中,随着无人配送车的兴起和智慧工厂的崛起,车载终端正引领着无人配送车的科技变革之路。 文章同款:https://www.key-iot.com/iotlist/sv900.html 车载终端…...

插件_日期_lunar-calendar公历农历转换
现在存在某需求,需要将公历、农历日期进行相互转换,在此借助lunar-calendar插件完成。 下载 [1] 通过npm安装 npm install lunar-calendar[2]通过文件方式引入 <script type"text/javascript" src"lib/LunarCalendar.min.js">…...

【FreeRTOS】【STM32】08 FreeRTOS 消息队列
简单来说 消息队列是一种数据结构 任务操作队列的基本描述 1.如果队列未满或者允许覆盖入队,FreeRTOS会将任务需要发送的消息添加到队列尾。 2.如果队列满,任务会阻塞(等待)。 3.用户可以指定等待时间。 4.当其它任务从其等待的队列中读取入了数据(这时候队列未满…...
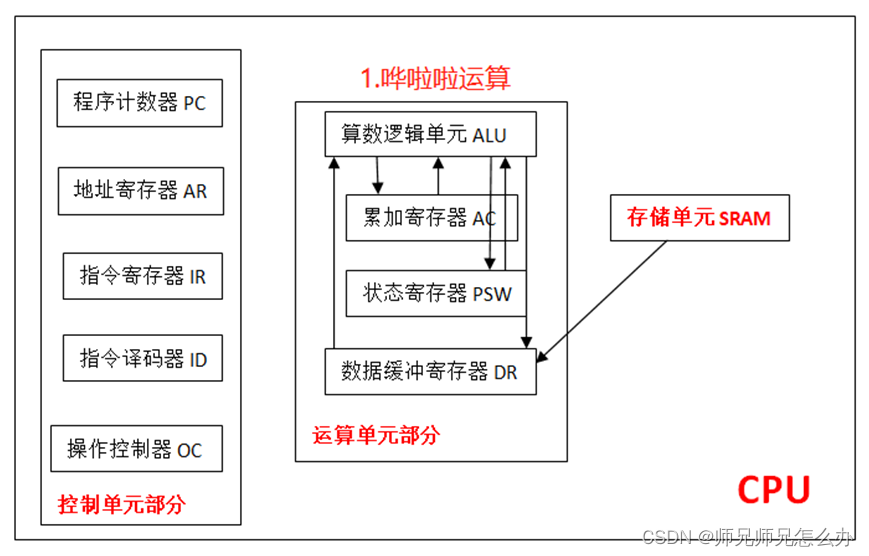
【计算机组成原理】CPU的工作原理
一.CPU的组成结构 CPU主要有运算器、控制器、寄存器和内部总线等组成,其大概的样子长这样: 看不懂没关系,我们将采用自顶而下的方法来讲解CPU的具体工作原理,我们首先来说一下什么叫寄存器,顾名思义,寄存器…...
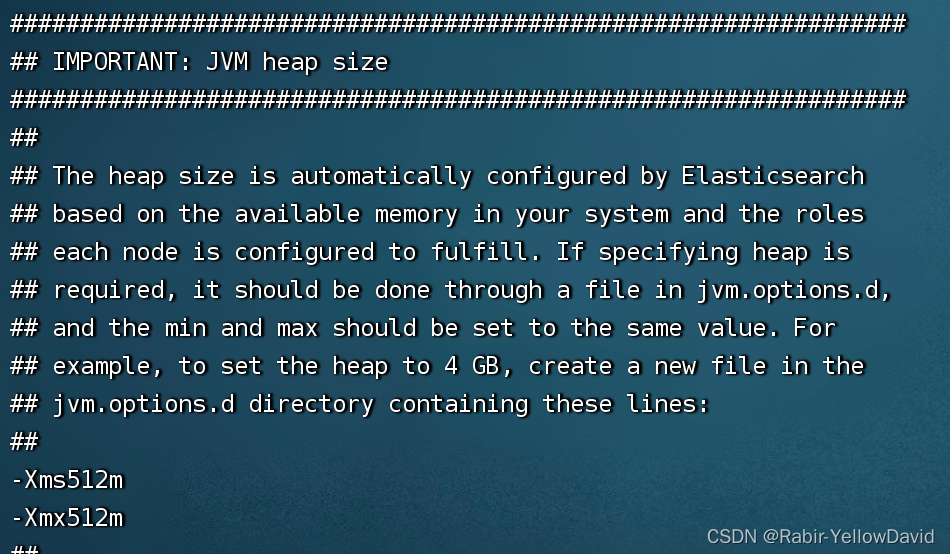
部署ELK
一、elasticsearch #拉取镜像 docker pull elasticsearch:7.12.1 #创建ELK docker网络 docker network create elk #启动ELK docker run -d --name es --net elk -P -e "discovery.typesingle-node" elasticsearch:7.12.1 #拷贝配置文件 docker cp es:/usr/share/el…...

纯前端实现图片验证码
前言 之前业务系统中验证码一直是由后端返回base64与一个验证码的字符串来实现的,想了下,前端其实可以直接canvas实现,减轻服务器压力。 实现 子组件,允许自定义图片尺寸(默认尺寸为100 * 40)与验证码刷新时间(默认时间为60秒)…...

#django基本常识01#
1、manage.py 所有子命令的入口,比如: python3 manage.py runserver 启动服务 python3 manage.py startapp 创建应用 python3 manage.py migrate 数据库迁移 直接执行python3 manage.py 可显示所有子命令...

什么是物流RPA?物流RPA解决什么问题?物流RPA实施难点在哪里?
RPA指的是机器人流程自动化,它是一套模拟人类在计算机、平板电脑、移动设备等界面执行任务的软件。通过RPA,可以自动完成重复性、繁琐的工作,提高工作效率和质量,降低人力成本。RPA适用于各种行业和场景,例如财务、人力…...

乐鑫工程部署过程记录
一、获取编译环境 1、下载sdk,ESP-IDF 这里有很多发布版本,当前我选择的是4.4.6,可以选择下载压缩包,也可以git直接clone 2、配置编译环境 我选择的是Linux Ubuntu下部署开发环境 查看入门指南 选择对应的芯片,我…...

to 后接ing形式的情况
look forward to seeing you. (期待着见到你) She admitted to making a mistake. (承认犯了个错误) He is accustomed to working long hours. (习惯于长时间工作)...

我做云原生的那几年
背景介绍 在2020年6月,我加入了一家拥有超过500人的企业。彼时,前端团队人数众多,有二三十名成员。在这样的大团队中,每个人都要寻找自己的独特之处和核心竞争力。否则,你可能会沉没于常规的增删改查工作中࿰…...

@EventListener注解使用说明
在Java的Spring框架中,EventListener注解用于监听和处理应用程序中的各种事件。通过使用EventListener注解,开发人员可以方便地实现事件驱动的编程模型,提高代码的灵活性和可维护性。本文将详细探讨EventListener注解的使用方法和作用&#x…...
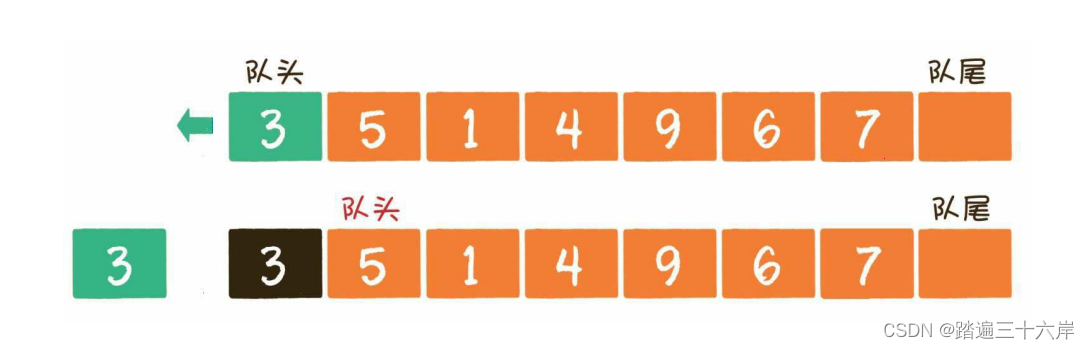
算法通关村第五关-白银挑战实现队列
大纲 队列基础队列的基本概念和基本特征实现队列队列的基本操作Java中的队列 队列基础 队列的基本概念和基本特征 队列的特点是节点的排队次序和出队次序按入队时间先后确定,即先入队者先出队,后入队者后出队,即我们常说的FIFO(first in fi…...

协力共创智能未来:乐鑫 ESP RainMaker 云方案线下研讨会圆满落幕
近日,乐鑫 ESP RainMaker 云方案线下研讨会(深圳)在亚马逊云科技与合作伙伴嘉宾的支持下成功举办,吸引了众多来自智能家电、照明电工、能源和宠物等行业的品牌客户、方案商和制造商。研讨会围绕如何基于乐鑫 ESP RainMaker 硬件连…...

读取谷歌地球的kml文件中的经纬度坐标
最近我在B站上传了如何获取研究边界的视频,下面分享一个可以读取kml中经纬度的matlab函数,如此一来就可以获取任意区域的经纬度坐标了。 1.谷歌地球中划分区域 2.matlab读取kml文件 function [sname,lon,lat] kml2xy(ip_kml) % ip_kml ocean_distubu…...
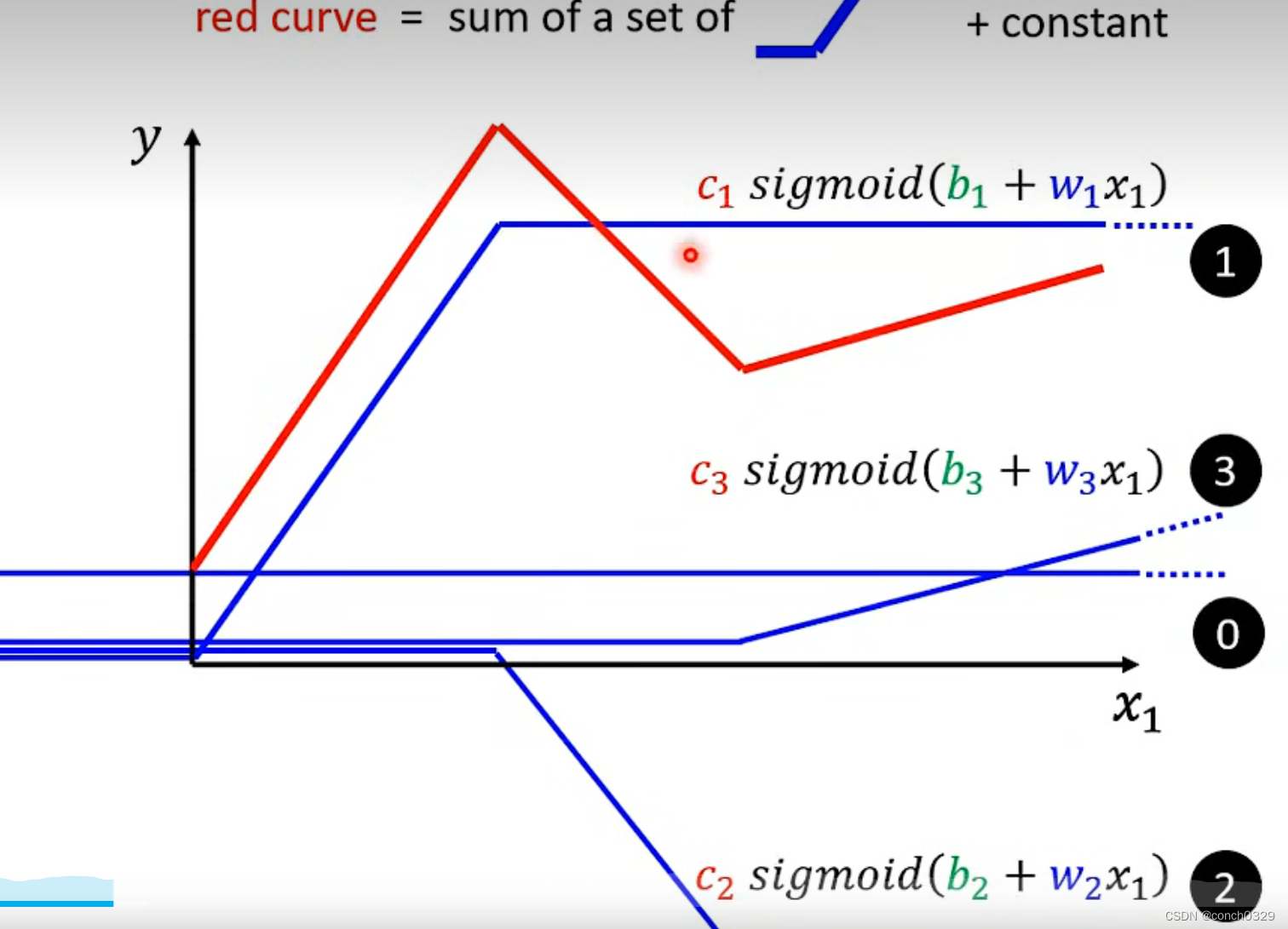
1深度学习李宏毅
目录 机器学习三件事:分类,预测和结构化生成 2、一般会有经常提到什么是标签label,label就是预测值,在机器学习领域的残差就是e和loss编辑3、一些计算loss的方法:编辑编辑 4、可以设置不同的b和w从而控制loss的…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
