剑指 Offer 41. 数据流中的中位数
题目
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,[2,3,4] 的中位数是 3, [2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() -返回目前所有元素的中位数。

思路
优先队列 / 堆
给定一长度为
N的无序数组,其中位数的计算方法:首先对数组执行排序(使用O(NlogN)时间),然后返回中间元素即可(使用O(1)时间)
本题可以根据上述思想,将数据流保存在一个列表中,并在添加元素时保持数组有序,给定一长度为 N 的无序数组,其中位数的计算方法:首先对数组执行排序(使用 O(NlogN) 时间),然后返回中间元素即可(使用 O(1)时间)
借助 堆 进行优化时间复杂度
建立两个堆,一个小顶堆A,一个大顶堆B,各自保存列表的一半元素 ,其中:
- A保存较大的一半,长度为
N/2或者(N+1)/2 - B保存较小的一半,长度为
N/2或者(N+1)/2
最后,中位数可以仅根据A,B的堆顶元素计算得到:

举个例子:数据流 [1,2,3,4,5,6,7,8]
如图所示,则[1,2,3,4]保存在大顶堆B,且堆顶元素为4(因为大顶堆堆顶元素最大),然后[5,6,7,8]保存在小顶堆A,且堆顶元素为5(因为小顶堆堆顶元素最小),这也是为什么大顶堆保存较小的一半,小顶堆保存较大的一半,为了就是可以通过A,B的堆顶元素求中位数
算法流程:
设元素总数为 N = m + n ,其中 m 和 n 分别为 A 和 B 中的元素个数
addNum(num)函数:添加元素,
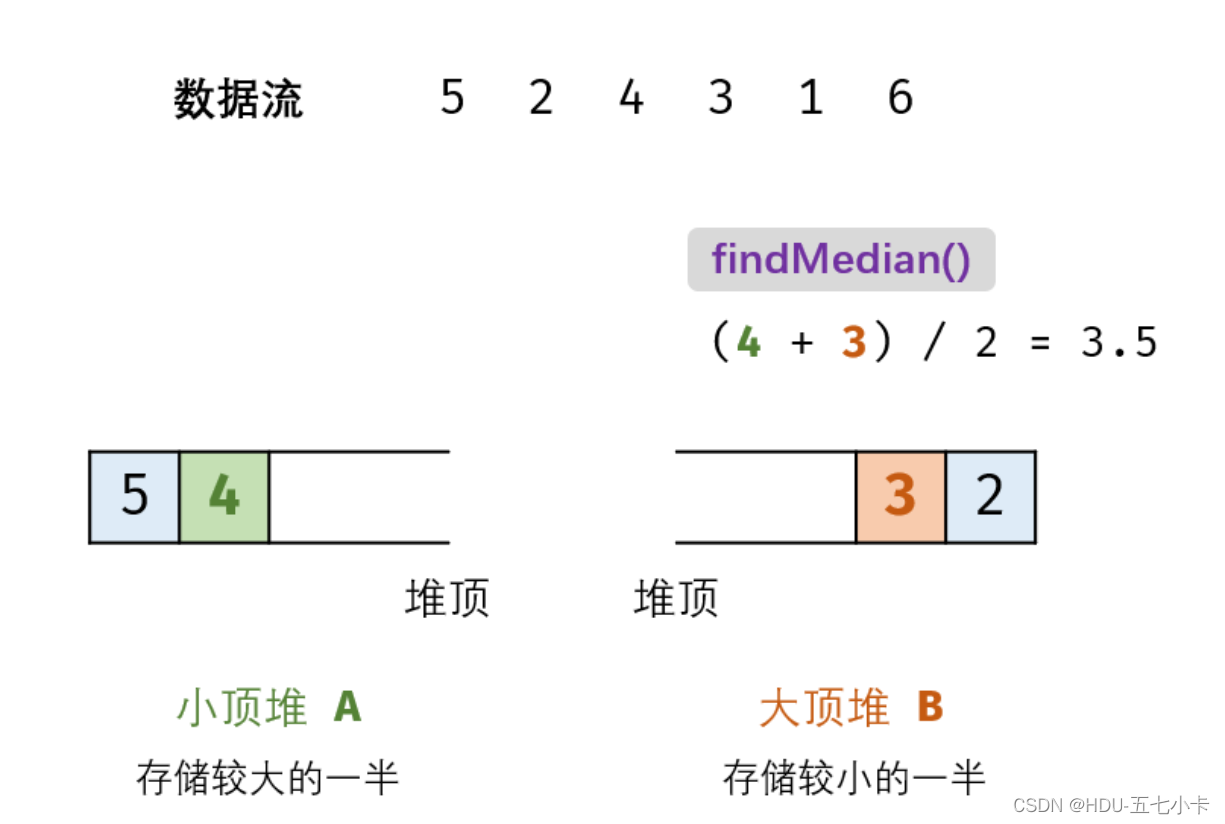
(1)当m=n(即N为 偶数):需向A添加一个元素,即A和B中元素个数相等时,优先往A中先加元素。实现方法:将新元素num插入至B,再将B堆顶元素插入至A(这是为了始终保证A中存较大的一半,B中存较小的一半,因为num可能属于较小的一半,即B中的元素,所以要先加入B,再将B堆顶元素插入A);
举个例子,A中加入1需要先加入B中,然后将B的堆顶元素3加入A
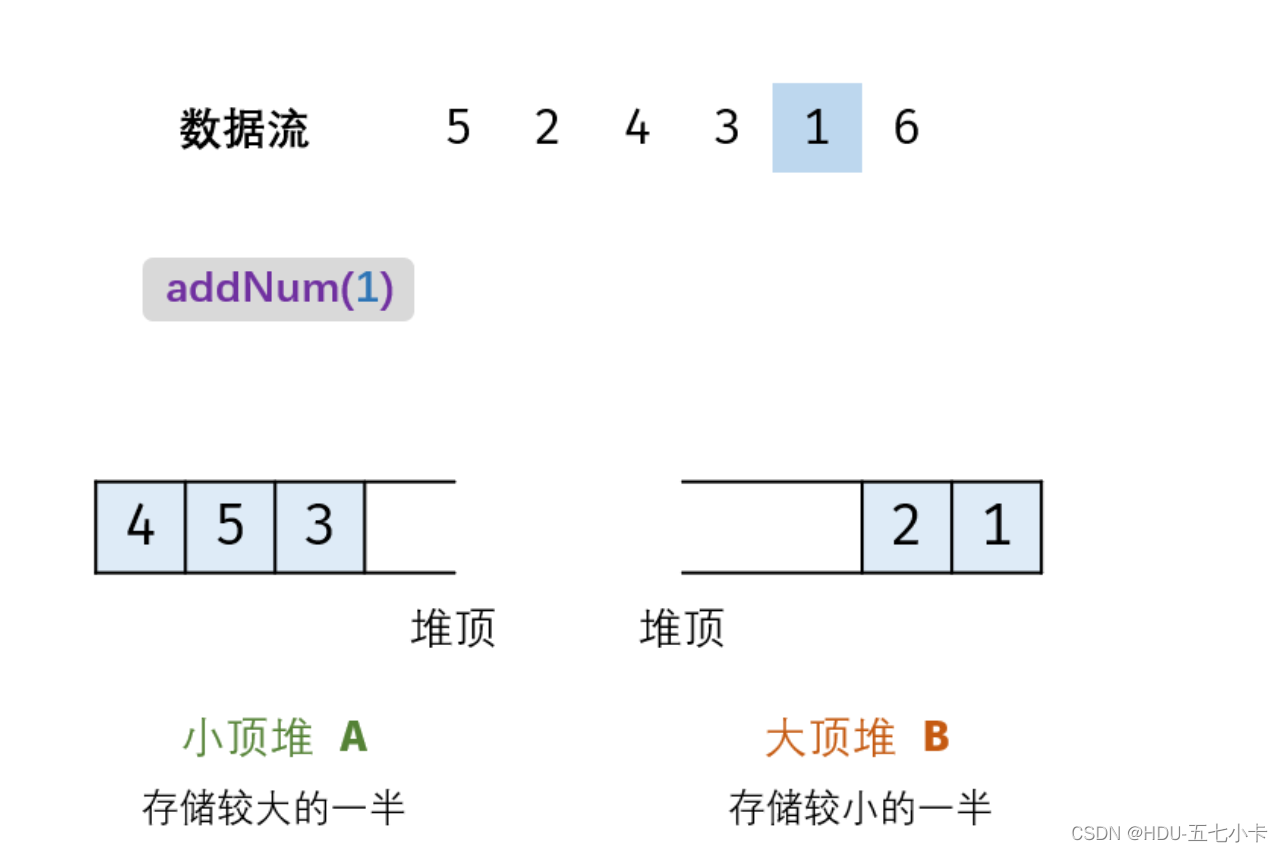
(2)当 m≠n(即 N 为 奇数):需向 B 添加一个元素,此时情况即为A比B多一个元素。实现方法:将新元素 num 插入至 A ,再将A 堆顶元素插入至 B (同理,为了始终保证A中存较大的一半,B中存较小的一半,要先加入A,再将A的堆顶元素插入B,因为num可能属于较大的一般分,即属于A的元素);
举个例子,B中加入6需要先加入A中,然后将A的堆顶元素3加入B
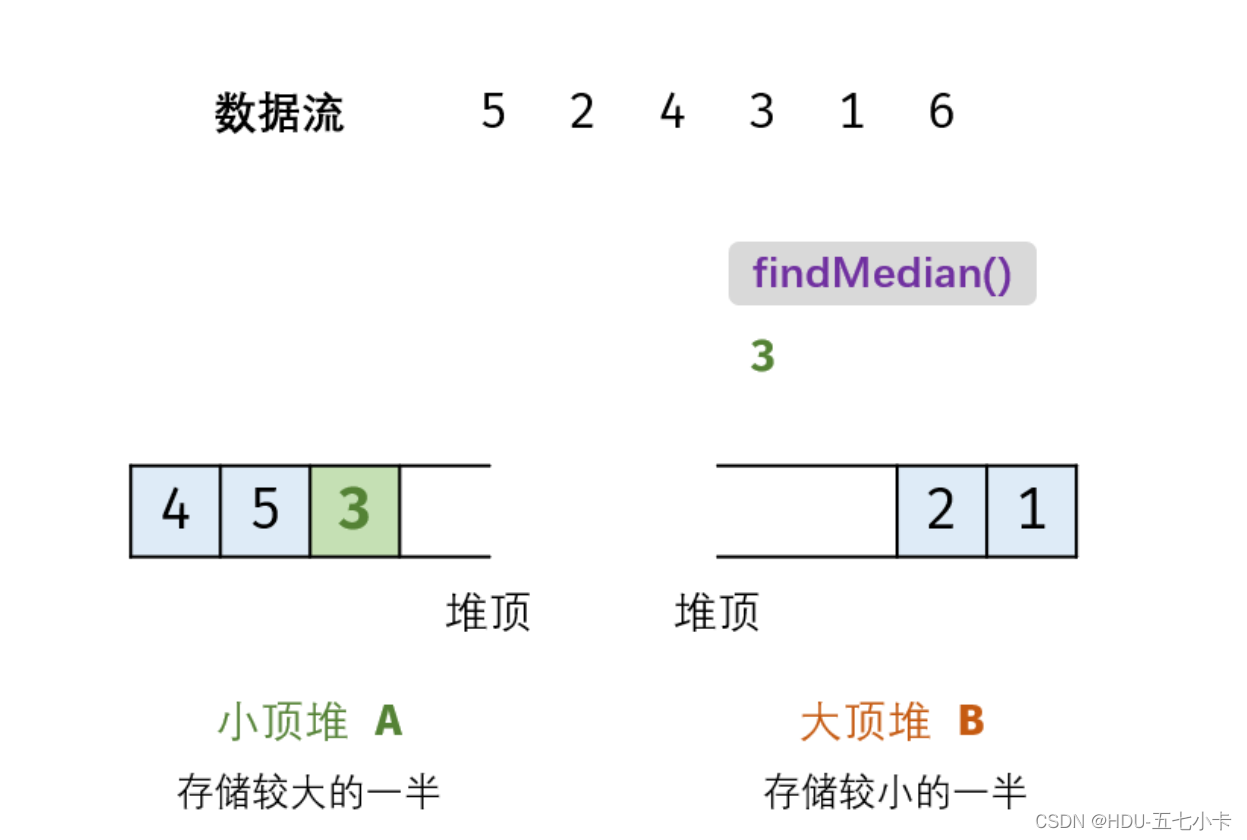

findMedian()函数:找中位数
(1)当m=n(N为 偶数):则中位数为 (A的堆顶元素 +B的堆顶元素 ) / 2
(2)当m≠n(N为 奇数):则中位数为A的堆顶元素。
复杂度分析:
- 时间复杂度:
(1)查找中位数O(1): 获取堆顶元素使用O(1)时间;
(2)添加数字O(logN): 堆的插入和弹出操作使用O(logN)时间 - 空间复杂度
O(N):其中N为数据流中的元素数量,小顶堆A和大顶堆B最多同时保存N个元素。
java代码如下:
class MedianFinder{Queue<Integer> A,B;public MedianFinder() {A = new PriorityQueue<>();//java默认小顶堆,保存较大的一半B = new PriorityQueue<>((x,y) -> (y - x));//使用降序定义大顶堆(因为大顶堆堆顶元素最大,所以是降序,但是用于升序排序,因为每次出堆顶元素是最大的),保存较小的一半}public void addNum(int num){if(A.size() != B.size()){//如果A,B元素个数不相等,则往B中添加元素//但是为了始终保证A中存较大的一半,B中存较小的一半A.add(num);//要先往A中加B.add(A.poll());//然后再将A的堆顶元素加入B} else {//如果A,B元素个数相等,则往A中添加元素//同理为了始终保证A中存较大的一半,B中存较小的一半B.add(num);A.add(B.poll());//要先往B中加//然后再将B的堆顶元素加入A}}public double findMedian(){return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;}
}
相关文章:

剑指 Offer 41. 数据流中的中位数
题目 如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。 例如,[2,3,4] 的中位数是…...

分布式架构下,Session共享有什么方案?
分布式架构下,Session共享有什么方案? 1.不要有Session:但是确实在某些场景下,是可以没有session的,其实在很多借口类系统当中,都提倡【API无状态服务】; 也就是每一次的接口访问,都…...

瀚博半导体载天VA1 加速卡安装过程
背景: 想用 瀚博半导体载天VA1 加速卡 代替 NVIDIA 显卡跑深度学习模型 感谢瀚博的周工帮助解答。 正文: 小心拔出 NVIDIA 显卡,在PCIe 接口插上瀚博半导体载天VA1加速卡,如图: 这时显示屏连接主板的集成显卡 卸载…...

服务降级和熔断机制
🏆今日学习目标: 🍀服务降级和熔断机制 ✅创作者:林在闪闪发光 ⏰预计时间:30分钟 🎉个人主页:林在闪闪发光的个人主页 🍁林在闪闪发光的个人社区,欢迎你的加入: 林在闪闪…...
史上最全最详细的Instagram 欢迎消息引流及示例
史上最全最详细的Instagram 欢迎消息引流及示例!关键词: Instagram 欢迎消息SaleSmartly(ss客服) 寻找 Instagram 欢迎消息示例,您可以用于您的业务。在本文中,我们将介绍Instagram欢迎消息的基础知识和好处…...

MDB 5 UI-KIT Bootstrap 5 最新版放送
顶级开源 UI 套件,Bootstrap v5 和 v4 的材料设计,jQuery 版本,数百个优质组件和模板,所有一致的,有据可查的,可靠的超级简单,1分钟安装简单的主题和定制 受到超过 3,000,000 名开发人员和设计师…...

做专家型服务者,尚博信助力企业数字化转型跑出“加速度” | 爱分析调研
01 从技术应用到业务重构,数字化市场呼唤专家型厂商 企业数字化转型是一个长期且系统性的变革过程。伴随着企业从信息化建设转向业务的数字化重构,市场对数字化厂商的能力要求也在升级。 早期的信息化建设主要是从技术视角切入,采用局部需求…...

CSS 重新认识 !important 肯定有你不知道的
重新认识 !important 影响级联规则 与 animation 和 transition 的关系级联层cascade layer内联样式!important 与权重 !important 与简写属性!important 与自定义变量!important 最佳实践 在开始之前, 先来规范一下文中的用于, 首先看 W3C 中关于 CSS 的一些术语定义吧. 下图…...

android 12添加系统字体并且设置为默认字体
需求:在11.0 12.0系统定制化开发中,在产品定制中,有产品需求对于系统字体风格不太满意,所以想要更换系统的默认字体,对于系统字体的修改也是常有的功能,而系统默认也支持增加字体,所以就来添加楷…...

LeetCode刷题系列 -- 1094. 拼车
车上最初有 capacity 个空座位。车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向)给定整数 capacity 和一个数组 trips , trip[i] [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客,接他们和放他们的…...

二叉查找树的应用 —— K模型和KV模型
文章目录前言1. K模型2. KV模型🍑 构建KV模型的树🍑 英汉词典🍑 统计水果出现的次数3. 总结前言 在上一篇文章中,我们进行了二叉查找树的实现(文章链接),那么今天主要探讨一下二叉查找树的应用…...

深度学习实战(11):使用多层感知器分类器对手写数字进行分类
使用多层感知器分类器对手写数字进行分类 1.简介 1.1 什么是多层感知器(MLP)? MLP 是一种监督机器学习 (ML) 算法,属于前馈人工神经网络 [1] 类。该算法本质上是在数据上进行训练以学习函数。给定一组特征和一个目标变量&#x…...

ThingsBoard-警报
1、使用 IoT 设备警报 ThingsBoard 提供了创建和管理与您的实体相关的警报的能力:设备、资产、客户等。例如,您可以将 ThingsBoard 配置为在温度传感器读数高于某个阈值时自动创建警报。当然,这是一个非常简化的案例,实际场景可能要复杂得多。 2、主要概念 下面让我们回…...
如何去阅读源码,我总结了18条心法
在聊如何去阅读源码之前,先来简单说一下为什么要去阅读源码,大致可分为以下几点原因:最直接的原因,就是面试需要,面试喜欢问源码,读完源码才可以跟面试官battle提升自己的编程水平,学习编程思想…...
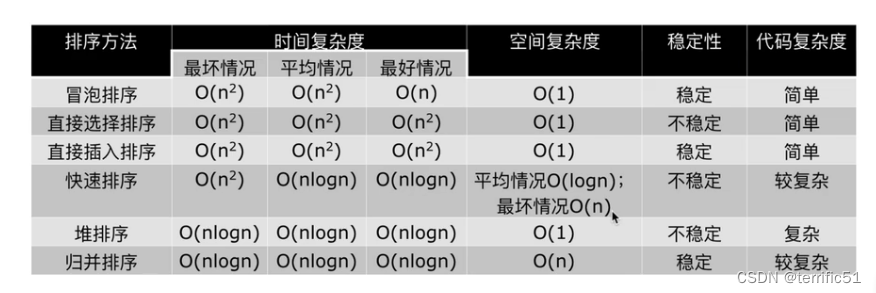
排序:归并排序
一、归并 li[2,4,5,7,//1,3,6,8]#归并的前提是必须两部分排好序 def merge(li,low,mid,high):ilowjmid1ltmp[]while i<mid and j<high: #只要左右两边都有数if li[i]<li[j]:ltmp.append(li[i])i1else:ltmp.append(li[j])j1#while执行完,肯定有一部分没数…...
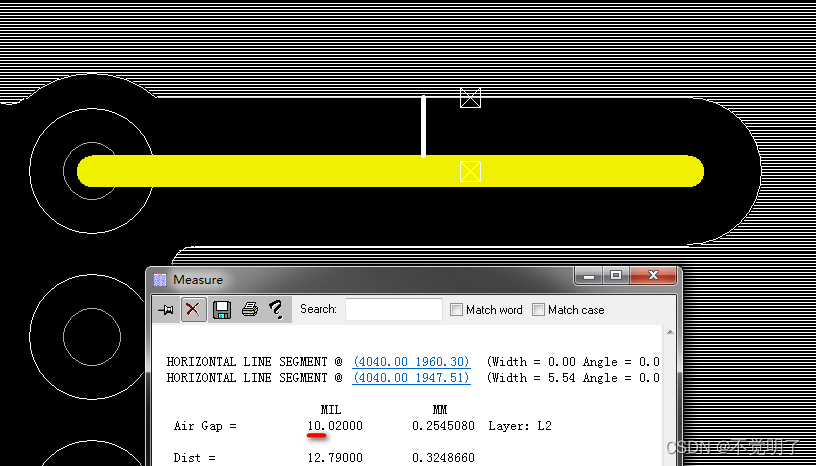
Allegro172版本线到铜皮不按照设定值避让的原因和解决办法
Allegro172版本线到铜皮不按照设定值避让的原因和解决办法 用Allegro做PCB设计的时候,有时会单独给某块铜皮附上线到铜皮额外再增加一个数值,如下图 在规则的基础上,额外再避让10mil 规则避让line到铜皮10.02mil 额外设置多避让10mil,避让的结果却是30.02mil,正确的是20.…...

小白该从哪方面入手学习大数据
大数据本质上是海量数据。 以往的数据开发,需要一定的Java基础和工作经验,门槛高,入门难。 如果零基础入门数据开发行业的小伙伴,可以从Python语言入手。 Python语言简单易懂,适合零基础入门,在编程语言…...
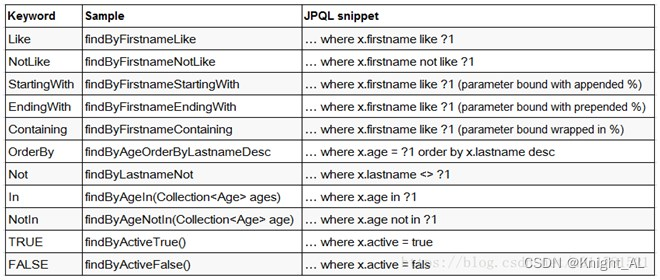
尚医通(十)数据字典加Redis缓存 | MongoDB
目录一、Redis介绍二、数据字典模块添加Redis缓存1、service_cmn模块,添加redis依赖2、service_cmn模块,添加Redis配置类3、在service_cmn模块,配置文件添加redis配置4、通过注解添加redis缓存5、查询数据字典列表添加Redis缓存6、bug&#x…...

为什么我们不再发明编程语言了?
上个世纪,数百种编程语言被发明出来,但是进入21世纪,当我们都进入互联网时代时,只剩那么寥寥几个了。 如果你翻一下TIOBE得编程语言排行榜,就会发现20年来,上蹿下跳的就是那几张老面孔:C , Java…...

预处理指令详解
预处理指令详解**1.预定义符号****2.#define****2.1 #define 定义标识符****2.2 #define 定义宏****2.3 #define 替换规则****2.4 #和##****#的作用****##的作用****2.5 带副作用的宏参数****2.6 宏和函数的对比****宏和函数对比图****2.7 命名约定****3.#undef**4.条件编译4.1…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
