读书笔记——labuladong算法笔记
读书笔记——labuladong算法笔记
- 序言
- 计算机算法世界观
- 计算机算法方法论
- 二叉树遍历
- 广度遍历BFS
- 二叉树的前中后序遍历
- 回溯算法
- 动态规划算法
- 二分搜索算法
- 其他算法
- 滑动窗口
- 双指针
- Union-Find算法
序言
labuladong算法笔记是一本讲解算法题求解技巧的书。本次读书笔记为2023年8月第1版的相关内容,作者为付来东。本书是配套leetcode进行算法讲解的,语言使用C++和Java。本书对于提高算法结题能力的方法是将常用的算法进行抽象,形成系统,以为读者赋能。这个确实是一个很实用的方法论。以下从世界观到方法论,逐渐深入。
计算机算法世界观
什么是计算机算法,计算机算法到底如何求解问题?有三种方法:1、人通过自己的思辨能力,指导计算机算出值,计算机只作为计算器;2、暴力求解,人设计计算机遍历解求值域的方式以及定义解,让计算机进行遍历求解;3、前两者结合。
计算机算法方法论
二叉树遍历
这里的“二叉树”是泛华的概念,指一切在某种状态下需要进入其子状态进行遍历的模式。
广度遍历BFS
广度遍历一般用于求解到根节点的最短距离,这种算法一般空间复杂度比较大,因为需要保存同一层所有“有效节点”。下面展示一下这个算法的解题模板:
template<typename judge_func>
int BFS(node* start, judge_func& target)
{deque<node*> q; // 这个队列包含本次要弹出的节点,以及其子节点q.push_back(start); // 先把起始节点放入unordered_set<node*> visited; // 已经访问过的节点,二叉树不需要,遍历图时需要 int step = 0; // 记录最小步数while (!q.empty()){size_t sz = q.size(); // 记录父亲节点的数量// 依次弹出父亲节点,并将其子节点插入到队列末尾for (int i = 0; i < sz; ++i){node* cur = q.front();q.pop_front();// 判断是不是需要的目标if (target(cur)){return step;}// 如上所述,将当前节点子节点加入队列末尾for (auto sub: cur->subnodes()){if (0 == visited.count(sub)){q.push_back(sub);visited.insert(sub);}}// 更新步数++step;}}
}
过程就是先将第一个节点插入,然后循环判断当前数组中元素数量既是当前节点数量,判断当前节点是不是需要的,如果不是就讲其子节点插入,直到队列中不再有数据为止。
优化:BFS有一种双向BFS优化。因为BFS正向遍历会随着遍历次数增加,遍历的节点数量也会增加,但是如果通过从叶子向根进行遍历加上从叶子向根遍历,那么复杂度将大大降低。
二叉树的前中后序遍历
二叉树遍历其实很简单,主要就是对当前节点的处理时机不同。首先访问当前节点的就是前序,中间访问就是中序,访问完子节点之后再访问的就是后续。框架代码如下:
void traverse(TreeNode* root)
{if (root == nullptr){return; }// 前序位置traverse(root->left);// 中序位置traverse(root->right);// 后序位置
}
回溯算法
这个算法看上去名字很高大上,其实搞某一门学科的人就喜欢把一个简单的说法说的让人觉得“不明觉厉”。所谓回溯算法实际就是“选择->撤销->下一个选择->再撤销…"如此而已。下面给出一个回溯算法的框架伪代码:
result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择(设置下一个选择状态)backtrack(路径, 选择列表)撤销选择(恢复当前选择状态)
回溯算法关心的是到达目标状态的路径情况(重点)。另外,回溯算法和动态规划算法不一样的一点就是,回溯算法没有重叠子问题,没有办法通过字典来进行优化,就是纯的暴力搜索。
动态规划算法
动态规划是各个厂经常考的题目类型,难住过不少工友,当然也包含我。动态规划一般用于求极值。动态规划问题需要满足最优子问题,就是说一个问题的最优解,可以分解成为其子问题的最优解作为参数以后的最优解。子问题之间不能有相关性。动态规划有自顶而下和自底而上两种解法,由于动态规划会存在子问题,因此可以使用备忘录进行加速。解法伪代码如下:
# 自顶而下
def dp(状态1,状态2,状态3,...):for 选择 in 所有可能选择:# 此时的状态可能由于做出的选择而改变result = 求最值(result, dp(状态1,状态2,...))return result# 自底而上
# 初始化base case
dp[0][0][...]=base case
# 进行状态转移
for 状态1 in 状态1的值域:for 状态2 in 状态2的值域:for ...dp[状态1][状态2][...] = 求最值(选择1,选择2,...)
二分搜索算法
二分搜索一般的时间复杂度是O(log(n)),所以看到要求时间是这种形式的很多都是用的二分搜索算法。二分搜索算法原理非常简单,难点在于其边界条件上。所以在写二分算法的时候要先想清楚是要用闭区间还是开区间,另外要明白“中点”这个概念是一个开区间的边界,因为在每次判断必然会判断这个点,因此如果你要用开区间,那么这个点可以直接使用,否则就需要跳过该点。二分搜索框架如下:
int binarySearch(vector<int> nums, int target)
{int left = 0;int right = nums.size() - 1; // 闭区间,因为搜索范围肯定是包含最后一个元素的嘛while (left <= right) // 闭区间两者相等时结束了吗?并没有啊,因为区间中还有一个元素的{int mid = left + (right-left)/2;if (nums[mid] == target){return mid; }else if (nums[mid] < target) // 目标在中点右侧{left = mid + 1; // mid已经验证过所以要+1}else if (nums[mid] > target) // 目标在中点左侧{right = mid - 1;}}return -1;
}
二分搜索还可以扩展为在元素可重复的数组中查找左右边界,框架如下:
int left_bound(vector<int>& nums, int target)
{int left = 0;int right = nums.size(); // 右开区间while (left < right) // 相等时区间内不存在元素,可以跳出{int mid = left + (right-left)/2;if (nums[mid]==target){right = mid; // 重点。相等时移动右边界}else if (nums[mid]<target){left = mid+1;}else if (nums[mid] > target){right = mid; // 开区间,如上所述,中点本身是开区间边界}}return left;
}
上面找到的左边界是闭边界。
其他算法
滑动窗口
滑动窗口一般用于遍历一遍就可以解决数据集子集问题。这种问题在乎的是子集的组合对子集的排列没有严格要求。滑动窗口问题框架如下:
void slidingWindow(string s)
{unordered_map<char,int> window;int left = 0, right = 0;while (left < right && right < s.size()){char c = s[right];window.add(c);right++;// 窗口内数据更新while (left < right && window needs shrink){char d = s[left];window.remove(d);left++;// 窗口数据更新}}
}
双指针
双指针比较灵活,需要注意的就是你可以设计双指针的迭代方式,可以是快慢指针,也可以从起点像两边扩展的指针(对于回文子串有效)。
Union-Find算法
Union-Find算法算是比较奇特的算法了,它用于生成和查找集合中的联合域。生成过程分2步:
1、初始化:每个元素的父节点都是自己;
2、连接:将一个域的父节点的父节点指向另外一个域的父节点;
这样就可以生成一个UF了。代码如下:
class UF
{
private:int count;vector<int> parent;
public:UF(const int& n):count(n),parent(n,0){for (int i = 0; i < n; ++i){parent[i] = i;}}void union(int p, int q){int rootP = find(p);int rootQ = find(q);if (rootP==rootQ)return;parent[rootQ]==rootP;count--;}bool connected(int p, int q){int rootP = find(p);int rootQ = find(q);return rootP==rootQ;}int find(int x){if(parent[x] != x){parent[x] = find(parent[x]);}return parent[x];}int count() const{return count;}
};
相关文章:

读书笔记——labuladong算法笔记
读书笔记——labuladong算法笔记 序言计算机算法世界观计算机算法方法论二叉树遍历广度遍历BFS二叉树的前中后序遍历回溯算法动态规划算法二分搜索算法 其他算法滑动窗口双指针Union-Find算法 序言 labuladong算法笔记是一本讲解算法题求解技巧的书。本次读书笔记为2023年8月第…...

Linux中阶教程:bash shell基础
文章目录 输入输出赋值和计算条件判断函数for 循环数组及其遍历其他控制语句 输入输出 echo表示打印字符串;read表示获取用户输入;$用于引用变量。 # test1.sh bash中用#进行单行注释 echo "input your name:" read user_name echo "h…...

Golang 编译原理
简介 Golang(Go语言)是一种开源的编程语言,由Google开发并于2009年首次发布。它具备高效、可靠的特性,被广泛应用于云计算、分布式系统、网络服务等领域。Golang的编译原理是理解和掌握这门语言的重要基础之一。本文将介绍Golang…...

基于深度学习的动物识别 - 卷积神经网络 机器视觉 图像识别 计算机竞赛
文章目录 0 前言1 背景2 算法原理2.1 动物识别方法概况2.2 常用的网络模型2.2.1 B-CNN2.2.2 SSD 3 SSD动物目标检测流程4 实现效果5 部分相关代码5.1 数据预处理5.2 构建卷积神经网络5.3 tensorflow计算图可视化5.4 网络模型训练5.5 对猫狗图像进行2分类 6 最后 0 前言 &#…...

计算机视觉基础——基于yolov5-face算法的车牌检测
文章目录 车牌检测算法检测实现1.环境布置2.数据处理2.1 CCPD数据集介绍2.1.1 ccpd2019及20202.1.2 文件名字解析 2.2数据集处理2.2.1 CCPD数据处理2.2.2 CPRD数据集处理 2.3 检测算法2.3.1 数据配置car_plate.yaml2.3.2 模型配置2.3.3 train.py2.3.4 训练结果 2.4 部署2.4.1 p…...

【好书推荐】AI时代架构师修炼之道:ChatGPT让架构师插上翅膀
目录 前言 ChatGPT对架构师工作的帮助 快速理解和分析需求 提供代码建议和解决方案 辅助系统设计和优化 提高团队协作效率 如何使用ChatGPT提高架构师工作效率 了解用户需求和分析问题 编码实践和问题解决 系统设计和优化建议 团队协作和沟通效率提升 知识管理和文…...
全局代理和局部代理的区别
在计算机领域中,代理是一种常见的网络技术,它可以帮助用户更好地控制网络访问和数据传输。代理可以分为全局代理和局部代理两种,它们有着不同的作用和适用场景。 一、全局代理 全局代理指的是在系统级别设置的代理,它可以代理所…...
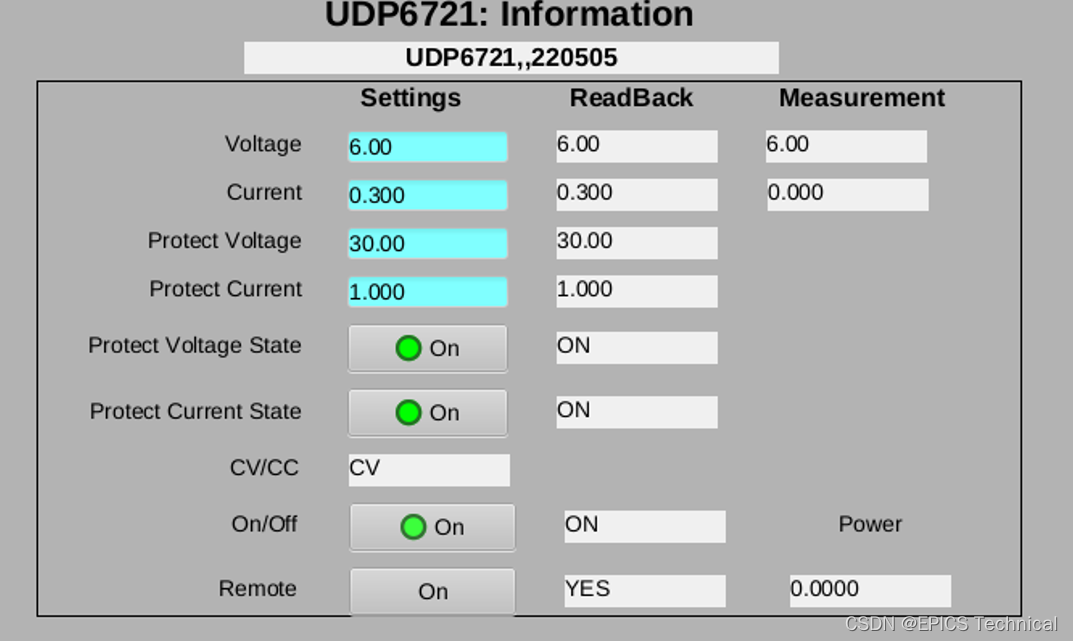
基于EPICS stream模块的直流电源的IOC控制程序实例
本实例程序实现了对优利德UDP6720系列直流电源的网络控制和访问,先在此介绍这个项目中使用的硬件: 1、UDP6721直流电源:受控设备 2、moxa串口服务器5150:将UDP6721直流电源设备串口连接转成网络连接 3、香橙派Zero3:运…...

Unity3D ECS架构适合作为主架构还是局部架构
前言 前言 Unity3D是一款广泛应用于游戏开发的跨平台游戏引擎,提供了丰富的功能和工具来简化游戏开发的过程。而Entity-Component-System(ECS)架构则是一种面向数据的设计模式,它将游戏对象(Entity)分解为…...
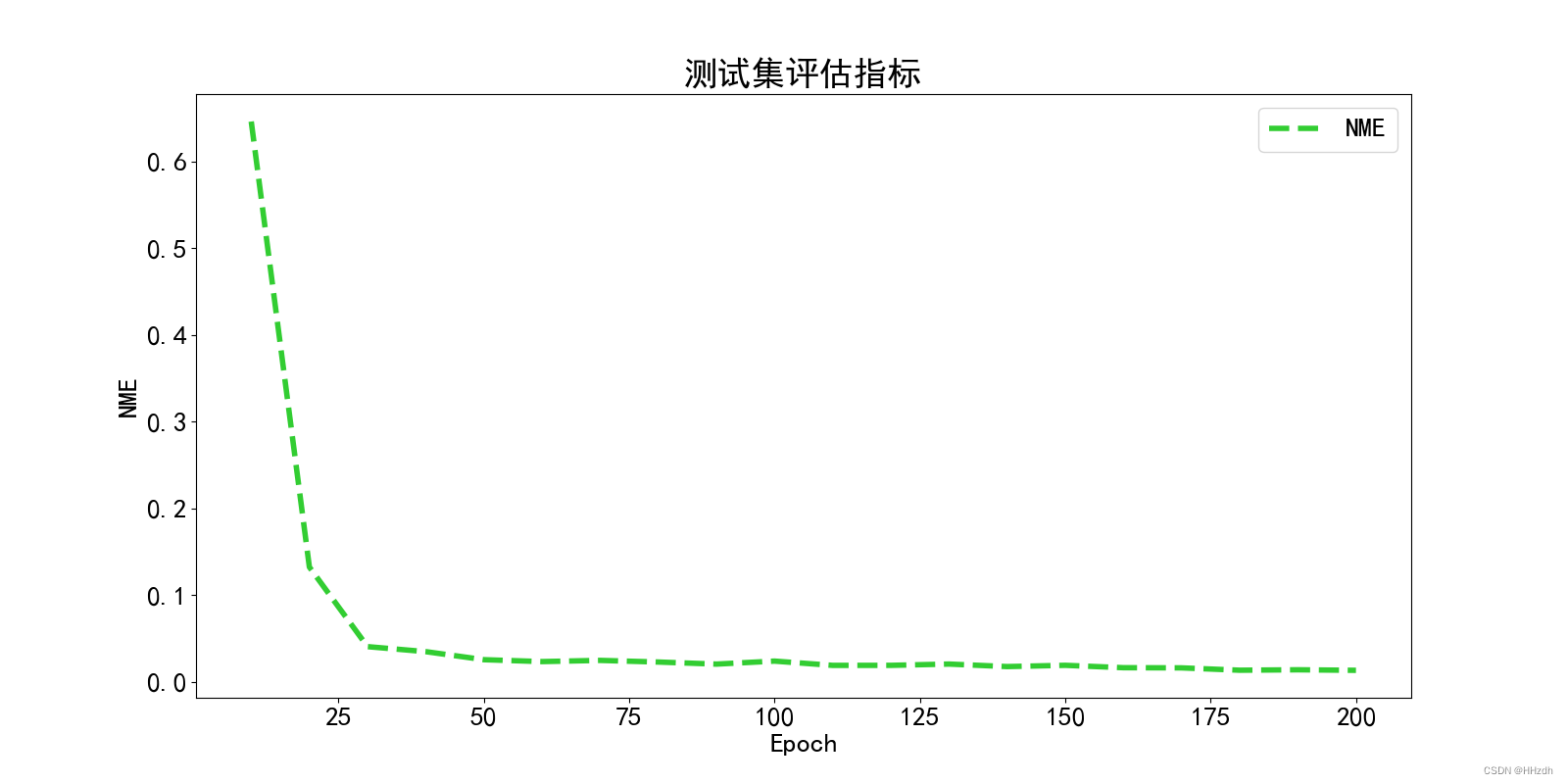
从零开始的目标检测和关键点检测(三):训练一个Glue的RTMPose模型
从零开始的目标检测和关键点检测(三):训练一个Glue的RTMPose模型 一、重写config文件二、开始训练三、ncnn部署 从零开始的目标检测和关键点检测(一):用labelme标注数据集 从零开始的目标检测和关键点检测…...

Qt6 中弹出消息框,一段时间后自动退出
以下代码功能,弹出模态消息框,然后,等待 3 秒,消息框自动退出 QMessageBox msgbox;msgbox.setText("sleep 3s");QTimer::singleShot(3000, &msgbox, &QMessageBox::close);msgbox.exec();...
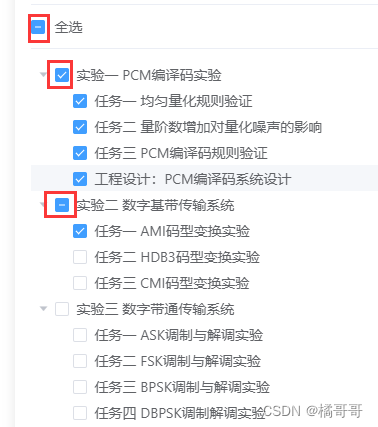
elementUI树节点全选,反选,半选状态
// <template>部分 <div class"check-block"><el-divider></el-divider><el-checkbox :indeterminate"indeterminate" v-model"checkAll" change"handleCheckAllChange">全选</el-checkbox><e…...

Kafka、RabbitMQ、RocketMQ中间件的对比
消息中间件现在有不少,网上很多文章都对其做过对比,在这我对其做进一步总结与整理。 RocketMQ 淘宝内部的交易系统使用了淘宝自主研发的Notify消息中间件,使用Mysql作为消息存储媒介,可完全水平扩容,为了进一步降低成…...

Mac 创建并使用 .zshrc 文件
1,打开终端输入指令 touch .zshrc 2,你可能希望将 .bash_profile 文件中的内容复制到 .zshrc 文件中,那建议复制过来。 3,使用 .zshrc 文件 执行以下指令: source .zshrc 注:以后希望使用 .bash_prof…...

Unity3D移动开发如何依据性能选择Shader
前言 在Unity3D移动开发中,选择合适的Shader是非常重要的,它直接影响到游戏的性能和画面效果。本文将介绍如何依据性能选择Shader,并给出相应的技术详解以及代码实现。 对惹,这里有一个游戏开发交流小组,希望大家可以…...

基于stm32F4的智能宠物喂食器的设计:LVGL界面、定时喂食喂水通风
宠物喂食器 一、功能设计二、元器件选型三、UI设计四、原理图设计五、源代码设计六、成品展示 实物链接:https://m.tb.cn/h.5iCUX6H?tkPL65WXCEipQ CZ3457 一、功能设计 1、设计一个触摸屏作为人机交互 2、通过触摸屏设置时间定时喂食喂水通风 3、获取当前水槽的…...

jumpserver堡垒机docker方式安装部署
1、环境要求 请先自行创建 数据库 和 Redis, 版本要求参考上面环境要求说明 mysql>5.7 redis >5.0 2、创建数据库 mysql: create database jumpserver default charset utf8; GRANT ALL PRIVILEGES ON jumpserver.* TO jumpserver% IDENTIFIED BY nu4x599…...

在基于亚马逊云科技的湖仓一体架构上构建数据血缘的探索和实践
背景介绍 随着大数据技术的进步,企业和组织越来越依赖数据驱动的决策。数据的质量、来源及其流动性因此显得非常关键。数据血缘分析为我们提供了一种追踪数据从起点到终点的方法,有助于理解数据如何被转换和消费,同时对数据治理和合规性起到关…...
VScode clangd 插件浏览 linux 源码
文章目录 VScode clangd 插件浏览 linux 源码clangd 安装与配置VScode 插件安装clangd 安装方法一方法二 clangd 配置 cmake 生成bear 生成 compile_commands.json触发 clangd linux 内核脚本生成 compile_commands.json 文件三种方式对比 VScode clangd 插件浏览 linux 源码 …...
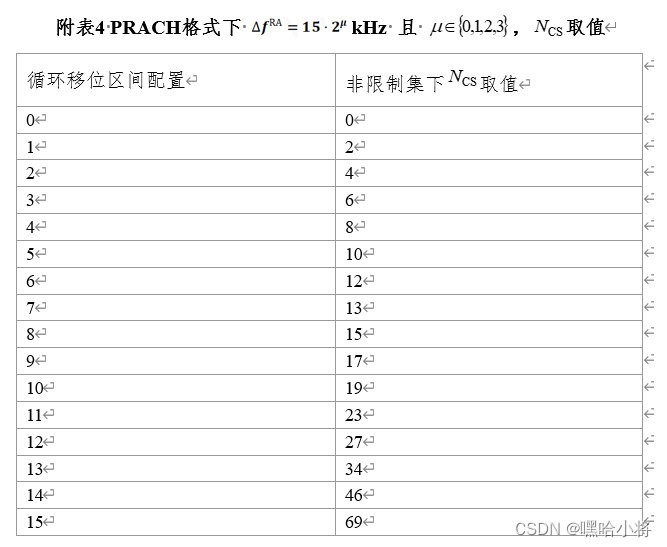
GZ035 5G组网与运维赛题第8套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第8套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
