图论问题建模和floodfill算法
目录
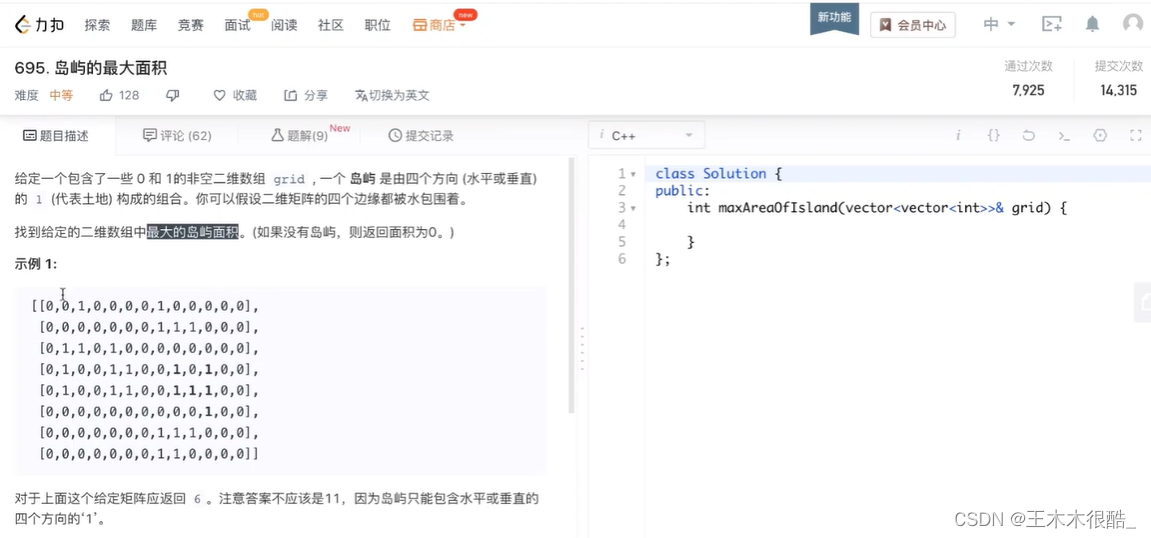
引入:leetcode695.岛屿的最大面积
分析与转换
一维二维转换
四联通
完整代码解答:
1)显示的创建图解决问题的代码
2)不显示的创建图解决此问题的代码
floodfill算法
定义
引入:leetcode695.岛屿的最大面积
分析与转换:
在题目中0是海水,1是陆地。在我们自己设定的图中假设蓝色是海水,红色是陆地。且每一个小格子都是一个顶点,若某个红色顶点上下左右方向有另外的红色顶点与它相邻,则在它俩中间连接一条边证明其一同构成了一个岛屿,也就是同属于一个连通分量。这样,我们就把这道题转换成了一个图论的问题。我们要求的问题也就转换成了找出包含顶点最多的连通分量,顶点个数也就是面积的最大值。

一维二维转换:
我们还可以通过数学公式将二维和一维相互转换。注意一维是从0开始计数, 二维是从1开始计数。

四联通:
我们需要搜索一个红色顶点的上下左右的顶点是否还是陆地,那么如何搜索呢?这就涉及到了四联通的概念。我们可以设立一个二维数组,里面的四个元素代表了相较于本顶点而言,它的行列坐标的位移,也就是表示它的上下左右各移动一个单位的四个坐标。值得注意的是,我们现在的坐标系不是我们熟知的数学坐标系,而是我们计算机一般使用的屏幕坐标系,我们可以理解成二维数组索引所在的坐标系。

d循环四次代表上下左右四个方向。

完整代码解答:
1)显示的创建图解决问题的代码
import java.util.HashSet;class Solution {private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};private int R, C;//行数列数private int[][] grid;private HashSet<Integer>[] G;//图的邻接表的表示private boolean[] visited;public int maxAreaOfIsland(int[][] grid){if(grid == null) return 0;R = grid.length;if(R == 0) return 0;C = grid[0].length;if(C == 0) return 0;this.grid = grid;G = constructGraph();//进行建图操作int res = 0;visited = new boolean[G.length];for(int v = 0; v < G.length; v ++){int x = v / C, y = v % C;if(grid[x][y] == 1 && !visited[v])//如果v没被遍历过就是证明找到了一个新的岛屿,即一个新的连通分量。res = Math.max(res, dfs(v));}return res;}private int dfs(int v){visited[v] = true;int res = 1;//1是这是深度优先遍历v这个顶点for(int w: G[v])if(!visited[w])res += dfs(w);return res;}private HashSet<Integer>[] constructGraph(){HashSet<Integer>[] g = new HashSet[R * C];//开辟空间for(int i = 0; i < g.length; i ++)g[i] = new HashSet<>();for(int v = 0; v < g.length; v ++){int x = v / C, y = v % C;//转换成二维坐标if(grid[x][y] == 1){//只有它本身是陆地才去判断它四周是否有其他陆地与之相连for(int d = 0; d < 4; d ++){int nextx = x + dirs[d][0];int nexty = y + dirs[d][1];if(inArea(nextx, nexty) && grid[nextx][nexty] == 1) {//判断nextx和nexty是否合法(是否在网格范围中)int next = nextx * C + nexty;//转为一维索引g[v].add(next);//添加一条边g[next].add(v);}}}}return g;}private boolean inArea(int x, int y){return x >= 0 && x < R && y >= 0 && y < C;}public static void main(String[] args){int[][] grid = {{0, 1}};System.out.println((new Solution()).maxAreaOfIsland(grid));}
}2)不显示的创建图解决此问题的代码
class Solution {private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};private int R, C;private int[][] grid;private boolean[][] visited;public int maxAreaOfIsland(int[][] grid){if(grid == null) return 0;R = grid.length;if(R == 0) return 0;C = grid[0].length;if(C == 0) return 0;this.grid = grid;visited = new boolean[R][C];int res = 0;for(int i = 0; i < R; i ++)//二重循环遍历每一个顶点for(int j = 0; j < C; j ++)if(grid[i][j] == 1 && !visited[i][j])res = Math.max(res, dfs(i, j));return res;}private int dfs(int x, int y){visited[x][y] = true;int res = 1;for(int d = 0; d < 4; d ++){int nextx = x + dirs[d][0], nexty = y + dirs[d][1];if(inArea(nextx, nexty) && grid[nextx][nexty] == 1 && !visited[nextx][nexty])res += dfs(nextx, nexty);}return res;}private boolean inArea(int x, int y){return x >= 0 && x < R && y >= 0 && y < C;}
}floodfill算法
定义:
floodfill算法是一种图像处理算法,用于填充连通区域。该算法从一个起始点开始,将所有与该点相邻且颜色相同的像素点都标记为同一区域,并继续递归处理该区域的相邻像素点,直到所有相邻像素点都被标记为该区域。该算法通常用于图像处理、计算机图形学等领域中的填充操作,例如对图像中的某个区域进行颜色填充、图形的边界检测等。
相关文章:

图论问题建模和floodfill算法
目录 引入:leetcode695.岛屿的最大面积 分析与转换 一维二维转换 四联通 完整代码解答: 1)显示的创建图解决问题的代码 2)不显示的创建图解决此问题的代码 floodfill算法 定义 引入:leetcode695.岛屿的最大面…...

MySQL - 库的操作
目录 1.库的操作1.1创建数据库1.2创建数据库案例 2.字符集和校验规则3.操纵数据库4.备份和恢复5.查看连接情况 1.库的操作 1.1创建数据库 语法: CREATE DATABASE [IF NOT EXISTS] db_name [create_specification [, create_specification] ...] create_specifica…...

多次kerberos认证服务超时
调整 /var/kerberos/krb5kdc/kdc.conf 文件,有则修改,无则添加 [kdcdefaults] kdc_tcp_listen_backlog 7调整 /etc/krb5.conf [dbmodules] disable_last_success true调整 /etc/sysconfig/krb5kdc KRB5KDC_ARGS‘-w 48’ #增大kdc的进程数量生效上述配…...

Vuex源码-各原理简单总结
1,简单总结 Vuex就是一个构造函数,他拥有install方法和Store类这两个属性。在vue初始化调用new Vue的时候,将store作为参数传入,然后调用Vue.use()实际是调用install方法将store这个实例挂载到全局,从而可以保证全局只…...

vcpkg 使用 cmake 编译C/C++工程代码时指定使用静态库链接编译
参考文献: CMake 项目中的 vcpkg | Microsoft Learn c - Using static Boost libraries with vcpkg and CMake - Stack Overflow Vcpkg updates: Static linking is now available - C Team Blog (microsoft.com) microsoft/vcpkg: C Library Manager for Windo…...

FlinkCDC系列:数据同步对部分字段的处理,只更新部分字段
在flinkCDC源数据配置中,只对表中的部分字段关注,通过监控部分字段进行数据更新或者不更新,对数据进行同步。主要通过以下两个参数: column.exclude.list 默认: 空字符串 一个可选的、以逗号分隔的正则表达式列表,与…...
)
Linux 包操作 (rpm)
目录 1. rpm 包1.1. 提取和安装 rpm 包1.2. 查看一个 rpm 包中的文件安装到那里去 1. rpm 包 rpm --version1.1. 提取和安装 rpm 包 使用以下命令来解压 rpm 包: rpm2cpio package.rpm | cpio -idmv其中, package.rpm 是你要解压的 rpm 包的文件名。这个命令将会将 rpm 包解…...

Docker中OceanBase挂载过后,删除再启动无限重启的解决办法
ob-compose.yml文件如下: version: 3 services:oceanbase1:image: oceanbase/oceanbase-ce:latestcontainer_name: oceanbase1hostname: oceanbase1ports:- 2881:2881restart: alwaysprivileged: truevolumes:#- //d/obdata/ob:/root/ob#- //d/obdata/obd:/root/.o…...

react中的forwardRef 和memo的区别?
文章目录 前言介绍forwardRefmemo适用场景优点缺点后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端面试 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错…...
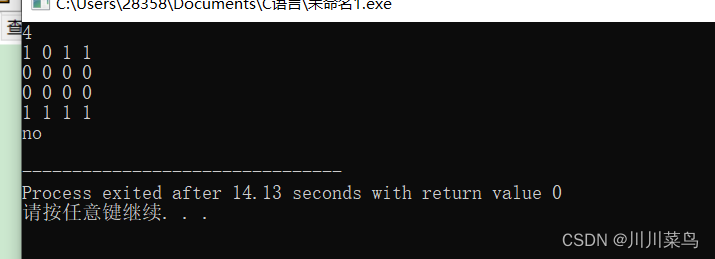
偶数矩阵判断【C语言作业】
题目 若一个布尔矩阵所有行和所有列的和都是偶数,则称为偶数矩阵。请编写一个程序,判断一个布尔矩阵是否是偶数矩阵。 要求: (1)输入:首先输入一个正整数n(n<100),代表该矩阵的大小,接下来是n行n列的矩…...
stable-diffusion 电商领域prompt测评集合
和GhostReivew一个思路,还是从比较好的图片或者是civitai上找一些热门的prompt,从小红书上也找到了不少的prompt,lexica.art上也有不少,主要是为了电商场景的一些测评: 小红书、civitai、Lexica、Liblib.ai、 depth o…...
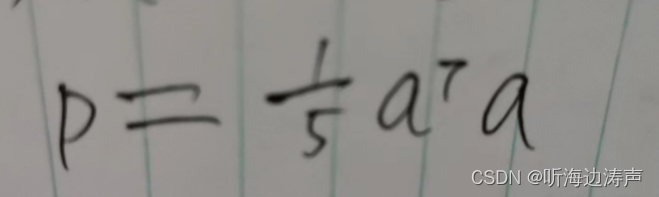
协方差矩阵
将变量两两之间的协方差排成矩阵的形式,就是协方差矩阵。 用个例子来说明下,帮助理解。 下面这组数据有三个变量:身高x、体重y、年龄z,每个变量都有5个取值: 身高x(cm)体重y(kg&a…...
0基础学习VR全景平台篇第117篇:利用插件地拍补地 - PS教程
上课!全体起立~ 大家好,欢迎观看蛙色官方系列全景摄影课程! 嗨,大家好,今天我们来介绍【PS利用插件地拍补地】。 之前已经教给大家补地插件的安装方法,今天我们教给大家如何使用这个插件进行补地。 首…...

git的命令操作
1、基本命令 目录 1、基本命令 创建 Git 存储库 添加文件/目录到索引 将更改提交到本地存储库 撤消上一次提交的更改 显示工作树状态 显示对工作树和索引的更改 显示提交日志 显示提交详细信息 重命名文件 从工作树和索引中移除文件 从工作树中移除未跟踪文件 将…...
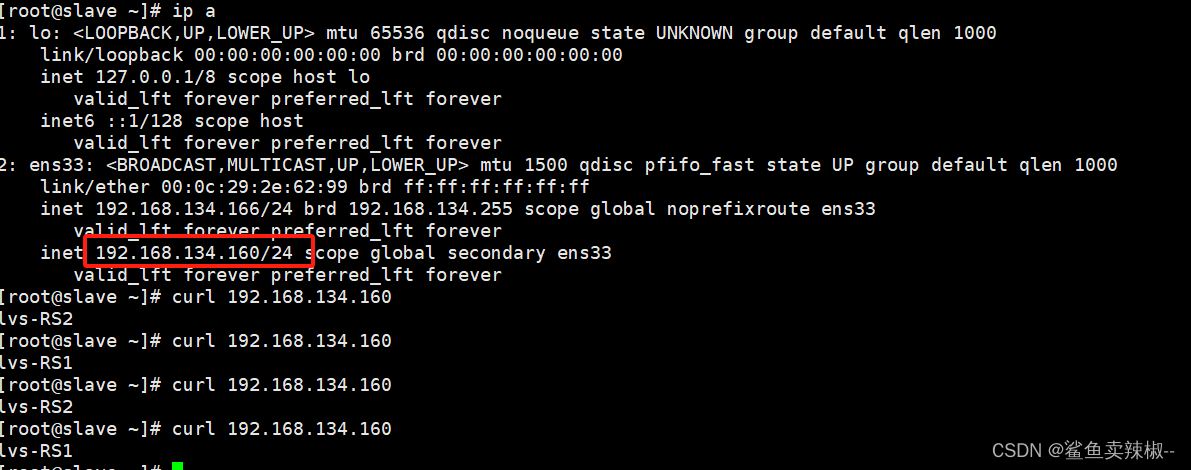
Nginx+keepalived实现七层的负载均衡
1.keepalived VRRP 介绍 keepalived是什么? keepalived是集群管理中保证集群高可用的一个服务软件,用来防止单点故障。 keepalived工作原理 keepalived是以VRRP协议为实现基础的,VRRP全称Virtual Router Redundancy Protocol&…...

至少在两个数组中出现的值
给你三个整数数组 nums1、nums2 和 nums3 ,请你构造并返回一个 元素各不相同的 数组,且由 至少 在 两个 数组中出现的所有值组成。数组中的元素可以按 任意 顺序排列。 示例 1: 输入:nums1 [1,1,3,2], nums2 [2,3], nums3 [3]…...

子女关于骨灰发生争议,骨灰该如何安置?
亲属去世后,争房产、争车辆、争存款的事情不少,但争骨灰却是稀罕事儿。近日,江苏省无锡市梁溪区人民法院审结了一起人格权案件,马某与继母因父亲老马骨灰安葬引发的纷争,历经2年多终于落幕。 老马与前妻离婚后&…...

android隐藏输入法的一些尝试,最后一个可行
一、背景: 基于android开发自己的输入法app,用户需要手动收起输入法 二、准备工作: 定义类 public class CustIMS extends InputMethodService {} 和 xml声明三、尝试验证: 1、CustIMS.hideWindow(); 结论:这个在…...

【go-zero】go-zero 脚手架 simple-admin 第一章:通过goctls生成rpc整个项目 | go-zero整合 ENT数据库orm框架
往期回顾 【simple-admin 开篇:安装 了解 goctls】https://ctraplatform.blog.csdn.net/article/details/133988572 本章内容 往期回顾一、simple-admin 创建rpc项目实战1、创建git仓库1.1、创建任意git仓库1.2、克隆到本地2、创建RPC项目2.1、goctls 安装 rpc项目2.2、复制项…...
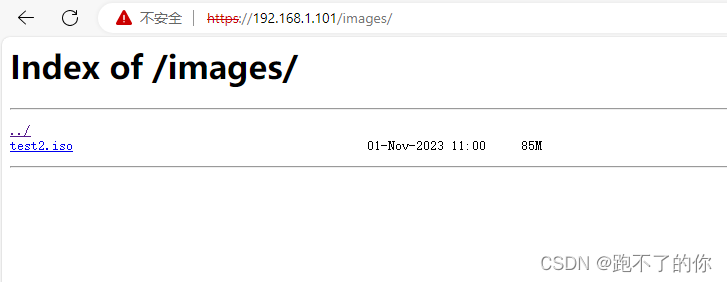
Ubuntu 使用 nginx 搭建 https 文件服务器
Ubuntu 使用 nginx 搭建 https 文件服务器 搭建步骤安装 nginx生成证书修改 config重启 nginx 搭建步骤 安装 nginx生成证书修改 config重启 nginx 安装 nginx apt 安装: sudo apt-get install nginx生成证书 使用 openssl 生成证书: 到对应的路径…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
