二叉树采用二叉链表存储:编写计算整个二叉树高度的算法
二叉树采用二叉链表存储:编写计算整个二叉树高度的算法
(二叉树的高度也叫二叉树的深度)
代码思路:
首先你要明白什么是树的高度,简言之就是树有多少层,如下图:
下面这棵树的高度就是4
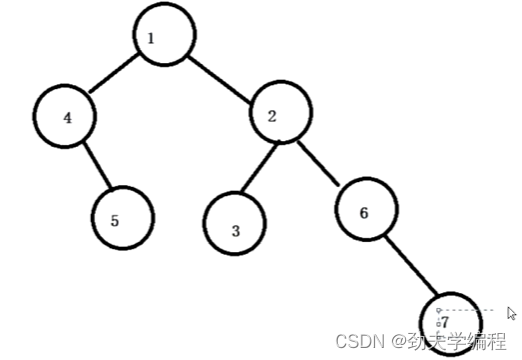
首先我们观察根节点,根节点左子树高度是2,右子树高度是3
那么我们取左右子树高度较大值3,再加上根节点自己一个,那根节点高度就是3+1=4
那么问题来了,我们怎么知道根节点左右子树高度呢?
那就遍历一下根节点左右子树呗,问题转换成求结点左右子树高度,
再然后问题就转换成,求根节点左右子树的子树高度了。。。
这样是不是就是我们熟悉的递归啊。
代码实现如下:
int BiTreeDepth(BiTree T) {if (T != NULL) {//递归退出条件return 0;}int i = 0;//标记左子树高度int j = 0;//标记右子树高度if (T->lchild) {//如果还有左子树,往下递归i = BiTreeDepth(T->lchild);}else {i = 0;}if (T->rchild) {//如果还有右子树,往下递归j = BiTreeDepth(T->rchild);}else {j = 0;}return i >= j ? i+1 : j+1;//向上一层结点返回该子树的深度,注意这里要+1因为还有一个根节点高度
}
相关文章:

二叉树采用二叉链表存储:编写计算整个二叉树高度的算法
二叉树采用二叉链表存储:编写计算整个二叉树高度的算法 (二叉树的高度也叫二叉树的深度) 代码思路: 首先你要明白什么是树的高度,简言之就是树有多少层,如下图: 下面这棵树的高度就是4 首先我们观察根节点࿰…...

antd Cascader级联菜单无法赋值回显问题
说起来太丢人了,自己还拿官网例子在这里调试半天,最后发现是一个特别小儿科的问题哈哈 Cascader级联数据是服务端返回然后自己处理过的,使用了cascader的fileNames属性重置字段名,最后发现服务端回传的数据无法赋值回显在组件上&…...

在react中使用redux react-redux的使用demo
前言: redux是一种状态管理工具,可以存储和操作一些全局或者很多组件需要使用的公共数据。 平心而论,redux的使用对于新上手来说不太友好,多个依赖包的,多种api的结合使用,相对来说比做同样一件事的vuex用起来比较麻烦.不过,熟能生巧,用多了也就习惯了,下面是个人的一个demo,…...

Flutter 06 动画
一、动画基本原理以及Flutter动画简介 1、动画原理: 在任何系统的Ul框架中,动画实现的原理都是相同的,即:在一段时间内,快速地多次改变Ul外观;由于人眼会产生视觉暂留,所以最终看到的就是一个…...
)
优化改进YOLOv5算法之添加MS-Block模块,有效提升目标检测效果(超详细)
目录 前言 1 MS-Block原理 1.1 Multi-Scale Building Block Design 1.2 Heterogeneous Kernel Selection Protocol 2 YOLOv5算法中加入MS-Block...
 for Unoriented Points)
【论文阅读】Iterative Poisson Surface Reconstruction (iPSR) for Unoriented Points
文章目录 声明作者列表核心思想归纳算法流程机器翻译声明 本帖更新中如有问题,望批评指正!如果有人觉得帖子质量差,希望在评论中给出建议,谢谢!作者列表 FEI HOU(侯飞)、CHIYU WANG、WENCHENG WANG:中国科学院大学 HONG QIN CHEN QIAN、YING HE 核心思想归纳 当一条从…...

通过akshare获取股票分钟数据
参考:https://blog.csdn.net/qnloft/article/details/131218295 import akshare as ak 个股的 df ak.stock_zh_a_hist_min_em(symbol“000001”, start_date“2023-11-03 09:30:00”, end_date“2023-11-03 15:00:00”, period‘1’, adjust‘’) print(df) date_info df[‘…...

【论文阅读笔记】Traj-MAE: Masked Autoencoders for Trajectory Prediction
Abstract 通过预测可能的危险,轨迹预测一直是构建可靠的自动驾驶系统的关键任务。一个关键问题是在不发生碰撞的情况下生成一致的轨迹预测。为了克服这一挑战,我们提出了一种有效的用于轨迹预测的掩蔽自编码器(Traj-MAE),它能更好地代表驾驶…...
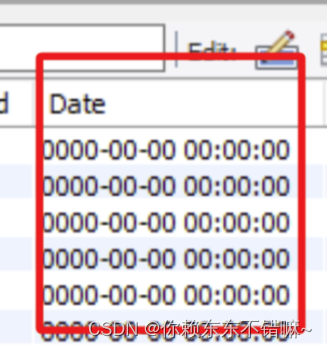
MySQL - Zero date value prohibited
问题: timestamp字段报Caused by: com.mysql.cj.exceptions.DataReadException: Zero date value prohibited 原因: timestamp字段存入了0值, 超出了最小值1900-01-01 00:00:00, 转Java对象的时候报错 解决: 1.修复或删除原数据 2. mysqlurl 中添加zeroDateTimeBehaviorconve…...
+ Spring相关源码)
设计模式——迭代器模式(Iterator Pattern)+ Spring相关源码
文章目录 一、迭代器模式二、例子2.1 菜鸟例子2.1.1 定义迭代器接口2.1.2 定义迭代对象接口——用于返回一个迭代器2.1.3 实现 迭代对象 和 迭代器2.1.4 使用 2.2 JDK源码——ArrayList2.3 Spring源码——DefaultListableBeanFactory 三、其他设计模式 一、迭代器模式 类型&am…...
【word技巧】ABCD选项如何对齐?
使用word文件制作试卷,如何将ABCD选项全部设置对齐?除了一直按空格或者Tab键以外,还有其他方法吗?今天分享如何将ABCD选项对齐。 首先,我们打开【替换和查找】,在查找内容输入空格,然后点击全部…...

如何在uni-app小程序端实现长按复制功能
在开发小程序应用中,常常需要使用到长按复制功能。本文将介绍如何在uni-app小程序端实现长按复制功能。 uni-app是一个跨平台的开发框架,可以基于vue.js语法开发小程序、H5、APP等多个平台的应用。uni-app提供了一些内置组件和API,可以方便地…...

基于springboot实现在线考试平台项目【项目源码+论文说明】计算机毕业设计
基于springboot实现在线考试演示 摘要 网络的广泛应用给生活带来了十分的便利。所以把在线考试管理与现在网络相结合,利用java技术建设在线考试系统,实现在线考试的信息化。则对于进一步提高在线考试管理发展,丰富在线考试管理经验能起到不少…...
【移远QuecPython】EC800M物联网开发板的内置GNSS定位获取(北斗、GPS和GNSS)
【移远QuecPython】EC800M物联网开发板的内置GNSS定位获取(北斗、GPS和GNSS) 测试视频(其中的恶性BUG会在下一篇文章阐述): 【移远QuecPython】EC800M物联网开发板的内置GNSS定位的恶性BUG(目前没有完全的…...

软件设计师2016下半年下午——KMP算法和装饰设计模式
下面是提供的代码的逐行注释,以及对next数组在KMP算法中的作用的解释: #include <iostream> #include <vector> using namespace std;void buildNextArray(const char* pattern, vector<int>& next) {int m strlen(pattern); …...
方法报错)
Android Studio run main()方法报错
在studio中想要测试某个功能直接执行main()方法报错如下: * What went wrong: A problem occurred configuring project :app. > Could not create task :app: **** .main().> SourceSet with name main not found.解决方案: 执行run ** main() w…...

CM3D2 汉化杂记
老物难找资源,于是尝试自己汉化,皆源于有一个好的汉化插件。 资源:LMMT 工具:CM3D2.SubtitleDumper.exe,有道翻译(可以翻译文档),Libreoffice(文档、表格) cmd(资源管理器的结果可以拖进去&…...

分类预测 | Matlab实现SMA-KELM黏菌优化算法优化核极限学习机分类预测
分类预测 | Matlab实现SMA-KELM黏菌优化算法优化核极限学习机分类预测 目录 分类预测 | Matlab实现SMA-KELM黏菌优化算法优化核极限学习机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.MATLAB实现SMA-KELM黏菌优化算法优化核极限学习机分类预测(完整源码和数…...
linux的环境安装以及部署前后端分离后台接口
⭐⭐ linux专栏:linux专栏 ⭐⭐ 个人主页:个人主页 目录 一.linux安装环境 1.1 jdk和tomcat的安装配置 1.1.1 解压jdk和tomcat的安装包 解压jdk安装包 解压tomcat安装包 1.2 jdk环境变量配置 1.3 tomcat启动 1.4 MySQL的安装 二.部署前后端分离…...

解决mysql数据库root用户看不到库
第一种方式: 1.首先停止MySQL服务:service mysqld stop 2.加参数启动mysql:/usr/bin/mysqld_safe --skip-grant-tables & 然后就可以无任何限制的访问mysql了 3.root用户登陆系统:mysql -u root -p mysql 4.切换数据库&#…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
