Seata入门系列【19】分布式事务之CAP、BASE理论
1 CAP理论
CAP是以下三个词语的缩写:
- Consistency:一致性
- Availability:可用性
- Partition tolerance:分区容忍性
CAP理论的基础概念就是在分布式系统中,无法同时满足以上三点。
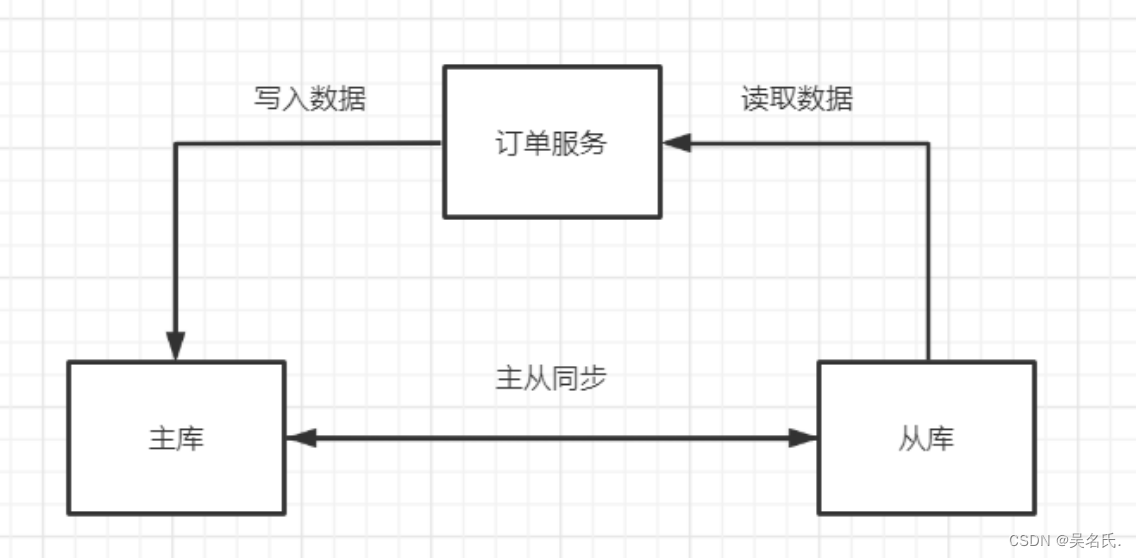
下面我们以一个简单的分布式系统,解释下为何不同通知满足。
2.1 C 一致性
一致性是指写操作后的读操作可以读取到最新的数据状态,当数据分布在多个节点上,从任意结点读取到的数据都是最新的状态。
在上图读写分离的环境中,因为从库同步主库数据是会存在延迟的,必须在写入数据的时候,将从库对应的数据加锁,同步完成后,再释放锁,在等待的过程中,可以返回错误或失败,但要保证客户端读取到的都是最新的数据,从而实现一致性。
分布式系统一致性的特点:
- 由于存在数据同步的过程,写操作的响应会有一定的延迟。
- 为了保证数据一致性会对资源暂时锁定,待数据同步完成释放锁定资源。
- 如果请求数据同步失败的结点则会返回错误信息,一定不会返回旧数据。
2.2 A 可用性
可用性是指任何客户端的请求都能得到响应数据,不会出现响应错误。
在上图读写分离的环境中,即时数据还没有同步过来,从数据库也要返回要查询的数据,哪怕是旧数据,如果连旧数据也没有则可以按照约定返回一个默认信息,但不能返回错误或响应超时。
2.3 P 分区容忍性
通常分布式系统的各各结点部署在不同的子网,这就是网络分区,不可避免的会出现由于网络问题而导致结点之间 通信失败,系统需要保证此时仍可对外提供服务,这叫分区容忍性。分区容忍性是分布式系统具备的基本能力,必须要实现。
在分布式环境下,为了保证分区容忍性,数据库会采用主从、集群、异地容灾等方式。
在上图读写分离的环境中,实现分区容忍性,需要保证主从同步失败时,不影响读写操作。其一个结点挂掉不影响另一个结点对外提供服务。
需要从以下几点进行实现:
- 尽量使用异步取代同步操作,例如使用异步方式将数据从主数据库同步到从数据
- 添加从数据库结点,其中一个从结点挂掉其它从节点提供服务。
2.4 组合方式
在所有分布式事务场景中不会同时具备CAP三个特性,因为在具备了P的前提下C和A是不能共存的。
分布式系统,肯定是需要满足分区容忍性,如果再满足一致性,对数据同步进行加锁,这样就没办法保证可用性了,因为可用性时,数据不一致,也需要查询到结果,A C始终是存在冲突的。
2.4.1 CA
放弃分区容忍性,即不进行分区,不考虑由于网络不通或结点挂掉的问题,则可以实现一致性和可用性。那么系统 将不是一个标准的分布式系统,我们最常用的关系型数据就满足了CA。
既然是单体,那么也就不存在分布式事务的概念了。。。。
2.4.2 AP
放弃一致性,追求分区容忍性和可用性。这是很多分布式系统设计时的选择。
AP 模式实现很简单,只需要保证集群环境下,数据同步正常即可,数据虽然可能更新后马上看不到最新的结果,但是最终的结果还是正确的,即保证最终一致性。
2.4.3 CP
放弃可用性,追求一致性和分区容错性。
也就是在分布式环境下,必须保证每次结果查询到的数据都是最新的,但是可能某个时段去查询,会显示数据不可用,即保证强一致性。
2.5 总结
一个分布式系统最多只能同时满足 一致性(Consistency)、可用性(Availability)和分区容忍性(Partition tolerance)这三项中的两项。可以作 为我们进行架构设计、技术选型的考量标准。
对于多数大型互联网应用的场景,结点众多、部署分散,而且现在的集群规模越来越大,所以节点故障、网络故障是常态,而且要保证服务可用性达到N个9(99.99…%),并要达到良好的响应性能来提高用户体验,因此一般都会做出如下选择:保证P和A,舍弃C强一致,保证最终一致性。
3 BASE理论
3.1 强一致性和最终一致性
CAP理论告诉我们一个分布式系统最多只能同时满足一致性(Consistency)、可用性(Availability)和分区容忍 性(Partition tolerance)这三项中的两项,其中AP在实际应用中较多,AP即舍弃一致性,保证可用性和分区容忍 性。
但是在实际生产中很多场景都要实现一致性,比如之前图片中主数据库向从数据库同步数据,即使不要一致性,但是最终也要将数据同步成功来保证数据一致,这种一致性和CAP中的一致性不同,CAP中的一致性要求在任何时间查询每个结点数据都必须一致,它强调的是强一致性,但是最终一致性是允许可以在一段时间内每个结 点的数据不一致,但是经过一段时间每个结点的数据必须一致,它强调的是最终数据的一致性。
3.2 Base理论
BASE是 Basically Available(基本可用)、Soft state(软状态)和 Eventually consistent (最终一致性)三个词语的缩写。
BASE理论是对CAP中AP的一个扩展,通过牺牲强一致性来获得可用性,当出现故障允许部分不可用但要保证 核心功能可用,允许数据在一段时间内是不一致的,但最终达到一致状态。满足BASE理论的事务,我们称之为“柔 性事务”。
3.2.1 基本可用
分布式系统在出现故障时,允许损失部分可用功能,保证核心功能可用。如电商网站交易付款出现问题了,商品依然可以正常浏览。
3.2.2 软状态
由于不要求强一致性,所以BASE允许系统中存在中间状态(也叫软状态),这个状态不影响系统可用性,如订单的"支付中"、“数据同步中”等状态,待数据最终一致后状态改为“成功”状态。
3.2.3 最终一致
最终一致是指经过一段时间后,所有节点数据都将会达到一致。如订单的"支付中"状态,最终会变 为“支付成功”或者"支付失败",使订单状态与实际交易结果达成一致,但需要一定时间的延迟、等待。
相关文章:

Seata入门系列【19】分布式事务之CAP、BASE理论
1 CAP理论 CAP是以下三个词语的缩写: Consistency:一致性Availability:可用性Partition tolerance:分区容忍性 CAP理论的基础概念就是在分布式系统中,无法同时满足以上三点。 下面我们以一个简单的分布式系统&…...

界面控件DevExpress WPF Gauge组件 - 轻松实现个性化商业仪表盘
DevExpress WPF Gauge(仪表)控件包含了多种圆形仪表类型、水平和垂直线性仪表、分段和矩阵数字仪表以及状态指示器,同时还具有最终用户交互性的集成支持。 P.S:DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至…...

算法题:870. 优势洗牌
该算法是临时想出来的,Java代码的实现在时间上不占优,之后有时间要优化一下,目前就是给大家提供一下思路。 解题思路:田忌赛马的思想 贪心法。 Step1. 对两个数组进行排序。 Step2. 同时遍历排序后的nums2和nums1,将…...

[架构之路-252/创业之路-83]:目标系统 - 纵向分层 - 企业信息化的呈现形态:常见企业信息化软件系统 - 企业应用信息系统集成
目录 第一章 什么是企业应用信息系统集成What 1.1 简介 1.2 架构 二、为什么需要企业应用信息系统集成Why 三、如何实现企业应用信息系统集成 3.1 步骤 3.2 企业应用集成的层次 3.3 业务流程重组 第一章 什么是企业应用信息系统集成What 1.1 简介 企业应用信息系统集…...

MFC发送http https以及json解析
域名解析成IP char szWeb[128] "www.baidu.com";struct hostent *pHost NULL;pHost gethostbyname(szWeb);//完成主机名到域名的解析char *IP inet_ntoa(*((struct in_addr *)pHost->h_addr));CString ipStr IP;请求三部曲: 1、CInternetSession…...
UE5加载websocket模块为空
今天测试UE 发现工程启动不了,后来看到原来是websocket模块无法加载。 解决的它的方法很简单,这种问题一般会出现在源码版本的引擎或者是停电了,导致UElaunch版本损坏,解决方法是来到源码版本的引擎 这个目录下: D:\…...

学习 Python 数据可视化,如何快速入门?
Python 是一种非常流行的编程语言,具有简单易学、高效、丰富的库和工具等特点。其中,数据可视化是 Python 的一个重要应用领域,可以帮助人们更好地理解和分析数据。本文将介绍如何快速入门 Python 数据可视化,以及常用的可视化工具…...

XUbuntu22.04之simplenote支持的Markdown语法总结(一百九十一)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

JAVA深化篇_26——Apache commons-io工具包的使用
Apache commons-io工具包的使用 Apache基金会介绍 Apache软件基金会(也就是Apache Software Foundation,简称为ASF),是专门为支持开源软件项目而办的一个非盈利性组织。在它所支持的Apache项目与子项目中,所发行的软…...

centos 7 kafka2.6单机安装及动态认证SASL SCRAM配置
目录 1.kfaka安装篇 1.1 安装jdk 1.2安装kafka 2.安全篇 2.1 kafka安全涉及3部份: 2.2 Kafka权限控制认证方式 2.3 SASL/SCRAM-SHA-256 配置实例 2.3.1 创建用户 2.3.2 创建 JAAS 文件及配置 3.测试 3.1 创建测试用户 3.2 配置JAAS 文件 3.2.1 生产者配…...
TrafficWatch 数据包嗅探器工具
TrafficWatch 是一种数据包嗅探器工具,允许您监视和分析 PCAP 文件中的网络流量。它提供了对各种网络协议的深入了解,并可以帮助进行网络故障排除、安全分析等。 针对 ARP、ICMP、TCP、UDP、DNS、DHCP、HTTP、SNMP、LLMNR 和 NetBIOS 的特定于协议的数据…...
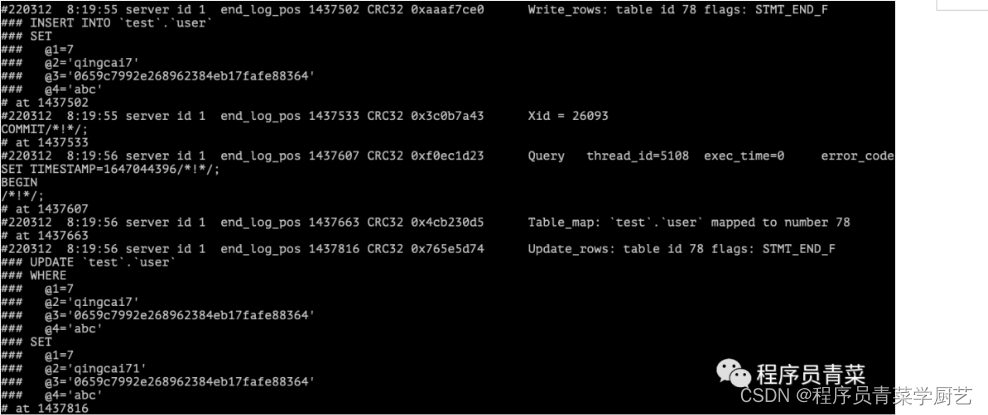
MySQL Binlog实战应用之一
一、前言 开发业务系统尤其是与财务相关的系统,需要记录每一笔变更操作的日志,这一般有两种实现方案。 1、代码中通过AOP实现,提供注解跟踪记录日志,这种方案能够比较清晰地以业务角度记录操作日志,但记录变更前的旧…...

【MySQL】MVCC机制(undo log,read view)
文章目录 前言一. 预备知识二. 模拟MVCC三. Read View四. RC与RR的本质区别结束语 前言 MVCC(多版本并发控制)是一种用来解决读-写冲突的无锁并发控制 MVCC为事务分配单向增长的事务ID,为每个修改保存一个版本,版本与事物ID相关联…...
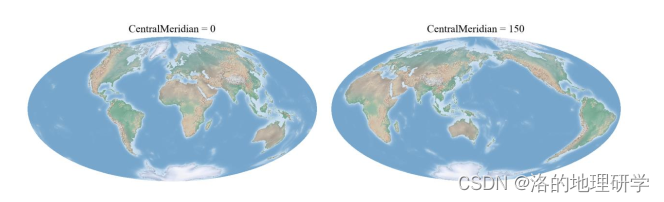
gma 2 教程(三)坐标参考系统:3.投影方法
安装 gma:pip install gma 地图投影是利用一定数学法则把地球表面的经、纬线转换到平面上的理论和方法。由于地球是一个赤道略宽两极略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变…...

蓝桥杯每日一题2023.11.2
题目描述 等差素数列 - 蓝桥云课 (lanqiao.cn) 题目分析 对于此题我们需要求出最小的公差并且长度为10, 1.确保序列开始为素数 2.确定枚举的个数 注意:序列中数只是d的变化,可以通过此计算将开始数字后9个数字都计算出来,d是…...

Leetcode67二进制求和
1104 代码: class Solution {public String addBinary(String a, String b) {StringBuffer ans new StringBuffer();int n Math.max(a.length(),b.length()),carry 0;for(int i0;i<n;i){carry i < a.length()?(a.charAt(a.length()-1-i)-0):0;carry i…...
线性代数 第五章 特征值与特征向量
一、特征值定义 二、特征值求法 定义法;;相似。 三、特征向量求法 定义法;基础解系法;;相似。 四、特征值性质 不同特征值的特征向量线性无关k重特征值至多有k个线性无关的特征向量 五、相似的定义 若ÿ…...
(python数据库))
Python嵌入式数据库 / 轻量级数据库 / 小型数据库介绍(SQLite、Pandas DataFrame、TinyDB)(python数据库)
文章目录 Python嵌入式数据库/轻量级数据库介绍什么是嵌入式数据库/轻量级数据库?SQLitePandasTinyDB总结 Python嵌入式数据库/轻量级数据库介绍 在构建应用程序时,数据存储是必不可少的一部分。传统的方式是使用如MySQL、PostgreSQL这样的重量级数据库…...

USB PD v1.0快速充电通信原理
1 原理 本篇文章讲的快速充电是指USB论坛所发布的USB Power Delivery快速充电规范(通过VBUS直流电平上耦合FSK信号来请求充电器调整输出电压和电流的过程),不同于本人发布的另一篇文章所讲的高通Quick Charger 2.0规范,因为高通QC…...
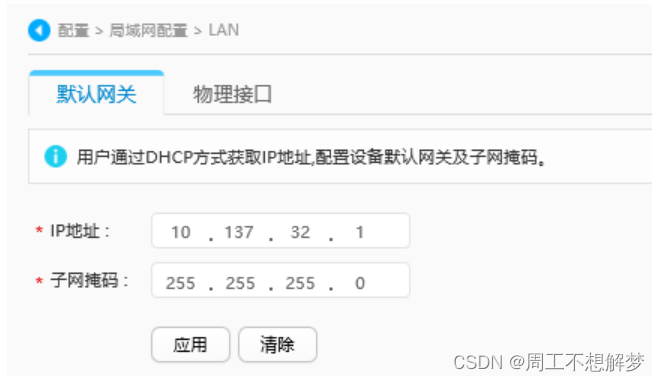
【华为】路由器以PPPoE拨号接入广域网
组网需求 用户希望以PPPoE拨号方式接入广域网,如图1所示,Router作为PPPoE客户端,得到PPPoE服务器的认证后获得IP地址,实现用户接入互联网的需求。内网网关地址(即VLANIF1接口的IP地址)为10.137.32.1/24。 …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

C#中用于控制自定义特性(Attribute)
我们来详细解释一下 [AttributeUsage(AttributeTargets.Class, AllowMultiple false, Inherited false)] 这个 C# 属性。 在 C# 中,Attribute(特性)是一种用于向程序元素(如类、方法、属性等)添加元数据的机制。Attr…...
