FRI及相关SNARKs的Fiat-Shamir安全
1. 引言
本文主要参考:
- Alexander R. Block 2023年论文 Fiat-Shamir Security of FRI and Related SNARKs
- Albert Garreta 2023年9月在ZK Summit 10上分享 ZK10: Fiat-Shamir security of FRI and related SNARKs - Albert Garreta (Nethermind)
评估参数用的Sagemath code见:
- https://github.com/alexander-r-block/FRI-Parameter-Testing-Sagemath
2. 何为FRI-based SNARK?
何为FRI-based SNARK?
非正式来说,其为遵循如下配方的SNARK:
- 1)PIOP:Polynomial Interactive Oracle proof。
- 2)FRI + Merkle trees:将PIOP用FRI和Merkle trees进行compile。
- 3)Fiat-Shamir transform
2.1 何为PIOP?
PIOP=Polynomial Interactive Oracle proof。
PIOP是一种交互协议,有Prover和Verifier两种角色,有problem statement x x x,和仅对Prover已知的witness w w w。Prover和Verifier以一定轮数相互交换消息。

PIOP的独特性在于:
- Prover发送的消息 m i ( X ) m_i(X) mi(X)为“low degree” polynomials。
- 在交互阶段结束时,Verifier会在random points来open这些 m i ( X ) m_i(X) mi(X)多项式,并基于这些openings是否满足某些代数关系,来决定是accept还是reject。
当在对PIOP做安全性分析时,一个关键假设是:
- 假设攻击者(恶意Prover)发送的所有maps都是多项式。【这实际是一个很强的假设,从而让PIOP安全性分析相对简单。】
这样,对PIOP的安全性分析,通常会归结为争论:
- 除非Verifier(非常不幸)恰巧发送了某特定low-degree polynomial的root,否则攻击者无法破坏该PIOP协议。
而根据Schwartz-Zippel lemma有:“degree d d d多项式具有 ≤ d \leq d ≤d个roots”。
因此,攻击者破解该PIOP协议的概率 ≤ d / 2 λ \leq d/2^{\lambda} ≤d/2λ。
PIOP是一种对ZKP进行分析的很好的抽象框架,但实际上,PIOP存在如下问题:
- 1)Verifier如何检查Prover发送的是low degree多项式?
- 方法之一是:Verifier检查这些多项式的所有evaluations,来确认其是否与某多项式一致,但这会让Verifier非常慢。
- 2)maps m i ( X ) m_i(X) mi(X)太大,难以发送。这会让proof size巨大,可能会与Prover直接发送witness size相当。
因此,针对以上PIOP问题的解决方案为:
- Polynomial Commitment Scheme(PCS)多项式承诺方案:即使用某多项式承诺方案对该PIOP进行编译。此时:
- PIOP中Prover发送的消息为 m i ( X ) m_i(X) mi(X)多项式的承诺值 C m ( m i ( X ) ) Cm(m_i(X)) Cm(mi(X)),而不再是 m i ( X ) m_i(X) mi(X)多项式本身。
- 在交互协议阶段结束时,为获得在随机点的openings m i ( a ) m_i(a) mi(a),由于此时Verifier只有 m i ( X ) m_i(X) mi(X)的承诺值,其无法自己open,因此Verifier会根据特定的PCS规则 与Prover交互,以获得openings m i ( a ) m_i(a) mi(a)。

目前的PCS多项式承诺方案有:
- KZG多项式承诺方案
- IPA-based多项式承诺方案
- (FRI + Merkle tree)-based多项式承诺方案:本文重点关注本方案。因很多从业人员常使用(FRI + Merkle tree)-based多项式承诺方案,但实际上其需要在非常严格地配置下,才能将FRI用作PCS多项式承诺方案。而这种严格配置,会让(FRI + Merkle tree)-based PCS很慢。
因此实际应用时,会将FRI配置为非PCS,后续将详谈这个关键点。
在Marlin和Dark等论文中,有如下定理:
- 若PIOP和PCS是安全的,则新协议是安全的。
2.2 Fiat-Shamir transform
Fiat-Shamir transformation可:
- 移除交互性
- 对public coin协议,所有Verifier消息都是随机的
- 简单思路为:将Verifier的challenges替换为hashes。
- 将哈希函数 模型化为 a Random Oracle。
借助Fiat-Shamir转换为非交互式协议之后:
- Verifier会基于 ( x , m 1 , c 1 , ⋯ , m μ ) (x,m_1,c_1,\cdots,m_{\mu}) (x,m1,c1,⋯,mμ)的有效性来决定是accept还是reject。
- Verifier会检查 c i c_i ci是否“well hashed”。
当前FRI-based SNARKs有:
- STARK
- Plonky2
- RISC Zero
- Boojum

3. Fiat-Shamir issues
3.1 Fiat-Shamir转换的安全性
令:
- Π \Pi Π为某交互式协议
- F S ( Π ) FS(\Pi) FS(Π)为其Fiat-Shamir转换
则,有可能 Π \Pi Π是安全的,但 F S ( Π ) FS(\Pi) FS(Π)是不安全的。
如:
- 示例一: Π \Pi Π为sequential repetition of a “small” protocol。如某small protocol的sound error为 1 / 2 1/2 1/2,交互式重复该协议2次,则sound error变为 ( 1 / 2 ) 2 = 1 / 4 (1/2)^2=1/4 (1/2)2=1/4。
当但对该small协议做FS转换获得新协议时,则可能是灾难——其security仍为 1 / 2 1/2 1/2。 - 示例二: Π \Pi Π为parallel repetition of a “smaller” protocol Π 0 \Pi_0 Π0(Attema, Fehr, Kloss, 2022)。【本文重点关注这种并行重复执行协议示例】
假设 Π 0 \Pi_0 Π0 small协议的安全性为 ϵ \epsilon ϵ,为增加其安全性,并行对其进行重复执行——以2倍并行为例,Prover在每轮会发送2个消息,Verifier在每轮会应答2个challenges。这就相当于以2个线程来并行运行 Π 0 \Pi_0 Π0。 Π \Pi Π的Verifier会accept,当且仅当, Π 0 \Pi_0 Π0的Verifier会同时accept ( x , m 1 , c 1 , m 2 , c 2 , m 3 ) (x,m_1,c_1,m_2,c_2,m_3) (x,m1,c1,m2,c2,m3)和 ( x , m 1 ′ , c 1 ′ , m 2 ′ , c 2 ′ , m 3 ′ ) (x,m_1',c_1',m_2',c_2',m_3') (x,m1′,c1′,m2′,c2′,m3′)。这样 Π \Pi Π的安全性将是 Π 0 \Pi_0 Π0的二次方,即 ϵ 2 \epsilon^2 ϵ2。

parallel repetition场景下的FS攻击,攻击者攻击流程为:
- 1)Prover选择 ( m 1 , m 1 ′ ) (m_1,m_1') (m1,m1′)
- 2)计算 ( c 1 , c 1 ′ ) = H a s h ( x , m 1 , m 1 ′ ) (c_1,c_1')=Hash(x,m_1,m_1') (c1,c1′)=Hash(x,m1,m1′)
- 3)检查 c 1 c_1 c1是否为某“special” challenge,其使得 Π 0 \Pi_0 Π0的第一个proof ( x , m 1 , c 1 , m 2 , c 2 , m 3 ) (x,m_1,c_1,m_2,c_2,m_3) (x,m1,c1,m2,c2,m3)是有效的。如, c 1 c_1 c1可为特定多项式的root。【因此,实际需确保Verifier发送的challenge不是多项式的root,否则将破坏协议。】
- 4)若 c 1 c_1 c1不是特殊的challenge,则Prover rewinds,然后重复执行上面的步骤1)。
【原则上,Prover需要 ≈ 1 / ϵ = 2 λ \approx1/\epsilon=2^{\lambda} ≈1/ϵ=2λ次迭代即可成功。其中 λ \lambda λ为交互式协议的安全参数。】

然后,假设Prover最终找到了该特殊的challenge c 1 c_1 c1,并继续如下流程: - 1)令 m 2 m_2 m2为某消息,使得Prover可获得第一个有效proof ( x , m 1 , c 1 , m 2 , c 2 , m 3 ) (x,m_1,c_1,m_2,c_2,m_3) (x,m1,c1,m2,c2,m3)。
- 2)然后在另一线程中,重复之前的流程:
- 2.1)选择任意 m 2 ′ m_2' m2′
- 2.2)计算 ( c 2 , c 2 ′ ) = H a s h ( x , m 1 , m 1 ′ , c 1 , c 1 ′ , m 2 , m 2 ′ ) (c_2,c_2')=Hash(x,m_1,m_1',c_1,c_1',m_2,m_2') (c2,c2′)=Hash(x,m1,m1′,c1,c1′,m2,m2′)。
- 2.3)检查 c 2 ′ c_2' c2′是否为某“special” challenge,其使得 Π 0 \Pi_0 Π0的第二个proof ( x , m 1 ′ , c 1 ′ , m 2 ′ , c 2 ′ , m 3 ′ ) (x,m_1',c_1',m_2',c_2',m_3') (x,m1′,c1′,m2′,c2′,m3′)是有效的。如, c 2 ′ c_2' c2′可为特定多项式的root。【因此,实际需确保Verifier发送的challenge不是多项式的root,否则将破坏协议。】
- 2.4)若 c 2 ′ c_2' c2′不是特殊的challenge,则Prover rewinds,然后重复执行上面的步骤2.1)。
【原则上,Prover需要 ≈ 1 / ϵ = 2 λ \approx1/\epsilon=2^{\lambda} ≈1/ϵ=2λ次迭代即可成功。其中 λ \lambda λ为交互式协议的安全参数。】

结论为:
- 假设Prover为Round 1找到了特殊的 c 1 c_1 c1,为Round 2找到了特殊的 c 2 c_2 c2。
- 则 ( x , m 1 , c 1 , m 2 , c 2 , m 3 ) (x,m_1,c_1,m_2,c_2,m_3) (x,m1,c1,m2,c2,m3)和 ( x , m 1 ′ , c 1 ′ , m 2 ′ , c 2 ′ , m 3 ′ ) (x,m_1',c_1',m_2',c_2',m_3') (x,m1′,c1′,m2′,c2′,m3′)均为有效proofs。
- 找到该特殊 c i c_i ci需要约 ≈ 1 / ϵ = 2 λ \approx 1/\epsilon=2^{\lambda} ≈1/ϵ=2λ次迭代尝试。
- 总共,Prover需要 1 / ϵ + 1 / ϵ = 2 / ϵ 1/\epsilon +1/\epsilon=2/\epsilon 1/ϵ+1/ϵ=2/ϵ次迭代尝试。
- 这样,安全性仅增加了1个bit,尽管期待的是增加2倍,原因在于parallel repetition的交互版本具有的soundness为 1 / ϵ 2 1/\epsilon^2 1/ϵ2。
- 总的来说,第2个parallel repetition对soundness没有任何贡献。

相关经验法则为: - 令 Π 0 \Pi_0 Π0为 soundness error为 ϵ \epsilon ϵ的 μ \mu μ-round协议
- Π 0 ′ \Pi_0' Π0′为并行重复 Π 0 \Pi_0 Π0 t t t 次。
- 则 F S ( Π 0 ′ ) FS(\Pi_0') FS(Π0′)具有的soundness error 为 ≈ ϵ ⌈ t / μ ⌉ \approx \epsilon ^{\left \lceil t/\mu \right \rceil} ≈ϵ⌈t/μ⌉。
- 因此,所添加的 Π 0 \Pi_0 Π0并行实例个数,应为 μ \mu μ的倍数,才能实现在FS转换前类似的soundness。

3.2 何时FS转换是安全的?
以上面的结论和经验法则可知,存在如下情况:
- Π 0 ′ \Pi_0' Π0′具有soundness ϵ ′ \epsilon' ϵ′,但 F S ( Π 0 ′ ) FS(\Pi_0') FS(Π0′)具有低得多的soundness。
那么,问题来了,何时FS转换能保持相同量级的soundness?即何时FS转换后的协议与初始的交互协议具有相同的安全级别?
有2种概念:
- 1)Special soundness(Atttema, Fehr, Kloss, 2022):即证明初始交互协议满足某种特殊的soundness强概念。若初始交互协议是special sound的,则FS转换后的协议与该初始协议一样安全。
- 2)Round-by-Round (RBR) knowledge soundness(Chiesa, Manohar, Spooner, 2020):即若证明初始交互协议具有Round-by-Round (RBR) knowledge soundness,则FS转换后的协议与该初始协议一样安全。
所谓Round-by-Round (RBR) knowledge soundness:
- 在之前的2个例子(Sequential repetition和Parallel repetition)中,可称其为 “the overall soundness ϵ \epsilon ϵ of Π \Pi Π is the accumulation of smaller soundness errors throughout Π \Pi Π’s rounds”。
- 但这正是之前FS攻击所利用之处:攻击者其可rewind proofs,并试图破坏该small soundness checks,这些checks具有small soundness,然后Fiat-Shamir transform将不再按预期工作。
- 当满足如下情况时,则称该协议是RBR (knowledge) sound的:【协议的安全性,不是多个不太安全checks的累加】
- 即,当“each round of Π \Pi Π has soundness error ≈ \approx ≈ the overall error ϵ \epsilon ϵ of Π \Pi Π”时。
在Theorem (Block, G., Tiwari, Zajac) 中指出:
- RBR knowledge soundness => special soundness => RBR soundness。
4. FRI及其FS安全性
FRI协议:
- FRI是a IOP。
- FRI Prover具有某函数 f : F → F f:\mathbb{F}\rightarrow \mathbb{F} f:F→F。
- FRI Verifier可访问所有的 f ( v ) f(v) f(v),其中 v ∈ D v\in D v∈D, D ⊆ F D\subseteq \mathbb{F} D⊆F。
- 理想情况下,FRI协议的目的是:让Verifier信服 f ( X ) f(X) f(X)为某degree ≤ d \leq d ≤d的多项式。
- 实际情况下,FRI协议的目的是:让Verifier信服 f ( X ) f(X) f(X) 为 δ \delta δ-close 某degree ≤ d \leq d ≤d的多项式。
- 所谓 δ \delta δ-close,是指:在 D D D的相对大的子集 D 0 D_0 D0内, f ( X ) f(X) f(X)与某low degree多项式 agree,即 ∣ D 0 ∣ ≥ ( 1 − δ ) ∣ D ∣ |D_0|\geq (1-\delta)|D| ∣D0∣≥(1−δ)∣D∣,且 0 < δ < 1 0<\delta <1 0<δ<1。
Theorem (Block, G., Katz, Thaler, Tiwari, Zajac; StarkWare) 中指出:
- FRI协议是RBR (knowledge) sound的。【根据之前的RBR knowledge soundness => special soundness => RBR soundness,可知FRI协议也是special sound的。】
因此,FRI协议FS转换之后,其soundness ≈ Q ε F R I + Q 2 2 \approx \mathcal{Q}_{\varepsilon_{FRI}}+\frac{\mathcal{Q}^2}{2} ≈QεFRI+2Q2。即,可安全的对FRI进行Fiat-Shamir转换。
5. 使用FRI来编译PIOPs
5.1 FRI-based PCS in practice
当 “ δ \delta δ-close” 是 “very close”时,FRI可用于构建多项式承诺:
- 为验证 f ( z ) = y f(z)=y f(z)=y,需使用FRI来检查:“ q ( X ) : = f ( X ) − y X − z q(X):=\frac{f(X)-y}{X-z} q(X):=X−zf(X)−y” 为 “ δ \delta δ-close” to 某degree ≤ d − 1 \leq d-1 ≤d−1 多项式。
- 此处“very close”,是指:在 某unique decoding radius δ ≤ ( 1 − ( d + 1 ) / ∣ D ∣ ) / 2 \delta\leq (1-(d+1)/|D|)/2 δ≤(1−(d+1)/∣D∣)/2范围内。
- 但是,取如此小的 δ \delta δ值,在效率上是有开销的。会导致不具备实用性的不高效的FRI协议。也就是说,实际应用时,并不会取如此低的proximity参数。
- 实际上,当前所有的协议(如STARK、Plonky2、RISC Zero等),会取更大的proximity参数 δ \delta δ值,其最大为Johnson bound: 1 − ( d + 1 ) / ∣ D ∣ 1-\sqrt{(d+1)/|D|} 1−(d+1)/∣D∣。
- 这样的实际取值,导致以上"PCS"将不再是一个多项式承诺方案。原因在于:
- 可能有多个多项式,其均满足 δ \delta δ-close to the map q ( X ) q(X) q(X)。
- Prover可open这多个close多项式中的任意一个。【此时,Prover不再是对某多项式进行commit,而是对一组多项式进行commit。这是个问题。】
- 将FRI用作PCS beyond unique decoding radius的相关项目有:
- RedShift:Plonk + FRI —— 其soundness error随execution trace width指数级扩大。
- STARK-type协议:DEEP-FRI、ethSTARK等 + Hab¨ock。【其使用FRI来编译PIOPs,当不将FRI看成是多项式承诺方案。】【Polygon Labs Ulrich Hab¨ock 2022年论文《A summary on the FRI low degree test》中,对所评估的soundness进行了一点改进。】
为此,主要结论为:
- Theorem (Block, G., Katz, Thaler, Tiwari, Zajac) 中指出:有某large class C \mathscr{C} C of PIOPs,使得:
- 假设该初始PIOP是RBR (knowledge) sound的。
- 则所生成的FRI-based SNARG是knowledge sound的,即为a SNARK。
因此,关键点在于:
- 以上Theorem支持,仅通过看该PIOP,来证明该SNARK的安全性。这样通常相对更易于分析。
Alexander R. Block 2023年论文 Fiat-Shamir Security of FRI and Related SNARKs 中:
- 展示了ethSTARK和Plonky2作为PIOPs是RBR knowledge sound的,且在class C \mathscr{C} C中。
- 从而可推断出:ethSTARK和Plonky2作为SNARGs是knowledge sound的。
- 与此同时,StarkWare也展示了ethSTARK的相同结论。
- 称PIOPs in C \mathscr{C} C 0 0 0-correlated。

参考资料
[1] Alexander R. Block 2023年论文 Fiat-Shamir Security of FRI and Related SNARKs
[2] Albert Garreta 2023年9月在ZK Summit 10上分享 ZK10: Fiat-Shamir security of FRI and related SNARKs - Albert Garreta (Nethermind)
相关文章:

FRI及相关SNARKs的Fiat-Shamir安全
1. 引言 本文主要参考: Alexander R. Block 2023年论文 Fiat-Shamir Security of FRI and Related SNARKsAlbert Garreta 2023年9月在ZK Summit 10上分享 ZK10: Fiat-Shamir security of FRI and related SNARKs - Albert Garreta (Nethermind) 评估参数用的Sage…...
TensorFlow案例学习:使用 YAMNet 进行迁移学习,对音频进行识别
前言 上一篇文章 TensorFlow案例学习:简单的音频识别 我们简单学习了音频识别。这次我们继续学习如何使用成熟的语音分类模型来进行迁移学习 官方教程: 使用 YAMNet 进行迁移学习,用于环境声音分类 模型下载地址(需要科学上网&…...

MySQL CHAR 和 VARCHAR 的区别
文章目录 1.区别1.1 存储方式不同1.2 最大长度不同1.3 尾随空格处理方式不同1.4 读写效率不同 2.小结参考文献 在 MySQL 中,CHAR 和 VARCHAR 是两种不同的文本数据类型,CHAR 和 VARCHAR 类型声明时需要指定一个长度,该长度指示您希望存储的最…...

虚拟机 ping: www.baidu.com:未知的名称或服务
1、打开ifcfg-ens33文件 vi /etc/sysconfig/network-scripts/ifcfg-ens332、如下,加上网关和dns就行了,紫色部分,也就是DNS1“114.114.114.114” TYPE"Ethernet" PROXY_METHOD"none" BROWSER_ONLY"no" BOOTP…...
第二章 Python字符串处理
系列文章目录 第一章 Python 基础知识 第二章 python 字符串处理 第三章 python 数据类型 第四章 python 运算符与流程控制 第五章 python 文件操作 第六章 python 函数 第七章 python 常用内建函数 第八章 python 类(面向对象编程) 第九章 python 异常处理 第十章 python 自定…...

混合编程 ATPCS规范及案例(汇编调用C、C调用汇编、内联汇编)
1.混合编程的规范 2.汇编调用C 2.C调用汇编 3.内联汇编 例子:...

使用Gorm进行CRUD操作指南
使用GORM在Go中创建、读取、更新和删除记录的逐步教程 在数据库管理中,CRUD操作是应用程序的支柱,它们使数据的创建、检索、更新和删除成为可能。强大的Go对象关系映射库GORM通过抽象SQL语句的复杂性,使这些操作变得轻松。本文将作为您全面指…...
Linux0.11内核源码解析-exec.c
主要实现对二进制可执行文件和shell文件的加载和执行,其中主要的函数是do_execve(),它是系统中断调用int 0x80的功能号__NR_execve()调用,是exec()函数的主要实现以下几点功能: 1.执行对参数和环境参数空间页面的初始化操作,初始…...

百度竞价排名推广对比自然排名哪一个更具优势-华媒舍
在搜索引擎结论网页页面(SERP)中,我们经常会看到一些网站链接及其广告栏。这种连接一般分为两种类型:百度竞价推广排名推广与自然排名。究竟哪个更有优势?本文将对这几种排名形式进行科谱详细介绍。 什么叫百度竞价推广…...
python第一课 变量
1.离线的情况下首选txt文档 2.有道云笔记 3.思维导图 xmind mindmaster 4.博客 5.wps流程图 # 变量的命名规则 1.变量名只能由数字字母下划线组成 2.变量名不能以数字开头 3.变量名不能与关键字重名 快捷键 撤销:Ctrl/Command Z 新建:Ctrl/Com…...

shell之netstat的用法
shell之netstat的用法 所有参数应用举例 所有参数 1)-A<网络类型>或–<网络类型> 列出该网络类型连线中的相关地址。 2)-i 显示所有网络接口的信息。 3)-r 显示路由表的信息。 4)-s 显示按各个协议的统计信息。 5&am…...
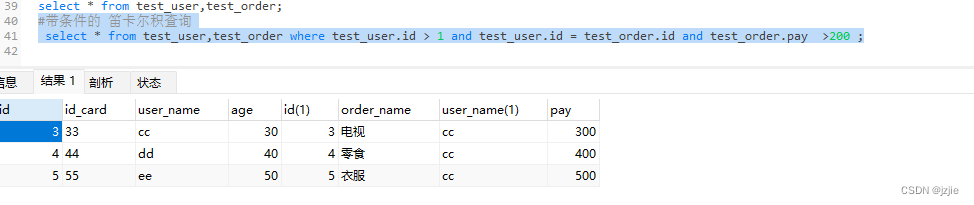
MSQL系列(十二) Mysql实战-为什么索引要建立在被驱动表上
Mysql实战-为什么索引要建立在被驱动表上 前面我们讲解了BTree的索引结构,也详细讲解下 left Join的底层驱动表 选择原理,那么今天我们来看看到底如何用以及如何建立索引和索引优化 开始之前我们先提一个问题, 为什么索引要建立在被驱动表上…...

C语言,数据结构指针,结构构体操作符 •,->,*的区别,看这篇就够了
在朋友们学习指针和数据结构这一章的时候,对各种操作符云里雾里。当你看到这么文章之后你就会明白了。 一 • 和 ->运算符 • 运算符:是结构变量访问结构体成员时用的操作符 -> 运算符:这是结构体指针访问结构体成员时调用的运算符。 …...

axios 多个baseURL配置、实现不同前缀代理到不同的服务器的几种方式
前言: 在开发中,有可能遇到每部分的功能的需要调用另一台服务器的地址。这个时候就需要设置不同的请求前缀首先代理到不同的服务器地址。 一、axios封装实例以及代理:(不是完整的封装实例,重点在于baseURL的区别) 文件路径&…...
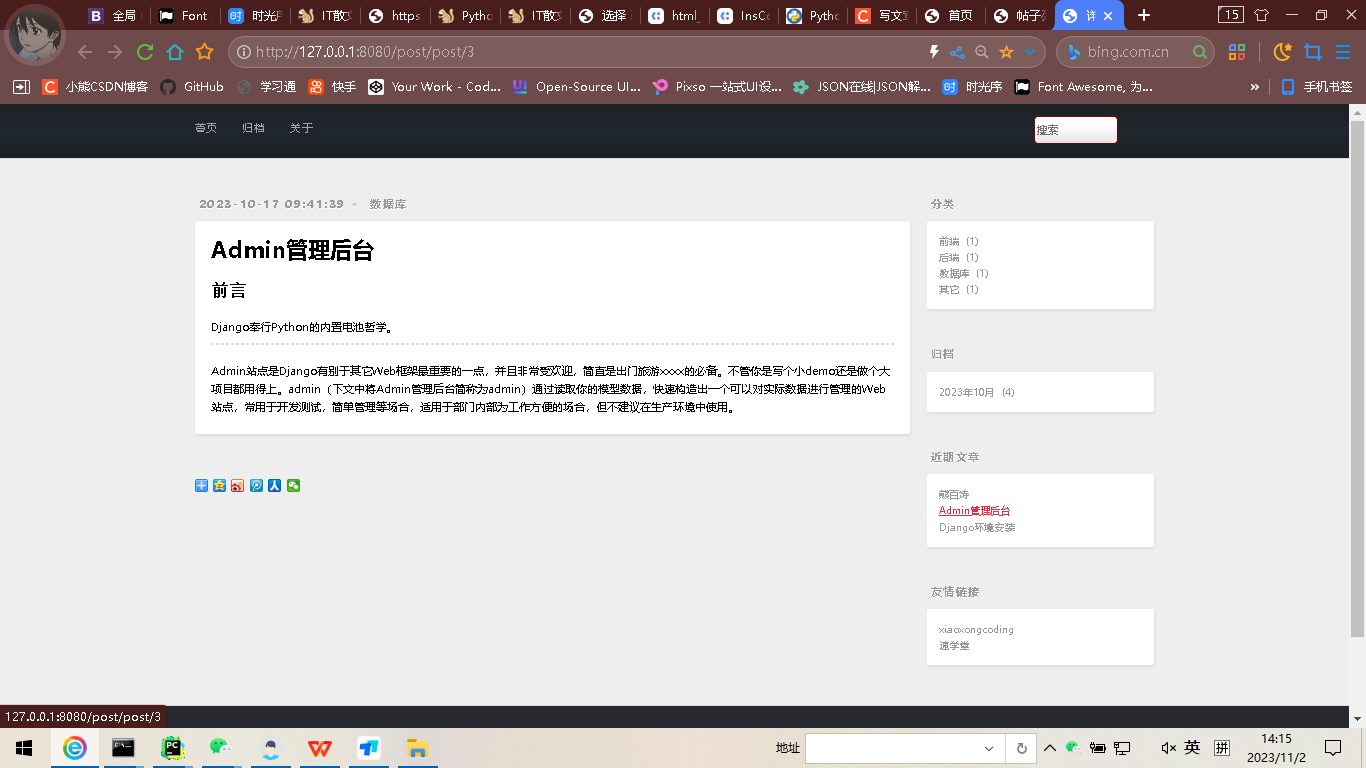
Diango项目-简易个人博客项目
项目实现功能 在admin后台自定义添加上传文档。对展示在首页的文章分页显示。在首页点击文章的阅读全文按钮可进入该文章全文详情页进行浏览。对文章实现了内容分类何以发布时间进行归档分类。使用django的whoose搜索引擎对全文实现内容的搜索。 项目涉及技术 Mysql Djan…...

思维训练3
题目描述1 Problem - A - Codeforces 题目分析 样例1解释: 对于此题,我们采用贪心的想法,从1到n块数越少越好,故刚好符合最少的块数即可,由于第1块与第n块是我们必须要走的路,所以我们可以根据这两块砖的…...

初识FFmpeg
前言 无意间见到群里的小伙伴展示视频工具。功能比较多,包括视频编码修改,画质处理,比例处理、名称提取,剪辑、标题拆解。因此开始了FFmpeg学习。以下摘自百度百科的解释。 FFmpeg是一套可以用来记录、转换数字音频、视频…...

分布式多主关系数据库的底线业务优势
当今的应用程序(包括企业应用程序)需要始终开启且始终可用,并且通常必须为全球用户提供服务,这些用户无论身在何处都希望获得几乎即时的响应时间。 应对这些挑战不仅仅意味着让用户更满意:每个能够解决低延迟和超高可…...
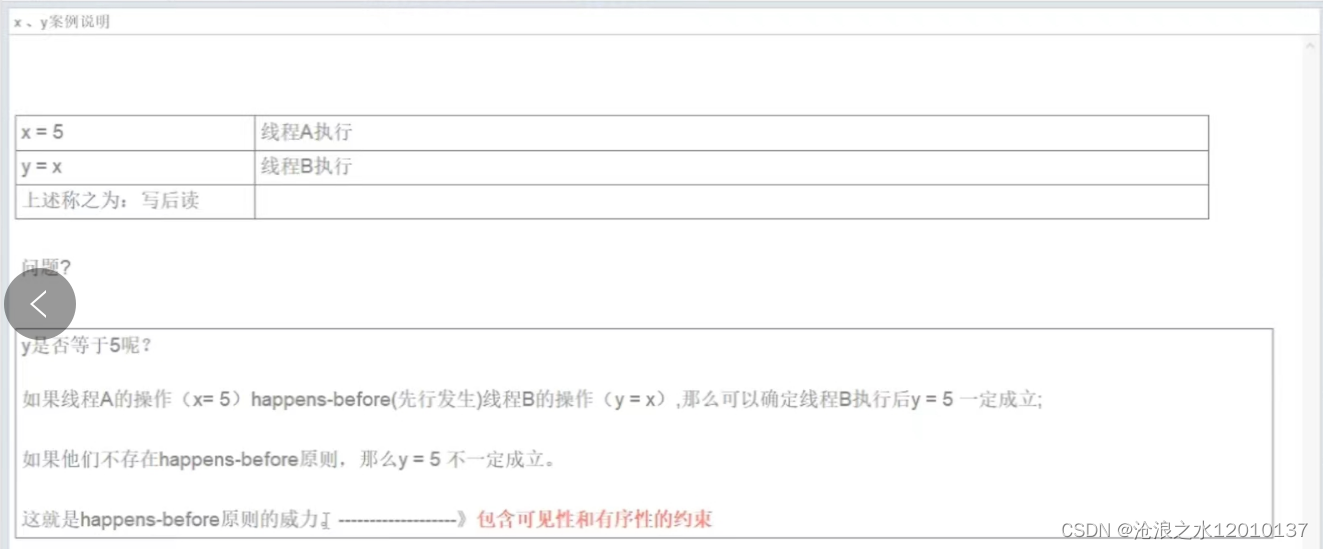
JMM讲解
一:为什么要有JMM,它为什么出现? CPU的运行并不是直接操作内存而是先把内存里面的数据读到缓存,而内存的读和写操作的时候会造成不一致的问题。JVM规范中试图定义一种Java内存模型来屏蔽掉各种硬件和操作系统的内存访问差异&…...
小程序获取头像和昵称的思路
小程序获取头像和昵称的基本方法是调用小程序自带的API wx.getUserProfile(),这也是小程序官方目前最推荐的做法。成功获取用户名头像之后,小程序允许保存调用的结果,以便下一次打开页面的时候自动显示头像和名字。保存用户名和头像并不是保存…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...
