NOIP2023模拟10联测31 迷路
题目大意
你在野外迷路了, 你手里只有一张你当前所在的区域的地图。地图将整个区域表示为 n × m n\times m n×m的网格,你就在其中的某一个格子里。每个格子里要么有树,要么就什么都没有。地图显示了每个格子中是有树还是空的。当然,地图只记载了这个区域的情况,你可以认为地图外的地方是一片无限延伸的空地(没有树)。你现在可以做的就是探索这个区域,以找到你的出发点(保证你的出发点一开始一定在地图内)。你会按照螺旋形的顺序探索这个区域: 先往下一格,然后往右一格,接着往上一格,接着往上一格,接着往左一格,接着往左一格,接着往下一格… …下面演示了这种顺序,数字代表你探索的顺序。在一个网格中,你能知道的唯一信息就是这里是否有一棵树。地图上的区域中有 k k k个格子是有树的。
20 19 18 17 16 21 6 5 4 15 22 7 0 3 14 23 8 1 2 13 24 9 10 11 12 20 \ 19 \ 18 \ 17 \ 16 \\ 21 \ \ 6 \ \ \ 5 \ \ \ 4 \ \ 15 \\ 22 \ \ 7 \ \ \ 0 \ \ \ 3 \ \ 14 \\ 23 \ \ 8 \ \ \ 1 \ \ \ 2 \ \ 13 \\ 24 \ \ 9 \ \ 10 \ 11 \ 12 20 19 18 17 1621 6 5 4 1522 7 0 3 1423 8 1 2 1324 9 10 11 12
现在你遇到了一个商人,他会告诉你地图上的 r r r个坐标,其中一个坐标就是你的起点。你想计算出如果你从所有 n × m n\times m n×m个格子中等概率地选择 r r r个格子,你为了区分起始点所需走的步数的期望值。
“你为了区分起始点所需走的步数”指的是,对于给定的 r r r个可能的起始点中的任意一个起点,你都要通过在这几步内得到的信息判断出你在这 r r r个点中应该是从这个点开始的,所需走的最少步数。步数是你探索的网格数(因此起始网格被视为一步)。
输入有四个数 n , m , k , r n,m,k,r n,m,k,r,然后有 k k k行,每行两个数 x , y x,y x,y,表示一个有树的格子的坐标。保证坐标两两不同。
输出期望值模 998244353 998244353 998244353后的值。
1 ≤ n , m ≤ 300 , 1 ≤ k , r ≤ min ( n × m , 300 ) 1\leq n,m\leq 300,1\leq k,r\leq \min(n\times m,300) 1≤n,m≤300,1≤k,r≤min(n×m,300)
题解
我们考虑对于每一步,维护每个起点收到的信息的等价类,那么我们能区分这 r r r个点当且仅当这 r r r个点所在不同的等价类互不相同,这个的概率可以用 D P DP DP算出。时间复杂度为 O ( n 2 m 2 r ) O(n^2m^2r) O(n2m2r)。
我们考虑维护等价类,一共有 n m nm nm步,维护每一步的时间复杂度为 O ( n m ) O(nm) O(nm),所以总时间复杂度是 O ( n 2 m 2 ) O(n^2m^2) O(n2m2)的。但是我们发现树的数量比较少,所以可以用每棵树来更新每个点。于是,对于每一步,将当前这一步有树的起点从其所在的等价类中单独剥离出来,这样总时间复杂度就变为 O ( n m k ) O(nmk) O(nmk)的了。
考虑朴素 D P DP DP:设 f i , j f_{i,j} fi,j表示在前 i i i个等价类中选择了 j j j个数,使得它们在不同等价类中的方案数。这样每次计算的时间复杂度为 O ( n m r ) O(nmr) O(nmr),总时间复杂度为 O ( n 2 m 2 r ) O(n^2m^2r) O(n2m2r)。考虑优化,设当前等价类的大小分别为 a 1 , a 2 , … , a p a_1,a_2,\dots,a_p a1,a2,…,ap,那么方案数为 [ x r ] ∏ i = 1 p ( 1 + a i x ) [x^r]\prod\limits_{i=1}^p(1+a_ix) [xr]i=1∏p(1+aix)。我们可以实时维护后面的多项式,因为等价类最多只会有 n m nm nm次分裂,每次将一个大小为 a a a的等价类分为 b b b和 c c c时,对这个多项式进行的操作就是除以 ( 1 + a x ) (1+ax) (1+ax)然后乘上 ( 1 + b x ) ( 1 + c x ) (1+bx)(1+cx) (1+bx)(1+cx),这些都可以在 O ( r ) O(r) O(r)的时间复杂度下完成,所以总时间复杂度为 O ( n m r ) O(nmr) O(nmr)。
总时间复杂度为 O ( n m k + n m r ) O(nmk+nmr) O(nmk+nmr)。
可以参考代码帮助理解。
code
#include<bits/stdc++.h>
using namespace std;
const int N=300;
const long long mod=998244353;
int n,m,k,R,mx=0,tot=1,x[N+5],y[N+5],z[2*N+5][2*N+5];
long long lst,ans,jc[N*N+5],ny[N*N+5],a[N*N+5];
vector<int>w[N*N+5],v[N*N+5];
set<int>s;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void init(){jc[0]=1;for(int i=1;i<=N*N;i++) jc[i]=jc[i-1]*i%mod;ny[N*N]=mi(jc[N*N],mod-2);for(int i=N*N-1;i>=0;i--) ny[i]=ny[i+1]*(i+1)%mod;
}
long long C(int x,int y){return jc[x]*ny[y]%mod*ny[x-y]%mod;
}
void del(int v){for(int i=1;i<=R;i++) a[i]=(a[i]-a[i-1]*v%mod+mod)%mod;
}
void add(int v){for(int i=R;i>=1;i--) a[i]=(a[i]+a[i-1]*v)%mod;
}
int main()
{
// freopen("lost.in","r",stdin);
// freopen("lost.out","w",stdout);init();scanf("%d%d%d%d",&n,&m,&k,&R);if(R==1){printf("0");return 0;}for(int i=1;i<=k;i++){scanf("%d%d",&x[i],&y[i]);}z[300][300]=1;for(int i=1;i<=300;i++){for(int j=-i+1;j<=i;j++) z[300+i][300+j]=++tot;for(int j=i-1;j>=-i;j--) z[300+j][300+i]=++tot;for(int j=i-1;j>=-i;j--) z[300-i][300+j]=++tot;for(int j=-i+1;j<=i;j++) z[300+j][300-i]=++tot;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){int id=(i-1)*m+j;for(int p=1;p<=k;p++){w[id].push_back(z[300+x[p]-i][300+y[p]-j]);}sort(w[id].begin(),w[id].end());}}sort(w+1,w+n*m+1);for(int i=2;i<=n*m;i++){int p;for(int j=0;j<k;j++){if(w[i-1][j]!=w[i][j]){p=w[i-1][j]-1;mx=max(mx,p);break;}}v[p].push_back(i);}a[0]=1;add(n*m);s.insert(1);s.insert(n*m+1);for(int i=0;i<=mx;i++){for(int j=0;j<v[i].size();j++){int p=v[i][j];set<int>::iterator it=s.upper_bound(p);int l=*(prev(it)),r=(*it);del(r-l);add(p-l);add(r-p);s.insert(p);}ans=(ans+(a[R]-lst+mod)%mod*(i+1)%mod)%mod;lst=a[R];}ans=ans*mi(C(n*m,R),mod-2)%mod;printf("%lld",ans);return 0;
}
相关文章:

NOIP2023模拟10联测31 迷路
题目大意 你在野外迷路了, 你手里只有一张你当前所在的区域的地图。地图将整个区域表示为 n m n\times m nm的网格,你就在其中的某一个格子里。每个格子里要么有树,要么就什么都没有。地图显示了每个格子中是有树还是空的。当然,地图只记载…...

React Query + Redux toolkit 封装异步请求
当你需要进行 Redux 和 React Query 的组合时,除了常规的 Redux 方法(例如手动派发 action 和更新 state),还可以使用 createSlice 和 React Query 进行组合,这可以让你更方便地封装异步请求和更容易地更新状态。 使用…...
CSS基础知识点速览
1 基础认识 1.1 css的介绍 CSS:层叠样式表(Cascading style sheets) CSS作用: 给页面中的html标签设置样式 css写在style标签里,style标签一般在head标签里,位于head标签下。 <style>p{color: red;background-color: green;font-size…...
Windows 时间服务配置和配置工具
文章目录 Windows 时间服务保留Portw32tm 命令配置 Windows 时间服务配置客户端使用两个时间服务器配置客户端自动从域源同步时间检查客户端时间配置使用本地组策略编辑器配置Windows 时间注册表参考推荐阅读 Windows 时间服务 (W32Time) 为 Active Directory 域服务 (AD DS) 管…...
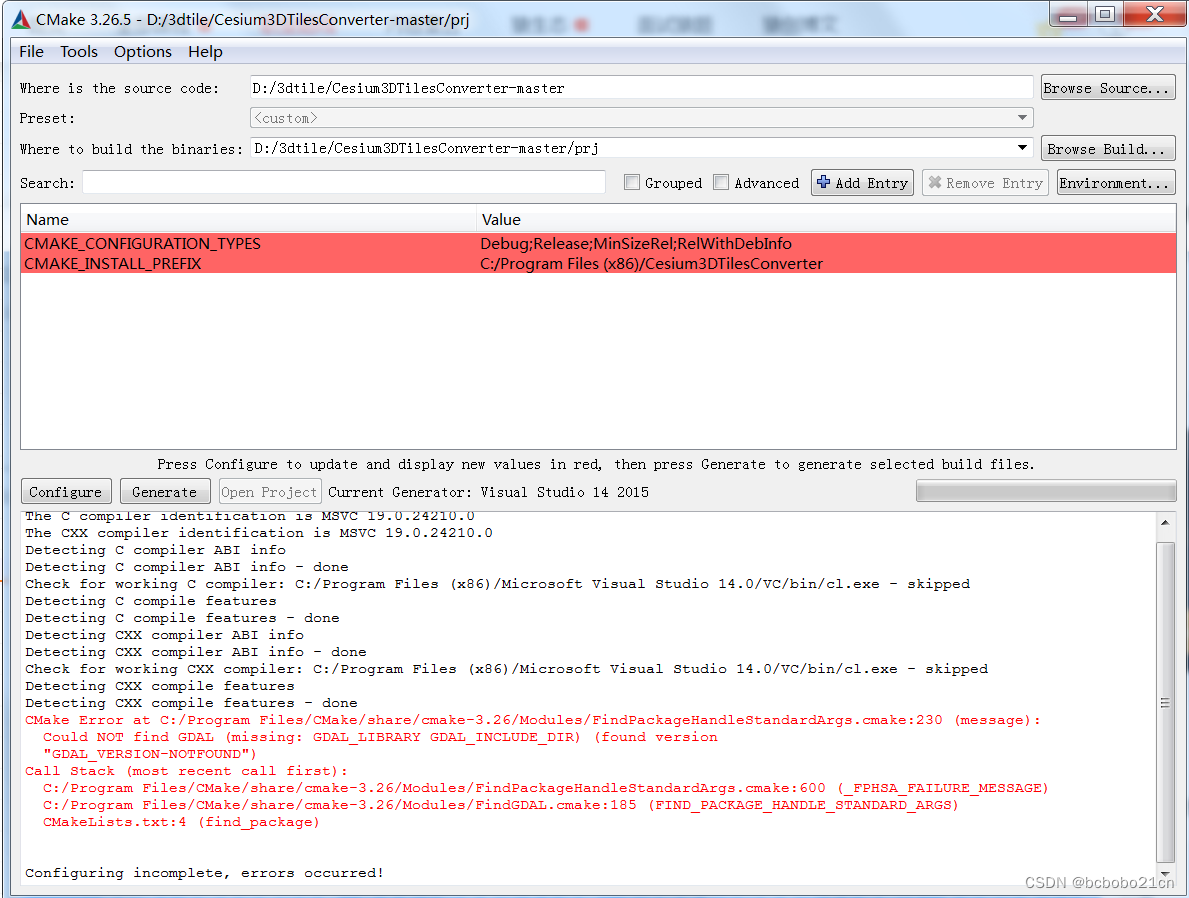
cmake find_package、引用GDAL 初步学习
上次的源码的CMakeLists.txt文件里有 find_package(GDAL REQUIRED) 这句; 从字面意思看此源码需要GDAL库; 查了一下,find_package 指令的基本功能是查找第三方库,并返回其细节; 我当前GDAL安装在D:\GDAL; 先把它的CMakeLists.txt重命名为别的,不使用; 新建一个C…...

紫光同创FPGA编写的8画面分割器演示
适用于板卡型号: 紫光同创PGL50H开发平台(盘古50K开发板) 图(1) 盘古50K开发板 TOP 层逻辑框 图(2) TOP层逻辑框 video_copy_ux 将输入的一路RGB888信号复制成8份,每份画面内容相同,各路颜色有些差异: 第…...
openLayers--绘制多边形、获取视图的中心点、获取当前地图等级、设置地图等级
openLayers绘制多边形、获取视图中心点 前言效果图1、导入LineString2、创建添加多边形3、定义多变形样式4、获取当前视图的中心点5、获取当前视图等级6、设置地图等级 前言 上一篇文章在vue项目中绘制了openlayers绘制了地图和标记点,本篇文章讲解openlayers绘制多…...

CSP-31补题日记--梯度求解
202309-3-梯度求解 题目链接 http://118.190.20.162/view.page?gpidT173 最近刚刚在上数据结构二叉树 跟这道题真的是强相关 然后在就是涉及到了数学求导 这基本上是我复学两个月做的最久的题了 感觉做完这道题对栈和二叉树理解比以前清晰了很多 不摆了 上代码 ** 题目思路&am…...

MySQL 8.0.32 union 语句中文查不到数据
关键字 MySQL union 语句,中文查不到数据 问题描述 MySQL 8.0.32 union 语句,中文查不到数据 解决问题思路 1、Create a table test with two fields, such as id and name mysql>create table test ( id int unsigned auto_increment key, name…...

FlinkCDC系列:通过skipped.operations参数选择性处理新增、更新、删除数据
在flinkCDC源数据配置,通过debezium.skipped.operations参数控制,配置需要过滤的 oplog 操作。操作包括 c 表示插入,u 表示更新,d 表示删除。默认情况下,不跳过任何操作,以逗号分隔。配置多个操作ÿ…...

高压检测设备
比如:高压数字表、高压差分探头、指针式高压表、电流探枪、高压探棒 这些设备都是用来测量高压的,有的测电压,有的测电流。 高压数字表: 单独使用,功能很简单,有2个正负极探爪,把2个探爪连接到…...

Vue3问题:如何实现组件拖拽实时预览功能?
前端功能问题系列文章,点击上方合集↑ 序言 大家好,我是大澈! 本文约3000字,整篇阅读大约需要5分钟。 本文主要内容分三部分,第一部分是需求分析,第二部分是实现步骤,第三部分是问题详解。 …...

基于jsp的采购管理系统的分析与实现
物资采购管理系统是针对内部而设计的,应用于的局域网,这样可以使得内部管理更有效的联系起来。企业采购管理系统是将IT技术用于企业采购信息的管理, 它能够收集与存储企业采购的档案信息,提供更新与检索企业采购信息档案的接口;提…...

react配置二级路由
1.在createBrowserRouter上添加basename属性,比如 const RouterRender createBrowserRouter([{path: /,element: <App><Login></Login></App>},...SystemRouter,...InventoryRouter,...FlowManageRouter,{path: "*",element: &…...
C++ 模板特化
非类型模板参数 定义:对于函数模板和类模板,模板参数并不局限于类型,普通值也可以作为模板参数 非类型模板参数定义的是常量 template<typename T, size_t N> class array; //T:类型模板参数 //N:非类型模板参…...

Spring-createBean部分源码
createBean源码: /*** Central method of this class: creates a bean instance,* populates the bean instance, applies post-processors, etc.* see #doCreateBean*/ Override protected Object createBean(String beanName, RootBeanDefinition mbd, Nullable …...

2015年亚太杯APMCM数学建模大赛C题识别网络中的错误连接求解全过程文档及程序
2015年亚太杯APMCM数学建模大赛 C题 识别网络中的错误连接 原题再现 网络是描述真实系统结构的强大工具——社交网络描述人与人之间的关系,万维网描述网页之间的超链接关系。随着现代技术的发展,我们积累了越来越多的网络数据,但这些数据部…...
和空值合并运算符(??))
js:可选链运算符(?.)和空值合并运算符(??)
文档: 可选链运算符(?.)https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Operators/Optional_chaining空值合并运算符(??)https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Referenc…...

【Java 进阶篇】Java ServletContext功能:获取文件服务器路径
Java ServletContext是Java EE中的一个核心接口,用于与Servlet容器进行通信,提供了许多有用的功能,包括获取文件服务器路径。在本文中,我们将详细介绍如何使用ServletContext来获取文件服务器路径,并提供示例代码以帮助…...

Android startActivity流程
1.常规调用 startActivity(new Intent(this,MainActivity.class)); 进入Activity的startActivity方法 /*** Same as {link #startActivity(Intent, Bundle)} with no options* specified.** param intent The intent to start.** throws android.content.ActivityNotFoundExc…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
