AC修炼计划(AtCoder Regular Contest 163)
传送门:AtCoder Regular Contest 163 - AtCoder
第一题我们只需要将字符串分成两段,如果存在前面一段比后面一段大就成立。
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1000000007;
int n,k;
void icealsoheat(){cin>>n;string s;cin>>s;for(int i=1;i<n;i++){if(s.substr(0,i)<s.substr(i)){puts("Yes");return;}}puts("No");}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;cin>>_;while(_--){icealsoheat();}}B - Favorite Game
第二题也比较基础,我们可以先把后面的数组排序,然后枚举每一段(每一段的长度为k,包含按顺序的k个数)
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1000000007;
int n,k;
int b[1000005];
void icealsoheat(){int le,re;cin>>n>>k;cin>>le>>re;n-=2;int an=0;for(int i=1;i<=n;i++){cin>>b[i];if(b[i]>=le&&b[i]<=re)an++;}sort(b+1,b+1+n);if(an>=k){cout<<0;return;}int ans=0x3f3f3f3f3f3f3f3f;for(int i=1;i<=n-k+1;i++){int xx=0;if(le>b[i])xx+=abs(le-b[i]);if(re<b[i+k-1])xx+=abs(re-b[i+k-1]);ans=min(ans,xx);}cout<<ans;
}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;// cin>>_;while(_--){icealsoheat();}}C - Harmonic Mean
这题想到了裂项相消公式,但是没有想到给他们分开。
当存在n=t*(t+1)的时候,我们不能直接用数列(2,6,12,20.。。。。(n-1)*n,n)
而是把后n-1项看成一部分,使后n-1项的和等于1,然后把每一个项数*2,此时的后n-1项的总和为1/2,这时候我们只需要再放入一个2即可
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
const int MX=0x3f3f3f3f3f3f3f3f;
int n,k;
map<int,int>hh;
void yu(){for(int i=1;i<=500;i++){hh[i*(i+1)]=1;}
}
void icealsoheat(){cin>>n;if(n==2)cout<<"No\n";else{cout<<"Yes\n";if(n==1)cout<<"1\n";else if(n==3)cout<<"2 3 6\n";else{vector<int>ans;if(hh[n]){n--;for(int i=1;i<n;i++){ans.push_back(2ll*i*(i+1ll));}ans.push_back(2ll*n);cout<<"2 ";for(auto i:ans){cout<<i<<" ";}}else{for(int i=1;i<n;i++){cout<<i*(i+1)<<" ";}cout<<n;}cout<<"\n";}}}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;yu();cin>>_;while(_--){icealsoheat();}
}D - Sum of SCC

好厉害的题,开拓了我的视野。不看题解我是真想不到竟然还能这么dp。
我们可以知道,统计SSG(强连通分量)是很难统计的。竞赛图有一个性质:当我们把强连通分量缩点之后,拉直,整个竞赛图会变成一条很长的链,并且,长的链上的任何两个点之间都有一个链(很抽象又很神奇的想法)。既然变成了一个长长的链,那么其实我们可以通过在长链上某点进行一刀切,使其分成左右两个集合,分别是集合A与集合B,同时,我们定义集合A的所有点都与集合B的相连。且集合A的数字较小,集合B的数字较大。
我们用三维dp i,j,k来进行动态规划。i表示我们只有前i个点儿的状态,j表示A集合中有j个点儿,k表示有k条小数向大数连的边。
我们每次塞进去第i个点儿,有两种情况:
1.将该点儿塞入集合A中,那么该点儿可以从集合A中选择p个点使这p个点儿指向该点儿。
dp[i+1][j+1][k+p]+=dp[i][j][k]*c[j][p]
2.将该点儿塞入集合B中,那么A点都会指向该点儿,同时我们可以选取B集合中p个点儿,使其指向该点儿。
dp[i+1][j][j+k+p]+=dp[i][j][k]*c[i-j][p]
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int mod=998244353;
int n,m;
int c[505][505];void init(int mx)
{for(int i=0;i<=mx;i++)for(int j=0;j<=i;j++) c[i][j]=j?(c[i-1][j-1]+c[i-1][j])%mod:1;
}void icealsoheat(){cin>>n>>m;vector dp(50,vector(50,vector<int>(1600,0)));dp[0][0][0]=1;for(int i=0;i<n;i++){for(int j=0;j<=i;j++){for(int k=0;k<=i*(i-1)/2;k++){for(int p=0;p<=j;p++)(dp[i+1][j+1][k+p]+=dp[i][j][k]*c[j][p]%mod)%mod;for(int p=0;p<=i-j;p++)(dp[i+1][j][j+k+p]+=dp[i][j][k]*c[i-j][p]%mod)%mod;}}}int ans=0;for(int i=1;i<=n;i++){ans=(ans+dp[n][i][m])%mod;}cout<<ans;
}
signed main(){ios::sync_with_stdio(false);cin.tie();cout.tie();int _;_=1;// cin>>_;init(500);while(_--){icealsoheat();}}相关文章:

AC修炼计划(AtCoder Regular Contest 163)
传送门:AtCoder Regular Contest 163 - AtCoder 第一题我们只需要将字符串分成两段,如果存在前面一段比后面一段大就成立。 #include<bits/stdc.h> #define int long long using namespace std; typedef long long ll; typedef pair<int,int&g…...

持续进化,快速转录,Faster-Whisper对视频进行双语字幕转录实践(Python3.10)
Faster-Whisper是Whisper开源后的第三方进化版本,它对原始的 Whisper 模型结构进行了改进和优化。这包括减少模型的层数、减少参数量、简化模型结构等,从而减少了计算量和内存消耗,提高了推理速度,与此同时,Faster-Whi…...
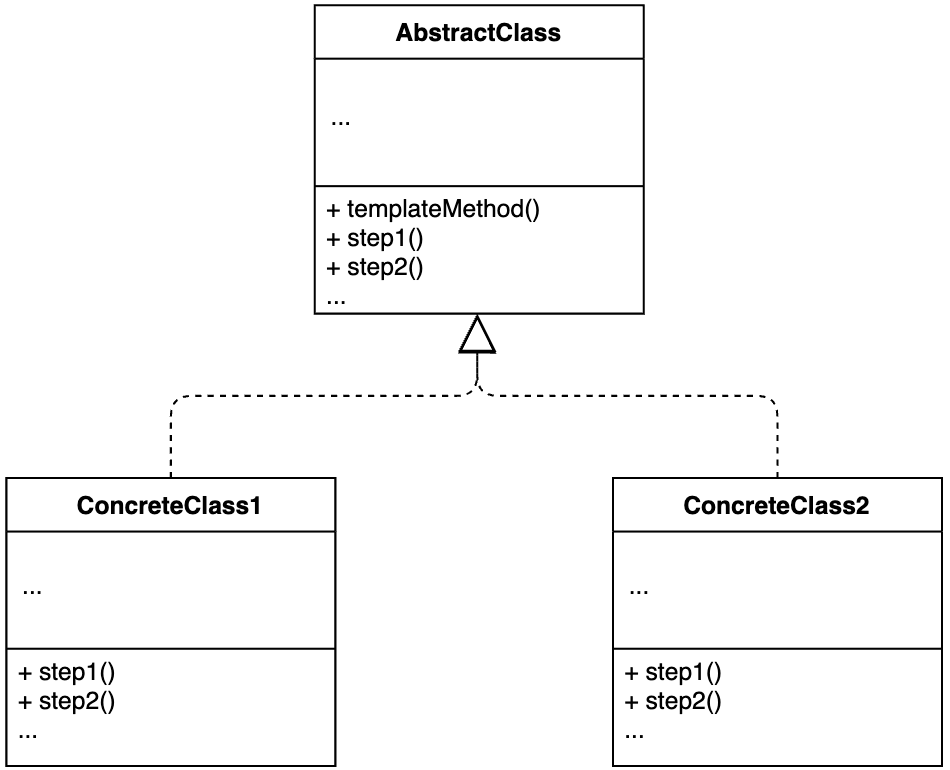
【设计模式】第24节:行为型模式之“模板方法模式”
一、简介 模板方法模式在一个方法中定义一个算法骨架,并将某些步骤推迟到子类中实现。模板方法模式可以让子类在不改变算法整体结构的情况下,重新定义算法中的某些步骤。 模板模式有两大作用:复用和扩展。其中,复用指的是&#…...
| 线代及概率论部分)
【考研数学】数学“背诵手册”(二)| 线代及概率论部分
文章目录 引言二、线代施密特正交化分块矩阵转置、逆、伴随之间的运算关于秩定义性质 三、概统常见分布的期望及方差 引言 这数一全部内容太多了,放在一篇文章里的话,要编辑就很困难,就把线代和概率放在这篇文章里吧。 二、线代 施密特正交…...
)
Android WMS——WindowState介绍(十三)
前面文章中的 addWindow 方法,首先获取了 DisplayContent,紧接着判断窗口的 type 类型并标记。然后获取 token 信息,且该信息是通过 DisplayContent 中的方法获取的。最后就是创建并保存 WindowState 信息。 一、简介 在窗口管理系统(Window Manager Service,WMS)中,Wi…...
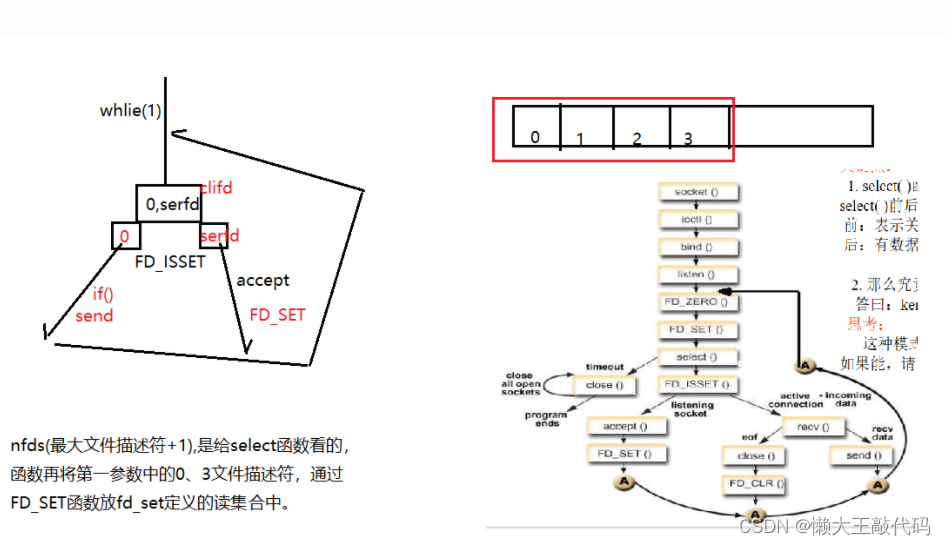
C/C++网络编程基础知识超详细讲解第二部分(系统性学习day12)
懒大王感谢大家的关注和三连支持~ 目录 前言 一、UDP编程 UDP特点: UDP框架: UDP函数学习 发送端代码案例如下: 二、多路复用 前提讲述 select poll 三、图解如下 总结 前言 作者简介: 懒大王敲代码,…...

【教3妹学编程-算法题】117. 填充每个节点的下一个右侧节点指针 II
2哥 : 3妹,听说你昨天去面试了,怎么样啊? 3妹:嗨,别提了,让我回去等通知,估计是没有通知了, 还浪费我请了一天假。 2哥 : 你又请假了啊, 你是怎么跟你那个严厉的老板请假…...
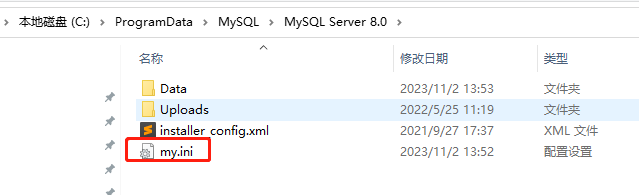
window10 mysql8.0 修改端口port不生效
mysql的默认端口是3306,我想修改成3307。 查了一下资料,基本上都是说先进入C:\Program Files\MySQL\MySQL Server 8.0这个目录。 看看有没有my.ini,没有就新建。 我这里没有,就新建一个,然后修改port: […...
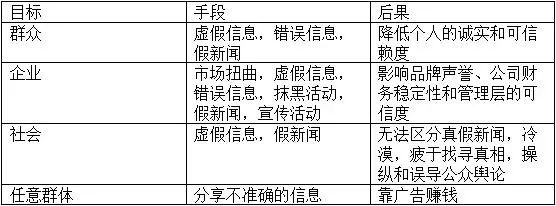
欧盟网络安全威胁:虚假与错误信息
如今,数字平台已是新闻媒体的主战地。社交网站、新闻媒体、甚至搜索引擎都是现在大多数人的信息来源。由于这些网站的运作方式是通过吸引人们来产生网站流量,这些抓人眼球的信息通常是推广广告,有些甚至没有经过审查。 国际现状 恶意攻击者现…...
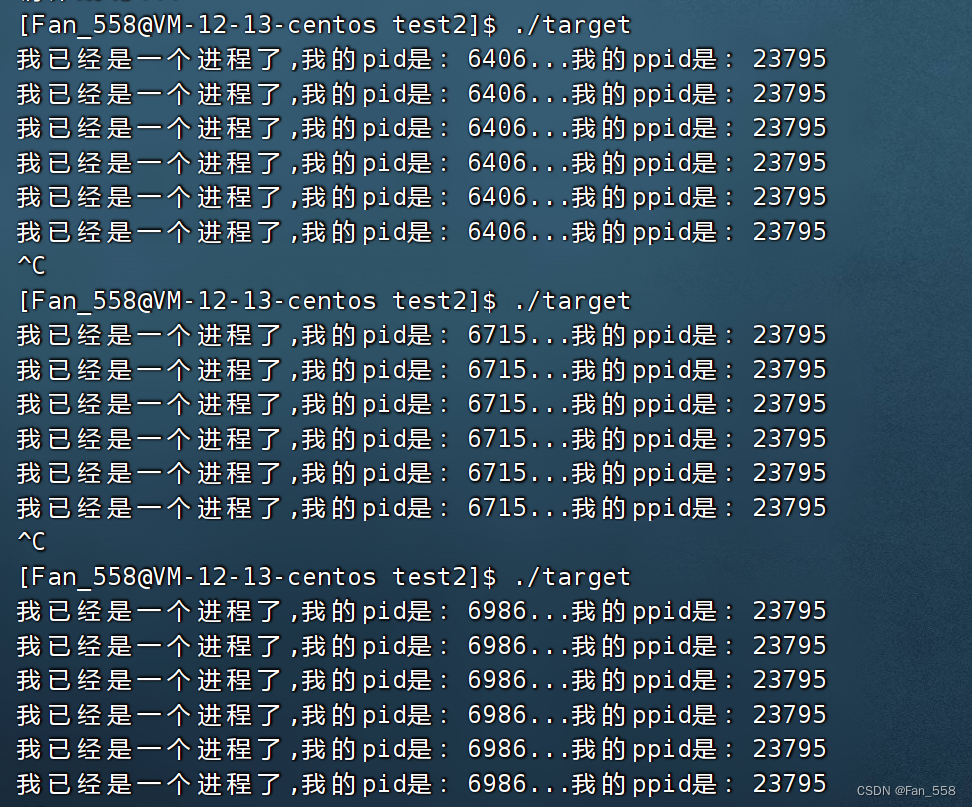
006 Linux 进程的概念 | 获取进程的PID
前言 本文将会向您进程的概念,程序与进程的区别,如何获取进程的标识符-pid 文章重点 1.描述进程——PCB 进程与程序的区别 CPU对进程列表的处理 2.获取进程PID 描述进程-PCB 进程概念 课本概念:程序的一个执行实例或正在执行的程序 内核…...
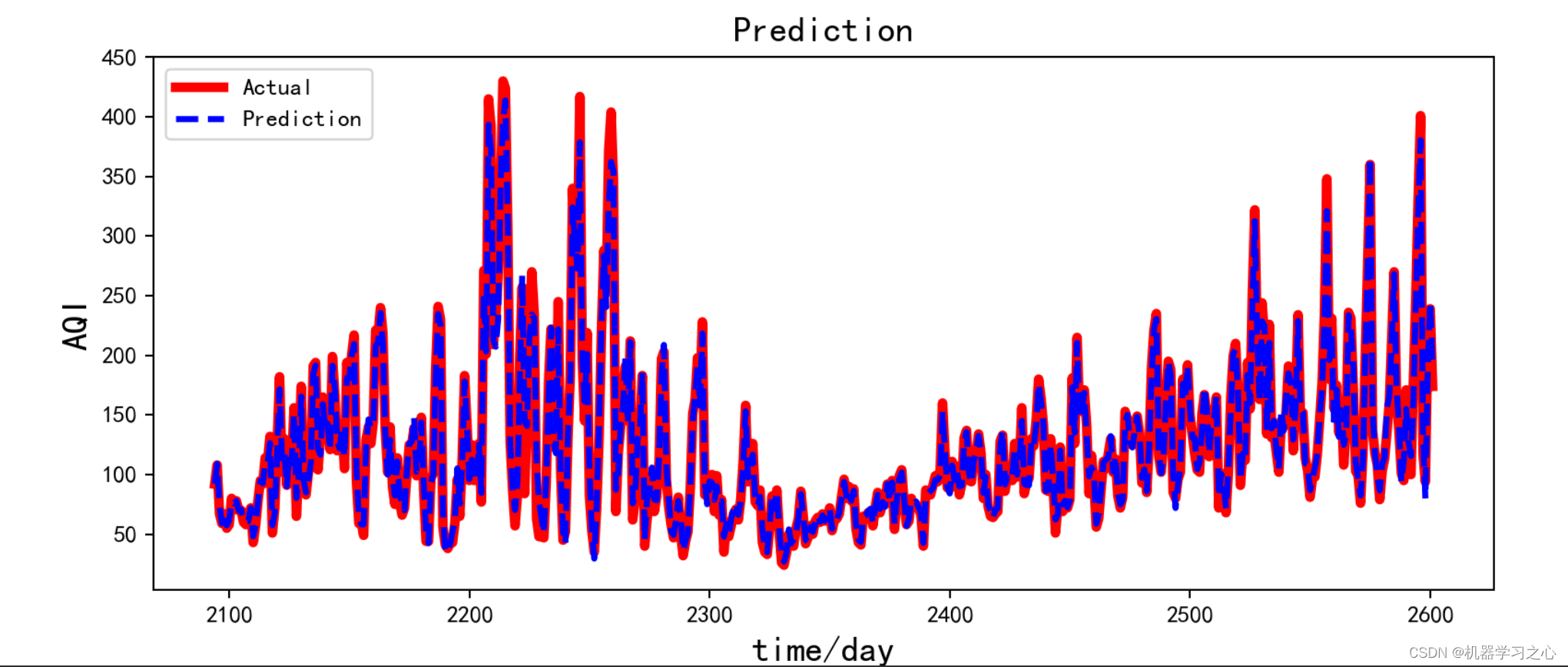
时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测
时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测 目录 时序预测 | Python实现ARIMA-CNN-LSTM差分自回归移动平均模型结合卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 时序预测 …...

《异常检测——从经典算法到深度学习》23 TimesNet: 用于常规时间序列分析的时间二维变化模型
zz# 《异常检测——从经典算法到深度学习》 0 概论1 基于隔离森林的异常检测算法 2 基于LOF的异常检测算法3 基于One-Class SVM的异常检测算法4 基于高斯概率密度异常检测算法5 Opprentice——异常检测经典算法最终篇6 基于重构概率的 VAE 异常检测7 基于条件VAE异常检测8 Don…...
)
计算机网络(59)
1. OSI 的七层模型分别是?各自的功能是什么? 2. 为什么需要三次握手?两次不行? 3. 为什么需要四次挥手?三次不行? 4. TCP与UDP有哪些区别?各自应用场景? 5. HTTP1.0,1.1&…...
【CSS】CSS基础知识扫盲
1、 什么是CSS? CSS即层叠样式表 (Cascading Style Sheets). CSS 能够对网页中元素位置的排版进行像素级精确控制, 实现美化页面的效果. 能够做到页面的样式和结构分离 2、 CSS引入方式 CSS代码编写的时候有多种引入方式: 内部样式、外部样式、内联样…...

React中的状态管理
目录 前言 1. React中的状态管理 1.1 本地状态管理 1.2 全局状态管理 Redux React Context 2. React状态管理的优势 总结 前言 当谈到前端开发中的状态管理时,React是一个备受推崇的选择。React的状态管理机制被广泛应用于构建大型、复杂的应用程序…...

【优选算法系列】【专题九链表】第一节.链表常用技巧和操作总结(2. 两数相加)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、链表常用技巧和操作总结二、两数相加 2.1 题目描述 2.2 题目解析 2.2.1 算法原理 2.2.2 代码编写总结 前言 一、链表常…...
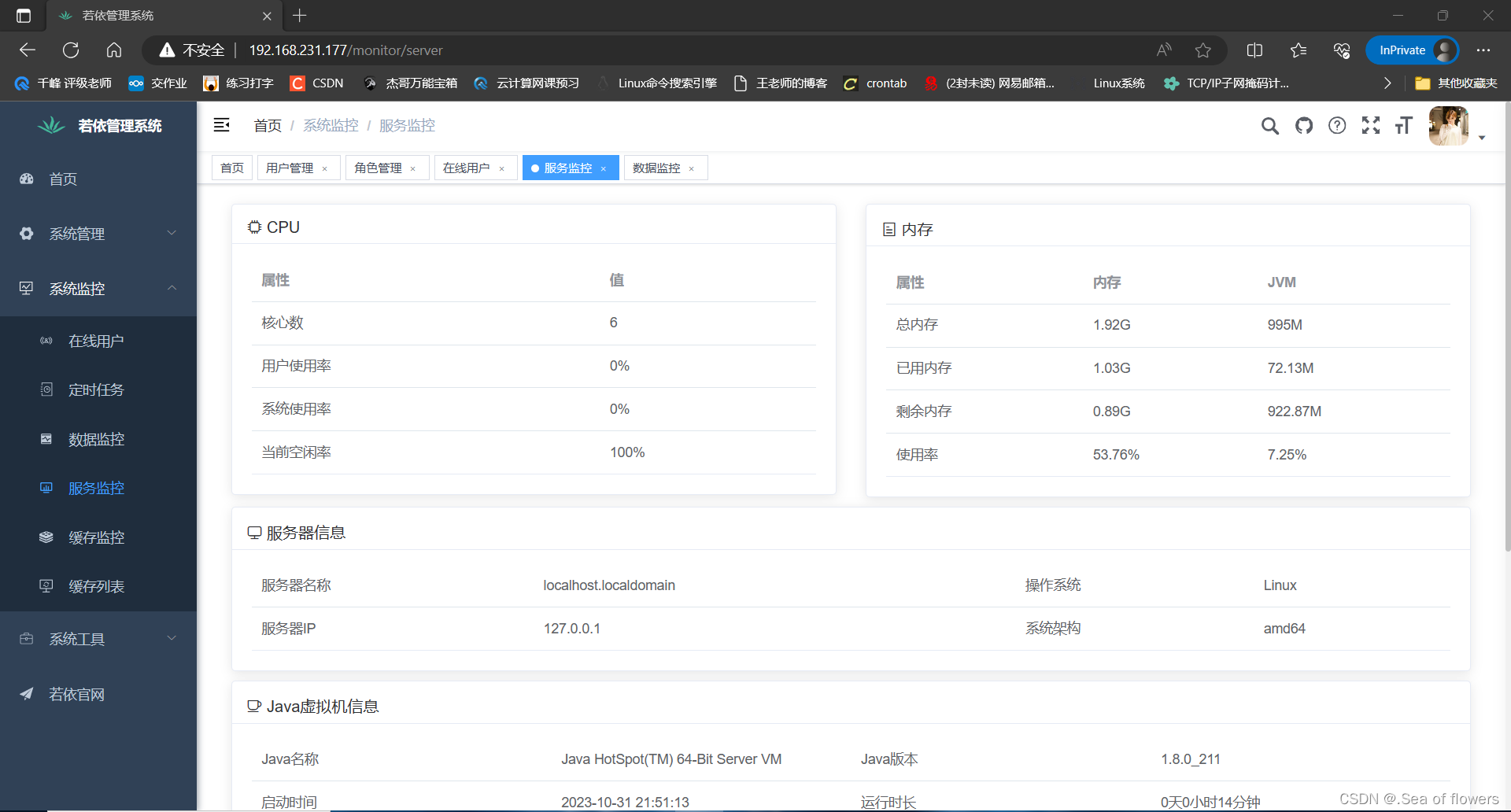
上线Spring boot-若依项目
基础环境 所有环境皆关闭防火墙与selinux 服务器功能主机IP主机名服务名称配置前端服务器192.168.231.177nginxnginx1C2G后端服务器代码打包192.168.231.178javajava、maven、nodejs4C8G数据库/缓存192.168.231.179dbmysql、redis2C4G Nginx #配置Nginxyum源 [rootnginx ~]…...
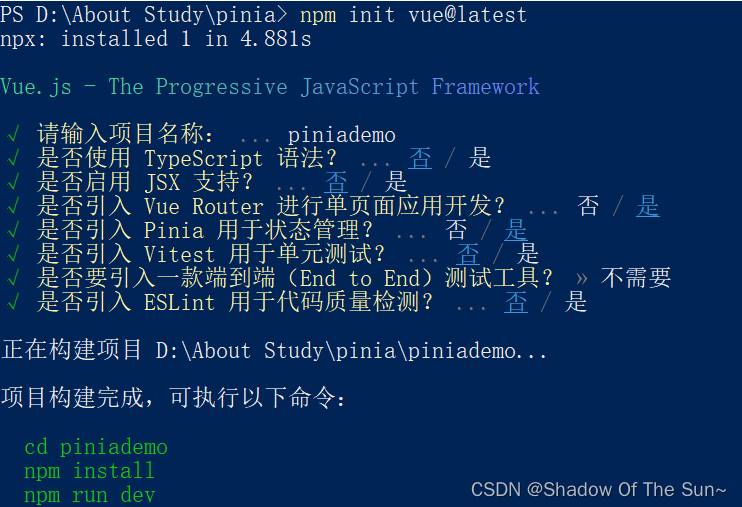
pinia简单使用
新命令-创建vue3项目 vue create 方式使用脚手架创建项目,vue cli处理, vue3后新的脚手架工具create-vue 使用npm init vuelatest 命令创建即可。 在pinia中,将使用的组合式函数识别为状态管理内容 自动将ref 识别为stste,computed 相当于 ge…...
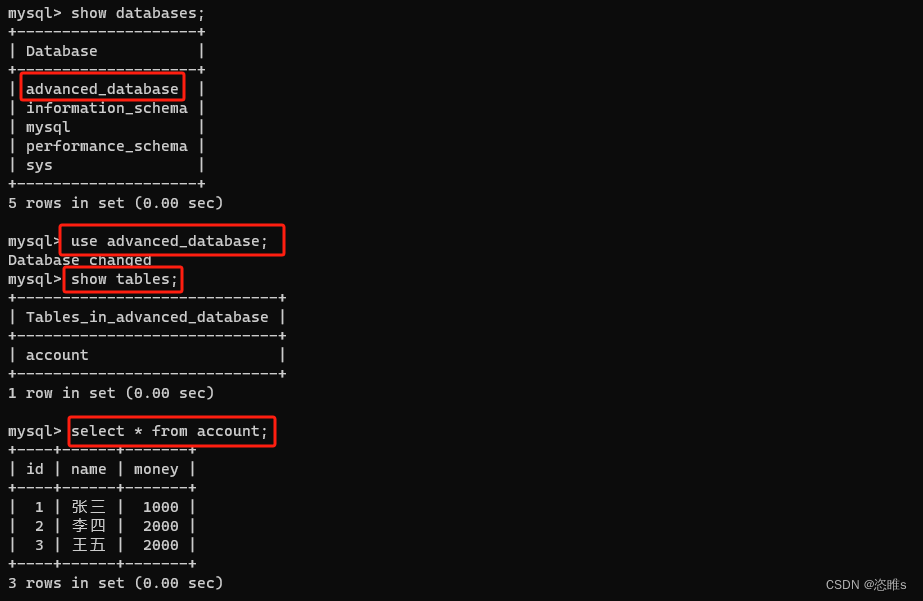
数据库进阶教学——数据库故障恢复(日志文件)
目录 一、日志简介 二、日志文件操作 1、查看日志状态 2、开启日志功能 3、查看日志文件 4、查看当前日志 5、查看日志中的事件 6、删除日志文件 7、查看和修改日志文件有效期 8、查看日志文件详细信息 三、删除的数据库恢复 一、日志简介 日志是记录所有数据库表结…...
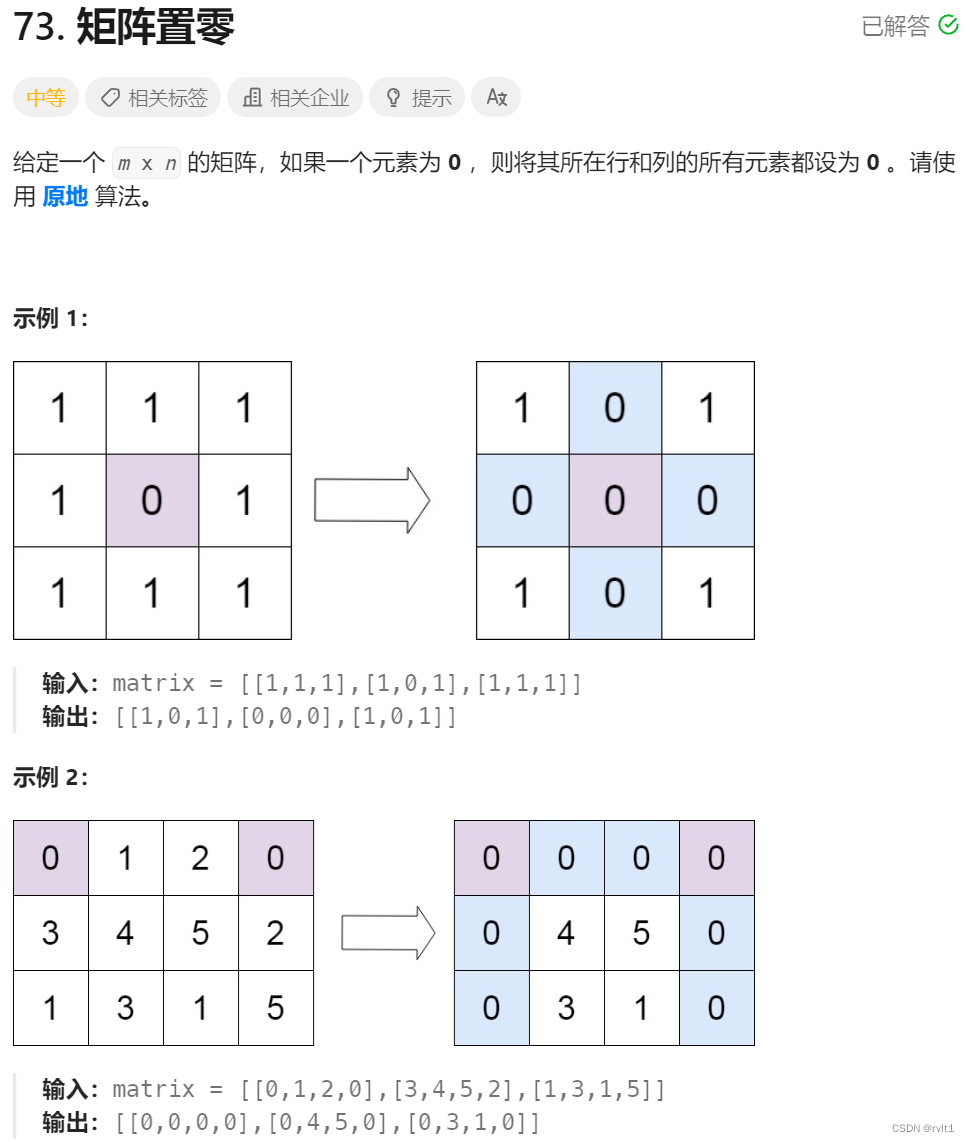
Leetcode 73 矩阵置0
class Solution {//1.用矩阵的第一行和第一列来标记该行或该列是否应该为0,但是这样的话忽视了第一行或第一列为0的情况//2.用标记row0和column0来标记第一行或第一列是否该为0public void setZeroes(int[][] matrix) {int n matrix.length;int m matrix[0].length;boolean r…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
