代码随想录算法训练营第23期day39 |62.不同路径、63. 不同路径 II
目录
一、(leetcode 62)不同路径
1.动态规划
1)确定dp数组(dp table)以及下标的含义
2)确定递推公式
3)dp数组的初始化
4)确定遍历顺序
5)举例推导dp数组
2.数论方法
二、(leetcode 63)不同路径 II
一、(leetcode 62)不同路径
力扣题目链接
1.动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1)确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2)确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
3)dp数组的初始化
首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
4)确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
5)举例推导dp数组
如图所示:
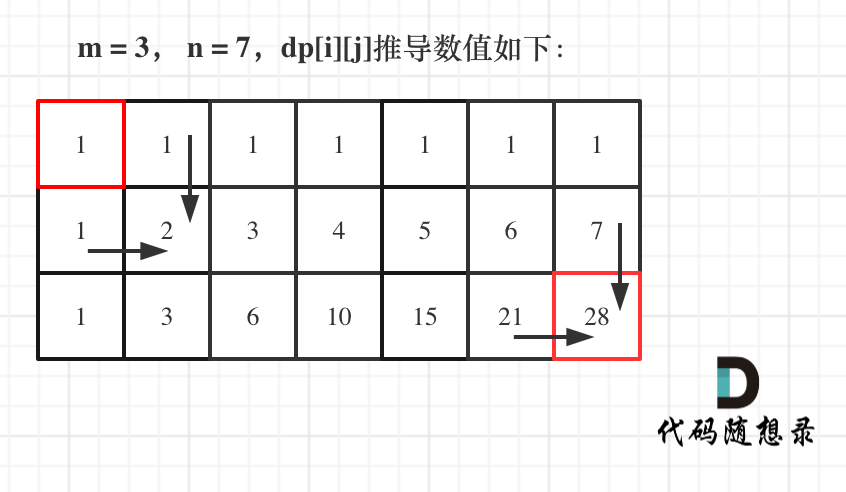
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(m × n)
其实用一个一维数组(也可以理解是滚动数组)就可以了,但是不利于理解,可以优化点空间,建议先理解了二维,在理解一维,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {dp[i] += dp[i - 1];}}return dp[n - 1];}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(n)
2.数论方法
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
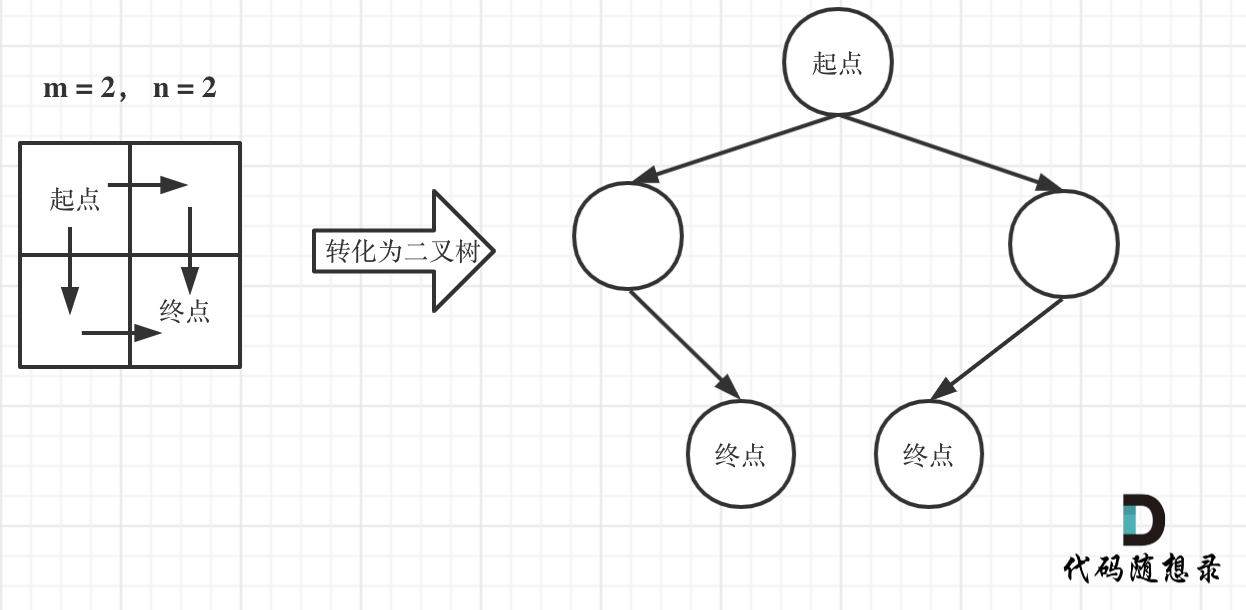
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
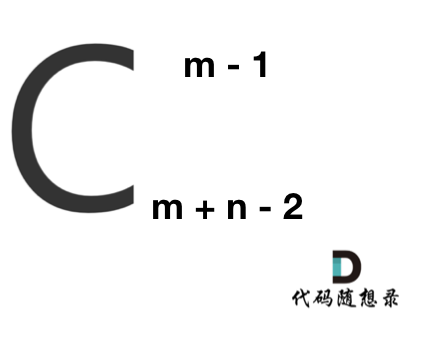
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
class Solution {
public:int uniquePaths(int m, int n) {int numerator = 1, denominator = 1;int count = m - 1;int t = m + n - 2;while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母return numerator / denominator;}
};需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; // 分子int denominator = m - 1; // 分母int count = m - 1;int t = m + n - 2;while (count--) {numerator *= (t--);while (denominator != 0 && numerator % denominator == 0) {numerator /= denominator;denominator--;}}return numerator;}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
二、(leetcode 63)不同路径 II
力扣题目链接
有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了
动规五部曲:
1)确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2)确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
3)dp数组如何初始化
在62.不同路径 (opens new window)不同路径中我们给出如下的初始化:
vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
如图:
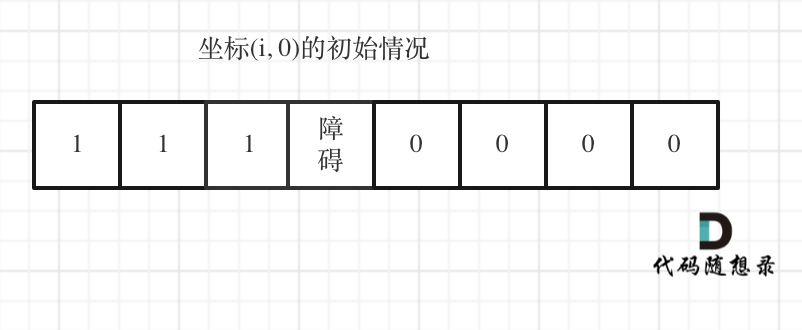
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
4)确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}
5)举例推导dp数组
拿示例1来举例如题:
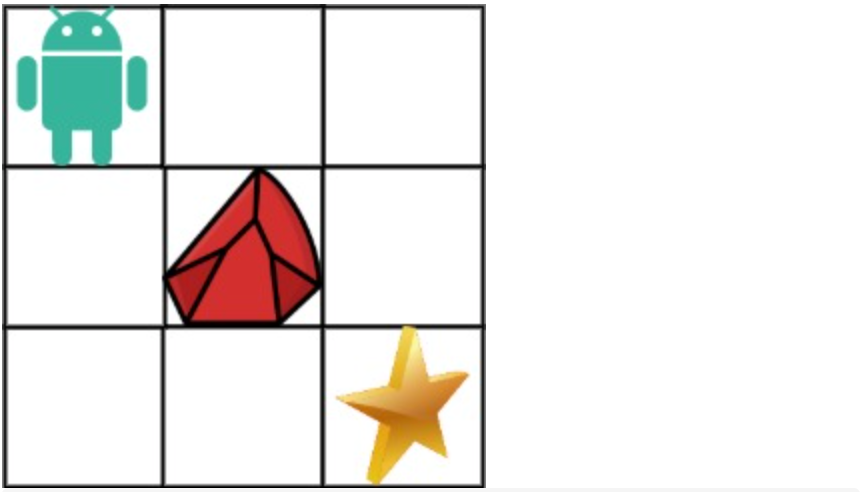
对应的dp table 如图:
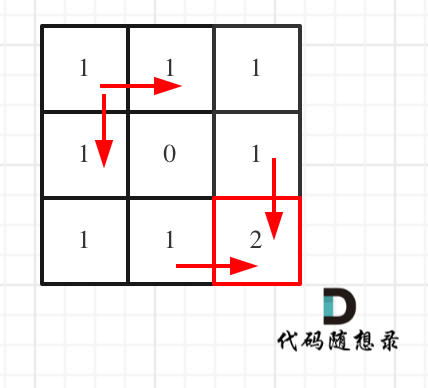
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
动规五部分分析完毕,对应C++代码如下:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(n × m)
同样给出空间优化版本:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {if (obstacleGrid[0][0] == 1)return 0;vector<int> dp(obstacleGrid[0].size());for (int j = 0; j < dp.size(); ++j)if (obstacleGrid[0][j] == 1)dp[j] = 0;else if (j == 0)dp[j] = 1;elsedp[j] = dp[j-1];for (int i = 1; i < obstacleGrid.size(); ++i)for (int j = 0; j < dp.size(); ++j){if (obstacleGrid[i][j] == 1)dp[j] = 0;else if (j != 0)dp[j] = dp[j] + dp[j-1];}return dp.back();}
};- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(m)
相关文章:

代码随想录算法训练营第23期day39 |62.不同路径、63. 不同路径 II
目录 一、(leetcode 62)不同路径 1.动态规划 1)确定dp数组(dp table)以及下标的含义 2)确定递推公式 3)dp数组的初始化 4)确定遍历顺序 5)举例推导dp数组 2.数论方…...

白帽黑客入门,“每天一个黑客技巧”实现黑客的自我突破 !(附工具包!)
年底了,不少朋友都是在总结一年的学习成果。最后发现完成情况与自己最初定下的目标相去甚远。 同时也针对粉丝和网上大部分存在的问题进行了整理: “为什么我感觉学安全好难?” “渗透测试到底该怎么学?” “为什么总是挖不到漏…...
Jmeter参数化 —— 循环断言多方法
1、参数化接口测试数据 注意:csv文档参数化,里面有多少条数据,就要在线程组里循环多少次,不然就只执行一次 2、添加配置元件-计数器 关于计数器 ①Starting Value:给定计数器的初始值; ②递增:每次循环迭代…...
要点及配置开发详解)
Autosar诊断实战系列26-Dem(DTCEvent)要点及配置开发详解
本文框架 前言1. Dem及其与其他模块交互介绍1.1 与DCM模块交互1.1.1 0x14服务调用时序1.1.2 0x85服务调用时序1.1.3 0x19服务调用时序1.2 与Fim模块交互1.3 与NvM模块交互1.4 与BswM模块交互1.5 与其他BSW及APP模块交互2. Dem配置开发介绍2.1 DemGeneral配置2.1.1 DemGeneral一…...
:queue)
STL(第五课):queue
STL(标准模板库)是一种C标准库,在其中包含了许多常用的数据结构和算法。其中,queue就是STL库中的一个数据结构,用于实现队列(先进先出FIFO)。 使用STL queue,需要引入头文件<queu…...
点大商城V2版 2.5.2.1 全开源独立版 多小程序端+unipp安装教程
点大商城V2是一款采用全新界面设计支持多端覆盖的小程序应用,支持H5、微信公众号、微信小程序、头条小程序、支付宝小程序、百度小程序,本程序是点大商城V2独立版,包含全部插件,代码全开源,并且有VUE全端代码。分销&am…...

Redo Log(重做日志)的刷盘策略
1. 概述 Redo Log(重做日志)是 InnoDB 存储引擎中的一种关键组件,用于保障数据库事务的持久性和崩溃恢复。InnoDB 将事务所做的更改先记录到重做日志,之后再将其应用到磁盘上的数据页。 刷盘策略(Flush Policy&#x…...

QT窗体之间值的传递,多种方法实现
目录 1. 信号和槽机制 2. 全局变量或单例模式 3. 事件过滤器 4. Qt属性系统 5. 使用QSettings类 在Qt中,有多种方法可以在窗体之间传递值。下面是一些常用的方法: 1. 信号和槽机制 使用Qt的信号和槽机制是一种常见的方式来在窗体之间传递值。您可以…...

政务服务技能竞赛中用到的软件和硬件
政务服务技能竞赛包括争上游、抢先机、秀风采、比擂台几个环节,用到选手端平板、评委端平板、主持人平板、抢答器等设备、抢答器等。分别计算团队分和个人分。答题规则和计分方案均较为复杂,一般竞赛软件无法实现,要用到高端竞赛软件…...
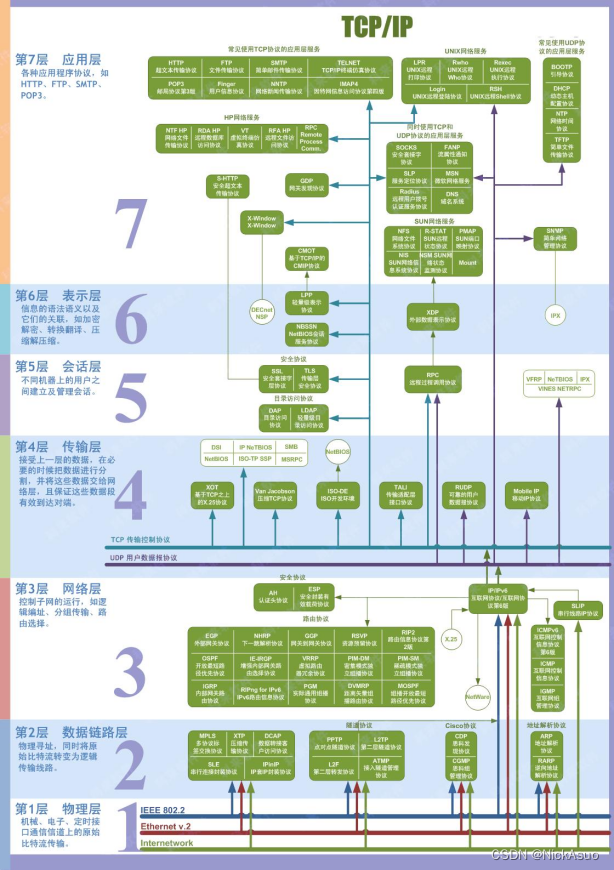
tcp/ip该来的还是得来
1. TCP/IP、Http、Socket的区别 \qquad 区别是:TCP/IP即传输控制/网络协议,也叫作网络通讯协议,它是在网络的使用中的最基本的通信协议。Http是一个简单的请求-响应协议,它通常运行在TCP之上。Socket是对网络中不同主机上的应用进…...

OpenCV官方教程中文版 —— 图像修复
OpenCV官方教程中文版 —— 图像修复 前言一、基础二、代码三、更多资源 前言 本节我们将要学习: • 使用修补技术去除老照片中小的噪音和划痕 • 使用 OpenCV 中与修补技术相关的函数 一、基础 在我们每个人的家中可能都会几张退化的老照片,有时候…...

前端难学还是后端难学?系统安全,web安全,网络安全是什么区别?
系统安全,web安全,网络安全是什么区别?三无纬度安全问题 系统安全,可以说是电脑软件的安全问题,比如windows经常提示修复漏洞,是一个安全问题 网页安全,网站安全,比如,…...
diffusers-Load pipelines,models,and schedulers
https://huggingface.co/docs/diffusers/using-diffusers/loadinghttps://huggingface.co/docs/diffusers/using-diffusers/loading 有一种简便的方法用于推理是至关重要的。扩散系统通常由多个组件组成,如parameterized model、tokenizers和schedulers,…...

私域营销必备:轻松掌握微信CRM管理方法
大家在微信私域营销中都遇到了什么问题? 比如管理时间不够,群发实效性低,自动回复无法适应变化等等。 我们可以利用微信CRM这个工具,轻松解决这些问题。 请问你们最想用这个工具解决什么问题呢? 使用微信CRM不仅可…...

最长回文子串-LeetCode5 动态规划
由于基础还不是很牢固 一时间只能想到暴力的解法: 取遍每个子串 总数量nn-1n-2…1 O(n^2) 判断每个子串是否属于回文串 O(n) 故总时间复杂度为O(n^3) class Solution { public:string longestPalindrome(string s) { int max0;string ret;for(int i0;i<s.size();i)for(int…...

mysql简单备份和恢复
版本:mysql8.0 官方文档 :MySQL :: MySQL 8.0 Reference Manual :: 7 Backup and Recovery 1.物理备份恢复 物理备份是以数据文件形式备份。这种方式效率高点,适合大型数据库备份。物理备份可冷备可热备。 使用mysqlbackup 命令进行物理备…...

JMeter介绍
1. JMeter是什么? 是Apache组织开发基于Java的接口测试工具,性能测试工具 2.JMeter的优缺点 优点: 开源,免费 跨平台 支持多协议 轻量级别 缺点: 不支持IP欺骗 不可验证页面UI 3.JMeter可以用来做什么? …...

flink job同时使用BroadcastProcessFunction和KeyedBroadcastProcessFunction例子
背景: 广播状态可以用于规则表或者配置表的实时更新,本文就是用一个欺诈检测的flink作业作为例子看一下BroadcastProcessFunction和KeyedBroadcastProcessFunction的使用 BroadcastProcessFunction和KeyedBroadcastProcessFunction的使用 1.首先看主流…...

数据中心系统解决方案
设计思路 系统设计过程中充分考虑各个子系统的信息共享要求,对各子系统进行结构化和标准化设计,通过系统间的各种联动方式将其整合成一个有机的整体,使之成为一套整体的、全方位的数据中心大楼综合管理系统,达到人防、物防和技防…...
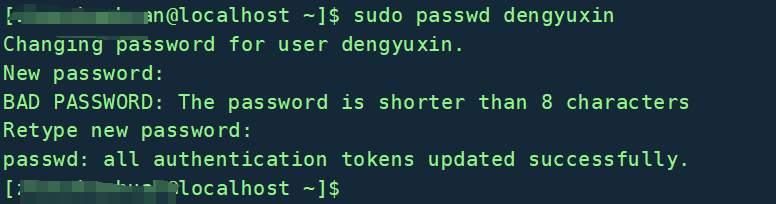
服务器开设新账户,创建账号并设置密码
实验室又进新同学了,服务器开设新账号搞起来 1、创建用户: 在root权限下,输入命令useradd -m 用户名,如下 sudo useradd -m yonghuming 2、设置密码: 输入命令passwd 用户名 回车,接着输入密码操作&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
