【Java|golang】2103. 环和杆---位运算
总计有 n 个环,环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。
给你一个长度为 2n 的字符串 rings ,表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ,用于描述每个环:
第 i 对中的 第一个 字符表示第 i 个环的 颜色(‘R’、‘G’、‘B’)。
第 i 对中的 第二个 字符表示第 i 个环的 位置,也就是位于哪根杆上(‘0’ 到 ‘9’)。
例如,“R3G2B1” 表示:共有 n == 3 个环,红色的环在编号为 3 的杆上,绿色的环在编号为 2 的杆上,蓝色的环在编号为 1 的杆上。
找出所有集齐 全部三种颜色 环的杆,并返回这种杆的数量。
示例 1:
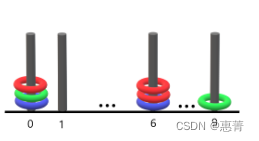
输入:rings = “B0B6G0R6R0R6G9”
输出:1
解释:
- 编号 0 的杆上有 3 个环,集齐全部颜色:红、绿、蓝。
- 编号 6 的杆上有 3 个环,但只有红、蓝两种颜色。
- 编号 9 的杆上只有 1 个绿色环。
因此,集齐全部三种颜色环的杆的数目为 1 。
示例 2:
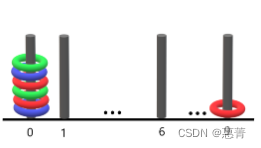
输入:rings = “B0R0G0R9R0B0G0”
输出:1
解释:
- 编号 0 的杆上有 6 个环,集齐全部颜色:红、绿、蓝。
- 编号 9 的杆上只有 1 个红色环。
因此,集齐全部三种颜色环的杆的数目为 1 。
示例 3:
输入:rings = “G4”
输出:0
解释:
只给了一个环,因此,不存在集齐全部三种颜色环的杆。
提示:
rings.length == 2 * n
1 <= n <= 100
如 i 是 偶数 ,则 rings[i] 的值可以取 ‘R’、‘G’ 或 ‘B’(下标从 0 开始计数)
如 i 是 奇数 ,则 rings[i] 的值可以取 ‘0’ 到 ‘9’ 中的一个数字(下标从 0 开始计数)
public int countPoints(String rings) {int[] ints = new int[10];int res=0;for (int i = 0; i < rings.length(); i+=2) {int j = rings.charAt(i + 1) - '0';ints[j]|=rings.charAt(i)=='R'?1:rings.charAt(i)=='G'?2:4;if (ints[j]==7){res++;ints[j]=ints[j]<<1;}}return res;}

func countPoints(rings string) int {ints:=[10]int{}res:=0for i := 0; i < len(rings); i+=2 {j := rings[i + 1] - '0'if rings[i]=='R' {ints[j]|=1}else if rings[i]=='G' {ints[j]|=2}else {ints[j]|=4}if ints[j]==7{res++ints[j]=ints[j]<<1}}return res
}

相关文章:

【Java|golang】2103. 环和杆---位运算
总计有 n 个环,环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。 给你一个长度为 2n 的字符串 rings ,表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ,用于描述每个环: 第 …...

[SSD综述 1.4] SSD固态硬盘的架构和功能导论
依公知及经验整理,原创保护,禁止转载。 专栏 《SSD入门到精通系列》 <<<< 返回总目录 <<<< 前言 机械硬盘的存储系统由于内部结构, 其IO访问性能无法进一步提高,CPU与存储器之间的性能差距逐渐扩大。以Nand Flash为存储介质的固态硬盘技术的发展,…...

【C++那些事儿】类与对象(1)
君兮_的个人主页 即使走的再远,也勿忘启程时的初心 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,我之前看过一套书叫做《明朝那些事儿》,把本来枯燥的历史讲的生动有趣。而C作为一门接近底层的语言,无疑是抽象且难度颇…...
集简云x slack(自建)无需API开发轻松连接OA、电商、营销、CRM、用户运营、推广、客服等近千款系统
slack是一个工作效率管理平台,让每个人都能够使用无代码自动化和 AI 功能,还可以无缝连接搜索和知识共享,并确保团队保持联系和参与。在世界各地,Slack 不仅受到公司的信任,同时也是人们偏好使用的平台。 官网&#x…...

JS模块化,ESM模块规范的 导入、导出、引用、调用详解
JS模块化,ESM模块规范的 导入、导出、引用、调用详解 写在前面实例代码1、模块导出 - export导出之 - 独立导出导出之 - 集中多个导出导出之 - 默认导出导出之 - 集中默认导出导出之 - 混合导出 2、模块导入 - import导入之 - 全部导入导入之 - 默认导入导入之 - 指…...

markdown常用的快捷键
一级标题 #加 空格 是一级标题 二级标题 ##加空格是二级标题 三级标题 字体 * 粗体:两个**号 斜体:一个 斜体加粗:三个 删除:两个~~ 我是字体 我是字体 我是字体 我是字体 引用 箭头符号>加空格 回车 分割线 三个 - …...
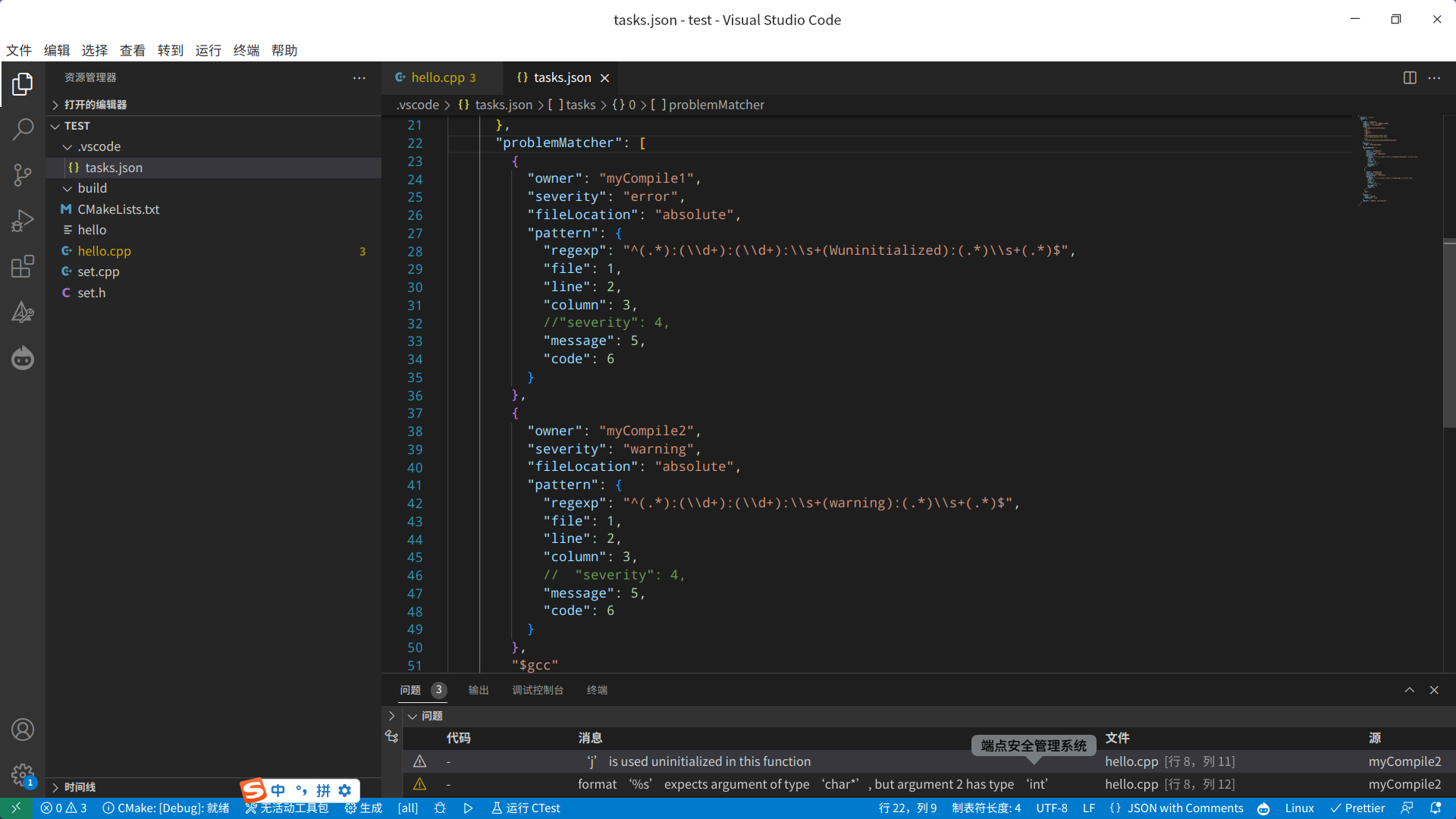
VSCode中的任务什么情况下需要配置多个问题匹配器problemMatcher?多个问题匹配器之间的关系是什么?
☞ ░ 前往老猿Python博客 ░ https://blog.csdn.net/LaoYuanPython 一、简介 在 VS Code 中,tasks.json 文件中的 problemMatcher 字段用于定义如何解析任务输出中的问题(错误、警告等)。 problemMatcher是一个描述问题匹配器的接口&…...

C语言鞍点数组改进版
题目内容: 给定一个n*n矩阵A。矩阵A的鞍点是一个位置(i,j),在该位置上的元素是第i行上的最大数,第j列上的最小数。一个矩阵A也可能没有鞍点。 你的任务是找出A的鞍点。 改进目标: 网络上很多…...
K8s:部署 CNI 网络组件+k8s 多master集群部署+负载均衡及Dashboard k8s仪表盘图像化展示
目录 1 部署 CNI 网络组件 1.1 部署 flannel 1.2 部署 Calico 1.3 部署 CoreDNS 2 负载均衡部署 3 部署 Dashboard 1 部署 CNI 网络组件 1.1 部署 flannel K8S 中 Pod 网络通信: ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容…...
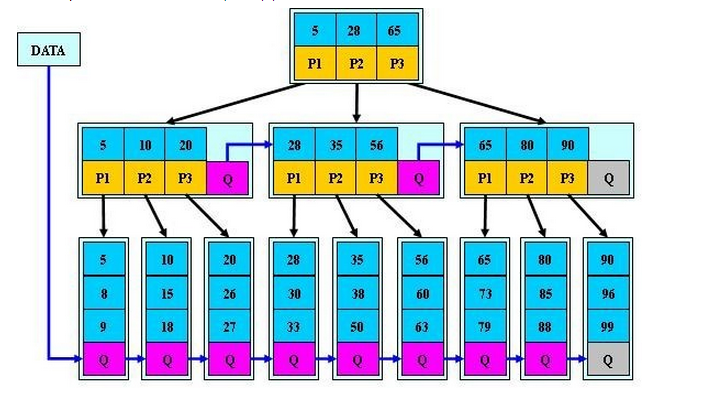
【数据结构】树家族
目录 树的相关术语树家族二叉树霍夫曼树二叉查找树 BST平衡二叉树 AVL红黑树伸展树替罪羊树 B树B树B* 树 当谈到数据结构中的树时,我们通常指的是一种分层的数据结构,它由节点(nodes)组成,这些节点之间以边(…...

Vert.x学习笔记-Vert.x的基本处理单元Verticle
Verticle介绍 Verticle是Vert.x的基本处理单元,Vert.x应用程序中存在着处理各种事件的处理单元,比如负责HTTP API响应请求的处理单元、负责数据库存取的处理单元、负责向第三方发送请求的处理单元。Verticle就是对这些功能单元的封装,Vertic…...
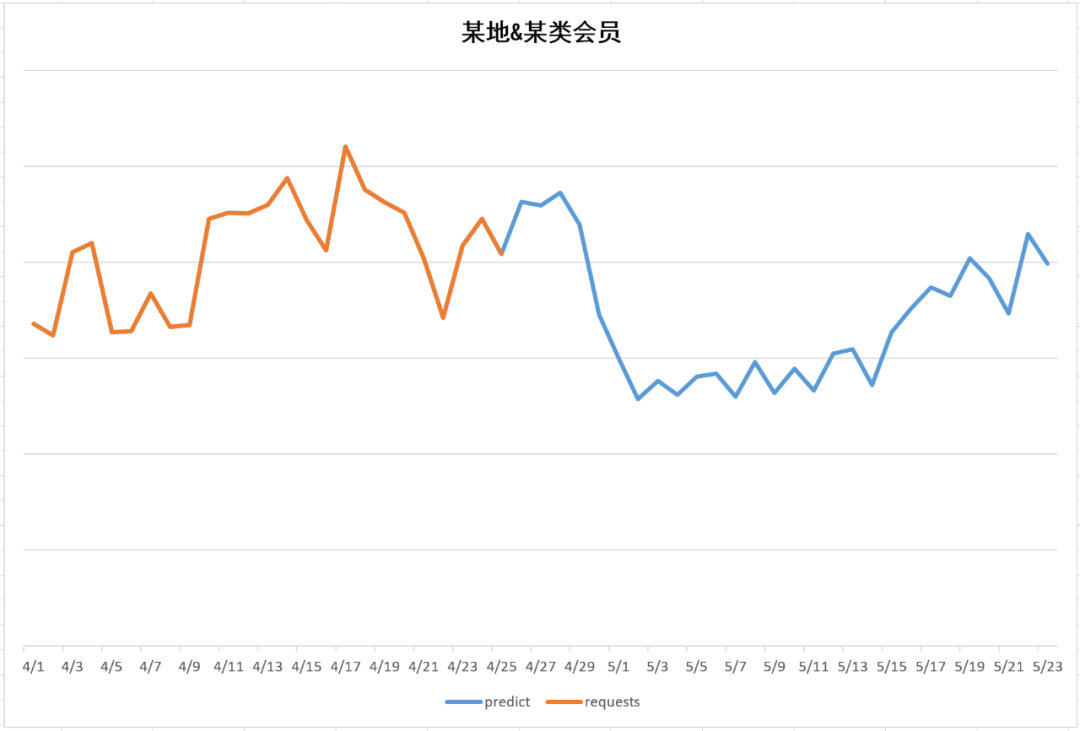
干货分享:基于 LSTM 的广告库存预估算法
近年来,随着互联网的发展,在线广告营销成为一种非常重要的商业模式。出于广告流量商业化售卖和日常业务投放精细化运营的目的,需要对广告流量进行更精准的预估,从而更精细的进行广告库存管理。 因此,携程广告纵横平台…...

dataframe删除某一列
drop import pandas as pd data {‘A’: [1, 2, 3], ‘B’: [4, 5, 6], ‘C’: [7, 8, 9]} df pd.DataFrame(data) #使用drop方法删除列 df df.drop(‘B’, axis1) # 通过指定列名和axis1来删除列 del import pandas as pd data {‘A’: [1, 2, 3], ‘B’: [4, 5, 6]…...

提升ChatGPT答案质量和准确性的方法Prompt engineering
文章目录 怎么获得优质的答案设计一个优质prompt的步骤:Prompt公式:示例怎么获得优质的答案 影响模型回答精确度的因素 我们应该知道一个好的提示词,要具备一下要点: 清晰简洁,不要有歧义; 有明确的任务/问题,任务如果太复杂,需要拆分成子任务分步完成; 确保prompt中…...
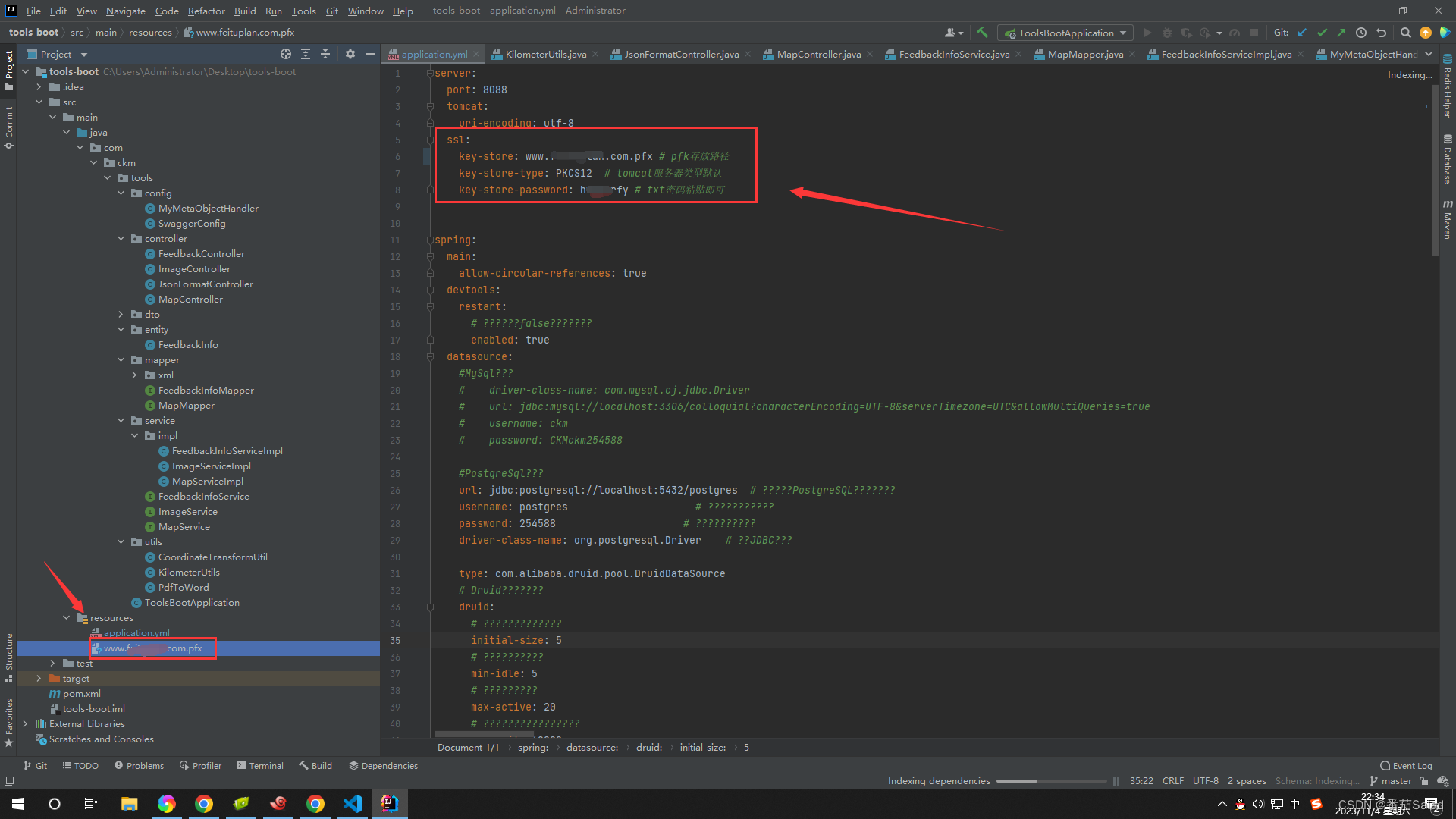
SpringBoot + Vue2项目打包部署到服务器后,使用Nginx配置SSL证书,配置访问HTTP协议转HTTPS协议
配置nginx.conf文件,这个文件一般在/etc/nginx/...中,由于每个人的体质不一样,也有可能在别的路径里,自己找找... # 配置工作进程的最大连接数 events {worker_connections 1024; }# 配置HTTP服务 http {# 导入mime.types配置文件…...

HTML 表格
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>表格标签</title>/* <style>.yun {widt…...
试用 10 -- 安全性问题)
AIGC(生成式AI)试用 10 -- 安全性问题
上次遗留的问题:代码的安全性呢?下次找几个问题测试下看。 AI,你安全吗? AI生成的程序,安全吗? 也许这个世界最难做的事就是自己测试自己:测试什么?如何测? …...
STM32循迹小车原理介绍和代码示例
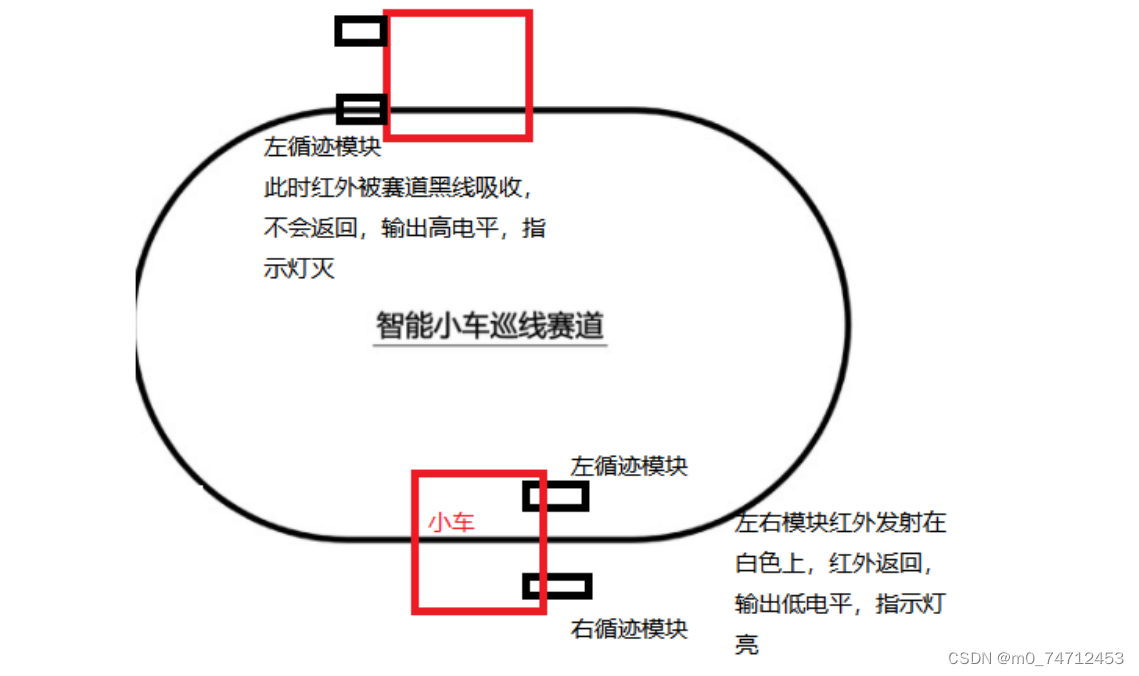
目录 1. 循迹模块介绍 2. 循迹小车原理 3. 循迹小车核心代码 4. 循迹小车解决转弯平滑问题 1. 循迹模块介绍 TCRT5000传感器的红外发射二极管不断发射红外线当发射出的红外线没有被反射回来或被反射回来但强度不够大时红外接收管一直处于关断状态,此时模块的输出…...

Nginx 配置详细讲解
Nginx.conf 配置文件分为三部分,分别为main块、events块、http块(http块又包含server块和location块),如下图。 第一部分:main块(全局块) main块主要是设置一些影响Nginx服务器整体运行的配置指令,主要包括…...
)
gdb 日志记录不显示到屏幕的方法(gdb13最新版)
tags: gdb categories: [Debug] 写在前面 gdb 的更新好快啊… 之前的选项都有改动了, 比如 logging… 需要屏幕重定向不能简单设置: set logging on set logging redirect on了, 而是要多开一个配置, 踩坑了 方法 在此之前先看一下我的 gdbinit 配置: set debuginfod e…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
