0-1矩阵列互斥问题——回溯法 Python实现
三、 0-1 矩阵的列集互斥问题。给定一个 m × n m \times n m×n 的 0-1 矩阵 A \mathrm{A} A 。定义列互斥为: 对于矩阵 A A A 中的任意两列 i i i 和 j j j, 如果在对应的每一行上, i i i 和 j j j 不存在同时为 1 的情况, 则称列 i \mathrm{i} i 和 j \mathrm{j} j 互斥。定义列集互斥为: 设 S 1 \mathrm{S} 1 S1 和 S 2 \mathrm{S} 2 S2 为矩阵 A \mathrm{A} A 中的列的集合, S 1 S1 S1 和 S 2 S2 S2 之间没有交集 (即, 不允许 A \mathrm{A} A 中的某列既属于 S 1 \mathrm{S} 1 S1 又属于 S 2 \mathrm{S} 2 S2 ), 如果在对应的每一行上, S 1 \mathrm{S} 1 S1 中的任意一列和 S 2 \mathrm{S} 2 S2 中的任意一列不存在同时为 1 的情况, 则称列集 S 1 \mathrm{S} 1 S1 和 S 2 S2 S2 互斥。设计一个算法, 求出 A \mathrm{A} A 上的一组 S 1 \mathrm{S} 1 S1 和 S 2 \mathrm{S} 2 S2 ,使得 S 1 \mathrm{S} 1 S1 和 S 2 \mathrm{S} 2 S2 包含的列的个数为最多
S 1 S1 S1和 S 2 S2 S2非空。
思路:

适当的利用剪枝函数和限界函数以减少搜索的空间:
- 剪枝函数:即题目要求,只有互斥才能进入下一层。
- 限界函数:目前A和B矩阵的列数加上剩余的列数已经小于当前最优解,放弃向下搜索。
使用Py编写这个算法的时候,可以使用numpy库的数据,加快我们运行的速度,同时可以减少很多循环遍历数组的冗余代码。
为了节省时间,我们在开始计算前,先把 n n n列向量的互斥关系都计算出来,保存在一个 n × n n \times n n×n的矩阵内。
import numpy as np
import matplotlib.pyplot as pltclass Matrix:def __init__(self, array):self.array = arrayrows, columns = array.shapeself.belong = np.zeros(columns, dtype=int) # 1属于A, 2属于Bself.solve = np.zeros(columns, dtype=int) # 最终解self.best = 0 # 最佳列数self.sumA = 0 # 记录当前A列数self.sumB = 0 # 记录当前B列数self.judge = np.ones((columns, columns), dtype=int) # 减少时间的关键,判断两列互斥self.diff = 9999# 先计算出列与列之间的互斥关系1代表不互斥,0代表互斥for i in range(columns):self.judge[i, i] = 0for j in range(i):for k in range(rows):if array[k, i] == 1 and array[k, j] == 1:self.judge[i, j] = 0self.judge[j, i] = 0break# j列能否归入Adef could_be_a(self, j):for i in range(j):if self.belong[i] == 2 and self.judge[i, j] == 0:return Falsereturn True# j列能否归入Bdef could_be_b(self, j):for i in range(j):if self.belong[i] == 1 and self.judge[i, j] == 0:return Falsereturn Truedef biggest_divide(self, i):columns = self.array.shape[1]if i >= columns:if self.sumA + self.sumB > self.best and self.sumA and self.sumB and np.abs(self.sumA-self.sumB) < self.diff:self.best = self.sumA + self.sumBself.solve = self.belong.copy()self.diff = np.abs(self.sumA-self.sumB)returnif self.could_be_a(i):self.belong[i] = 1self.sumA += 1self.biggest_divide(i + 1)self.belong[i] = 0self.sumA -= 1if self.could_be_b(i):self.belong[i] = 2self.sumB += 1self.biggest_divide(i + 1)self.belong[i] = 0self.sumB -= 1if self.sumA + self.sumB + columns - i >= self.best:self.biggest_divide(i + 1)def show(self):a_indices = np.where(self.solve == 1)[0]b_indices = np.where(self.solve == 2)[0]print("A:", a_indices)print("B:", b_indices)color_array = self.array.copy()color_array[:, a_indices] *= 10color_array[:, b_indices] *= 7plt.matshow(color_array, cmap=plt.cm.Reds)plt.show()row = 50
colume = 20
array = np.random.choice([0, 1], size=(row, colume), p=[0.8, 0.2])
test = Matrix(array)
test.biggest_divide(0)
test.show()
使用show来可视化最终结果,如果这里只取列数合最大,一般A列都比较多,如果要好看的结果可以限制A列和B列之间距离越小越好,多设置一个diff参数,当列数合相同时,保存A列与B列相差较小的结果。
在 m m m=50, n n n=20下,1填充率为20%,随机填充下的互斥结果,深红色为A集合,鲜红色为B集合。
A: [ 0 5 16 17 19]
B: [ 2 7]

时间复杂度分析:
- 对于每一列,回溯算法会考虑三种可能性:将其归入 A 部分或归入 B 部分或者不归入。
- 对于每一列的三种可能性,又会递归考虑下一列的三种可能性,以此类推。
- 这样的递归结构导致了指数级的搜索树。
- 在最坏情况下,需要考虑的列数等于矩阵的列数,因此有 3 n 3^n 3n种可能性,其中 n n n 是列数。
相关文章:

0-1矩阵列互斥问题——回溯法 Python实现
三、 0-1 矩阵的列集互斥问题。给定一个 m n m \times n mn 的 0-1 矩阵 A \mathrm{A} A 。定义列互斥为: 对于矩阵 A A A 中的任意两列 i i i 和 j j j, 如果在对应的每一行上, i i i 和 j j j 不存在同时为 1 的情况, 则称列 i \mathrm{i} i 和 j \mathrm{j} j 互斥…...
wandb 安装本地部署使用教程
1、官网注册 wandb.ai是一个为机器学习开发者提供的开发工具平台,可以帮助用户跟踪实验,管理和版本数据,以及与团队协作,从而更专注于构建最佳模型。 wandb官网: https://wandb.ai 首先我们打开官网注册号自己的账号并…...

飞桨平台搭建PP-YOLOE模型
一、创建项目 此博客仅是运行PP-YOLOE源码,这里以变压器渗漏数据集为例COCO数据集太大了,跑不动,V100训练预估计得7天左右,即便是A100也得4天半,变压器渗漏油数据集跑一个小时左右,还可以接受,…...

Js重点内容
一,什么是js javascript是运行在客户端(浏览器,可预览)的编程语言 二,主要的功能 用来给静态页(html网页)增加一些动态功能(比如轮播图、tab切换) 三,应用…...
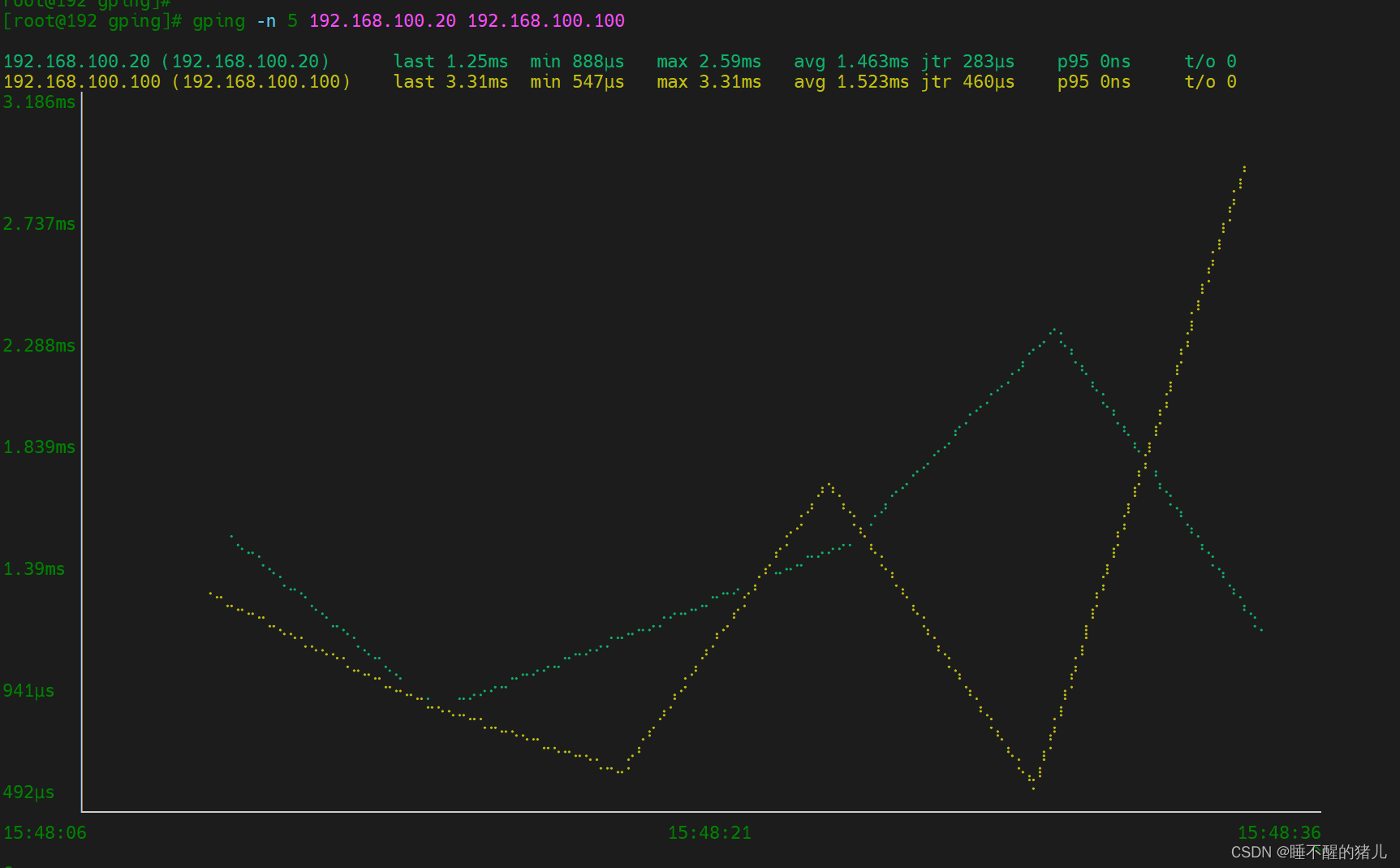
图形化ping工具gping
一、介绍 gping能够以折线图的方式,实时展示 ping 的结果,支持 Windows、Linux 和 macOS 操作系统。并且支持多个目标同时Ping同时展示折线图方便对比。下面扩展一下ICMP及ICMP隧道。 ICMP消息结构: ICMP消息是由一个类型字段、一个代码字段、…...
快速安装虚拟机centos7.5
vbox 快速导入安装centos7.5 环境准备 vbox安装(下载地址) ova镜像(下载地址)(默认是192.168.56.10 加nat网卡) 链接:https://pan.baidu.com/s/164Iprh_80HCQmKCU6V-RTw 提取码:if…...

2023.11.4 Idea 配置国内 Maven 源
目录 配置国内 Maven 源 重新下载 jar 包 配置国内 Maven 源 <mirror><id>alimaven</id><name>aliyun maven</name><url>http://maven.aliyun.com/nexus/content/groups/public/</url><mirrorOf>central</mirrorOf> …...

DAY11 字符串处理函数
1.测字符串长度函数 头文件: #include <string.h> 函数定义: size_t strlen(const char *s); 函数功能: 测字符指针 s 指向的字符串中字符的个数,不包括 ’\0’ void fun01() {char *num "hello";int len …...

Web自动化测试 —— PageObject设计模式!
一、page object 模式简介 1.1、传统 UI 自动化的问题 无法适应 UI 频繁变化无法清晰表达业务用例场景大量的样板代码 driver/find/click 二、page object 设计原则 2.1、POM 模式的优势 降低 UI 变化导致的测试用例脆弱性问题让用例清晰明朗,与具体实现无关 2.…...

七月论文审稿GPT第2版:从Meta Nougat、GPT4审稿到Mistral、LongLora
前言 如此前这篇文章《学术论文GPT的源码解读与微调:从chatpaper、gpt_academic到七月论文审稿GPT》中的第三部分所述,对于论文的摘要/总结、对话、翻译、语法检查而言,市面上的学术论文GPT的效果虽暂未有多好,可至少还过得去&am…...
—— 日夜交替)
Unreal Engine 学习笔记 (1)—— 日夜交替
1.创建关卡 文件新建关卡空白关卡保存关卡(命名为NewWorld) 2.创建蓝图类 创建蓝图类(继承自Actor) 命名为SunAndMoon 3.编辑SunAndMoon蓝图类 添加SkyAtmosphere添加SkyLight添加DirectionalLight将DirectionalLight重命名为…...
leetcode:189. 轮转数组(python3解法)
难度:中等 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4]解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3…...
基于PHP + MySQL实现的文章内容管理系统源码+数据库,采用前后端分离的模板和标签化方式
文章内容管理系统 dc-article是一个通用的文章内容管理系统,基于开源的caozha-admin开发,采用前后端分离的模板和标签化方式,支持文章内容管理、栏目分类管理、评论管理、友情链接管理、碎片管理、远程图片获取器等功能。可以使用本系统很轻…...
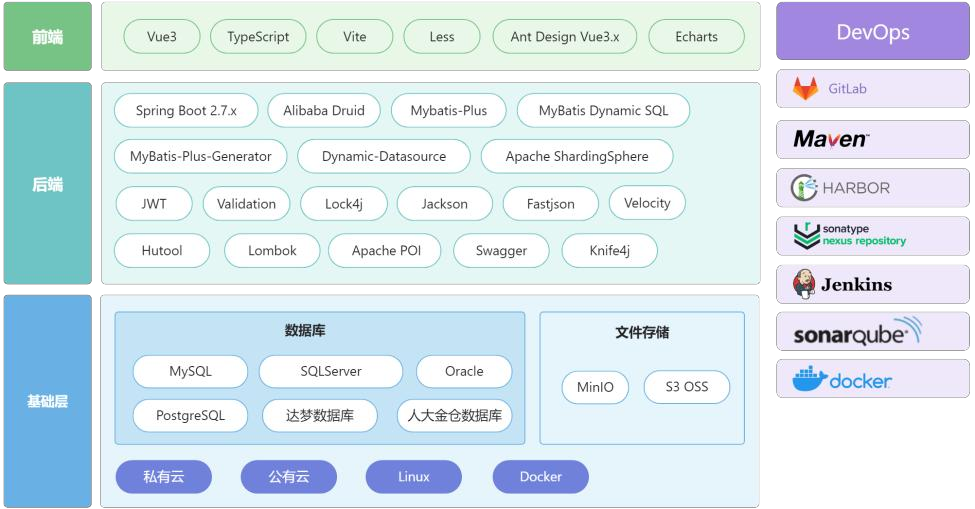
这可能是全网最晚的低代码技术总结
低代码的发展一向结伴着质疑前行,一些人认为低代码平台限制了开发人员的创新能力,使得开发过程变得过于简单,缺乏深度的定制和灵活性。他们担心,低代码平台可能只适合于简单的应用程序,无法满足复杂业务需求。另一面&a…...

leetcode2054
leetcode 2054 #include <iostream> #include <vector> #include <tuple> #include <algorithm>using namespace std;struct Event {// 时间戳int ts;// op 0 表示左边界,op 1 表示右边界int op;int val;Event(int _ts, int _op, int _v…...
c面向对象编码风格(上)
面向对象和面向过程的基本概念 面向对象和面向过程是两种不同的编程范式,它们在软件开发中用于组织和设计代码的方式。 面向过程编程(Procedural Programming)是一种以过程(函数、方法)为核心的编程方式。在面向过程…...
)
【星海出品】VUE(六)
插槽Slots 传递属性 attribute App,vue <script> import SlotsBase from "./components/SlotsBase.vue" import SlotsTow from "./components/SlotsTow.vue" export default {components:{SlotsBase,SlotsTow},data(){return{message: "父集 m…...

华为政企闪存存储产品集
产品类型产品型号产品说明 maintainProductOceanStor Dorado 2000 SAS 128GB华为OceanStor Dorado 2000是一款简单、可靠、绿色的全闪存存储系统,极简部署、智能运维、轻量便捷,功能齐全,广泛适用于虚拟化、数据库、办公自动化、分支机构等…...

【项目源码】反编译Java字节码生成源码
【项目源码】反编译Java字节码生成源码 文章目录 【项目源码】反编译Java字节码生成源码参考资料一、什么是反编译?二、反编译Java字节码文件1. (不一定有效) 使用IDEA提供的插件 - Java Bytecode Decomplier2. (推荐)…...

技术分享 | 测试人员必须掌握的测试用例
测试用例(Test Case)是为特定的目的而设计的一组测试输入、执行条件和预期结果的文档。它的作用其实就是为了测试是否满足某个特定需求。测试用例是指导测试工作进行的依据。 测试用例的组成 标准的测试用例通常由以下几个模块组成: 用例编…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
