Leetcode Daily Challenge 1845. Seat Reservation Manager
1845. Seat Reservation Manager
题目要求:初始化一个SeatManager类包括默认构造函数和类函数,所有的seat初始化为true。reverse函数返回最小的true,然后把这个编号的椅子赋值为false。unreverse(seatNumber)函数把编号为seatNumber的椅子恢复成true。
思路
本来想用常规的循环,每次reverse就搜索最小值,时间复杂度是O(n*m),会超时。因此考虑采用优先队列,每次会自动排序,队列的top就是可用的最小值,用完之后pop()。如果unreverse则把seatNumber push到优先队列中。
class SeatManager {
public:priority_queue<int, vector<int>, greater<int>> availableSeats;SeatManager(int n) {for (int seatNumber = 1; seatNumber <= n; ++seatNumber) {availableSeats.push(seatNumber);}}int reserve() {int seatNumber = availableSeats.top();availableSeats.pop();return seatNumber;}void unreserve(int seatNumber) {availableSeats.push(seatNumber);}
};/*** Your SeatManager object will be instantiated and called as such:* SeatManager* obj = new SeatManager(n);* int param_1 = obj->reserve();* obj->unreserve(seatNumber);*/

相关文章:

Leetcode Daily Challenge 1845. Seat Reservation Manager
1845. Seat Reservation Manager 题目要求:初始化一个SeatManager类包括默认构造函数和类函数,所有的seat初始化为true。reverse函数返回最小的true,然后把这个编号的椅子赋值为false。unreverse(seatNumber)函数把编号为seatNumber的椅子恢…...

Blender vs 3ds Max:谁才是3D软件的未来
在不断发展的3D建模和动画领域,两大软件巨头Blender和3ds Max一直在争夺顶级地位。 随着技术的进步和用户需求的演变,一个重要问题逐渐浮出水面:Blender是否最终会取代3ds Max?本文将深入探讨二者各自的优势和劣势、当前状况&…...
MapReduce:大数据处理的范式
一、介绍 在当今的数字时代,生成和收集的数据量正以前所未有的速度增长。这种数据的爆炸式增长催生了大数据领域,传统的数据处理方法往往不足。MapReduce是一个编程模型和相关框架,已成为应对大数据处理挑战的强大解决方案。本文探讨了MapRed…...
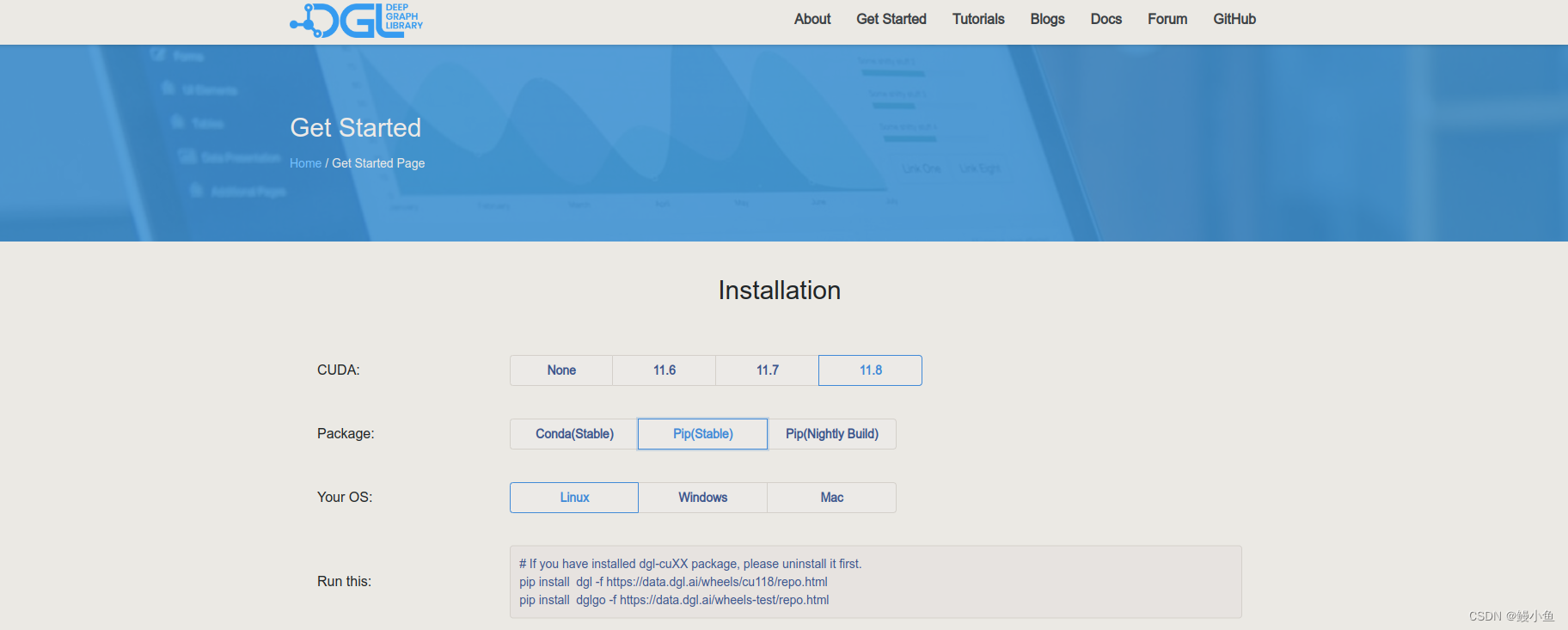
【已解决】ModuleNotFoundError: No module named ‘dgl‘
禁止使用下面方法安装DGL,这种方法会更新你的pytorch版本,环境越变越乱 pip install dgl 二是进入DGL官网:Deep Graph Library (dgl.ai),了解自己的配置情况,比如我cuda11.8,ubuntu,当然和linux是一样的 …...

R 复习 菜鸟教程
R语言老师说R好就业,学就完了 基础语法 cat()可以拼接函数: > cat(1, "加", 1, "等于", 2, \n) 1 加 1 等于 2sink():重定向 sink("r_test.txt", splitTRUE) # 控制台同样输出 for (i in 1:5) print(i…...

第十二章《搞懂算法:朴素贝叶斯是怎么回事》笔记
朴素贝叶斯是经典的机器学习算法,也是统计模型中的一个基本方法。它的基本思想是利用统计学中的条件概率来进行分类。它是一种有监督学习算法,其中“朴素”是指该算法基于样本特征之间相互独立这个“朴素”假设。朴素贝叶斯原理简单、容易实现࿰…...

【从0到1开发一个网关】网关Mock功能的实现
文章目录 什么是Mock?如何实现Mock什么是Mock? Mock(模拟)是一种测试技术,用于创建虚拟对象来模拟真实对象的行为。Mock对象模拟了真实对象的行为,但是不依赖于真实对象的实现细节。它们可以在测试中替代真实对象,以便进行独立的单元测试。 需要使用Mock的原因包括以下几…...

前端框架Vue学习 ——(三)Vue生命周期
生命周期:指一个对象从创建到销毁的整个过程。 生命周期的八个阶段:每触发一个生命周期事件,会自动执行一个生命周期方法(钩子) mounted:挂载完成,Vue 初始化成功,HTML 页面渲染成功…...
相机滤镜软件Nevercenter CameraBag Photo mac中文版特点介绍
Nevercenter CameraBag Photo mac是一款相机和滤镜应用程序,它提供了一系列先进的滤镜、调整工具和预设,可以帮助用户快速地优化和编辑照片。 Nevercenter CameraBag Photo mac软件特点介绍 1. 滤镜:Nevercenter CameraBag Photo提供了超过2…...

游戏专用....
游戏专用:星际战甲 APP窗口以及键鼠监控 import tkinter as tk import time,threading from pynput.keyboard import Key,Listener import pynput.keyboard as kbclass myClass:def __init__(self):self.root tk.Tk()self.new_text self.flag threading.Event()…...

第三方登录和第三方支付
第三方登录 在现代Web应用中,提供第三方登录选项已经变得非常普遍。用户可以使用其社交媒体或其他在线帐户(如Google、GitHub或Facebook)来访问您的应用程序,而无需创建新的用户名和密码。这提供了更好的用户体验,减少…...

SpringMvc执行流程(含过滤器Filter+拦截器interceptor)
目录 1.Mvc的概念 2.SpringMvc的概念 3.SpringMvc的核心组件 4.SpringMvc的执行流程 5.SpringMvcFilterInterceptor执行流程 一、Mvc的概念 Mvc(Model View Controller):Mvc是一种设计规范,它将数据、视图、业务逻辑代码进行分离,降低代码…...
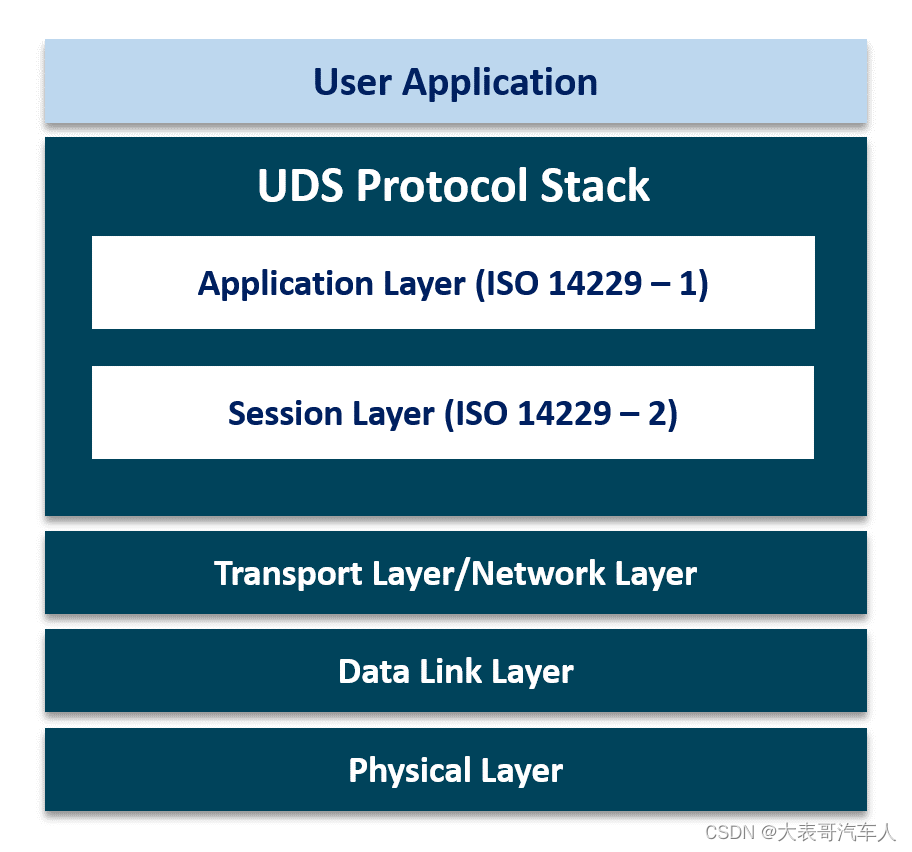
【UDS基础】简单介绍“统一诊断服务“
1. 前言 我们将在这个实用教程中介绍UDS的基础知识,重点关注在CAN总线上的UDS(UDSonCAN)和CAN诊断(DoCAN)。此外,我们还会介绍ISO-TP协议,并解释UDS、OBD2、WWH-OBD和OBDonUDS之间的差异。 最后,我们将解释如何请求、记录和解码UDS消息,并提供一些实际示例,例如记录…...
深度学习框架TensorFlow.NET之数据类型及张量2(C#)
环境搭建参考: 深度学习框架TensorFlow.NET环境搭建1(C#)-CSDN博客 由于本文作者水平有限,如有写得不对的地方,往指出 声明变量:tf.Variable 声明常量:tf.constant 下面通过代码的方式进行学…...

Pandas指定多列组合形成新列
目录 1、数据准备2、多列组合 1、数据准备 df pd.DataFrame({first_name: [A, B], last_name: [a, b]}) print(df.to_string()) first_name last_name 0 A a 1 B b 2、多列组合 2.1、方式一:使用cat() df[full_name] df[firs…...
硕鼠——视频下载利器
相信很多做自媒体、剪辑的同志们,经常会遇到一个棘手的问题:剪辑的素材从何而来。诸如很多高燃混剪的视频,往往需要多个影视作品中的原画来进行二次创作,可是这些视频素材从何而来呢? 有小伙伴们提出,通过录…...
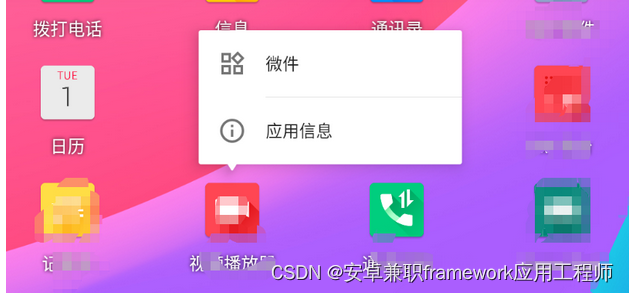
Android 13.0 Launcher3 app图标长按去掉应用信息按钮
1.前言 在13.0的rom定制化开发中,在Launcher3定制化开发中,对Launcher3的定制化功能中,在Launcher3的app列表页会在长按时,弹出微件和应用信息两个按钮,点击对应的按钮跳转到相关的功能页面, 现在由于产品需求要求禁用应用信息,不让进入到应用信息页面所以要去掉应用信息…...

10 DETR 论文精读【论文精读】End-to-End Object Detection with Transformers
目录 DETR 这篇论文,大家为什么喜欢它?为什么大家说它是一个目标检测里的里程碑式的工作?而且为什么说它是一个全新的架构? 1 题目 2摘要 2.1新的任务定义:把这个目标检测这个任务直接看成是一个集合预测的问题 2.…...
高数笔记05:不定积分与定积分
图源:文心一言 时间比较紧张,仅导图~~🥝🥝 第1版:查资料、画导图~🧩🧩 参考资料:《高等数学 基础篇》武忠祥 🐳目录 🐳目录 🐳不定积分 &#…...

【代码随想录】算法训练计划13
1、347. 前 K 个高频元素 题目: 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2] 思路: sort.Slice学习一下,其实还有so…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
