LeetCode|动态规划|392. 判断子序列、115. 不同的子序列、 583. 两个字符串的删除操作
目录
一、392. 判断子序列
1.题目描述
2.解题思路
3.代码实现(双指针解法)
4.代码实现(动态规划解法)
二、115. 不同的子序列
1.题目描述
2.解题思路
3.代码实现(C语言版本)
4.代码实现(C++版本)
三、583. 两个字符串的删除操作
1.题目描述
2.解题思路
3.代码实现(C语言版本)
一、392. 判断子序列
1.题目描述
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
输入:s = "abc", t = "ahbgdc" 输出:true
示例 2:
输入:s = "axc", t = "ahbgdc" 输出:false
提示:
0 <= s.length <= 1000 <= t.length <= 10^4- 两个字符串都只由小写字符组成。
2.解题思路
1.双指针解法:这也是看到这个题目一开始想到的方法
- 指针p1指向s开头,指针p2指向t开头,分别判断是否相等,相等就p1++,p2++,否则就p2++
2.动态规划解法:判断这两个字符串数组,最长公共子序列长度是否==s.szie()
3.代码实现(双指针解法)
bool isSubsequence(char* s, char* t) {char* p1 = s;char* p2 = t;for(;*p1!='\0',*p2!='\0';){if(*p1==*p2){p1++;p2++;}else {p2++;}}if(*p1 == '\0')return true;return false;
}4.代码实现(动态规划解法)
bool isSubsequence(char* s, char* t) {//考虑用最长公共子序列求解//动态规划思路,如果最长公共子序列的长度是字符串s的长度,那么就return trueint slen = strlen(s);int tlen = strlen(t);//对于dp数组初始化int **dp = (int**)malloc(sizeof(int*)*(slen+1));for(int i = 0;i <= slen;i++){dp[i] = (int*)malloc(sizeof(int) * (tlen+1));for(int j = 0;j <= tlen;j++){dp[i][j] = 0;}}for(int i = 1;i <= slen;i++){for(int j = 1;j<=tlen;j++){if(s[i-1]==t[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = dp[i][j-1];}}}int result = dp[slen][tlen];for(int i = 0;i <= slen;i++){free(dp[i]);}free(dp);if(result == slen) return true;else return false;
}二、115. 不同的子序列
1.题目描述
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例 1:
输入:s = "rabbbit", t = "rabbit"输出:3解释: 如下所示, 有 3 种可以从 s 中得到"rabbit" 的方案。rabbbitrabbbitrabbbit
示例 2:
输入:s = "babgbag", t = "bag"输出:5解释: 如下所示, 有 5 种可以从 s 中得到"bag" 的方案。babgbagbabgbagbabgbagbabgbagbabgbag
2.解题思路
- 动态规划解法,dp数组含义:以i-1结尾的s中,含有以j-1结尾的t的个数为dp[i][j]
3.代码实现(C语言版本)
int numDistinct(char* s, char* t) {int slen = strlen(s);int tlen = strlen(t);//dp数组含义:以i-1结尾的s中 有 以j-1结尾的t 的个数为dp[i][j]uint64_t** dp = (uint64_t**)malloc(sizeof(uint64_t*) * (slen+1));for(int i = 0; i <= slen;i++){dp[i] = (uint64_t*)malloc(sizeof(uint64_t)* (tlen+1));}//dp初始化:第一列初始化为1,第一行初始化为0for(int j = 1;j <= tlen;j++){dp[0][j] = 0;}for(int i = 0;i <= slen;i++){dp[i][0] = 1;}for(int i = 1;i <= slen;i++){for(int j = 1;j <= tlen;j++){if(s[i-1]==t[j-1]){dp[i][j] = dp[i-1][j-1] + dp[i-1][j];}else {dp[i][j] = dp[i-1][j];}}}uint64_t result = dp[slen][tlen];//打印dp数组for(int i = 0;i <= slen;i++){for(int j = 0;j <= tlen;j++){printf("%d ",dp[i][j]);}}for(int i = 0;i < slen;i++){free(dp[i]);}free(dp);return result;}4.代码实现(C++版本)
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));for (int i = 0; i < s.size(); i++) dp[i][0] = 1;for (int j = 1; j < t.size(); j++) dp[0][j] = 0;for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}}return dp[s.size()][t.size()];}
};三、583. 两个字符串的删除操作
1.题目描述
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
示例 1:
输入: word1 = "sea", word2 = "eat" 输出: 2 解释: 第一步将 "sea" 变为 "ea" ,第二步将 "eat "变为 "ea"
示例 2:
输入:word1 = "leetcode", word2 = "etco" 输出:4
提示:
1 <= word1.length, word2.length <= 500word1和word2只包含小写英文字母
2.解题思路
- 动态规划思路
- 最长公共子序列思路:求出最长公共子序列长度,然后计算这两个字符串长度之和,减去2倍的最长公共子序列,就是我们要求的答案。
3.代码实现(C语言版本)
//min函数
int min(int a,int b){return a>b?b:a;
}int minDistance(char* word1, char* word2) {int len1 = strlen(word1);int len2 = strlen(word2);//dp数组含义:以下标i-1结尾的word1,j-1结尾的word2,使它们相等最小步数为dp[i][j]//初始化二维数组dp,第一行和第一列需要单独初始化,分别表是word1为空,word2以下标j结尾此时移动多少步相等,显然是j步int** dp = (int**)malloc(sizeof(int*)*(len1+1));for(int i = 0;i <= len1;i++){dp[i] = (int*)malloc(sizeof(int) * (len2+1));for(int j = 0;j <= len2;j++){dp[i][j] = 0;}}for(int i = 0;i <= len1;i++){dp[i][0] = i;}for(int j = 0; j <= len2;j++){dp[0][j] = j;}//开始遍历for(int i = 1;i <= len1;i++){for(int j = 1;j <= len2;j++){if(word1[i-1] == word2[j-1]){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] = min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));}}}int result = dp[len1][len2];//freefor(int i = 0;i <= len1;i++){free(dp[i]);}free(dp);return result;
}相关文章:

LeetCode|动态规划|392. 判断子序列、115. 不同的子序列、 583. 两个字符串的删除操作
目录 一、392. 判断子序列 1.题目描述 2.解题思路 3.代码实现(双指针解法) 4.代码实现(动态规划解法) 二、115. 不同的子序列 1.题目描述 2.解题思路 3.代码实现(C语言版本) 4.代码实现(C版本) …...

vscode 阅读 android以及kernel 源码
在Ubuntu系统中安装vscode 参考文档: https://blog.csdn.net/m0_57368670/article/details/127184424 1, 下载vscode https://code.visualstudio.com 2, 安装vscode $ sudo dpkg -i code_1.78.1-1683194560_amd64.deb 3, 打开vscode $ code vscode 阅读 android…...

Intel oneAPI笔记(3)--jupyter官方文档(SYCL Program Structure)学习笔记
前言 本文是对jupyterlab中oneAPI_Essentials/02_SYCL_Program_Structure文档的学习记录,包含对Device Selector、Data Parallel Kernel、Host Accessor、Buffer Destruction、的介绍,最后还有一个小关于向量(Vector)加法的实例 …...

verilog——移位寄存器
在Verilog中,你可以使用移位寄存器来实现数据的移位操作。移位寄存器是一种常用的数字电路,用于将数据向左或向右移动一个或多个位置。这在数字信号处理、通信系统和其他应用中非常有用。以下是一个使用Verilog实现的简单移位寄存器的示例: m…...

C++11 多线程学习笔记
1. thread — 线程篇 所需头文件:<thread> 1.1 构造函数 // 1 默认构造函数 thread() noexcept; // 2 移动构造函数,把other的所有权转移给新的thread对象,之后 other 不再表示执行线程。 thread( thread&& other ) noex…...
nn.embedding函数详解(pytorch)
提示:文章附有源码!!! 文章目录 前言一、nn.embedding函数解释二、nn.embedding函数使用方法四、模型训练与预测的权重变化探讨 前言 最近发现prompt工程(如sam模型),也有transform的detr模型等都使用了nn.Embedding函…...

gitee.com[0: xxx.xx.xxx.xx]: errno=Unknown error
git在提交或拉取代码的时候,遇到以下报错信息: Unable to connect to gitee.com[0: xxx.xx.xxx.xx]: errnoUnknown error 解决问题步骤: 1、找到自己的电脑上的git用户配置文件 文件位置位于:C:\Users\用户名\.gitconfig 比如我…...

bug: https://aip.baidubce.com/oauth/2.0/token报错blocked by CORS policy
还是跟以前一样,我们先看报错点:(注意小编这里是H5解决跨域的,不过解决跨域的原理都差不多) Access to XMLHttpRequest at https://aip.baidubce.com/oauth/2.0/token from origin http://localhost:8000 has been blo…...
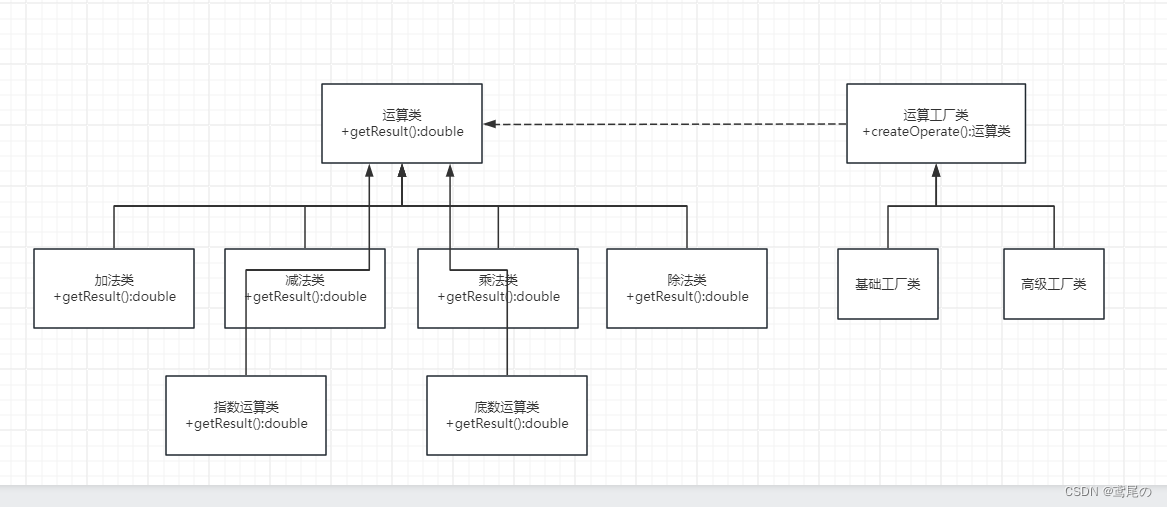
简单工厂VS工厂方法
工厂方法模式–制造细节无需知 前面介绍过简单工厂模式,简单工厂模式只是最基本的创建实例相关的设计模式。在真实情况下,有更多复杂的情况需要处理。简单工厂生成实例的类,知道了太多的细节,这就导致这个类很容易出现难维护、灵…...

使用VSCODE链接Anaconda
打代码还是在VSCODE里得劲 所以得想个办法在VSCODE里运行py文件 一开始在插件商店寻找插件 但是没有发现什么有效果的 幸运的是VSCODE支持自己选择Python的编译器 打开VSCODE 按住CtrlShiftP 输入Select Interpreter 如果电脑已经安装上了Python的环境 VSCODE会默认选择普通…...
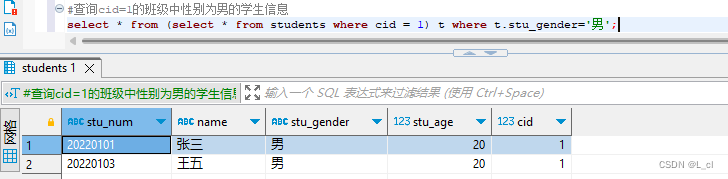
Mysql数据库 9.SQL语言 查询语句 连接查询、子查询
连接查询 通过查询多张表,用连接查询进行多表联合查询 关键字:inner join 内连接 left join 左连接 right join 右连接 数据准备 创建新的数据库:create database 数据库名; create database db_test2; 使用数据库:use 数据…...
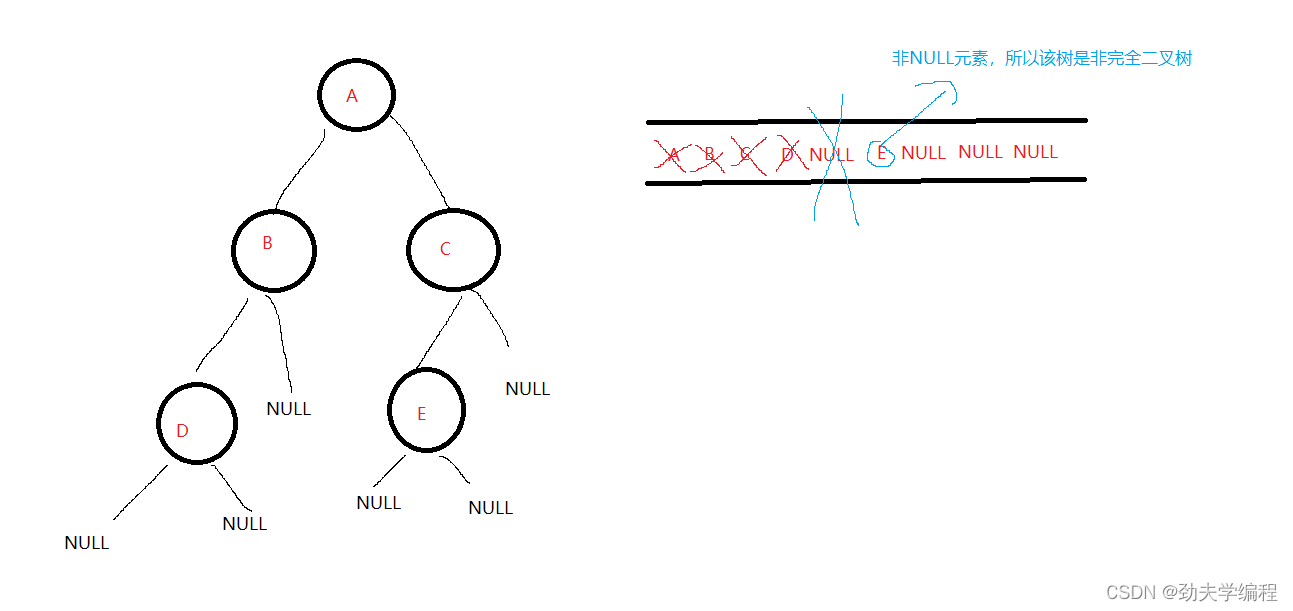
二叉树按二叉链表形式存储,试编写一个判别给定二叉树是否是完全二叉树的算法
完全二叉树:就是每层横着划过去是连起来的,中间不会断开 比如下面的左图就是完全二叉树 再比如下面的右图就是非完全二叉树 那我们可以采用层序遍历的方法,借助一个辅助队列 当辅助队列不空的时候,出队头元素,入队头…...
Android自定义控件
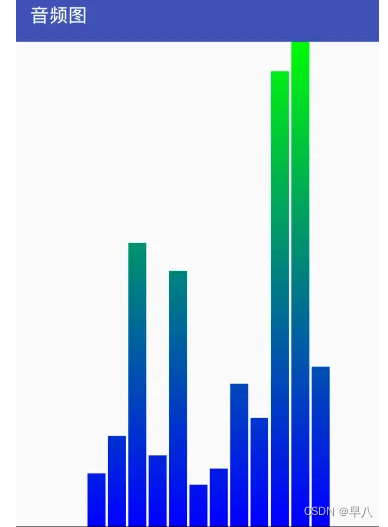
目录 Android自定义控件一、对现有控件进行扩展二、创建复合控件1 定义属性2 组合控件3 引用UI模板 三、重写View来实现全新控件1 弧线展示图1.1 具体步骤: 2 音频条形图2.1 具体步骤 四、补充:自定义ViewGroup Android自定义控件 ref: Android自定义控件…...

Java 中的 Cloneable 接口和深拷贝
引言: 在 Java 中,深拷贝是一种常见的需求,它可以创建一个对象的完全独立副本。Cloneable 接口提供了一种标记机制,用于指示一个类实例可以被复制。本文将详细介绍 Java 中的 Cloneable 接口和深拷贝的相关知识࿰…...
项目实战:通过axios加载水果库存系统的首页数据
1、创建静态页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><link rel"stylesheet" href"style/index.css"><script src"script/axios.mi…...
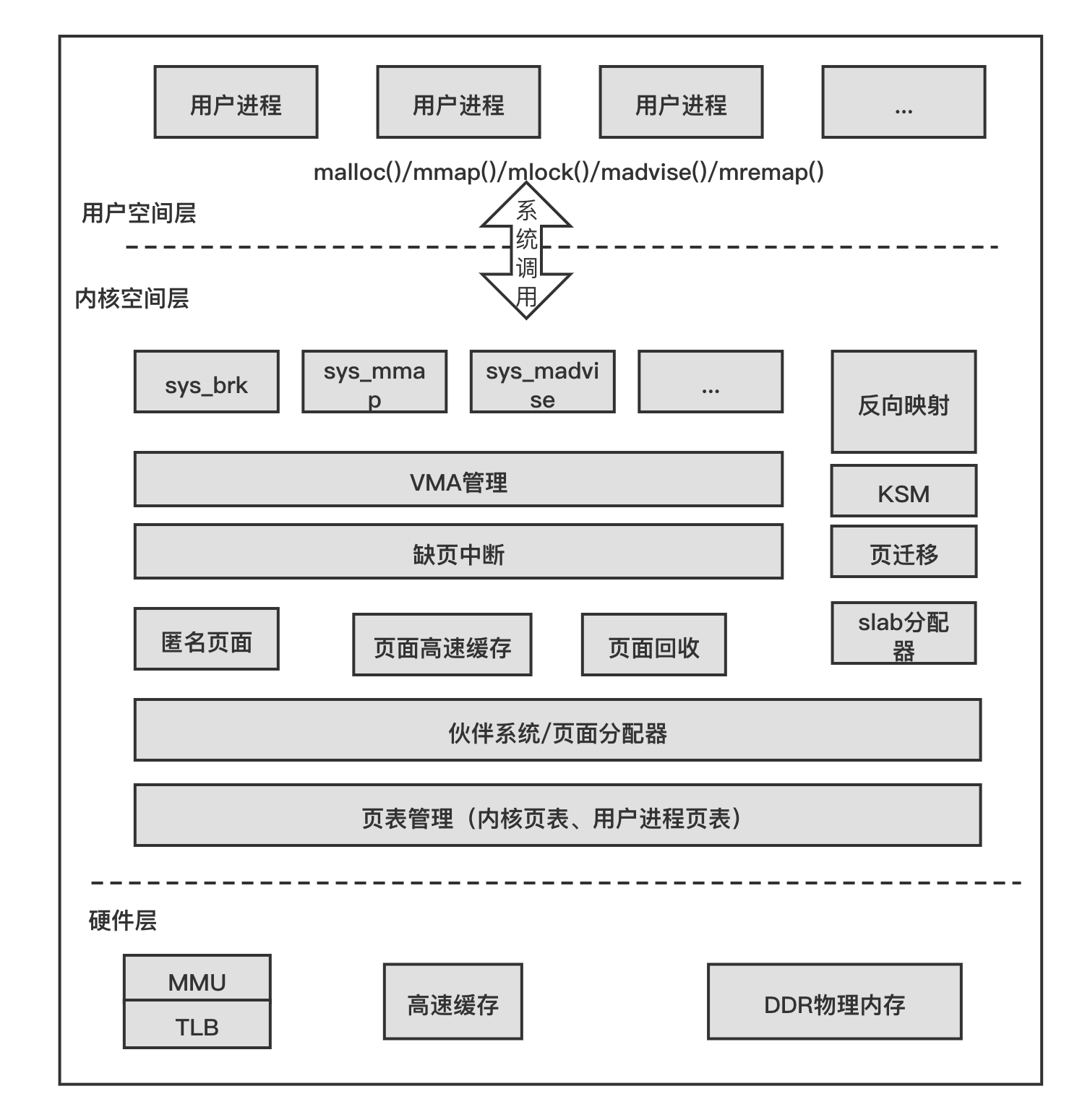
RK3568平台 内存的基本概念
一.Linux的Page Cache page cache,又称pcache,其中文名称为页高速缓冲存储器,简称页高缓。page cache的大小为一页,通常为4K。在linux读写文件时,它用于缓存文件的逻辑内容,从而加快对磁盘上映像和数据的访…...
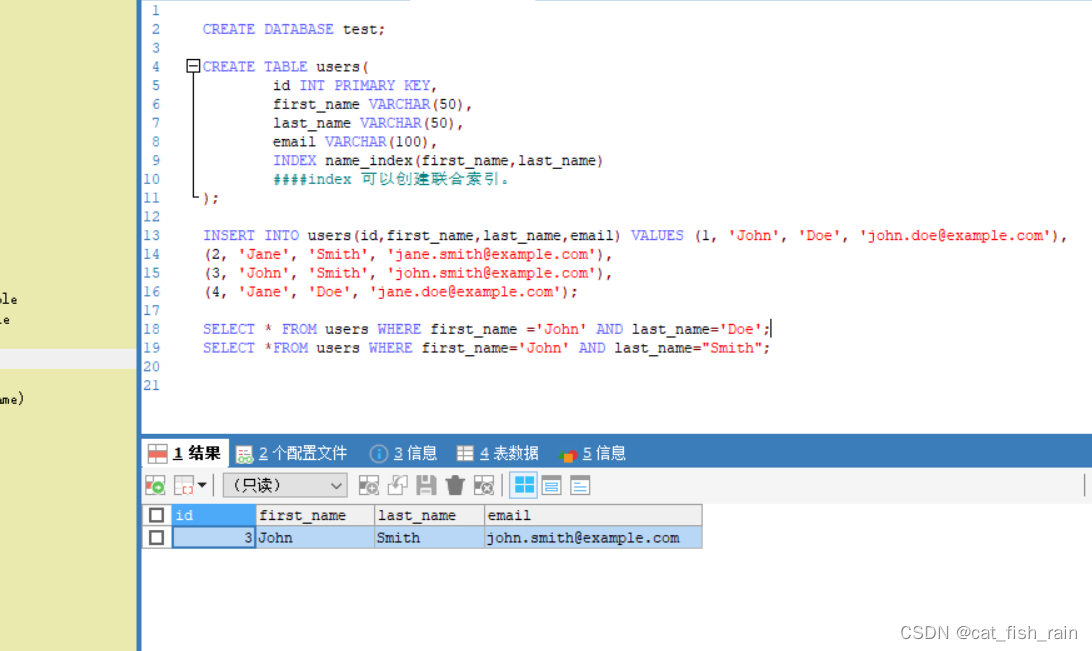
mysql联合索引和最左匹配问题。
1引言: 如果频繁地使⽤相同的⼏个字段查询,就可以考虑建⽴这⼏个字段的联合索引来提⾼查询效率。⽐如对 于联合索引 test_col1_col2_col3,实际建⽴了 (col1)、(col1, col2)、(col, col2, col3) 三个索引。联合 索引的主要优势是减少结果集数量…...

全球发布|首个AI视角下的生态系统架构解读—《生态系统架构--人工智能时代从业者的新思维》重磅亮相!
点击可免费注册下载 👇 人工智能时代的企业架构师必读系列 《生态系统架构--人工智能时代从业者的新思维》 Philip Tetlow、Neal Fishman、Paul Homan、Rahul著 The Open Group Press 2023年11月出版 这本书可以很好地帮助全球架构师使用人工智能来构建、开发和…...

解决torch.hub.load加载网络模型异常
1 torch.hub.load 加载网络模型错误 通过网络使用torch.hub.load加载模型代码如下: self.model torch.hub.load("facebookresearch/dinov2", dinov2_vits14, sourcegithub).to(self.device) 运行网上的项目,经常会卡住或者超时,…...
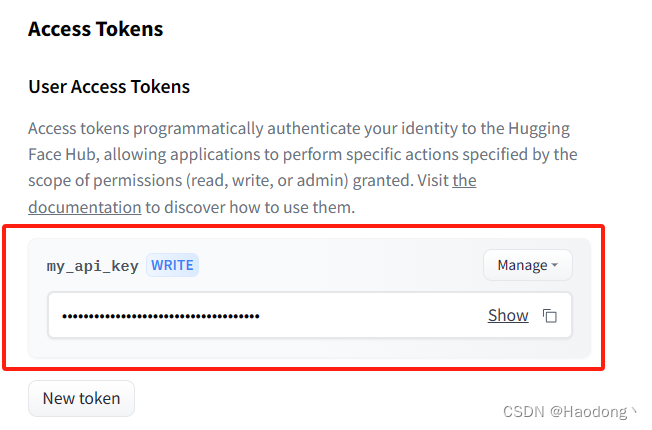
如何获取HuggingFace的Access Token;如何获取HuggingFace的API Key
Access Token通过编程方式向 HuggingFace 验证您的身份,允许应用程序执行由授予的权限范围(读取、写入或管理)指定的特定操作。您可以通过以下步骤获取: 1.首先,你需要注册一个 Hugging Face 账号。如果你已经有了账号…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
