二叉树按二叉链表形式存储,试编写一个判别给定二叉树是否是完全二叉树的算法
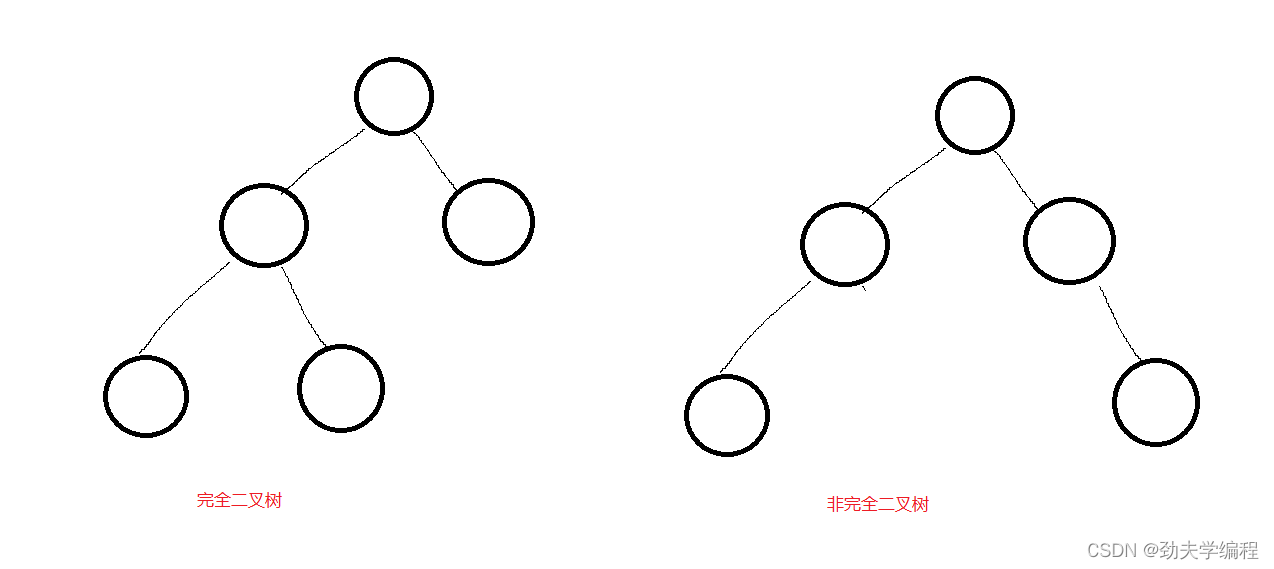
完全二叉树:就是每层横着划过去是连起来的,中间不会断开
比如下面的左图就是完全二叉树
再比如下面的右图就是非完全二叉树
那我们可以采用层序遍历的方法,借助一个辅助队列
当辅助队列不空的时候,出队头元素,入队头元素的左右孩子
这里不同于层序遍历的是,我们这里入左右孩子,如果左右孩子是NULL,我们也入队
当我们在重复执行上面的操作时,我们会有一刻出队列的时候遇到NULL的情况
这时,再对队列的剩余元素进行判断,如果全是NULL则是完全二叉树,否则是非完全二叉树
举例如下
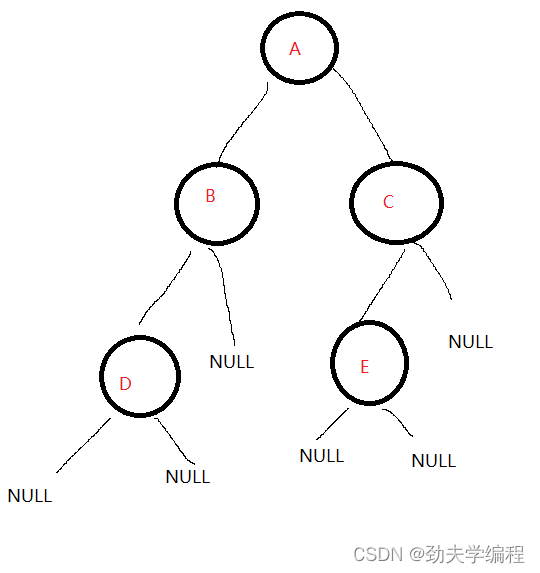
先把根节点A入队
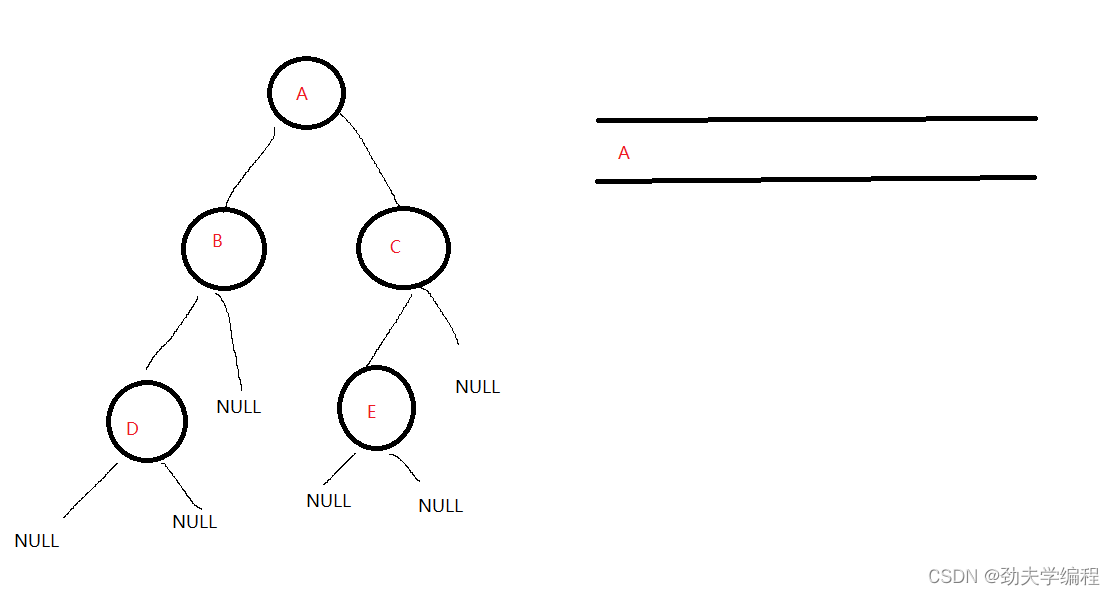
然后队列不空,队头A出队,A的左右孩子BC入队
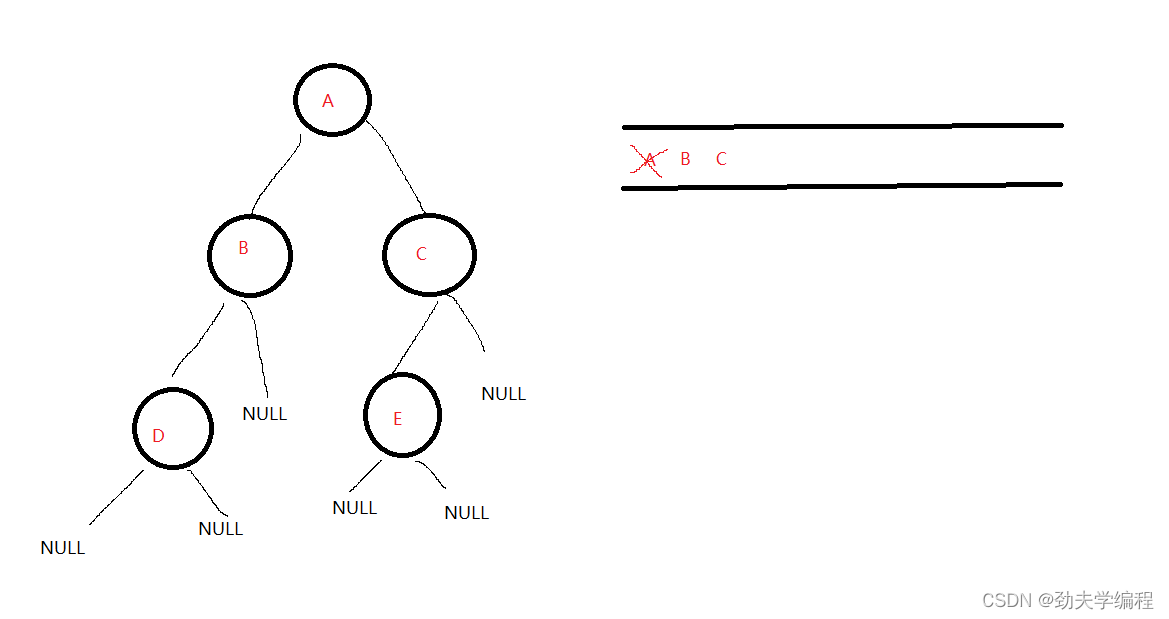
然后队列不空,队头B出队,B的左孩子D 和NULL入队
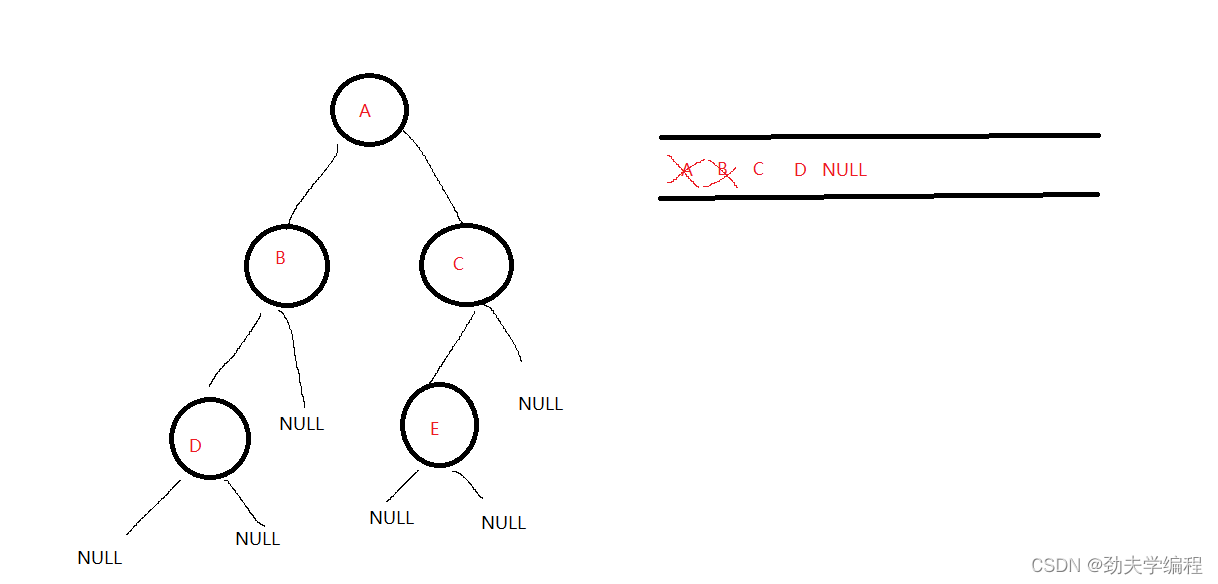
然后队列不空,队头C出队,C的左右孩子E 和NULL入队
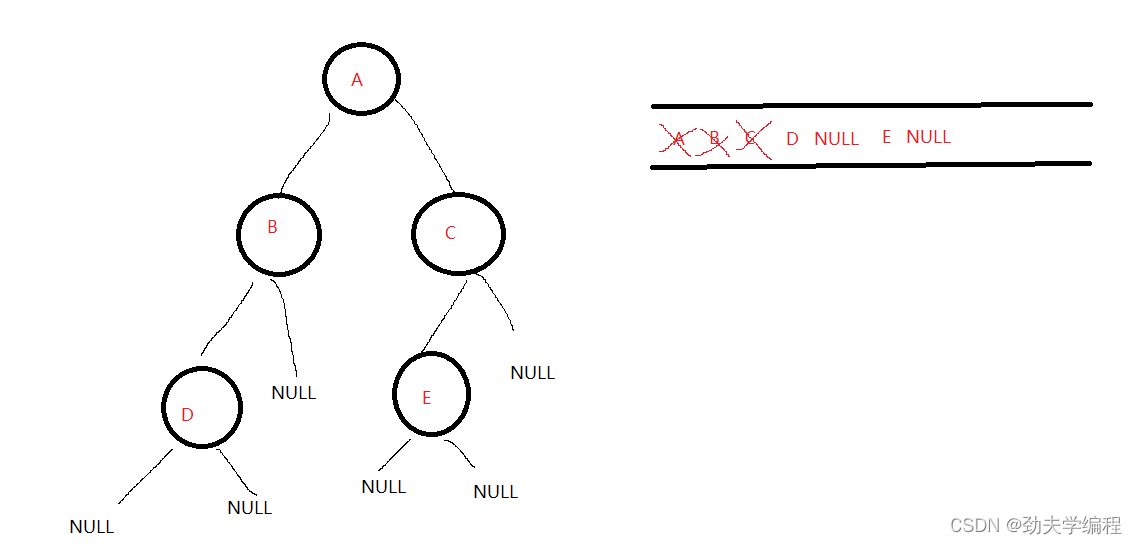
然后队列不空,队头D出队,D的左右孩子NULL入队
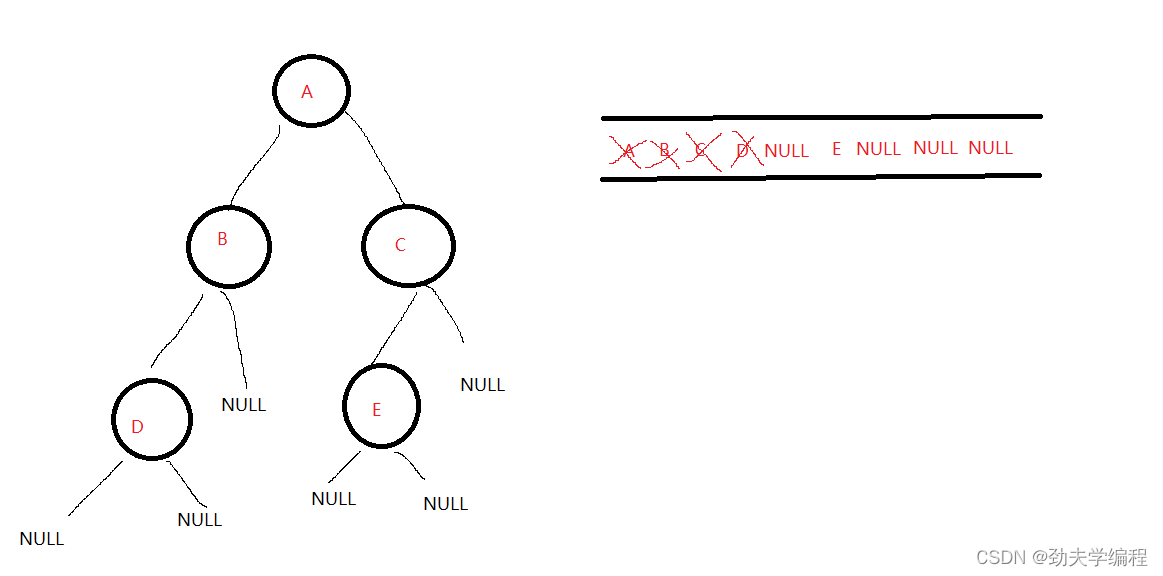
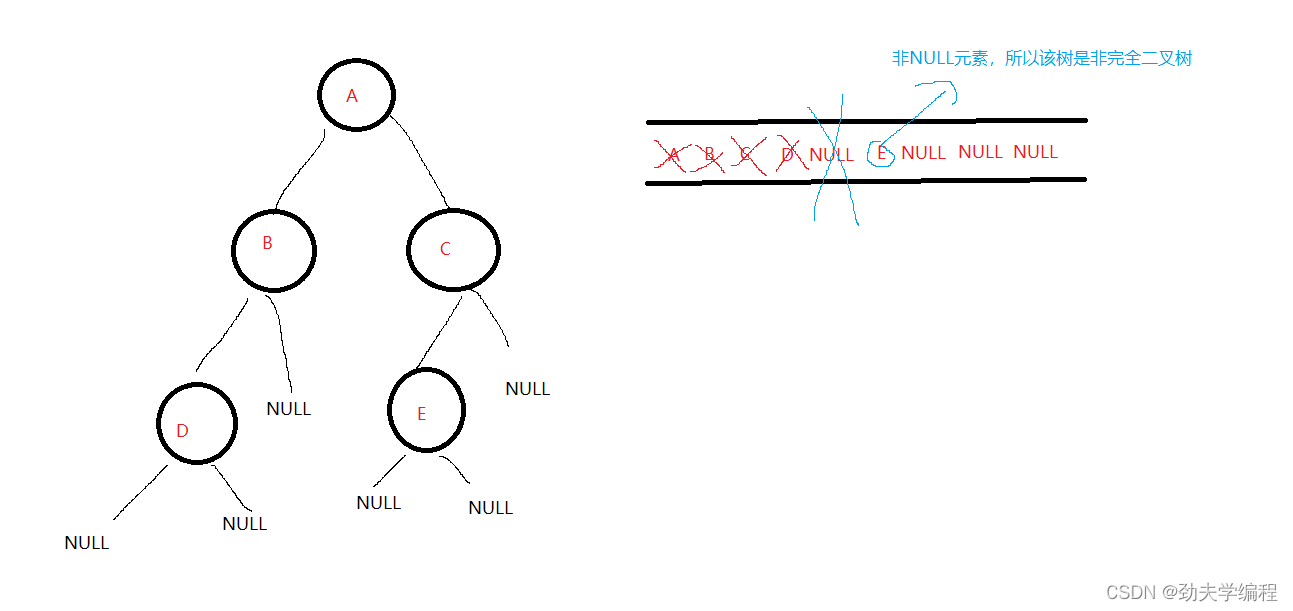
接下来,队不空,出队的元素是NULL
对于这种情况,我们就需要把队列剩余元素看一下了,如果队列剩余元素中有非NULL元素,
那么该树就不是完全二叉树
代码如下:
//队列相关操作
void InitQueue(SqQueue* Q);//初始化队列
void EnQueue(SqQueue* Q,BiTree T);//入队
void DeQueue(SqQueue* Q,BiTree* T)//出队头元素,用T带回出队元素
int QueueEmpty(SqQueue Q);//判断队列是否为空//判断是否是完全二叉树
int IsComplete(BiTree T){if(T==NULL){//空树是一种特殊的完全二叉树return 1;}SqQueue Q;//初始化一个辅助队列InitQueue(&Q);EnQueue(&Q,T);//根节点入队while(!QueueEmpty(Q)){//层序遍历BiTree p;DeQueue(&Q,&p);if(p!=NULL){//出的队头元素非空//左右孩子入队EnQueue(&Q,p->lchild);EnQueue(&Q,p->rchild);}else{//出的队头元素是NULL//判断队列中剩余元素是否全是NULL//全是NULL——完全二叉树//不全是NULL——非完全二叉树while(!QueueEmpty(Q)){DeQueue(&Q,&p);if(p!=NULL){return 0;}}}}return 1;
}
相关文章:

二叉树按二叉链表形式存储,试编写一个判别给定二叉树是否是完全二叉树的算法
完全二叉树:就是每层横着划过去是连起来的,中间不会断开 比如下面的左图就是完全二叉树 再比如下面的右图就是非完全二叉树 那我们可以采用层序遍历的方法,借助一个辅助队列 当辅助队列不空的时候,出队头元素,入队头…...
Android自定义控件
目录 Android自定义控件一、对现有控件进行扩展二、创建复合控件1 定义属性2 组合控件3 引用UI模板 三、重写View来实现全新控件1 弧线展示图1.1 具体步骤: 2 音频条形图2.1 具体步骤 四、补充:自定义ViewGroup Android自定义控件 ref: Android自定义控件…...

Java 中的 Cloneable 接口和深拷贝
引言: 在 Java 中,深拷贝是一种常见的需求,它可以创建一个对象的完全独立副本。Cloneable 接口提供了一种标记机制,用于指示一个类实例可以被复制。本文将详细介绍 Java 中的 Cloneable 接口和深拷贝的相关知识࿰…...
项目实战:通过axios加载水果库存系统的首页数据
1、创建静态页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title><link rel"stylesheet" href"style/index.css"><script src"script/axios.mi…...
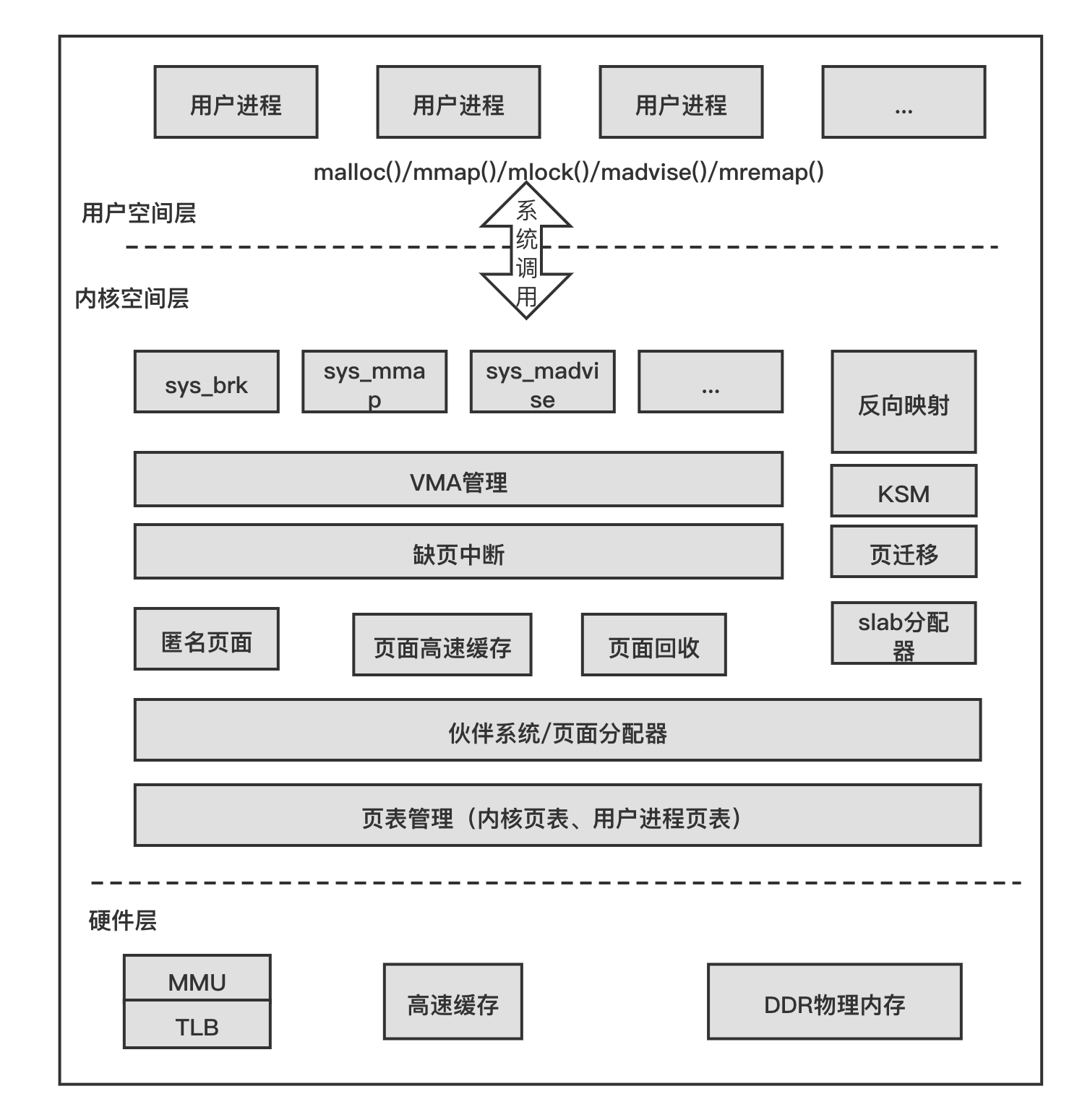
RK3568平台 内存的基本概念
一.Linux的Page Cache page cache,又称pcache,其中文名称为页高速缓冲存储器,简称页高缓。page cache的大小为一页,通常为4K。在linux读写文件时,它用于缓存文件的逻辑内容,从而加快对磁盘上映像和数据的访…...
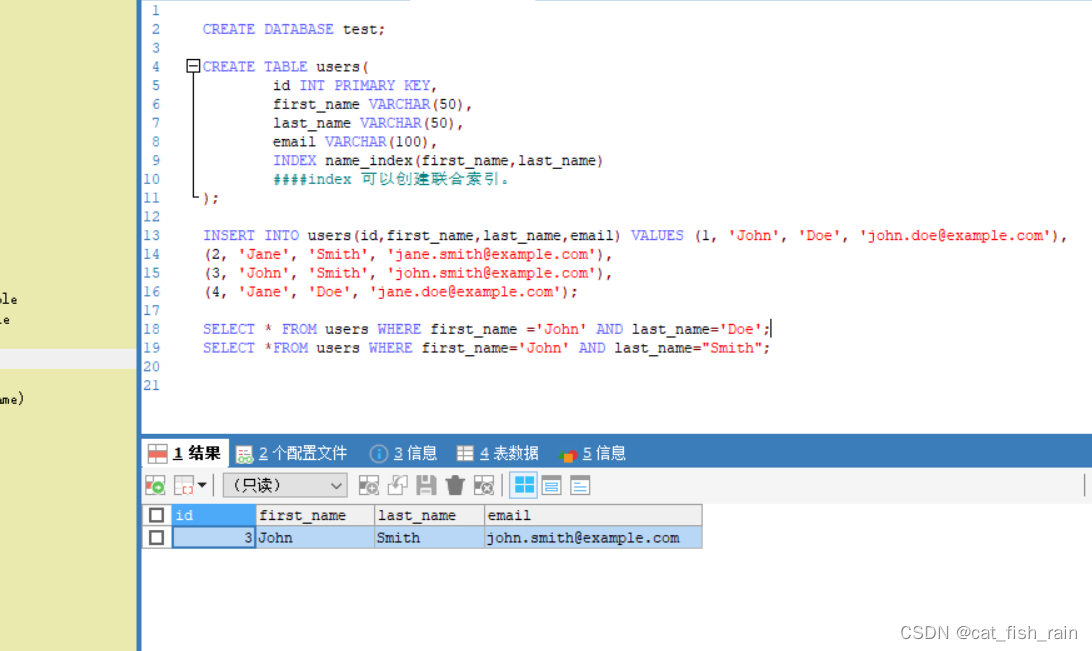
mysql联合索引和最左匹配问题。
1引言: 如果频繁地使⽤相同的⼏个字段查询,就可以考虑建⽴这⼏个字段的联合索引来提⾼查询效率。⽐如对 于联合索引 test_col1_col2_col3,实际建⽴了 (col1)、(col1, col2)、(col, col2, col3) 三个索引。联合 索引的主要优势是减少结果集数量…...

全球发布|首个AI视角下的生态系统架构解读—《生态系统架构--人工智能时代从业者的新思维》重磅亮相!
点击可免费注册下载 👇 人工智能时代的企业架构师必读系列 《生态系统架构--人工智能时代从业者的新思维》 Philip Tetlow、Neal Fishman、Paul Homan、Rahul著 The Open Group Press 2023年11月出版 这本书可以很好地帮助全球架构师使用人工智能来构建、开发和…...

解决torch.hub.load加载网络模型异常
1 torch.hub.load 加载网络模型错误 通过网络使用torch.hub.load加载模型代码如下: self.model torch.hub.load("facebookresearch/dinov2", dinov2_vits14, sourcegithub).to(self.device) 运行网上的项目,经常会卡住或者超时,…...
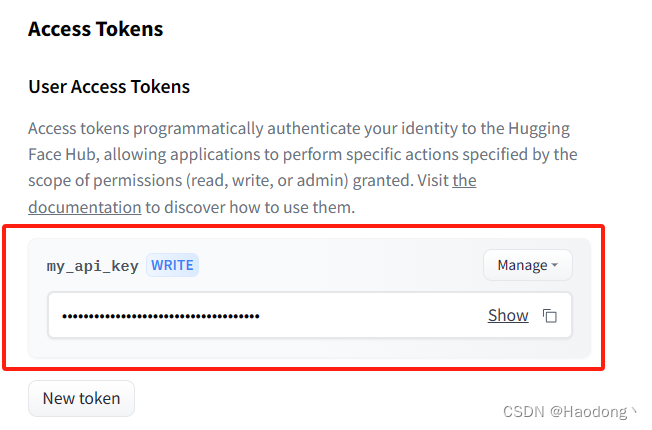
如何获取HuggingFace的Access Token;如何获取HuggingFace的API Key
Access Token通过编程方式向 HuggingFace 验证您的身份,允许应用程序执行由授予的权限范围(读取、写入或管理)指定的特定操作。您可以通过以下步骤获取: 1.首先,你需要注册一个 Hugging Face 账号。如果你已经有了账号…...

How to resolve jre-openjdk and jre-openjdk-headless conflicts?
2023-11-05 Archlinux 执行 pacman -Syu 显示 failed to prepare transaction;jre-openjdk and jre-openjdk-headless conflicts 解决 archlinux sudo pacman -Sy jdk-openjdk...

setTimeout和setImmediate以及process.nextTick的区别?
目录 前言 setTimeout 特性和用法 setImmediate 特性和用法 process.nextTick 特性和用法 区别和示例 总结 在Node.js中,setTimeout、setImmediate和process.nextTick是用于调度异步操作的三种不同机制。它们之间的区别在于事件循环中的执行顺序和优先级。…...

read 方法为什么返回 int 类型
在Java的输入流(InputStream)中,read方法返回int类型的值的原因是为了提供更多的信息和灵活性。虽然这可能看起来有些不直观,但有一些合理的考虑和用途,主要包括以下几点: EOF标志:read方法返回…...

在二维矩阵/数组中查找元素 Leetcode74, Leetcode240
这一类题型中二维数组的元素取值有序变化,因此可以用二分查找法。我们一起来看一下。 一、Leetcode 74 Leetcode 74. 搜索二维矩阵 这道题要在一个二维矩阵中查找元素。该二维矩阵有如下特点: 每行元素 从左到右 按非递减顺序排列。每行的第一个元素 …...
MS35657步进电机驱动器可兼容DRV8824
MS35657 是一款双通道 DMOS 全桥驱动器,可以驱动一个步进电机或者两个直流电机。可兼容DRV8824(功能基本一致,管脚不兼容)。每个全桥的驱动电流在 24V 电源下可以工作到 1.4A。MS35657 集成了固定关断时间的 PWM 电流校正器&#…...

SQL语句性能优化
1、查询 SQL 尽量不要使用 select *,而是 select 具体字段 反例子: select * from sys_user; 正例子: select id,name from sys_user; 理由如下: 只取需要的字段,节省资源、减少网络开销。select * 进行查询时,很可能就不会使用到覆盖索引了,就会造成回表查询。…...
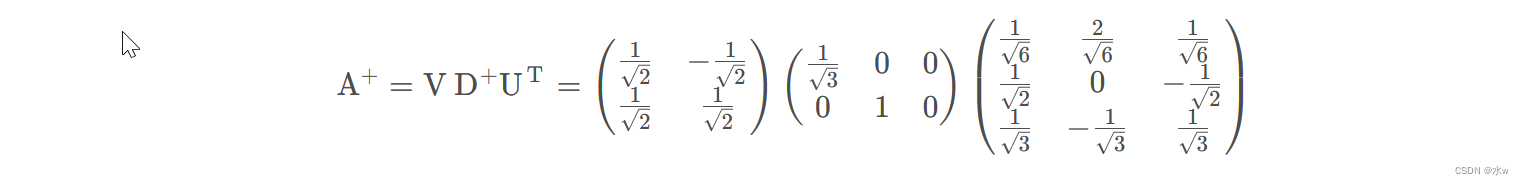
线性代数之 伪逆矩阵
目录 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD ◼ 用Python代码计算A的伪逆矩阵 ◼ 笔算A的伪逆矩阵 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD 逆矩阵并不总是存在,即使是方阵。然而,对于非正方形矩阵,存在一个伪逆矩阵,也叫摩尔-彭罗斯…...

【3D图像分割】基于Pytorch的VNet 3D 图像分割5(改写数据流篇)
在这篇文章:【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割2(基础数据流篇) 的最后,我们提到了: 在采用vent模型进行3d数据的分割训练任务中,输入大小是16*96*96,这个的裁剪是放到Dataset类…...
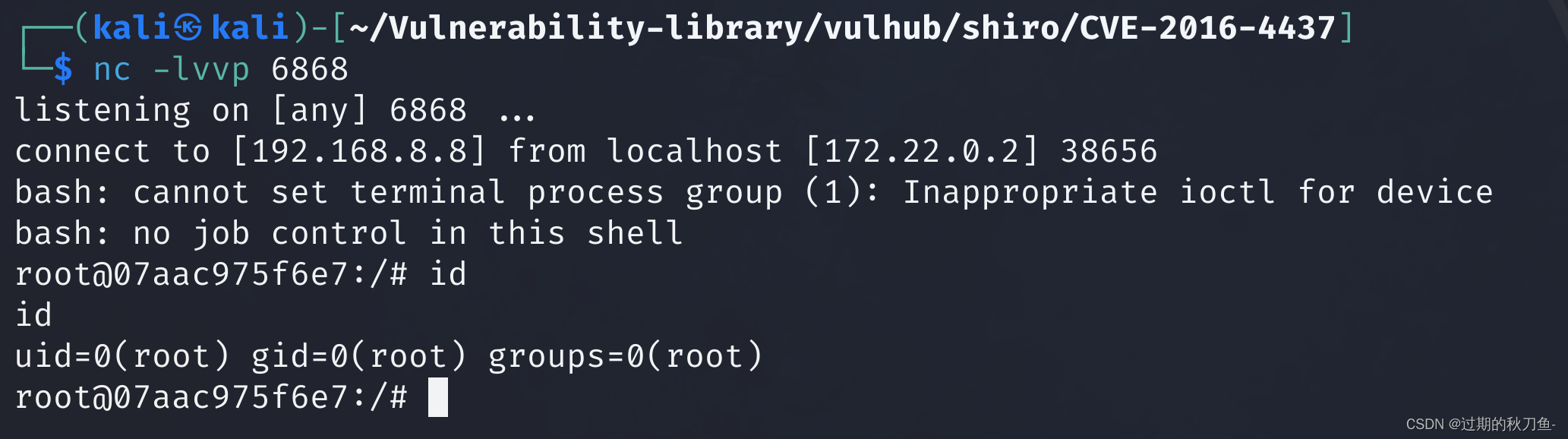
【漏洞复现】Apache_Shiro_1.2.4_反序列化漏洞(CVE-2016-4437)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞分析3、漏洞验证 说明内容漏洞编号CVE-2016-4437漏洞名称Apache_Shiro_1.2.4_反序列化漏洞漏洞评级…...

Mac连接linux的办法(自带终端和iterm2)
1. 使用Mac自带终端Terminal 1.1 点击右上角的聚焦搜索,再输入终端 1.2 查找linux系统的ip地址 在虚拟机里输入如下命令,找到蓝色区域的就是ip地址 ip addr 如果没有显示ip地址,可以重新安装一下虚拟机,之后确保以太网的连接是打…...
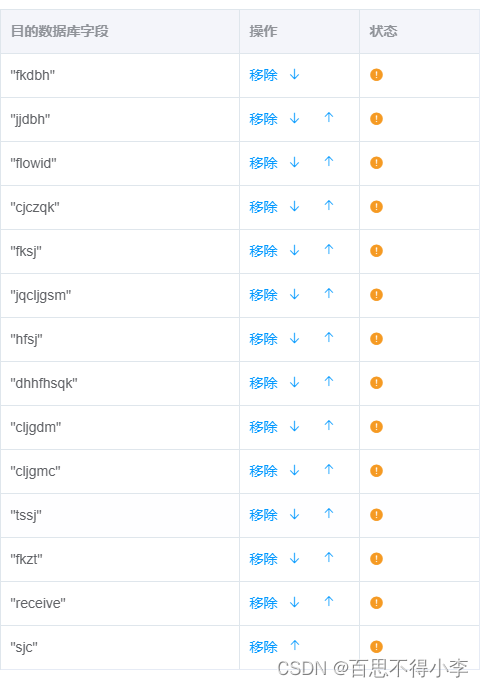
js调整table表格上下相邻元素顺序
有时候我们会遇到要通过箭头控制table表格上下顺序的需求,如下: 点击向下就将该元素下移一位,下面的一位元素就移上来,点击向上就将该元素上移一位,上面的一位元素就移下来,也就是相邻元素互换位置顺序: <el-table :data="targetTable" border style=&quo…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
