在二维矩阵/数组中查找元素 Leetcode74, Leetcode240
这一类题型中二维数组的元素取值有序变化,因此可以用二分查找法。我们一起来看一下。
一、Leetcode 74
Leetcode 74. 搜索二维矩阵 这道题要在一个二维矩阵中查找元素。该二维矩阵有如下特点:
- 每行元素 从左到右 按非递减顺序排列。
- 每行的第一个元素 > 前一行的最后一个元素。
也就是说,这种二维数组的元素逐行、逐列递增变化,如下图所示,沿箭头方向元素值递增:

方法一:做两次二分查找。
- 先在第一列中查找值为 target 的元素所在行。
- 再在这一行中查找值为 target 的元素所在列。
在这两步中,难点在于第一步确定 target 所在行。以图中的示例矩阵为例,要寻找 3,如何定位到 3 所在行呢?在第一列的元素中,3 所在行的第一列元素 1 是小于 3 的元素中最接近 3 的元素,这就是第一步的思路:在第一列元素中查找小于等于 target、且最接近 target 的元素。这里可以用 Leetcode 69 所使用的方法(欢迎阅读文章:二分查找法搜寻元素 Leetcode35, Leetcode69,其中详细介绍了这类问题的两种解决方法,本文采用了其中一种方法。)
相应的 Python 代码和注释为:
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:# 第一步:查找元素所在行low, high = 0, len(matrix) - 1while low <= high:mid = low + (high - low) // 2# 注意:这里是在第 1 列查找,# mid元素索引为 matrix[mid][0]。if matrix[mid][0] == target:return Trueelif matrix[mid][0] > target:high = mid - 1else:low = mid + 1# 确定元素所在行(row)row = high# 第二步:查找元素所在列low, high = 0, len(matrix[0]) - 1while low <= high:mid = low + (high - low) // 2# 注意:这里是在第 row 行查找,# mid元素索引为 matrix[row][mid]。if matrix[row][mid] == target:return Trueelif matrix[row][mid] > target:high = mid - 1else:low = mid + 1return False
方法二:把二维矩阵看作一个一维数组处理。
因为矩阵的元素是按升序排列,我们在处理时可以把它想象成连续的一维序列,就像上图示例矩阵中的元素,在脑子里把它“拼接”成一个连续的一维数组,[1,3,5,7,10,11,16,20,23,30,34,60],在这个升序数组里查找元素很容易。
但是,这个一维数组索引只是我们为了解决问题做的设想,实际中矩阵元素是以二维数组形式存储的,因此每次索引元素值时还需要一个操作:把(设想的)一维数组索引换算回(实际的)二维数组索引。
相应的 Python 代码和注释为:
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:# 求 mxn 矩阵的维度大小m = len(matrix)n = len(matrix[0])# 按“一维”有序数组处理length = m*nlow, high = 0, length - 1while low <= high:mid = low + (high - low) // 2# 关键:索引时要把(设想的)一维数组索引换算回(实际的)二维数组索引。mid_row = mid // nmid_col = mid % nmid_val = matrix[mid_row][mid_col] if mid_val == target:return Trueelif mid_val > target:high = mid - 1else:low = mid + 1return False
方法二实现起来比方法一更简洁,但是我在 Leetcode 运行代码时发现方法二比方法一的耗时大。
二、Leetcode 240
Leetcode 240. 搜索二维矩阵 II 这道题也是在二维矩阵中查找元素。不同的是,这里的二维矩阵有如下特点:
- 每行的元素 从左到右 升序排列。
- 每列的元素 从上到下 升序排列。
下图所示为一个示例矩阵:

这道题的巧妙之处在于中点 mid 的选择。
根据给定矩阵的升序排列特点,一个元素位于第 i 行、第 j 列,则该元素所在行第 0 ~ ( j - 1 ) 列的元素都比它小;该元素所在列第 ( i + 1 ) ~ ( m - 1 ) 行的元素都比它大。具体来说,以上图的示例矩阵为例,如绿色箭头标识所示,以圆圈中的元素 8 为中点,[ 2, 5, 8, 9, 14, 23 ] 这些元素就构成了一个升序排列的数组。也就是说,以第 i 行、第 j 列的元素为直角,其所在行和列元素构成的 倒 “L” 形状序列 是一个有序数组,而在直角的这个元素就是数组的中点。在这个数组中可以用二分查找:比较中点的元素与目标值 target 的大小决定下一步的寻找范围。如果该元素大于 target,就往左移一列:j - 1。如果该元素小于 target,就往下移一行:i + 1。
应该从哪里开始呢?选择右上角的元素(第 0 行,(n-1) 列)做为起始 mid 元素,逐步推进到左下角元素。时间复杂度是 O(m+n)。这一点您可以试一下,如果要找的元素位于左下角,正好要走 m+ n 步。
相应的 Python 代码为:
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:m, n = len(matrix), len(matrix[0])i, j = 0, n - 1while i < m and j >= 0:if matrix[i][j] == target:return Trueelif matrix[i][j] > target:j -= 1else:i += 1return False
本文对您有帮助的话,请点赞支持一下吧,谢谢!
关注我 宁萌Julie,互相学习,多多交流呀!
参考
1.Leetcode 74 方法二思路:Don’t treat it as a 2D matrix, just treat it as a sorted list - Search a 2D Matrix - LeetCode
2.Leetcode 240 思路:My concise O(m+n) Java solution - Search a 2D Matrix II - LeetCode
相关文章:

在二维矩阵/数组中查找元素 Leetcode74, Leetcode240
这一类题型中二维数组的元素取值有序变化,因此可以用二分查找法。我们一起来看一下。 一、Leetcode 74 Leetcode 74. 搜索二维矩阵 这道题要在一个二维矩阵中查找元素。该二维矩阵有如下特点: 每行元素 从左到右 按非递减顺序排列。每行的第一个元素 …...
MS35657步进电机驱动器可兼容DRV8824
MS35657 是一款双通道 DMOS 全桥驱动器,可以驱动一个步进电机或者两个直流电机。可兼容DRV8824(功能基本一致,管脚不兼容)。每个全桥的驱动电流在 24V 电源下可以工作到 1.4A。MS35657 集成了固定关断时间的 PWM 电流校正器&#…...

SQL语句性能优化
1、查询 SQL 尽量不要使用 select *,而是 select 具体字段 反例子: select * from sys_user; 正例子: select id,name from sys_user; 理由如下: 只取需要的字段,节省资源、减少网络开销。select * 进行查询时,很可能就不会使用到覆盖索引了,就会造成回表查询。…...
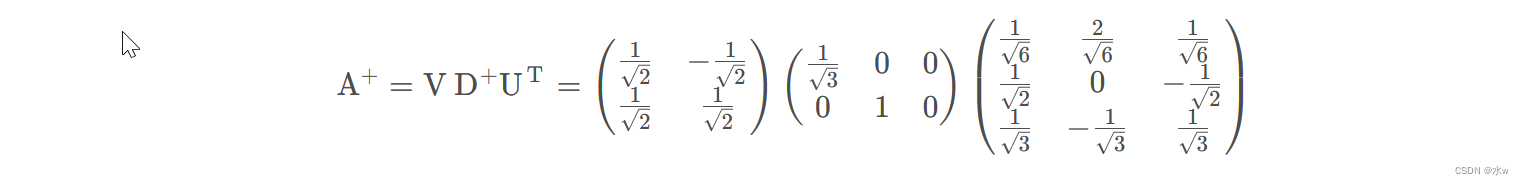
线性代数之 伪逆矩阵
目录 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD ◼ 用Python代码计算A的伪逆矩阵 ◼ 笔算A的伪逆矩阵 一、伪逆矩阵 ◼ A的伪逆矩阵与SVD 逆矩阵并不总是存在,即使是方阵。然而,对于非正方形矩阵,存在一个伪逆矩阵,也叫摩尔-彭罗斯…...

【3D图像分割】基于Pytorch的VNet 3D 图像分割5(改写数据流篇)
在这篇文章:【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割2(基础数据流篇) 的最后,我们提到了: 在采用vent模型进行3d数据的分割训练任务中,输入大小是16*96*96,这个的裁剪是放到Dataset类…...
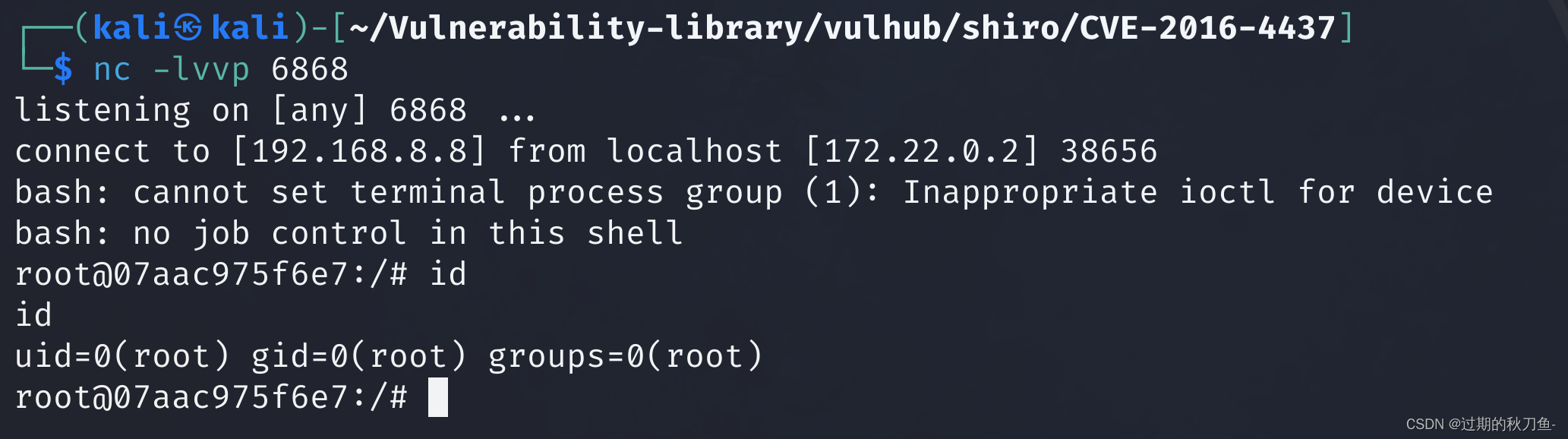
【漏洞复现】Apache_Shiro_1.2.4_反序列化漏洞(CVE-2016-4437)
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞分析3、漏洞验证 说明内容漏洞编号CVE-2016-4437漏洞名称Apache_Shiro_1.2.4_反序列化漏洞漏洞评级…...

Mac连接linux的办法(自带终端和iterm2)
1. 使用Mac自带终端Terminal 1.1 点击右上角的聚焦搜索,再输入终端 1.2 查找linux系统的ip地址 在虚拟机里输入如下命令,找到蓝色区域的就是ip地址 ip addr 如果没有显示ip地址,可以重新安装一下虚拟机,之后确保以太网的连接是打…...
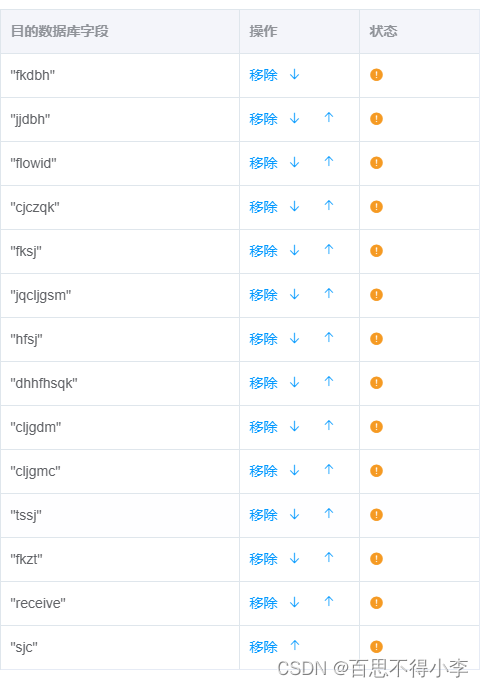
js调整table表格上下相邻元素顺序
有时候我们会遇到要通过箭头控制table表格上下顺序的需求,如下: 点击向下就将该元素下移一位,下面的一位元素就移上来,点击向上就将该元素上移一位,上面的一位元素就移下来,也就是相邻元素互换位置顺序: <el-table :data="targetTable" border style=&quo…...
基于ruoyi框架项目-部署到服务器上
基于ruoyi框架项目-部署到服务器上 文章目录 基于ruoyi框架项目-部署到服务器上1.前端vue编译,后的dist下内容打包(前后端分离版本需要)2.后端打包成jar包(如果是thymeleaf仅需打包jar)3.上传到服务器目录下4. docker部…...
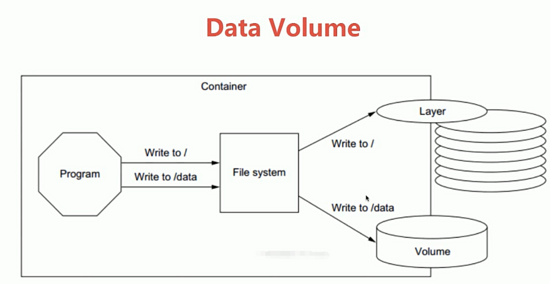
Docker 持久化存储和数据共享_Volume
有些容器会自动产生一些数据,为了不让数据随着 container 的消失而消失,保证数据的安全性。例如:数据库容器,数据表的表会产生一些数据,如果我把 container 给删除,数据就丢失。为了保证数据不丢失…...

万宾科技智能井盖监测仪器助力建设数字化城市
市政公共设施建设在近几年来发展迅速,市政设备的更新换代,资产管理等也成为其中的重要一项。在市政设施建设过程中,井盖也是不可忽视的,一方面,根据传统的管理井盖模式来讲,缺乏有效的远程监控管理方法和手…...
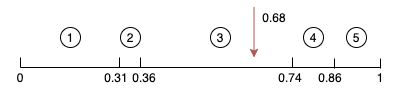
第十一章《搞懂算法:聚类是怎么回事》笔记
聚类是机器学习中一种重要的无监督算法,可以将数据点归结为一系列的特定组合。归为一类的数据点具有相同的特性,而不同类别的数据点则具有各不相同的属性。 11.1 聚类算法介绍 人们将物理或抽象对象的集合分成由类似 的对象组成的多个类的过程被称为聚…...
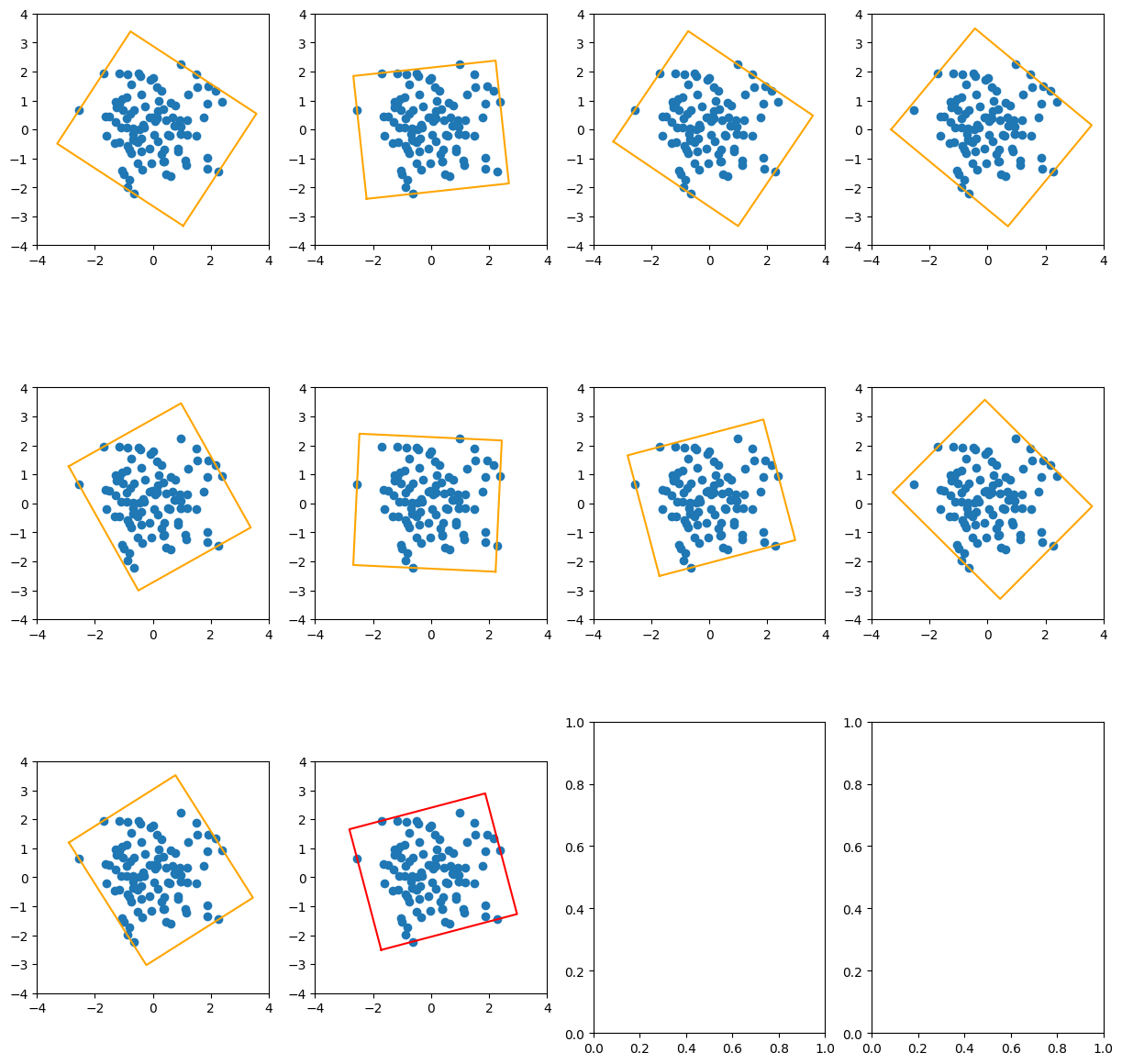
给定n个点或一个凸边形,求其最小外接矩形,可视化
这里写目录标题 原理代码 原理 求n个点的最小外接矩形问题可以等价为先求这n个点的凸包,再求这个凸包的最小外接矩形。 其中求凸包可以使用Graham-Scan算法 需要注意的是, 因为Graham-Scan算法要求我们从先找到凸包上的一个点,所以我们可以先…...

蓝桥杯每日一题2023.11.6
取位数 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 由题意我们知道len中为现阶段长度,如果其与k相等也就是找到了正确的位数,否则就调用递归来进行搜索,每次搜索一位数。 #include <stdio.h> // 求x用10进制表示时的数位长度 int …...
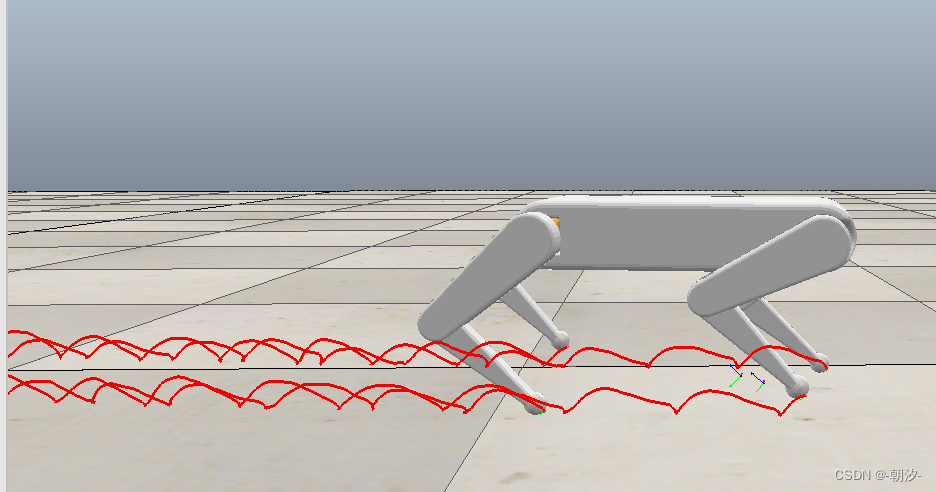
V-REP和Python的联合仿真
机器人仿真软件 各类免费的的机器人仿真软件优缺点汇总_robot 仿真 软件收费么_dyannacon的博客-CSDN博客 课程地址 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_605af87be4b007b4183a42e7 课程资料 guyueclass: 古月学院课程代码 旋转变换 旋转的左乘与…...

WPF布局控件之DockPanel布局
前言:博主文章仅用于学习、研究和交流目的,不足和错误之处在所难免,希望大家能够批评指出,博主核实后马上更改。 概述: DockPanel 位置子控件基于子 Dock 属性,你有 4 个选项停靠,左 (默认) &…...
【实战Flask API项目指南】之二 Flask基础知识
实战Flask API项目指南之 Flask基础知识 本系列文章将带你深入探索实战Flask API项目指南,通过跟随小菜的学习之旅,你将逐步掌握Flask 在实际项目中的应用。让我们一起踏上这个精彩的学习之旅吧! 前言 当小菜踏入Flask后端开发的世界&…...
C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结)
Linux 编译链接那些事儿(02)C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结
1 问题背景说明 在自己的项目源码中引用libeasysqlite.so时编译成功,但运行时遇到问题直接报错,找不到符号 symbol:_ZN3sql5FieldC1ENSt3__112basic_stringIcNS1_11char_traitsIcEENS1_9allocatorIcEEEENS_10field_typeEi。 2 问题描述和解…...
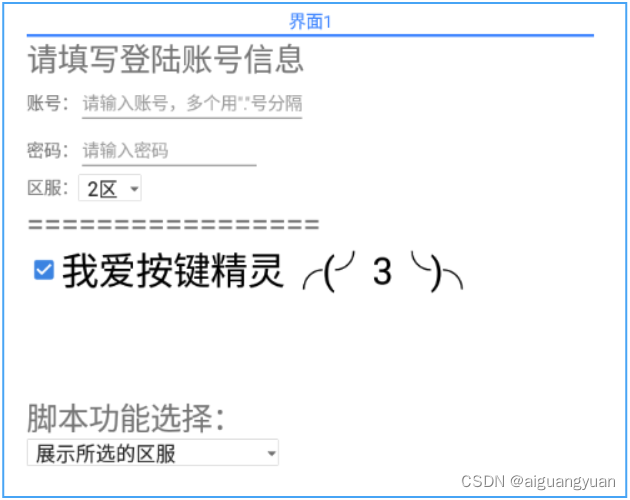
按键精灵中的UI界面操作
1. 按键精灵中UI界面常用的控件 1. 文字框 界面1: {标签页1:{文字框:{名称:"文字框1",显示内容:"显示内容",文字大小:0,高度:0,宽度:0,注释:"文字大小、高度、宽度是可选属性,如需使用默认值,可保持值为0或直接删除此属性&qu…...

dpdk 程序如何配置网卡收发包队列描述符配置?
问题描述 dpdk 程序在配置网卡队列时会涉及收发包队列描述符数量配置问题,收发包描述符的数量看似是一个简单的配置,却对转发性能有着一定的影响。实际业务程序中,收发包描述符大小配置一般参考 dpdk 内部示例程序配置进行,经验之…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
