【C/PTA】循环结构进阶练习(二)
本文结合PTA专项练习带领读者掌握循环结构,刷题为主注释为辅,在代码中理解思路,其它不做过多叙述。
7-1 二分法求多项式单根
二分法求函数根的原理为:如果连续函数f(x)在区间[a,b]的两个端点取值异号,即f(a)f(b)<0,则它在这个区间内至少存在1个根r,即f®=0。
二分法的步骤为:
- 检查区间长度,如果小于给定阈值,则停止,输出区间中点(a+b)/2;否则
- 如果f(a)f(b)<0,则计算中点的值f((a+b)/2);
- 如果f((a+b)/2)正好为0,则(a+b)/2就是要求的根;否则
- 如果f((a+b)/2)与f(a)同号,则说明根在区间[(a+b)/2,b],令a=(a+b)/2,重复循环;
- 如果f((a+b)/2)与f(b)同号,则说明根在区间[a,(a+b)/2],令b=(a+b)/2,重复循环。
本题目要求编写程序,计算给定3阶多项式f(x)=a3x3+a2x2+a1x+a0在给定区间[a,b]内的根。
输入格式:
输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0,在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。
输出格式:
在一行中输出该多项式在该区间内的根,精确到小数点后2位。
输入样例:
3 -1 -3 1
-0.5 0.5
输出样例:
0.33
#include <stdio.h>
double a3, a2, a1, a0; double f(double x)
{ double result; result=a3*x*x*x+a2*x*x+a1*x+a0; return result;
}int main()
{ double a, b; scanf("%lf%lf%lf%lf",&a3,&a2,&a1,&a0); scanf("%lf%lf",&a,&b); double left,mid,right; left=a; right=b; ///大于阈值时使用二分法求出单根,程序结束while(right-left>=0.001&&f(left)*f(right)<=0) { if(f(left)==0) { printf("%.2f",left); return 0; } if(f(right)==0) { printf("%.2f",right); return 0; } mid=(left+right)/2; if (f(mid)*f(left)>0) { left=mid; } else //由于先决条件为f(left)*f(right)<0,因此此时else语句等价于f(mid)与f(left)异号,即与f(right)同号{ right=mid; } } 不大于阈值时输出中点printf("%.2f",mid); return 0;
}
7-2 循环-十进制转化
小白龙新学了十进制的转换。现在他想把十进制数转化成其他进制的数,聪明的学弟学
妹们能帮帮他吗?因为小白龙还没有学习到数组,所以他希望这道题能够不用数组的相关知
识就可以解决。
输入格式:
输入只有两个整数N,M。 N ( 0 < N <= 100 ) 表示十进制数N。M( 2 <= M <= 9 )表示转换成M进制。
输出格式:
将N转化为M进制后然后输出。
输入样例:
在这里给出一组输入。例如:
50 4
输出样例:
在这里给出相应的输出。例如:
302
//题目暗示数组可以实现
#include <stdio.h>int main() {int n,m,a[100],i=0;scanf("%d%d",&n,&m);while(n){a[i++] =n%m; //从a[0]开始赋值n/=m;}while(i--){//逆序输出printf("%d",a[i]);}
}
7-3 梅森数
形如2n−1的素数称为梅森数(Mersenne Number)。例如2^2−1=3、23−1=7都是梅森数。1722年,双目失明的瑞士数学大师欧拉证明了231−1=2147483647是一个素数,堪称当时世界上“已知最大素数”的一个记录。
本题要求编写程序,对任一正整数n(n<20),输出所有不超过2n−1的梅森数。
输入格式:
输入在一行中给出正整数n(n<20)。
输出格式:
按从小到大的顺序输出所有不超过2n−1的梅森数,每行一个。如果完全没有,则输出“None”。
输入样例:
6
输出样例:
3
7
31
#include <stdio.h>
#include <math.h>int f(int x)//判断素数的函数
{for(int i=2;i<=sqrt(x);i++){if(x%i==0)return 0;//不是素数则返回0}return 1;
}int main()
{int n;scanf("%d",&n);if(n<=1)//n<=1时一定不存在梅森数printf("None"); else//n>=2时一定存在梅森数{for(int i=2;i<=n;i++){//对每一个2^i进行素数的判断int a=pow(2,i)-1;if(f(a)){printf("%d\n",a);}}}
}
7-4 单词长度
你的程序要读入一行文本,其中以空格分隔为若干个单词,以.结束。你要输出每个单词的长度。这里的单词与语言无关,可以包括各种符号,比如it's算一个单词,长度为4。注意,行中可能出现连续的空格;最后的.不计算在内。
输入格式:
输入在一行中给出一行文本,以.结束
**提示:**用scanf("%c",...);来读入一个字符,直到读到.为止。
输出格式:
在一行中输出这行文本对应的单词的长度,每个长度之间以空格隔开,行末没有最后的空格。
输入样例:
It's great to see you here.
输出样例:
4 5 2 3 3 4
如果题目要求不能出现连续的空格,以下代码是可行的:
#include <stdio.h>
int main()
{char c;int a=0;while((c=getchar())!='.'){if(c==' '){printf("%d ",a);a=0;}elsea++;}printf("%d",a);
}
但行中可能出现连续的空格,所以需要用一个标志变量来跟踪当前是否处于单词中的状态。
逻辑如下:
设count用于统计某单词的字符个数,mark用于标记是否遇到第一个空格,sum用于记录已经输出的单词个数。
如果当前字符不是空格,则将count加1
如果当前字符是空格并且count大于0,表示遇到一个单词的结束。如果mark大于0,说明不是第一个单词,先输出一个空格。输出统计得到的单词字符个数count。将sum加1,表示已经输出一个单词。将count重置为0,开始统计下一个单词的字符个数。将mark加1,表示已经遇到第一个空格。
循环结束后,判断最后一个单词是否有字符,如果有且sum大于0,输出最后一个单词的字符个数。
拿It's great to see you here.举例
初始状态:
count= 0sum= 0mark= 0
字符 ‘I’:
count= 1
字符 ‘t’:
count= 2
字符 ‘’':
count= 3
字符 ‘s’:
count= 4
字符 ’ ':
输出4
-
sgn=1 -
cnt= 0 -
mark= 1
字符 ‘g’:
cnt= 1
字符 ‘r’:
cnt= 2
字符 ‘e’:
cnt= 3
字符 ‘a’:
cnt= 4
字符 ‘t’:
cnt= 5
字符 ’ ':
输出空格再输出5
-
sgn=2 -
cnt= 0 -
mark= 2
字符 ‘t’:
cnt= 1
字符 ‘o’:
cnt= 2
字符 ’ ':
输出空格再输出2
-
sgn=3 -
cnt= 0 -
mark= 3
字符 ‘s’:
cnt= 1
字符 ‘e’:
cnt= 2
字符 ‘e’:
cnt= 3
字符 ’ ':
输出空格再输出3
-
sgn=4 -
cnt=0 -
mark= 4
字符 ‘y’:
cnt= 1
字符 ‘o’:
cnt= 2
字符 ‘u’:
cnt= 3
字符 ’ ':
输出空格再输出3
-
sgn=5 -
cnt= 0 -
mark= 5
字符 ‘h’:
cnt= 1
字符 ‘e’:
cnt= 2
字符 ‘r’:
cnt= 3
字符 ‘e’:
cnt= 4
字符 ‘.’:
此时cnt > 0 && sgn > 0,输出4
最终程序输出的结果是:4 5 2 3 3 4
#include <stdio.h>int main()
{char c;int count=0,mark=0,sum=0;while((c=getchar())!='.'){if(c!=' ')count++;else if(c==' '&&count>0){if(mark>0){printf(" ");}printf("%d",count);sum++;count=0;mark++;}}if(count>0&&sum>0){printf(" %d",count);}else if(count>0&&sum==0){printf("%d",count);}return 0;
}
7-5 21循环-求和3
sxtc爱做数学题,今天他又拿到一道数学题:

注意答案有可能很大,请对114514取模。
他希望擅长求和的你帮他解出这个求和问题。
输入格式:
读入两个数n,k。
输出格式:
输出求和结果,请对答案取模114514。
输入样例:
在这里给出一组输入。例如:
11451 4
输出样例:
在这里给出相应的输出。例如:
113968
思路:
1.使用两个嵌套的for循环,外层循环控制1到n的遍历,内层循环控制1到k的遍历。
2.在内层循环中,每次将total乘以当前外层循环的迭代变量i,并取结果对114514取模(%)。
3.在外层循环中,将计算得到的total累加到sum上,并将结果对114514取模,再重新将total置为1。
#include <stdio.h>
int main() {int n, k;scanf("%d%d", &n, &k);int total=1;int sum=0;for (int i=1;i<=n;i++) {for (int j=1;j<=k;j++) {total=(total*i)%114514;}sum =(sum+total)%114514;total=1;}printf("%d", sum);
}
7-6 21循环-金字塔
SeraphJACK正在摆积木。他想用这些积木垒成一座金字塔。同时摆好金字塔之后,他为每层积木涂上不同的颜色,这些颜色用从1开始的正整数表示,从最底层开始涂色。现在告诉你SeraphJACK有n块积木,请输出他用这些积木能摆出并涂色的最大金字塔。(金字塔形状详见样例,0表示这个位置没有积木)
输入格式:
一个整数n,1<=n<=1000
输出格式:
涂色后的金字塔
输入样例1:
在这里给出一组输入。例如:
11
输出样例1:
在这里给出相应的输出。例如:
0004000
0030300
0202020
1010101
输入样例2:
在这里给出一组输入。例如:
1
输出样例2:
在这里给出相应的输出。例如:
1
#include<stdio.h>
int main()
{int sum,n,c=1,d;scanf("%d",&sum);for(n=1;n*(n+1)/2<=sum;n++);while(c<=(n-1))//外层循环控制层数{d=1;while(d<=2*n-3)//内层循环控制涂色及编号{if(d<=(n-1-c)||d>n-2+c)printf("0");//如果位置d小于等于(n-1-c),或者大于n-2+c,则打印0。else if((d-n+1+c)%2==1)printf("%d",n-c);//否则,如果(d-n+1+c)除以2的余数为1,则打印n-c,表示涂上对应颜色的编号。else printf("0");//否则,打印0。d++;}printf("\n");c++;}return 0;
}
7-7 循环-杨辉三角
Little VayH_E带着他的小伙伴玩起了杨辉三角的游戏…

输入格式:
输入包含两个正整数n和m(1<=n,m<=20),两个数之间用空格分开。
输出格式:
输出杨辉三角的第n行与第m行之间(包含第n,m行)的部分,输出时注意:
倒数第一行的第一个数字前有0个空格…倒数第k行(如果有的话)的第一个数字前有k-1个空格…以此类推
每一行的每两个数字(如果有的话)之间有1个空格
每一行的最后一个数字后没有空格,在每一行的最后一个数字后输出一个换行符
对于所求的杨辉三角,每一个数字都只取最后一位,例如,若所求的杨辉三角上某个数字为10,则应输出0
输入样例:
在这里给出一组输入。例如:
1 4
输出样例:
在这里给出相应的输出。例如:
11 11 2 1
1 3 3 1
#include <stdio.h>
int main()
{long int n,m,i,k,a,b,c,d,e,f,t;scanf("%ld %ld",&n,&m);if(n>m){t=n;n=m;m=t;}for(i=n;i<=m;i++)//对于每行而言{for(k=m-i+1;k>1;k--){printf(" ");//循环输出每行前面的空格}printf("1");for(a=1;a<=i-2;a++)//输出第i行的第二个到倒数第二个数{c=1;e=1;for(b=i-1;b>=i-a;b--){c=c*b;}for(d=a;d>=1;d--){e=e*d;}f=(c/e)%10;printf(" %ld",f);}if(i==1)printf("\n");//第一行输出回车elseprintf(" 1\n");//输出每行的最后一个1和回车}return 0;
}
相关文章:

【C/PTA】循环结构进阶练习(二)
本文结合PTA专项练习带领读者掌握循环结构,刷题为主注释为辅,在代码中理解思路,其它不做过多叙述。 7-1 二分法求多项式单根 二分法求函数根的原理为:如果连续函数f(x)在区间[a,b]的两个端点取值异号,即f(a)f(b)<0…...
Visual Studio 2010 软件安装教程(附下载链接)——计算机二级专用编程软件
下载链接: 提取码:2wAKhttps://www.123pan.com/s/JRpSVv-9injv.html 安装步骤如下: 1.如图所示,双击打开【Visual Studio 2010简体中文旗舰版】文件夹 2.如图所示,找到“Setup”文件夹打开,双击运行“setup” 3.如图…...

大促来袭 零点价格如何监测
双十一大促即将到来,各大品牌、店铺都会非常关注价格,这个时候的促销信息会很复杂,平台促销、店铺促销等,不同的优惠信息涉及的券也会很多,同时各优惠券关联的时间点也会不同,有些券零点能用,有…...

python 之 正则表达式模块re
文章目录 findall例子:特点和注意事项: match示例:match 对象的方法和属性:注意事项: search示例:match 对象的方法和属性:注意事项: split示例:参数说明:注意…...
vue项目npm install报错解决
一、报错信息 node-sass4.14.1 postinstall: node scripts/build.js 二、解决方式 (1)删除未成功安装的 node_modules 文件; (2)为 node-sass 单独设置镜像源; npm config set sass_binary_sitehttps:/…...

ubuntu挂载共享目录的方法
ubuntu挂载共享目录的方法 安装NFS配置NFS 安装NFS sudo apt-get install nfs-kernel-server配置NFS 创建work共享目录:(本人将此文件放在桌面)sudo mkdir worksudo gedit /etc/exports添加: /home/zynq/Desktop/work *(rw,sync,no_root_squash,no_subtree_check)运行以下命…...
累计概率分布、概率分布函数(概率质量函数、概率密度函数)、度量空间、负采样(Negative Sampling)
这里写自定义目录标题 机器学习的基础知识累计概率分布概率分布函数度量空间负采样(Negative Sampling)基于分布的负采样(Distribution-based Negative Sampling):基于近邻的负采样(Neighbor-based Negativ…...

〔001〕虚幻 UE5 安装教程
✨ 目录 🎈 下载启动程序🎈 注册个人账户🎈 选择引擎版本🎈 选择安装选项🎈 虚幻商城的使用🎈 每月免费插件🎈 安装插件🎈 下载启动程序 下载地址:https://www.unrealengine.com/zh-CN/download点击上面地址,下载 UE5 启动程序并安装🎈 注册个人账户 打开商…...

Crypto(8) BUUCTF-bbbbbbrsa1
题目描述: from base64 import b64encode as b32encode from gmpy2 import invert,gcd,iroot from Crypto.Util.number import * from binascii import a2b_hex,b2a_hex import randomflag "******************************"nbit 128p getPrime(nbit)…...
软件测试之随机测试详解
在软件测试中除了根据测试用例和测试说明书进行功能测试外,还需要进行随机测试,随机测试是没有书面测试用例、记录期望结果、检查列表、脚本或指令的测试。主要是根据测试者的经验对软件进行功能和性能抽查。随机测试是根据测试说明书执行测试用例的重要…...

【广州华锐互动】3D全景虚拟旅游在文旅行业的应用场景
随着科技的不断发展,3D全景虚拟旅游正在成为一种新兴的旅游体验方式,它可以帮助旅游者更加深入地了解旅游信息,提升旅游体验。下面我们将详细介绍3D全景虚拟旅游可以应用于哪些场景。 一、旅游规划 3D全景虚拟旅游可以帮助旅游者更加直观地进…...
多目标跟踪算法 实时检测 - opencv 深度学习 机器视觉 计算机竞赛
文章目录 0 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习多目标跟踪 …...

深入了解Jedis:Java操作Redis的常见类型数据存储
目录 前言 一、Jedis介绍 1.Jedis在各方面的功能 2.特点 二、Java连接Redis 1.导入pom依赖 2.建立连接 三、Java操作Redis的常见类型数据存储 1.字符串 2.哈希表 3.列表 4.集合 5.有序集合 四、Redis的实际应用场景实例 1.会议信息实体 2.自定义注解 3.创建切面…...

angular+ionic+npm项目运行
angularionicnpm项目运行 错误记录(1)Downloading binary from https://github.com/sass/node-sass/releases/download/v4.14.1/win32-x64-72_binding.node(2)The npm warning "A requires a peer of B but none is installe…...

【数据库】数据库模式 Schema
数据库模式 Schema 1.MySQL2.PostgreSQL3.SQL Server4.Oracle5.SQLite 在数据库的术语中,模式(schema)是一个逻辑概念,用于组织数据库中的对象。模式中的对象通常包括 表、索引、数据类型、序列、视图、存储过程、主键、外键 等等…...
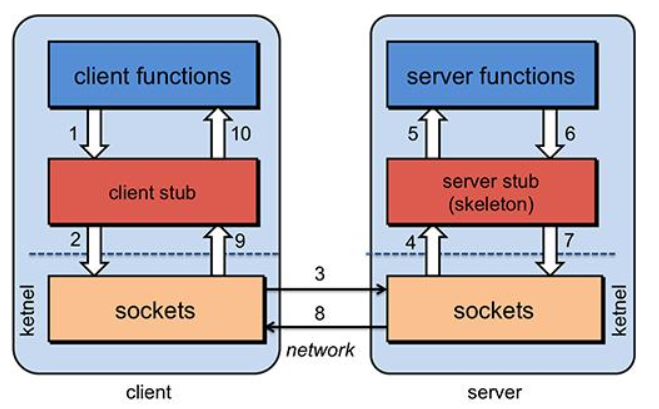
RPC 原理详解
文章目录 什么是 RPCRPC 基本原理RPC核心功能服务寻址数据编解码网络传输一次RPC的调用过程 实践基于HTTP协议的RPC基于TCP协议的RPC 什么是 RPC RPC(Remote Procedure Call),即远程过程调用,它允许像调用本地服务一样调用远程服…...
新版Helix QAC 100%覆盖MISRA C++:2023
Helix QAC 2023.3预期将100%覆盖在2023年第四季度发布的新的MISRA C:2023规则。 此外,该版本支持更多的C20语言特性,并改进了Perforce Validate平台和Helix QAC与Validate的集成,以及其他质量改进。 编码标准覆盖率(MISRA C:202…...

maven 项目添加 git-hook 脚本,约束提交内容格式
git 提交代码,推送代码,可以通过在 .git/hooks 目录中的 bash 脚本来做一定的验证工作。 本例使用插件 maven-antrun-plugin 自动输出脚本至 .git/hooks 目录中,在 pom.xml 中的使用示例如下: <plugin><groupId>org.…...

18、Flink的SQL 支持的操作和语法
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

泛微OA_lang2sql 任意文件上传漏洞复现
简介 泛微OA E-mobile系统 lang2sql接口存在任意文件上传漏洞,由于后端源码中没有对文件没有校验,导致任意文件上传。攻击者可利用该参数构造恶意数据包进行上传漏洞攻击。 漏洞复现 FOFA语法: title"移动管理平台-企业管理" 页…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
