VMware网络设置 桥接模式 NAT VMNET0 1 8
1.桥接模式
虚拟机与主机并列 可拥有独立IP
主机与虚拟机之间，以及各虚拟机之间都可以互访。对应虚拟机就被当成主机所在以太网上的一个独立物理机来看待，各虚拟机通过默认的 VMnet0 网卡与主机以太网连接，虚拟机间的虚拟网络为 VMnet0。这时你的虚拟机就像局域网中的一个独立的物理机一样。虚拟机中的操作系统可以 PING 别的主机，反过来别的主机也可以 PING 虚拟机。
2.NAT模式
NAT模式上网设置较简单
NAT模式和桥接模式一样可以上网，只不过，虚拟机会虚拟出一个内网，主机和虚拟机都在这个虚拟的局域网中。NAT中VMWare相当于交换机（产生一个局域网，在这个局域网中分别给主机和虚拟机分配ip地址）。虚拟机通过宿主机器所在的网络来访问公网。
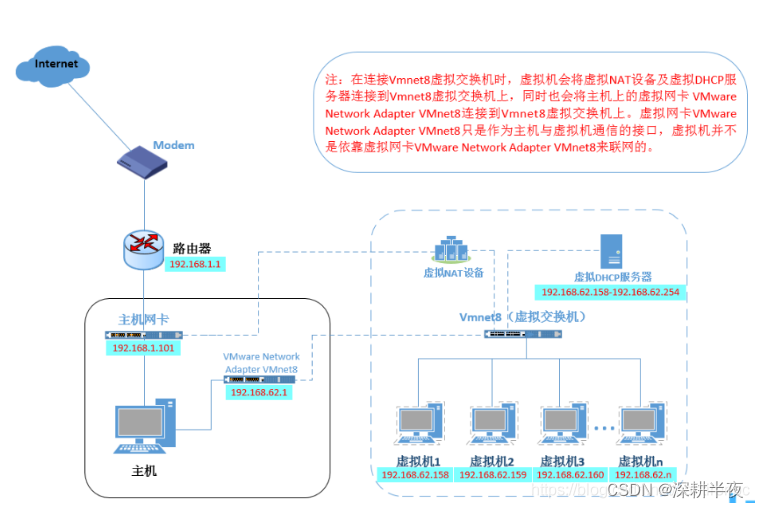
3.桥接 NAT区别
桥接模式 有独立IP
NAT（网络地址转换）模式的设置比桥接简单；桥接模式设置复杂，并且有些情况不得不用，有些情况又不能用； 一般没有特殊需求只是为了上网，选择NAT模式最简单 ；
4.VMnet0 VMnet1 VMnet8 区别
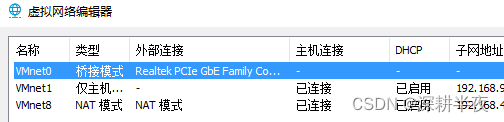
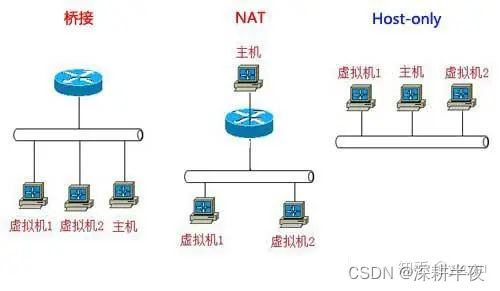
①Adapter=VMnet1=eth0(host-only)
虚拟机之间、主机与虚拟机之间互访，但虚拟机无法访问外网。
②Adapter2=VMnet8=eth8(nat)
虚拟机之间、主机与虚拟机之间互访，虚拟机可以通过主机访问外网，外网无法访问虚拟机
③Adapter3=VMnet0=eth2(Bridged)
虚拟机相当于一台实体机，可以自由访问与被访问及上网
部分图来自
“桥接”和“NAT”方式区别 - 知乎 (zhihu.com)
相关文章：
VMware网络设置 桥接模式 NAT VMNET0 1 8
1.桥接模式 虚拟机与主机并列 可拥有独立IP 主机与虚拟机之间，以及各虚拟机之间都可以互访。对应虚拟机就被当成主机所在以太网上的一个独立物理机来看待，各虚拟机通过默认的 VMnet0 网卡与主机以太网连接，虚拟机间的虚拟网络为 VMnet0。这…...
【MongoDB】MongoExport如何过滤数据导出
问题 使用MongoDB处理导出数据时，想增加数据过滤操作。 例如：导出所有isGirl为true的所有数据。 分析 在mongoexport说明文档中找到了query字段和queryFile字段，用来进行数据查询匹配导出。 query字段 后面直接跟 json格式数据。 queryF…...
吴恩达《机器学习》6-1-＞6-3:分类问题、假设陈述、决策界限
一、什么是分类问题？ 在分类问题中，我们试图预测的变量𝑦是离散的值，通常表示某种类别或标签。这些类别可以是二元的，也可以是多元的。分类问题的示例包括： 判断一封电子邮件是否是垃圾邮件（二…...
C语言 用字符串比较函数cmp来做一个门禁：账号密码是否匹配 （干货满满）
#include<stdio.h> #include<string.h> void fun04() {for (int i 0; i < 3; i){char *str01 "hello";char uname[100] ;printf("请输入账号");scanf("%s",uname);char *str02 "123456";char pword[100];printf(&qu…...
Uniapp实现多语言切换
前言 之前做项目过程中，也做过一次多语言切换，大致思想都是一样的，想了解的可以看下之前的文章C#WinForm实现多语言切换 使用i18n插件 安装插件 npm install vue-i18n --saveMain.js配置 // 引入 多语言包 import VueI18n from vue-i18n…...
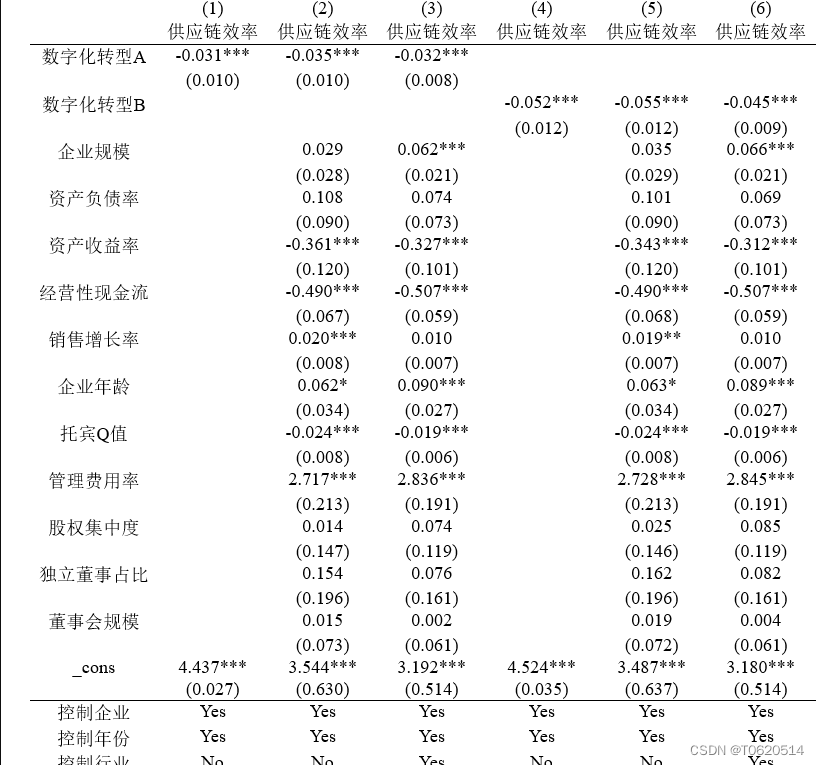
企业数字化转型与供应链效率-基准回归复刻（2007-2022年）
参照张树山（2023）的做法，本团队对来自统计与决策《企业数字化转型与供应链效率》一文中的基准回归部分进行复刻。文章实证检验企业数字化转型对供应链效率的影响。用年报词频衡量上市公司数字化转型程度，以库存周转天数来衡量供应…...
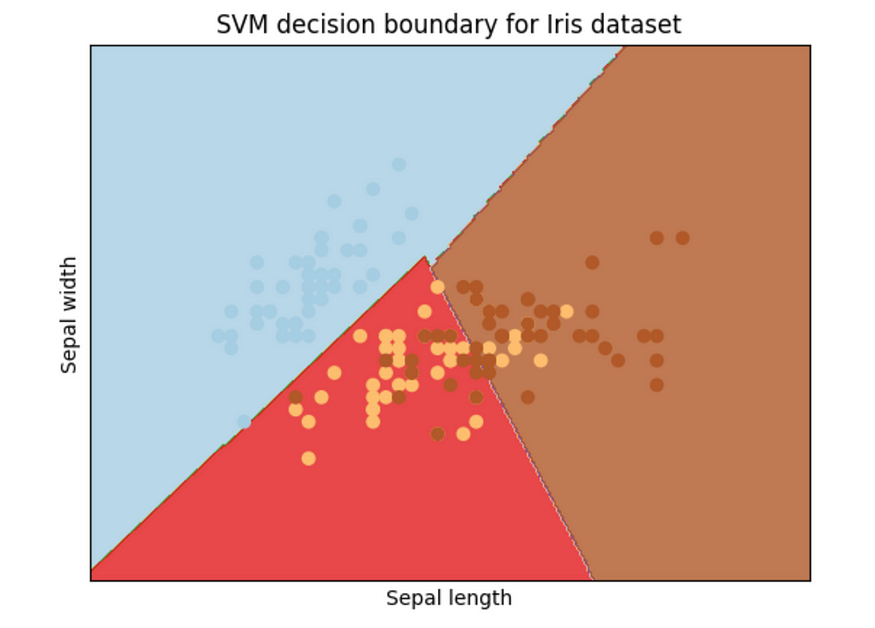
支持向量机 (SVM)：初学者指南
照片由 Unsplash上的 vackground.com提供 一、说明 SVM（支持向量机）简单而优雅用于分类和回归的监督机器学习方法。该算法试图找到一个超平面，将数据分为不同的类，并具有尽可能最大的边距。本篇我们将介绍如果最大边距不存在的时候…...
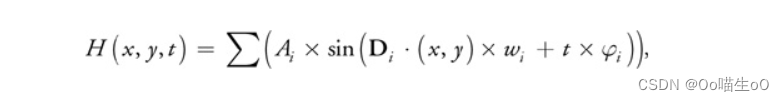
UnityShader(五)
这次要用表面着色器实现一个水的特效。先翻到最下边看代码，看不懂再看下面的解释。 首先第一步要实现水的深浅判断，实现深水区和浅水区的区分。 这里需要用到深度图的概念。不去说太多概念，只去说怎么实现的，首先我们的水面是在…...
Java中的类和对象
文章目录 一、类和对象的基本概念二、类和对象的定义和使用1.创建类的语法2.创建类的对象3.范例(创建一个类的对象) 三、this引用1.什么是this引用2.this引用的特性 四、构造方法五、封装1.封装的概念2.访问限定符3.封装扩展包3.1包的概念3.2常见的包 六、static成员1.static修…...
多测师肖sir_高级金牌讲师_jenkins搭建
jenkins操作手册 一、jenkins介绍 1、持续集成（CI） Continuous integration 持续集成 团队开发成员每天都有集成他们的工作，通过每个成员每天至少集成一次，也就意味着一天有可 能多次集成。在工作中我们引入持续集成，通…...
Ps：色彩范围
Ps菜单：选择/色彩范围 Select/Color Range 色彩范围 Color Range是一个功能强大选择命令，不仅可以基于颜色进行选择，而且可以基于影调进行选择。不仅可以用来检测人脸选择肤色，也可用来选择超出印刷色域范围的区域。 在图层蒙版的…...
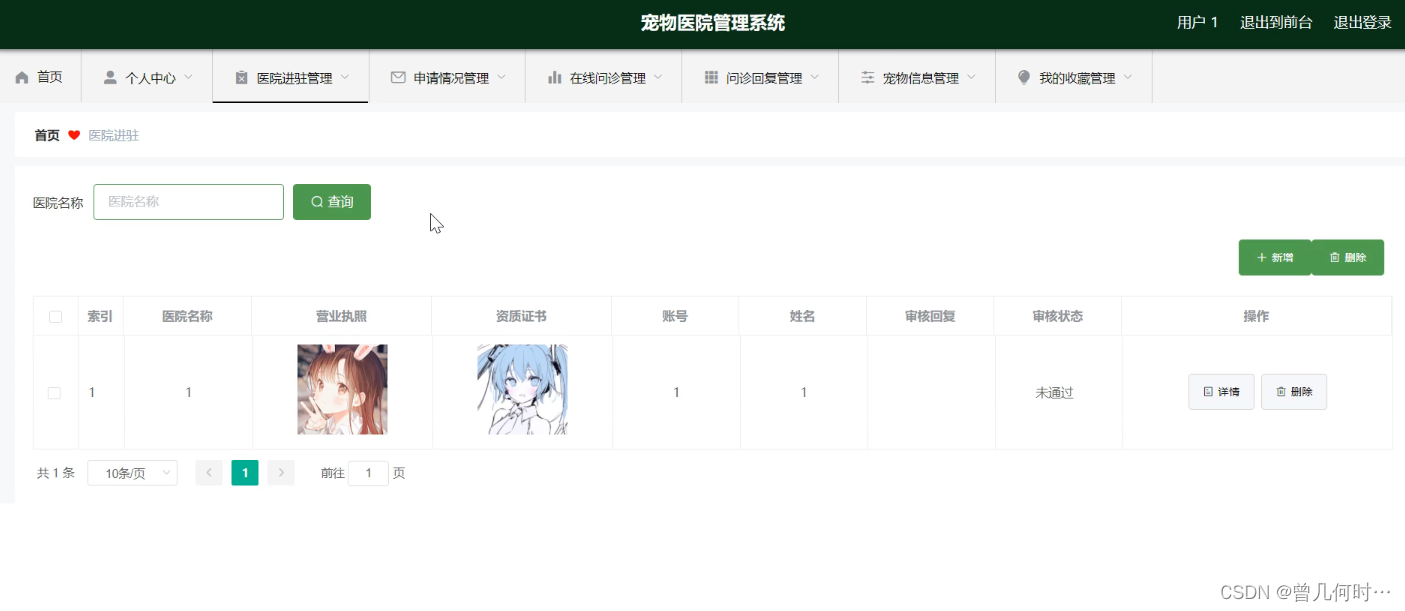
基于SSM的宠物医院管理系统
末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SSM 前端：Vue 数据库：MySQL5.7和Navicat管理工具结合 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否Maven项目：是 目录…...
华为政企园区网络交换机产品集
产品类型产品型号产品说明 核心/汇聚交换机CloudEngine S5731-H24P4XCCloudEngine S5731-H24P4XC 提供 24个10/100/1000BASE-T以太网端口，4个万兆SFP，CloudEngine S5731-H 系列交换机是华为公司推出的新一代智能千兆交换机，基于华为公司统…...
NVMe FDP会被广泛使用吗？
文章开头，我们需要先了解固态硬盘的读写机制。我们知道，固态硬盘的存储单元是由闪存颗粒组成的，无法实现物理性的数据覆盖，只能擦除然后写入，重复这一过程。因而，我们可以想象得到，在实际读写过…...
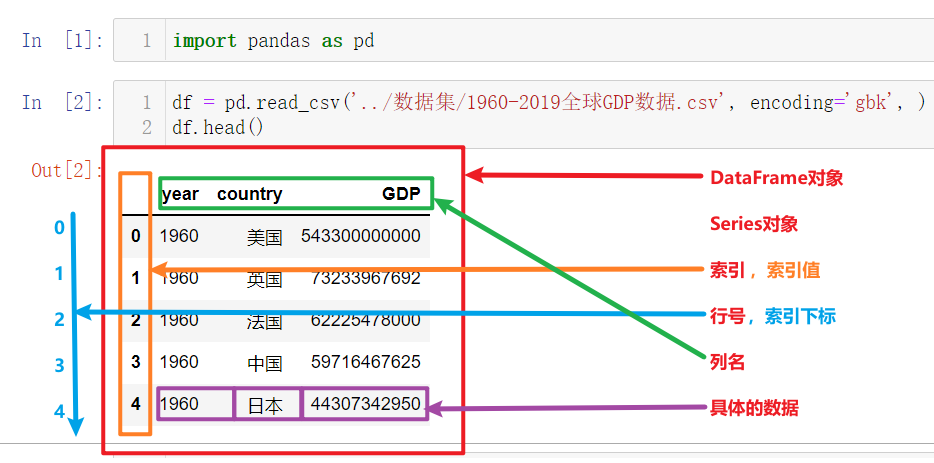
[黑马程序员Pandas教程]——Pandas数据结构
目录： 学习目标认识Pandas中的数据结构和数据类型Series对象通过numpy.ndarray数组来创建通过list列表来创建使用字典或元组创建s对象在notebook中不写printSeries对象常用API布尔值列表获取Series对象中部分数据Series对象的运算DataFrame对象创建df对象DataFrame…...
AI 绘画 | Stable Diffusion 提示词
Prompts提示词简介 在Stable Diffusion中，Prompts是控制模型生成图像的关键输入参数。它们是一种文本提示，告诉模型应该生成什么样的图像。 Prompts可以是任何文本输入，包括描述图像的文本，如“一只橘色的短毛猫，坐在…...
tomcat默认最大线程数、等待队列长度、连接超时时间
tomcat默认最大线程数、等待队列长度、连接超时时间 tomcat的默认最大线程数是200，默认核心线程数(最小空闲线程数)是10。 在核心线程数满了之后，会直接启用最大线程数（和JDK线程池不一样，JDK线程池先使用工作队列再使用最大线程…...
本地部署 CogVLM
本地部署 CogVLM CogVLM 是什么CogVLM Github 地址部署 CogVLM启动 CogVLM CogVLM 是什么 CogVLM 是一个强大的开源视觉语言模型（VLM）。CogVLM-17B 拥有 100 亿视觉参数和 70 亿语言参数。 CogVLM-17B 在 10 个经典跨模态基准测试上取得了 SOTA 性能&am…...
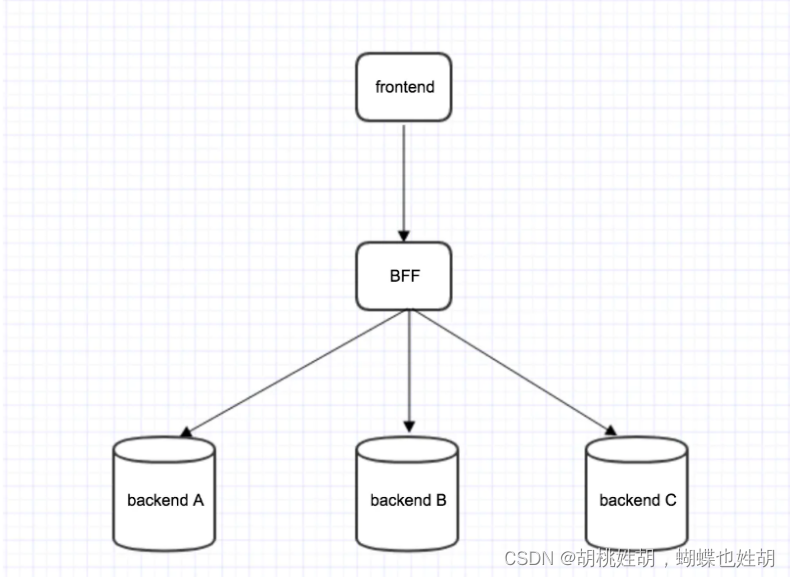
bff层解决了什么痛点
bff层 -- 服务于前端的后端 什么是bff？ Backend For Frontend（服务于前端的后端），也就是服务器设计API的时候会考虑前端的使用，并在服务端直接进行业务逻辑的处理，又称为用户体验适配器。BFF只是一种逻辑…...
面试经典150题——Day33
文章目录 一、题目二、题解 一、题目 76. Minimum Window Substring Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there …...
逻辑回归：给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告（肿瘤大小、血液指标），你需要做出一个**决定性判断**：恶性还是良性？这种“非黑即白”的抉择，正是**逻辑回归（Logistic Regression）** 的战场&a…...
蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡，轻快的音乐在耳边持续回荡，小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下，六一来了。 今天是六一儿童节，小蓝老师为了让大家在节…...
三体问题详解
从物理学角度，三体问题之所以不稳定，是因为三个天体在万有引力作用下相互作用，形成一个非线性耦合系统。我们可以从牛顿经典力学出发，列出具体的运动方程，并说明为何这个系统本质上是混沌的，无法得到一般解…...
RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程
本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习视频及资料，尽在聚客AI学院。 本文全面剖析RNN核心原理，深入讲解梯度消失/爆炸问题，并通过LSTM/GRU结构实现解决方案，提供时间序列预测和文本生成…...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
API网关Kong的鉴权与限流：高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填！ 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中，API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关，Kong凭借其插件化架构…...
在golang中如何将已安装的依赖降级处理，比如：将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤： 第一步： 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为： // 改为 v…...
CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点： 共 6 个字段： Year（年）Month（月）Day（日）Hour（小时）Minute（分钟）Second（秒） 表示…...
CTF show 数学不及格
拿到题目先查一下壳，看一下信息 发现是一个ELF文件，64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断，第一个argc ! 5这个判断并没有起太大作用，主要是下面四个if判断 根据题目…...
【题解-洛谷】P10480 可达性统计
题目：P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图，分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M，接下来 M M M 行每行两个整数 x , y x,y x,y，表示从 …...