六大排序算法:插入、选择、冒泡、快排、希尔、归并
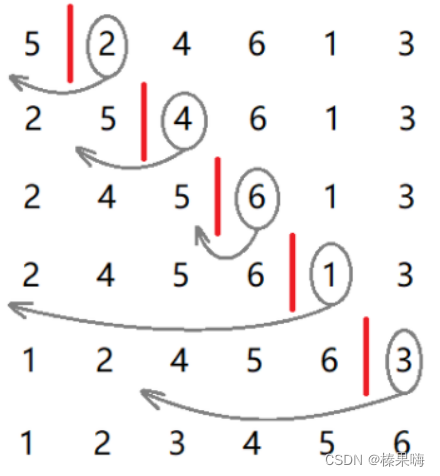
1、插入排序
解析:第一个元素设定为已经排好序,依次选择后续的元素插入到已经排好序的组内进行排序。
图示:
代码:
public static void insertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;// 将比当前元素大的元素向右移动while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}// 插入当前元素到正确的位置arr[j + 1] = key;}}时间复杂度:最坏情况下为O(N^2),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
2、选择(比较)排序:
解析:每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完。
图示:
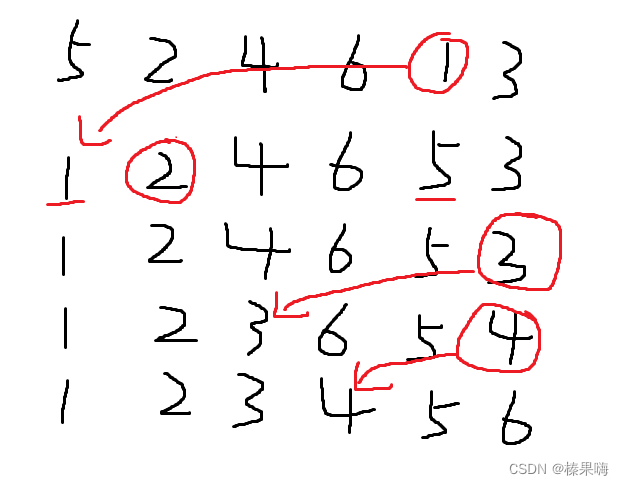
代码:
public static void selectionSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {int minIndex = i;// 寻找未排序部分的最小元素的索引for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 将找到的最小元素与未排序部分的第一个元素交换int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}时间复杂度:最坏情况:O(N^2)
最好情况:O(N^2)
空间复杂度:O(1)
3、冒泡排序
解析:左边大于右边交换,一趟排下来最大的在右边
图示:
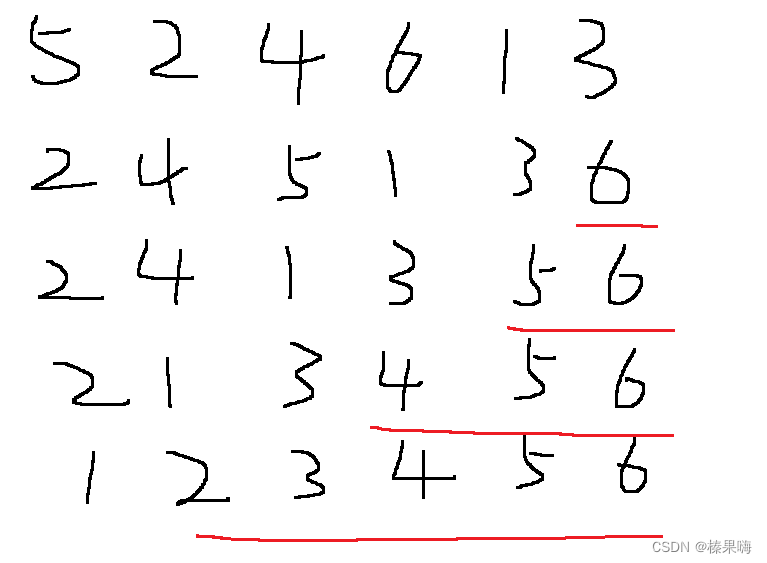
代码:
public static void bubbleSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]和arr[j + 1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}时间复杂度:最坏情况:O(N^2)
最好情况:O(N)
空间复杂度:O(1)
4、快排
解析:
- 1.先从数列中取出一个数作为基准数。
- 2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 3.再对左右区间重复第二步,直到各区间只有一个数或者这个区间不存在。
图示:
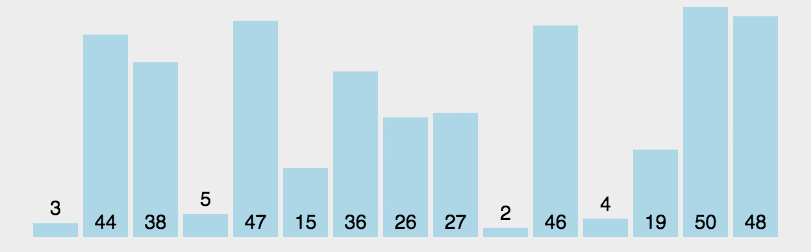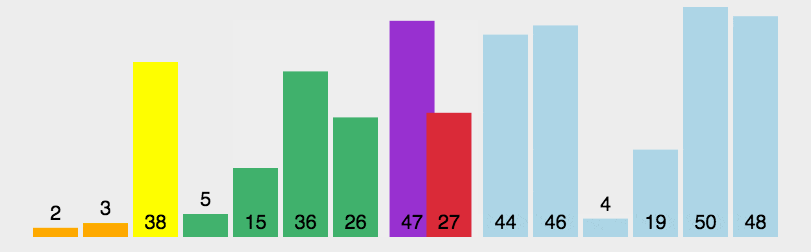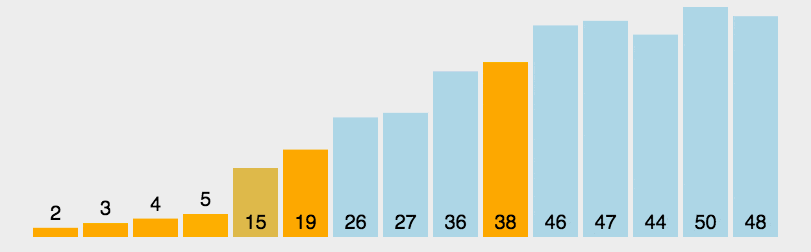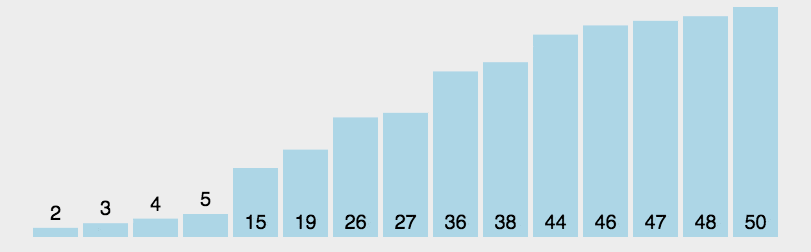
代码:
public static void quickSort(int[] arr, int low, int high) {if (low < high) {// 划分数组,返回分区点的索引int pivotIndex = partition(arr, low, high);// 递归排序分区左侧和右侧的子数组quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);}}public static int partition(int[] arr, int low, int high) {int pivot = arr[high]; // 选择最后一个元素作为基准元素int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;// 交换arr[i]和arr[j]int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}// 将基准元素放到正确的位置int temp = arr[i + 1];arr[i + 1] = arr[high];arr[high] = temp;return i + 1;}时间复杂度:O(NlogN)
空间复杂度:O(1)
5、希尔排序
解析:
1.先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
图示:
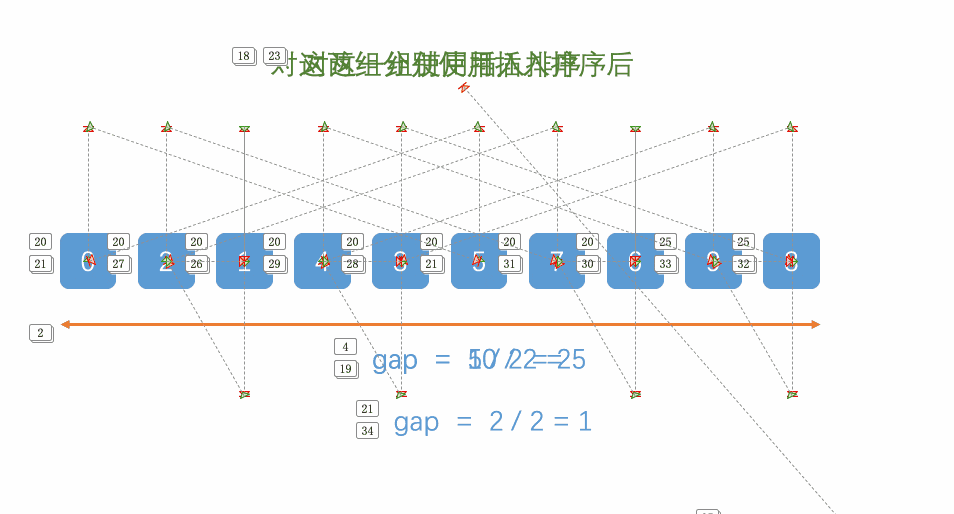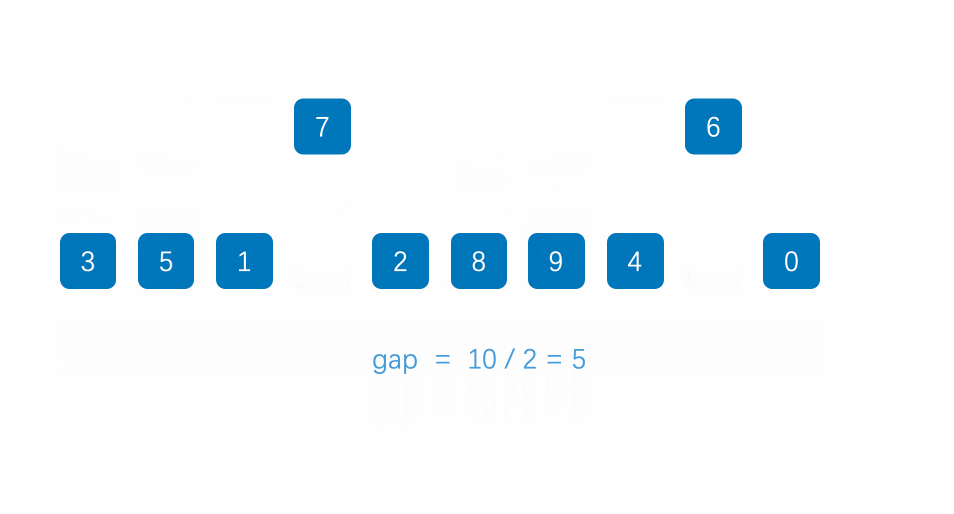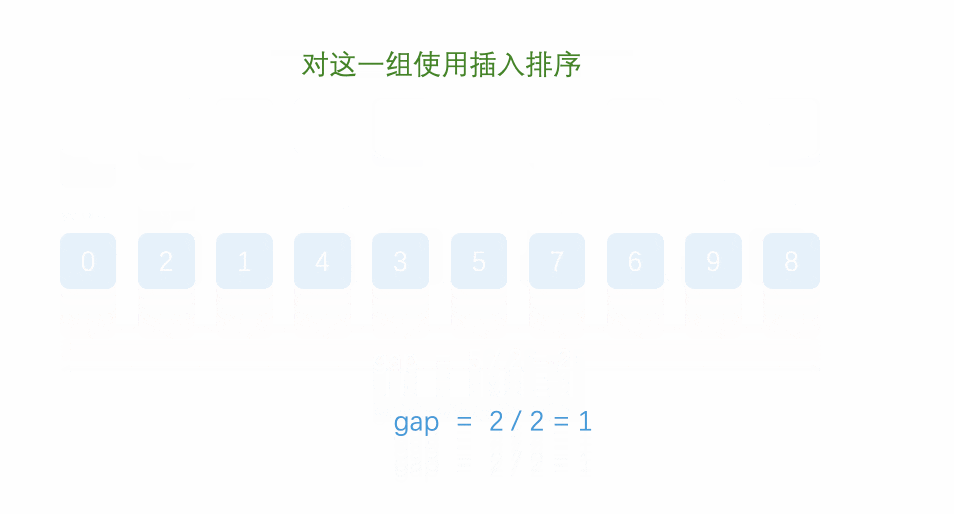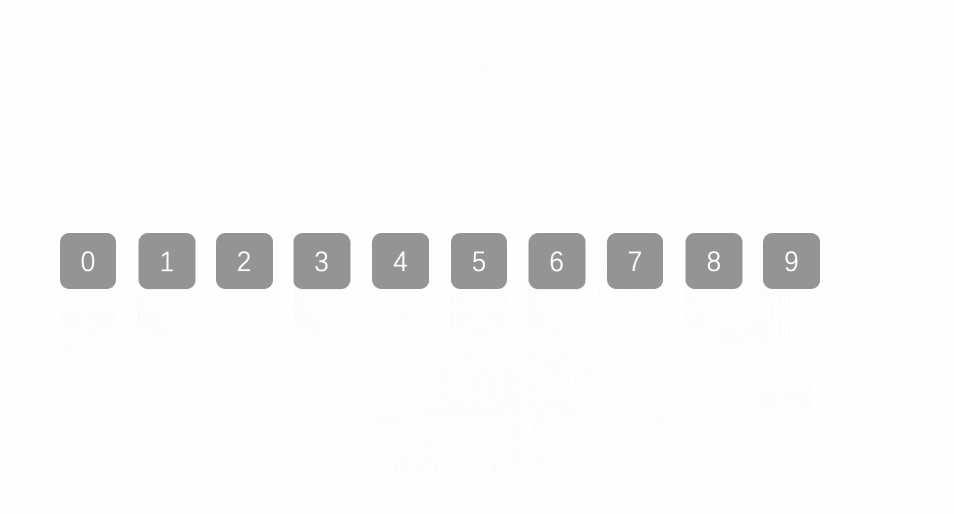
代码:
public static void shellSort(int[] arr) {int n = arr.length;// 初始间隔设为数组长度的一半,然后逐渐缩小间隔for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}}时间复杂度平均:O(N)
空间复杂度:O(1)
6、归并排序
解析:
- 将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
- 将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表
图示:
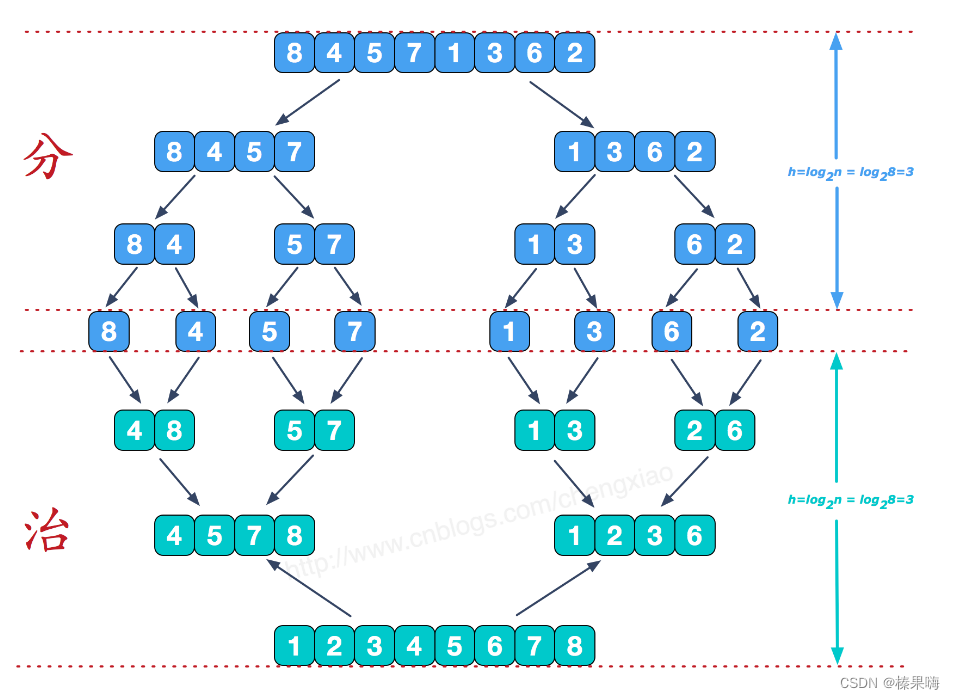
代码:
public static void mergeSort(int[] arr) {int n = arr.length;if (n <= 1) {return; // 如果数组长度小于等于1,无需排序}// 将数组分成两个子数组int mid = n / 2;int[] left = new int[mid];int[] right = new int[n - mid];System.arraycopy(arr, 0, left, 0, mid);System.arraycopy(arr, mid, right, 0, n - mid);// 递归排序左右子数组mergeSort(left);mergeSort(right);// 合并两个有序子数组merge(arr, left, right);}public static void merge(int[] arr, int[] left, int[] right) {int n1 = left.length;int n2 = right.length;int i = 0, j = 0, k = 0;while (i < n1 && j < n2) {if (left[i] <= right[j]) {arr[k] = left[i];i++;} else {arr[k] = right[j];j++;}k++;}while (i < n1) {arr[k] = left[i];i++;k++;}while (j < n2) {arr[k] = right[j];j++;k++;}}时间复杂度平均:O(N)
空间复杂度:O(N)
相关文章:

六大排序算法:插入、选择、冒泡、快排、希尔、归并
1、插入排序 解析:第一个元素设定为已经排好序,依次选择后续的元素插入到已经排好序的组内进行排序。 图示: 代码: public static void insertionSort(int[] arr) {int n arr.length;for (int i 1; i < n; i) {int key a…...
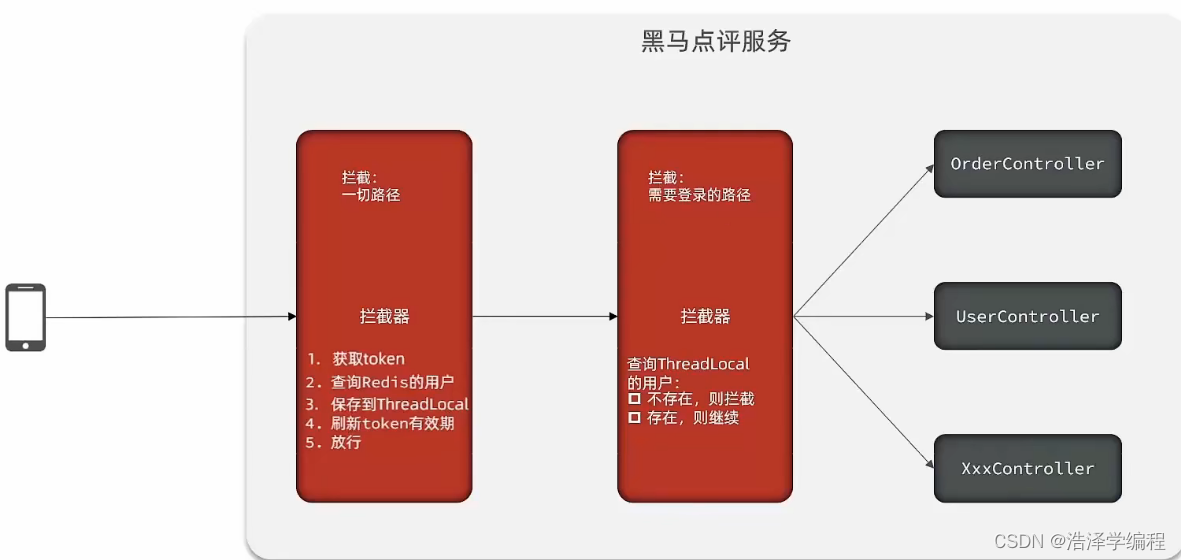
短信登录实现(黑马点评为例)
文章目录 前言一、隐藏用户敏感信息二、短信验证登录、注册1.流程2.代码3.使用redis优化解决代码 二、登录拦截(校验)1.流程2.代码 总结 前言 短信登录核心知识 首先黑马点评这个短信登录是一伪验证,即后台调用工具类随机生成六位数字。 1.R…...

【uniapp】签名组件,兼容vue2vue3
网上找了个源码改吧改吧,清除了没用的功能和兼容性,基于uniapp开发的 样子 vue2 使用方法,具体的可以根据业务自行修改 <signature ref"signature" width"100%" height"410rpx"></signature>confi…...
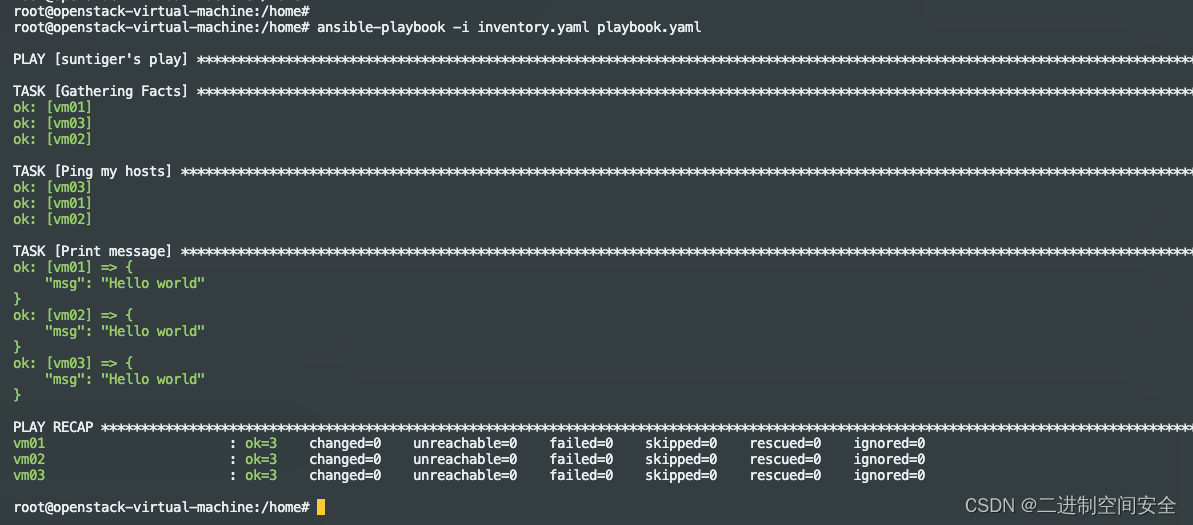
初步利用Ansible实现批量服务器自动化管理
1.Ansible介绍 Ansible是一款开源的自动化运维工具, 在2012年由Michael DeHaan创建, 现在由Red Hat维护。Ansible是基于Python开发的,采用YAML语言编写自动化脚本playbook, 可以在Linux、Unix等系统上运行, 通过SSH协议管理节点, 无需在被管理节点安装agent。Ansible以其简单、…...

网络安全和隐私保护技术
一、定义 网络安全和隐私保护技术是指在互联网和其他网络环境中,通过技术手段保护网络系统、网络数据和用户隐私免于受到恶意攻击、非法访问、窃取或滥用。网络安全和隐私保护技术是保护网络安全和用户隐私的重要手段,是保障互联网和其他网络环境正常运…...
)
保险行业采购管理痛点及解决方案(数智化采购系统)
随着社会发展,个人和企业有了更多的金融保险需求。对于金融保险公司而言,需要在采购合规的基础上,基于数智化能力,让经营变得更加高效和智能。 1、围绕重点领域,业务加速布局。 保险行业结合自身业务经营重点&#x…...
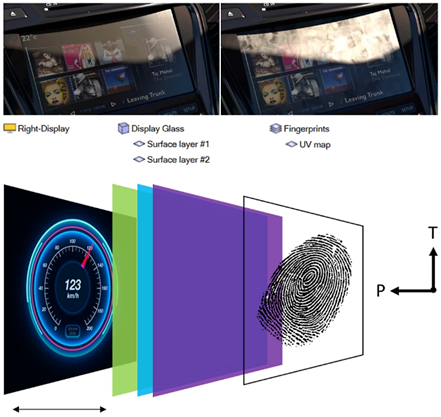
光学仿真 | 仿真推动以人类视觉感知为本的汽车显示设计
如果产品设计无法使终端用户产生共鸣,就不会存在卓越的工程设计。您可以设计一种结构坚固的方向盘,但如果它被放在错误的位置,就无法实现其用于转向的主要目的。 同样,在围绕人类视觉进行设计时,显示器其实无需具备尽…...
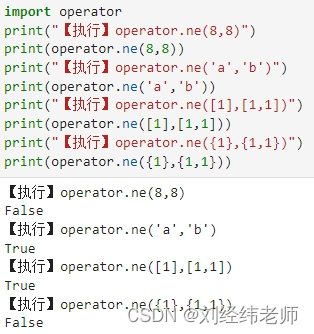
判断两个对象是否不相等operator.ne()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断两个对象是否不相等 operator.ne() 选择题 下列代码执行输出的结果是? import operator print("【执行】operator.ne(8,8)") print(operator.ne(8,8)) print("【执行】…...

2023年云计算发展趋势:生活的智能未来
目录 引言1 智能家居的崭新时代2 无人驾驶的崭新时代3 虚拟现实的扩展与改进4 人工智能的综合应用5 云计算的可持续性结语 引言 时光荏苒,科技的飞速发展已经成为当今社会的标志之一。在这个数字化时代,云计算已经成为推动技术革新和生活方式改变的关键…...

Spring Boot项目中通过 Jasypt 对属性文件中的账号密码进行加密
下面是在Spring Boot项目中对属性文件中的账号密码进行加密的完整步骤,以MySQL的用户名为root,密码为123321为例: 步骤1:引入Jasypt依赖 在项目的pom.xml文件中,添加Jasypt依赖: <dependency><…...

2.3 矩阵消元
一、消元矩阵 消元矩阵执行消元步骤用到的矩阵。从第 i i i 个方程减去 l i j l_{ij} lij 乘第 j j j 个方程(将 x j x_j xj 从第 i i i 行中消去)。我们需要很多个简单的矩阵 E i j E_{ij} Eij,每一个对应一个主对角线下方要消…...

Docker 从构建开始导出一个镜像
docker build docker build命令用于从Dockerfile创建一个镜像。它的基本格式如下: docker build [OPTIONS] PATH | URL | -这里的PATH是Dockerfile所在的路径,URL是一个Git仓库地址,-表示从标准输入读取Dockerfile。 docker build命令的一…...

案例研究|腾讯音乐娱乐集团与JumpServer共探安全运维审计解决方案
近年来,得益于人民消费水平的提升以及版权意识的加强,用户付费意愿和在线用户数量持续增长,中国在线音乐市场呈现出稳定增长的发展态势。随着腾讯音乐于2018年12月上市,进一步推动了中国在线音乐市场的发展。 腾讯音乐娱乐集团&a…...
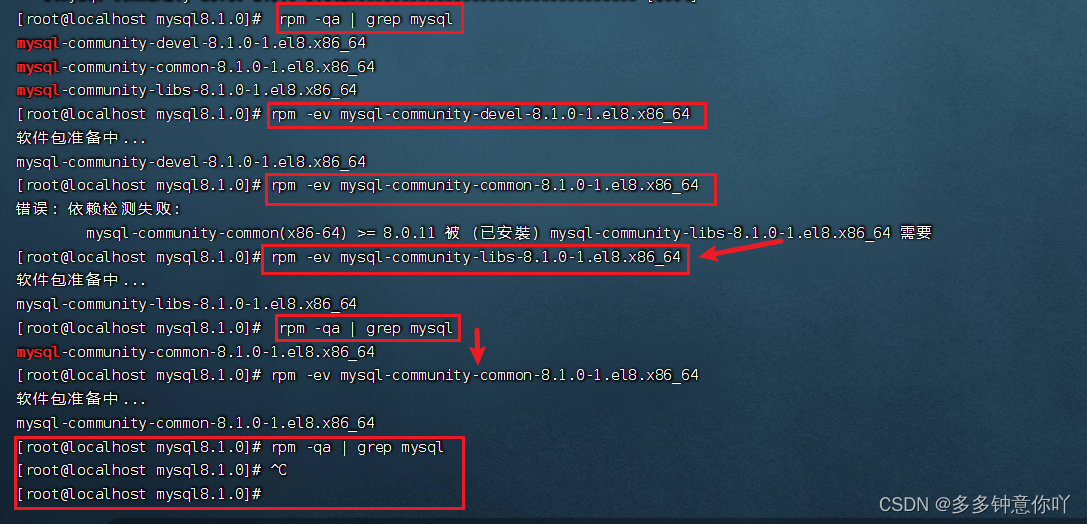
如何卸载在linux下通过rpm安装的mysql
目录 1.先关闭MySQL服务并查看运行状态 2.使用 rpm 管道命令的方式查看已安装的mysql 3. 使用rpm -ev 命令移除安装 4. 删除MySQL数据库内容 1.先关闭MySQL服务并查看运行状态 如果之前安装过并已经启动,则需要卸载前请先关闭MySQL服务 systemctl stop mysqld…...
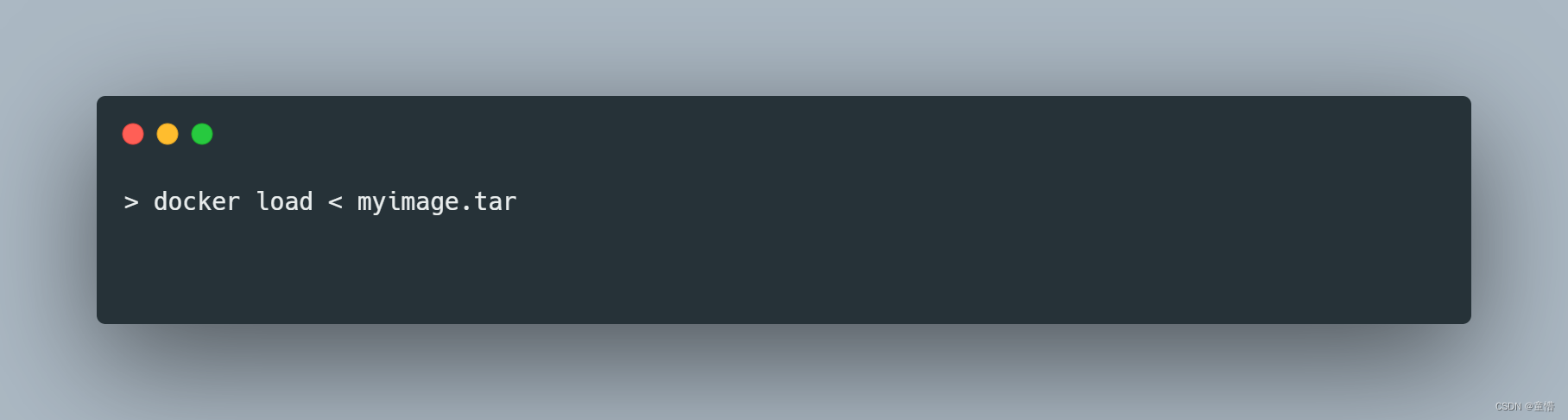
docker复制镜像文件
一、复制镜像 #1. 查找本机已有的镜像docker images |grep xxxx#2. 将镜像复制出来指向到xxxx.tar的文件中 docker save 343cca04e31d > xxxx.tareg: 二、加载镜像 直接将拷贝好的镜像包直接加载即可 docker load < myimage.tar...
自动驾驶学习笔记(六)——Apollo安装
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《2023星火培训【感知专项营】》免费课程—>传送门 文章目录 前言 Apollo安装 硬件配置 安装Ubuntu…...
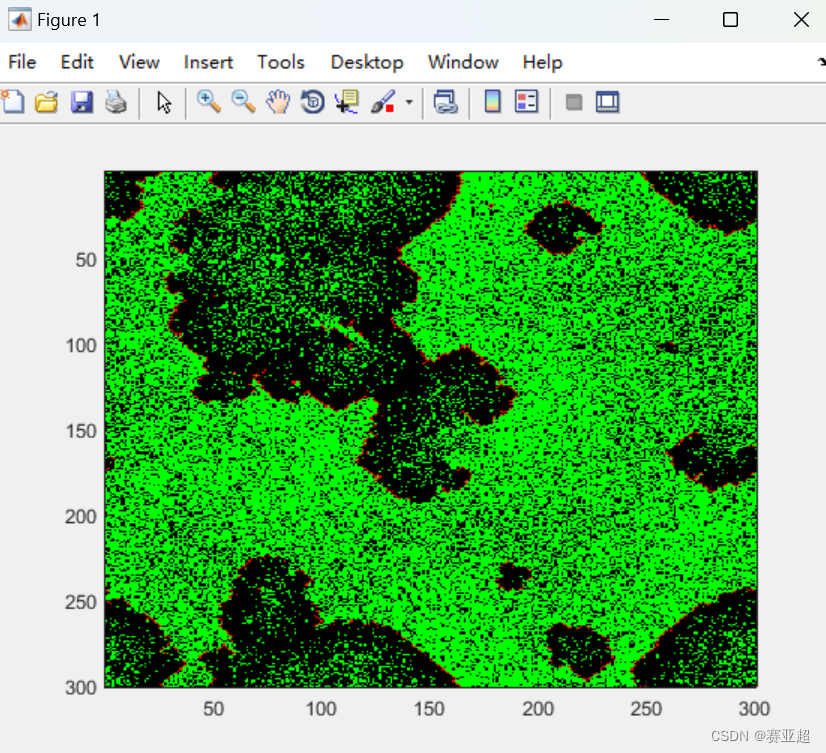
四阶龙格库塔与元胞自动机
龙格库塔法参考: 【精选】四阶龙格库塔算法及matlab代码_四阶龙格库塔法matlab_漫道长歌行的博客-CSDN博客 龙格库塔算法 Runge Kutta Method及其Matlab代码_龙格库塔法matlab_Lzh_023016的博客-CSDN博客 元胞自动机参考: 元胞自动机:森林…...

Mac安装opencvJava踩坑
SpringBoot导入opencv依赖 先将jar包添加到libraries中在resources目录下创建lib文件夹并复制jar包到这里添加如下依赖,并刷新maven <dependency><groupId>org.opencv</groupId><artifactId>opencv</artifactId><version>4.8.0…...

YOLOv8-Pose推理详解及部署实现
目录 前言一、YOLOv8-Pose推理(Python)1. YOLOv8-Pose预测2. YOLOv8-Pose预处理3. YOLOv8-Pose后处理4. YOLOv8-Pose推理 二、YOLOv8-Pose推理(C)1. ONNX导出2. YOLOv8-Pose预处理3. YOLOv8-Pose后处理4. YOLOv8-Pose推理 三、YOLOv8-Pose部署1. 源码下载2. 环境配置2.1 配置CM…...
django+drf+vue 简单系统搭建 (1) - django创建项目
本系列文章为了记录自己第一个系统生成过程,主要使用django,drf,vue。本人非专业人士,此文只为记录学习,若有部分描述不够准确的地方,烦请指正。 建立这个系统的原因是因为,在生活中,很多觉得可以一两行代码…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
