力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目:
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2]- 若旋转
7次,则可以得到[0,1,2,4,5,6,7]注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个元素值 互不相同 的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。来源:力扣(LeetCode)
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
示例:
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:输入:nums = [4,5,6,7,0,1,2]
输出:0解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:输入:nums = [11,13,15,17]
输出:11解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
解法:
使用min函数。
代码:
class Solution:def findMin(self, nums: List[int]) -> int:return min(nums)
相关文章:
)
力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目: 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转…...
matlab中实现画函数图像添加坐标轴
大家好,我是带我去滑雪! 主函数matlab代码: function PlotAxisAtOrigin(x,y); if nargin 2 plot(x,y);hold on; elsedisplay( Not 2D Data set !) end; Xget(gca,Xtick); Yget(gca,Ytick); XLget(gca,XtickLabel); YLget(gca,YtickLabel)…...
C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...
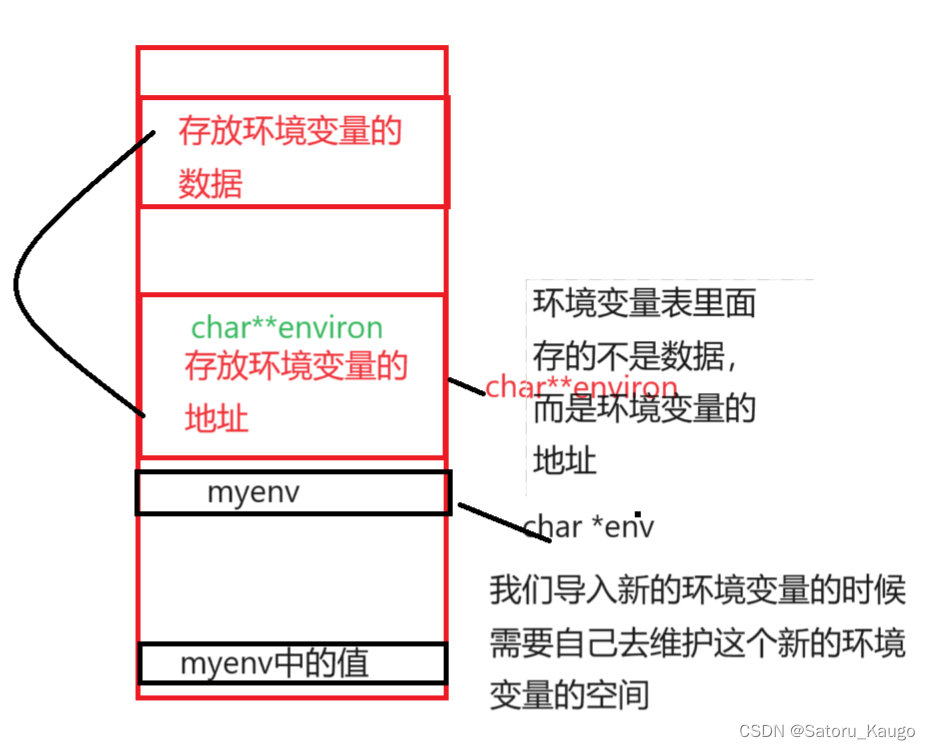
【Linux】Shell命令行的简易实现(C语言实现)内键命令,普通命令
文章目录 0.准备工作1.大体框架 一、获取命令行二、解析命令行三、进程执行1.普通命令2.内建命令 四、完整代码: 0.准备工作 1.大体框架 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <assert.h> #include <u…...
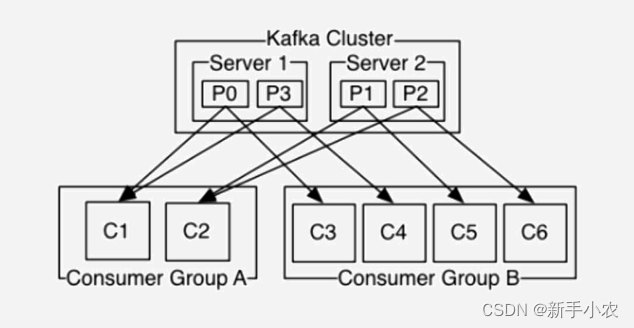
Kafka -- 架构、分区、副本
1、Kafka的架构: 1、producer:消息的生产者 2、consumer:消息的消费者 3、broker:kafka集群的服务者,一个broker就是一个节点,主要是负责处理消息的读、写的请求和存储消息。在kafka cluster中包含很多的br…...

CSS特效001:鼠标放div上,实现旋转、放大、移动等效果
GPT能够很好的应用到我们的代码开发中,能够提高开发速度。你可以利用其代码,做出一定的更改,然后实现效能。 css实战中,经常会看到这样的场景,鼠标放到一个图片或者一个div块状时候,会出现旋转、放大、移动…...

gin 快速入门手册
文章目录 安装URL和路由分组2. 带参数的url3. 获取路由分组的参数 获取参数1. 获取get参数2. 获取post参数3. get、post混合 JSON 、 ProtoBuf渲染1. 输出json和protobuf2. PureJSON 表单验证1. 表单的基本验证 中间件和next函数1. 无中间件启动2. 使用中间件3. 自定义组件 设置…...
Window下安装 Mongodb,并实现单点事务
在window操作系统下安装Mongodb,并让单点mongodb支持事务,mongodb5以上时才支持事务,所以必须时mongodb5及以上版本才支持。 1、下载mongodb安装文件 (1) 下载mongodb msi 安装文件 地址:mongocommunity &…...

【通信原理】第三章 随机过程——例题
一、随机过程 1. 数学特征 ① 随机信号(三角函数表达式) ② 随机信号(求和表达式) 2. 功率谱密度 ① 相位确定,求功率谱密度 ② 已知相位分布,求功率谱密度 ③ 信号为两信号之和,求功率谱密度…...
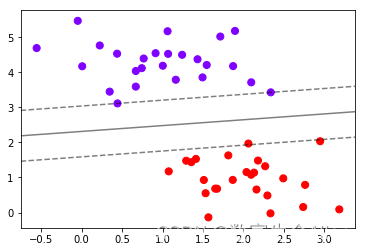
线性【SVM】数学原理和算法实现
一. 数学原理 SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。 如上图所…...

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
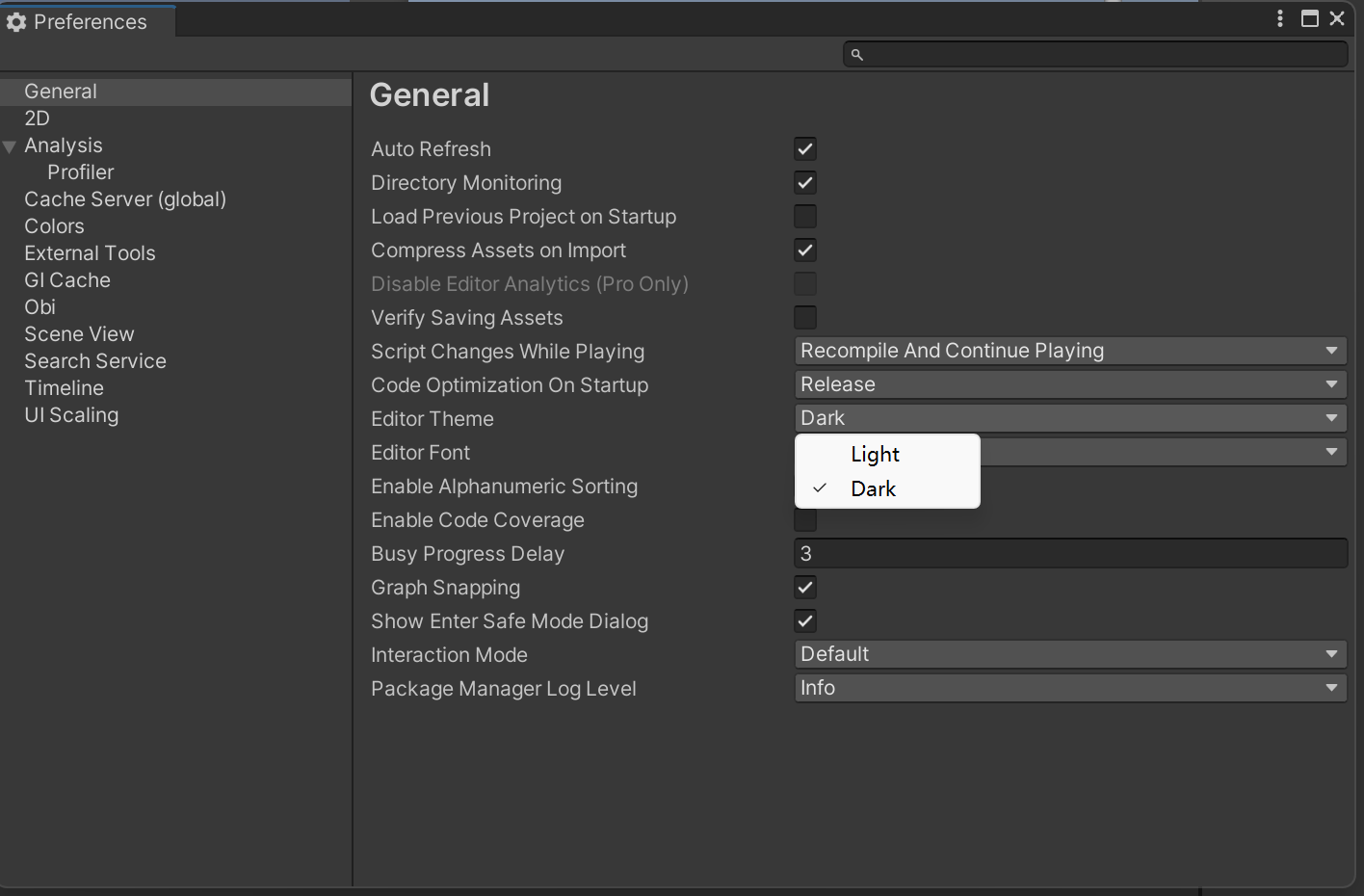
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...
解析找不到msvcr100.dll文件的解决方法,4个方法修复msvcr100.dll
msvcr100.dll是Microsoft Visual C 2010运行库的组成部分,一些基于Visual C开发的软件运行时会依赖这个dll文件。出现“找不到msvcr100.dll”的错误提示,往往意味着这个文件在你的计算机系统中丢失或损坏,导致相关程序无法正常运行。以下是找…...

达梦主备部署
达梦主备部署 一.概括1)环境软件下载2)集群规划 二.安装1)安装前2)安装数据库 三.主备机器部署1)初始化数据库(1)主库配置(2)备库配置 2)脱机备份(1)主服务器…...

后期混音效果全套插件Waves 14 Complete mac中文版新增功能
Waves 14 Complete for Mac是一款后期混音效果全套插件,Waves音频插件,内置混响,压缩,降噪和EQ等要素到建模的模拟硬件,环绕声和后期制作工具,包含全套音频效果器,是可以让你使用所有功能。Waves 14 Comple…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
