C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码:
/* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问
该数是多少?*/
#include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i = 10; i < 100; i++){//j*j为第二个完全平方数for (int j = i; j < 100; j++){//两个平方数相减为168if (j*j-i*i==168){num=i*i-100;printf("这个数为:%d",num);return 0;}}}
}运行截图:
相关文章:

C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...
【Linux】Shell命令行的简易实现(C语言实现)内键命令,普通命令
文章目录 0.准备工作1.大体框架 一、获取命令行二、解析命令行三、进程执行1.普通命令2.内建命令 四、完整代码: 0.准备工作 1.大体框架 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <assert.h> #include <u…...
Kafka -- 架构、分区、副本
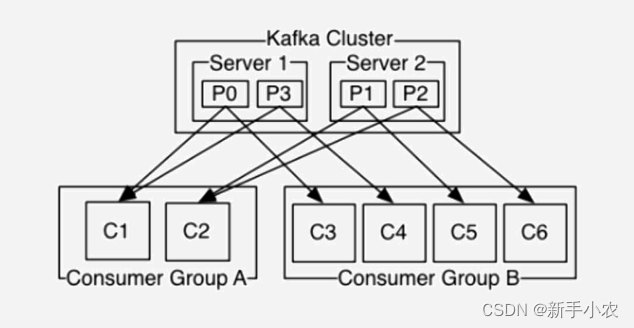
1、Kafka的架构: 1、producer:消息的生产者 2、consumer:消息的消费者 3、broker:kafka集群的服务者,一个broker就是一个节点,主要是负责处理消息的读、写的请求和存储消息。在kafka cluster中包含很多的br…...

CSS特效001:鼠标放div上,实现旋转、放大、移动等效果
GPT能够很好的应用到我们的代码开发中,能够提高开发速度。你可以利用其代码,做出一定的更改,然后实现效能。 css实战中,经常会看到这样的场景,鼠标放到一个图片或者一个div块状时候,会出现旋转、放大、移动…...

gin 快速入门手册
文章目录 安装URL和路由分组2. 带参数的url3. 获取路由分组的参数 获取参数1. 获取get参数2. 获取post参数3. get、post混合 JSON 、 ProtoBuf渲染1. 输出json和protobuf2. PureJSON 表单验证1. 表单的基本验证 中间件和next函数1. 无中间件启动2. 使用中间件3. 自定义组件 设置…...
Window下安装 Mongodb,并实现单点事务
在window操作系统下安装Mongodb,并让单点mongodb支持事务,mongodb5以上时才支持事务,所以必须时mongodb5及以上版本才支持。 1、下载mongodb安装文件 (1) 下载mongodb msi 安装文件 地址:mongocommunity &…...

【通信原理】第三章 随机过程——例题
一、随机过程 1. 数学特征 ① 随机信号(三角函数表达式) ② 随机信号(求和表达式) 2. 功率谱密度 ① 相位确定,求功率谱密度 ② 已知相位分布,求功率谱密度 ③ 信号为两信号之和,求功率谱密度…...
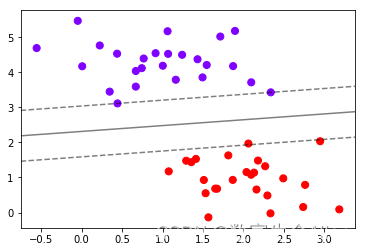
线性【SVM】数学原理和算法实现
一. 数学原理 SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。 如上图所…...

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
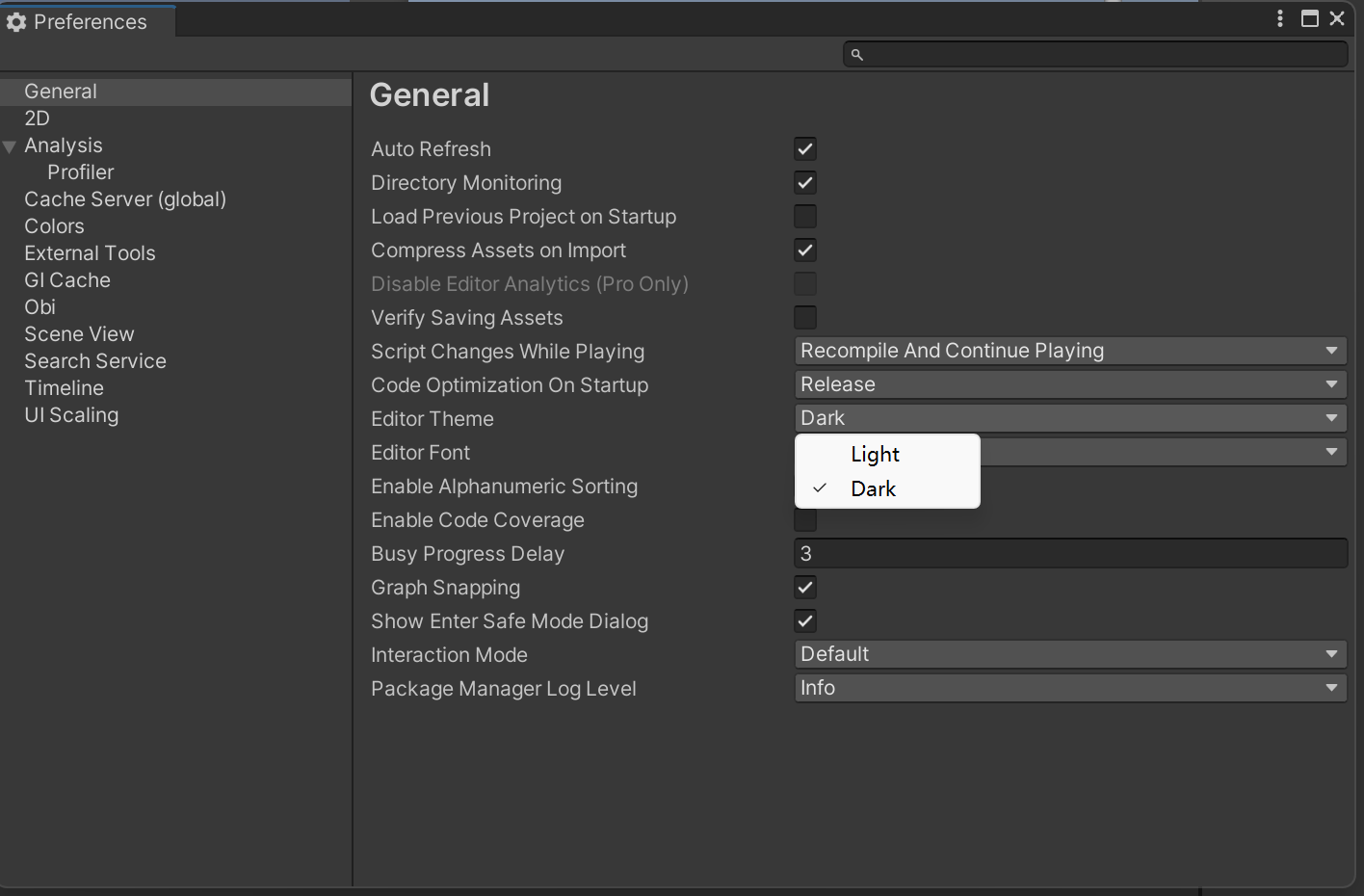
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
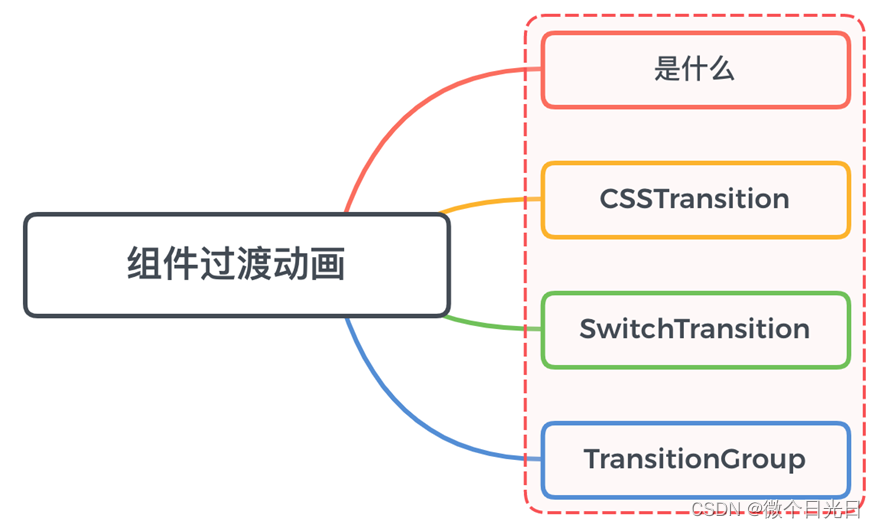
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...
解析找不到msvcr100.dll文件的解决方法,4个方法修复msvcr100.dll
msvcr100.dll是Microsoft Visual C 2010运行库的组成部分,一些基于Visual C开发的软件运行时会依赖这个dll文件。出现“找不到msvcr100.dll”的错误提示,往往意味着这个文件在你的计算机系统中丢失或损坏,导致相关程序无法正常运行。以下是找…...

达梦主备部署
达梦主备部署 一.概括1)环境软件下载2)集群规划 二.安装1)安装前2)安装数据库 三.主备机器部署1)初始化数据库(1)主库配置(2)备库配置 2)脱机备份(1)主服务器…...

后期混音效果全套插件Waves 14 Complete mac中文版新增功能
Waves 14 Complete for Mac是一款后期混音效果全套插件,Waves音频插件,内置混响,压缩,降噪和EQ等要素到建模的模拟硬件,环绕声和后期制作工具,包含全套音频效果器,是可以让你使用所有功能。Waves 14 Comple…...

HTML5笔记
前端学习笔记专栏区别于官网中全面的知识讲解,主要记录学习技术栈时对于重点内容的提炼,便于对技术栈知识的快速回顾以及使用 1.canvas元素 内部坐标:坐标均以左上角为(0, 0),单一坐标均作为起始坐标创建对象: <c…...

前端架构师需要解决那些问题
假设你是一个大型后台管理系统的前端架构师,你需要解决那些问题? 1、Ui设计规范 大型系统UI得统一吧?各个业务模块的UI设计得高效吧?那就得有规范,直观的说就是原子设计那套东西。加一堆推荐设计稿。 2、基础组件库…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
