线性【SVM】数学原理和算法实现
一. 数学原理
SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。

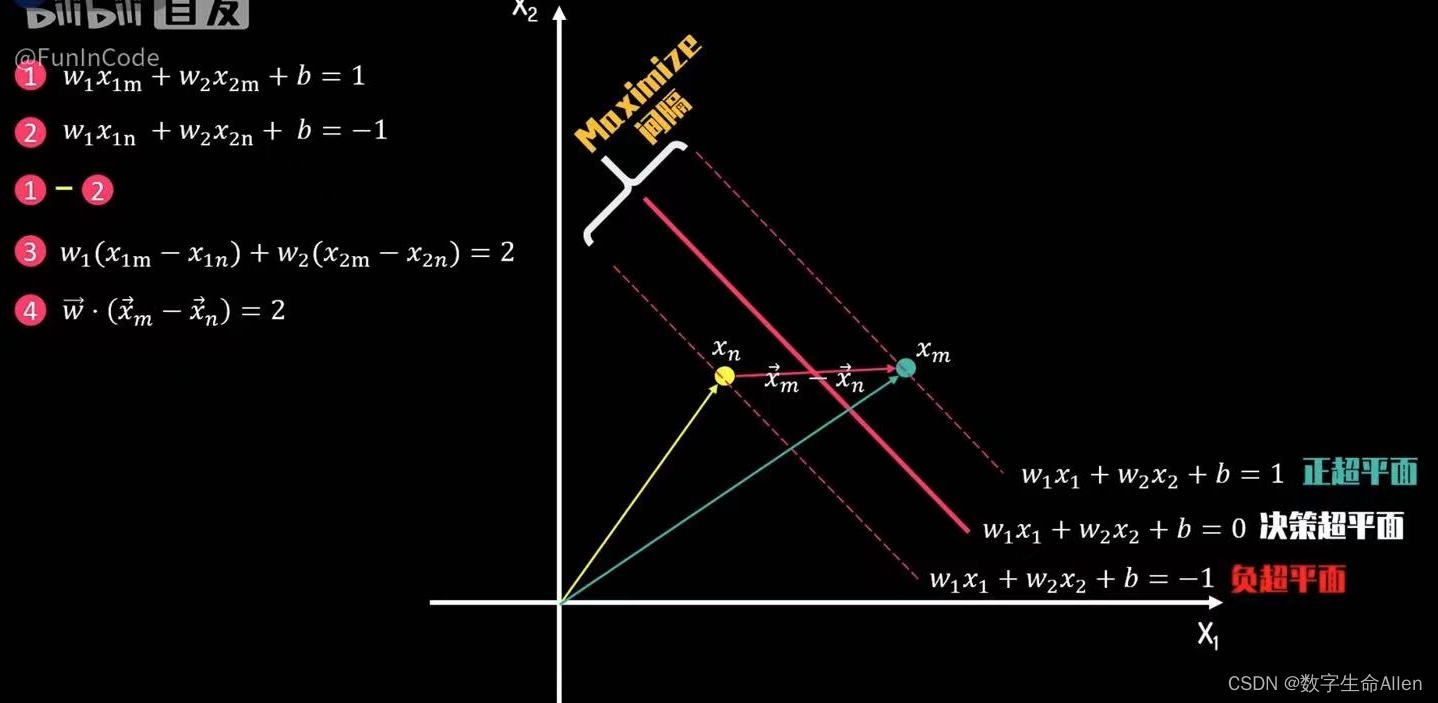
如上图所示,正超平面,负超平面和决策超平面的表达式如图所示,假设现在在正负超平面上有Xm和Xn两个支持向量,表达式分别是①,②,①减②得到③,③可以写成④的形式(其中,w向量 = (w1,w2),Xm向量 = (X1m,X2m),Xn向量 = (X1n,X2n))。
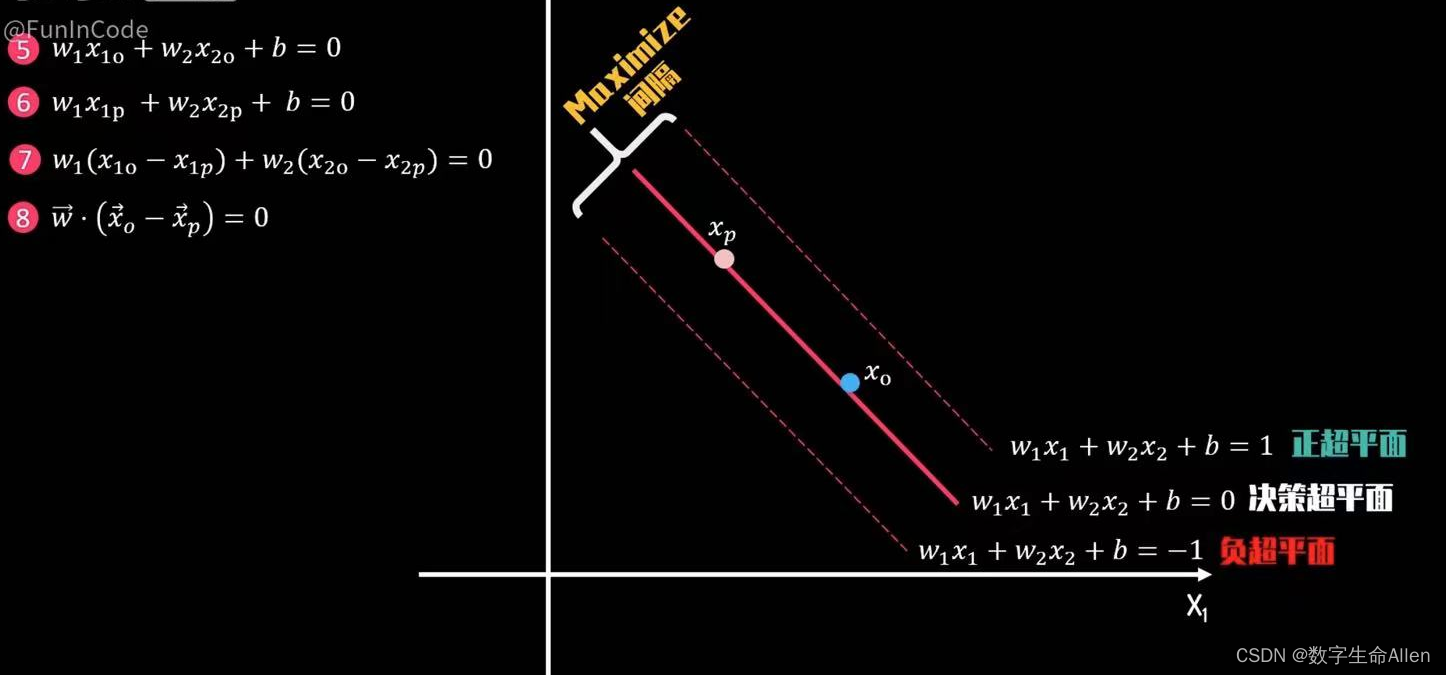
选择假设决策超平面上有Xp = (X1p,X2p)和Xo(X1o,X2o)两个向量,那么可以得到⑤和⑥,⑤-⑥ = ⑦,⑦可以写成⑧的形式。因此w向量是一个垂直于决策超平面的向量,即决策超平面的法向量。
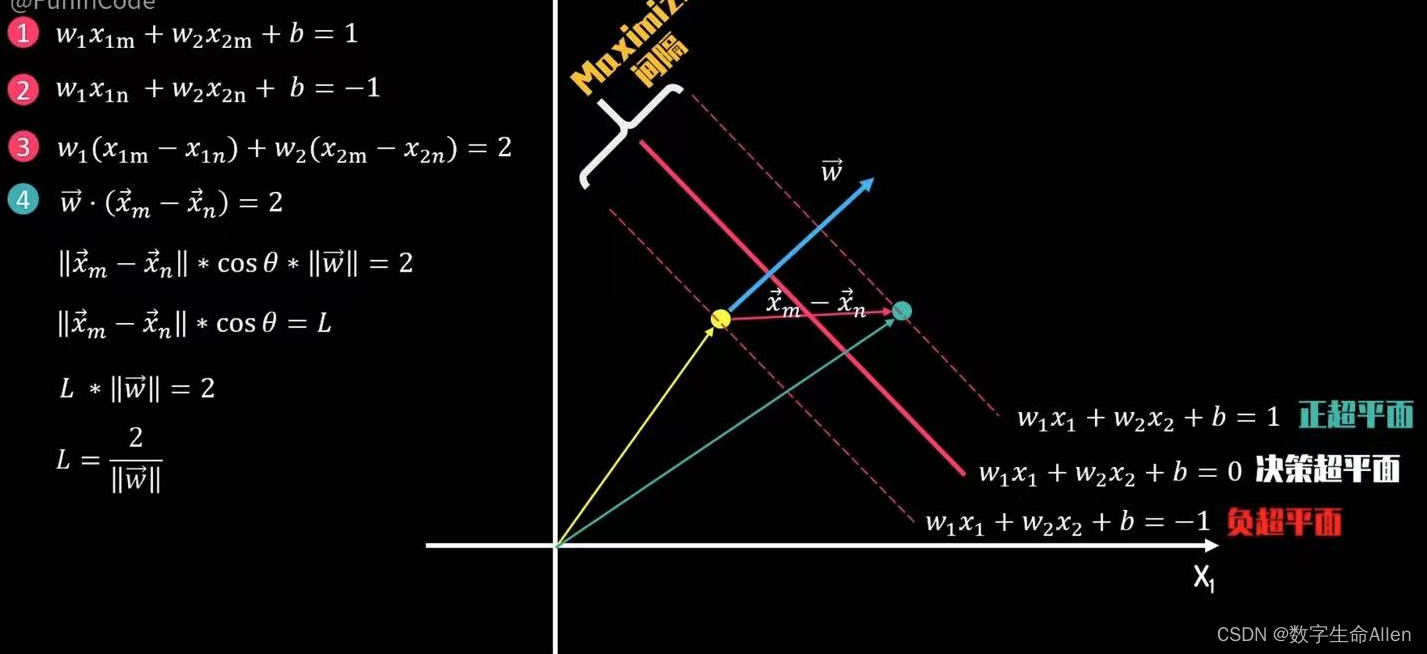
现在我们再回到④式,可以知道正负超平面之间的距离d可以表示为:d = 2/w的范数。
现在我们再来看约束条件,所有正超平面上方的点yi = 1,所有负超平面下方的点yi = -1,因此约束表达式可以写成:

所以这个优化问题就转变为一个典型的凸优化问题:
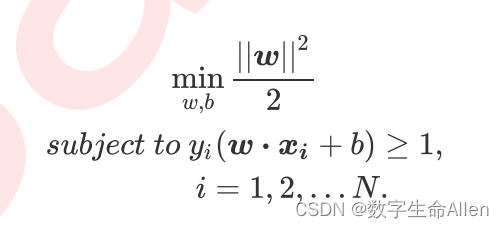
首先我们使用拉格朗日乘数来将损失函数改写成考虑了约束条件的形式:
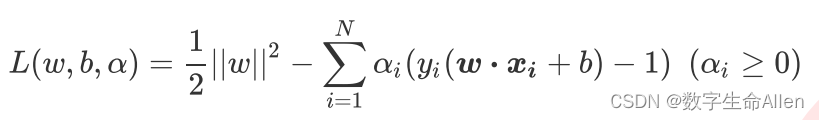
上述式子被称为拉格朗日函数,其中αi就叫做拉格朗日乘数。此时此刻,我们要求解的就不只有参数向量和截距,我们也要求解拉格朗日乘数 ,而我们的Xi和Yi都是我们已知的特征矩阵和标签。对上面的式子分别对w和b求偏导,可以得到下述的结论:

在这里我们引入拉格朗日对偶函数。对于任何一个拉格朗日函数 L(x,α),都存在一个与它对应的对偶函数g(α) ,只带有拉格朗日乘数作为唯一的参数。如果L(x,α)的最优解存在并可以表示为 min L(x,α),并且对偶函数的最优解也存在 并可以表示为max g(α) ,则我们可以定义对偶差异,即拉格朗日函数的最优解与其对偶函数的最优解之间的差值:
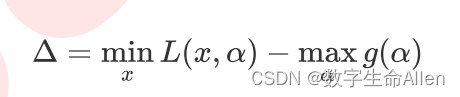
如果 △ = 0,则称L(x,α)与其对偶函数之间存在强对偶关系,此时我们就可以通过求解其对偶函数的最优解来替代求解原始函数的最优解。在这里我们可以通过求对偶函数的最大值得到原函数的最小值。强对偶关系要想存在,必须满足KKT条件:

一旦KKT条件被满足,我们就可以通过求对偶函数的最大值来求出α的值。求出α后我们就可以通过结合上述的表达式求解出w和b,进而得到了决策边界的表达式。得到了决策边界的表达式就可以利用决策边界和其有关的超平面来分类了。
二. 算法实现
我们先来导入相应的模块:
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np使用make_blot函数绘制出散点图的坐标,并用plt.scatter绘制:
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")#rainbow彩虹色
plt.xticks([])
plt.yticks([])
plt.show()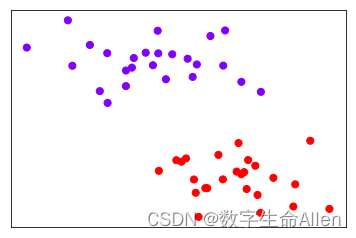
创建一个子图对象,以便后续操作:
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图为了绘制决策超平面,我们通过下面的代码块绘制网格点:
#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()
ylim = ax.get_ylim()#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)axisy,axisx = np.meshgrid(axisy,axisx)
#我们将使用这里形成的二维数组作为我们contour函数中的X和Y
#使用meshgrid函数将两个一维向量转换为特征矩阵
#核心是将两个特征向量广播,以便获取y.shape * x.shape这么多个坐标点的横坐标和纵坐标xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#其中ravel()是降维函数,vstack能够将多个结构一致的一维数组按行堆叠起来
#xy就是已经形成的网格,它是遍布在整个画布上的密集的点plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")#理解函数meshgrid和vstack的作用
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)v1,v2 = np.meshgrid(a,b)v1v2v = np.vstack([v1.ravel(), v2.ravel()]).T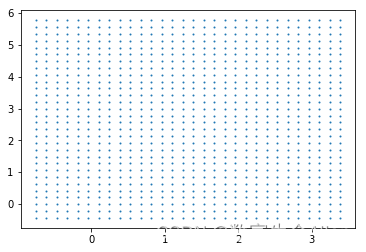
接下来通过下面的代码块绘制出决策边界:
#建模,通过fit计算出对应的决策边界
clf = SVC(kernel = "linear").fit(X,y)#计算出对应的决策边界
Z = clf.decision_function(xy).reshape(axisx.shape)
#重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离
#然后再将这个距离转换为axisx的结构,这是由于画图的函数contour要求Z的结构必须与X和Y保持一致#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
#画决策边界和平行于决策边界的超平面
ax.contour(axisx,axisy,Z,colors="k",levels=[-1,0,1] #画三条等高线,分别是Z为-1,Z为0和Z为1的三条线,alpha=0.5#透明度,linestyles=["--","-","--"])ax.set_xlim(xlim)#设置x轴取值
ax.set_ylim(ylim)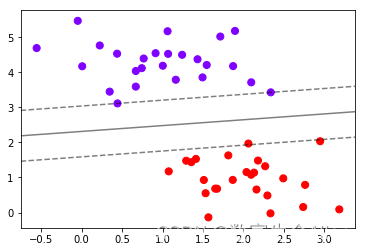
可以看到决策边界和正负超平面已经被绘制出来了。
我们可以将上述过程打包成函数:
#将上述过程包装成函数:
def plot_svc_decision_function(model,ax=None):if ax is None:ax = plt.gca()xlim = ax.get_xlim()ylim = ax.get_ylim()x = np.linspace(xlim[0],xlim[1],30)y = np.linspace(ylim[0],ylim[1],30)Y,X = np.meshgrid(y,x) xy = np.vstack([X.ravel(), Y.ravel()]).TP = model.decision_function(xy).reshape(X.shape)ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"]) ax.set_xlim(xlim)ax.set_ylim(ylim)#则整个绘图过程可以写作:
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow") # 画散点图
clf = SVC(kernel = "linear").fit(X,y) # 计算决策边界
plot_svc_decision_function(clf) # 画出决策边界下面是clf的一些属性:
clf.predict(X)
#根据决策边界,对X中的样本进行分类,返回的结构为n_samplesclf.score(X,y)
#返回给定测试数据和标签的平均准确度clf.support_vectors_
#返回支持向量坐标clf.n_support_#array([2, 1])
#返回每个类中支持向量的个数相关文章:

线性【SVM】数学原理和算法实现
一. 数学原理 SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。 如上图所…...

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
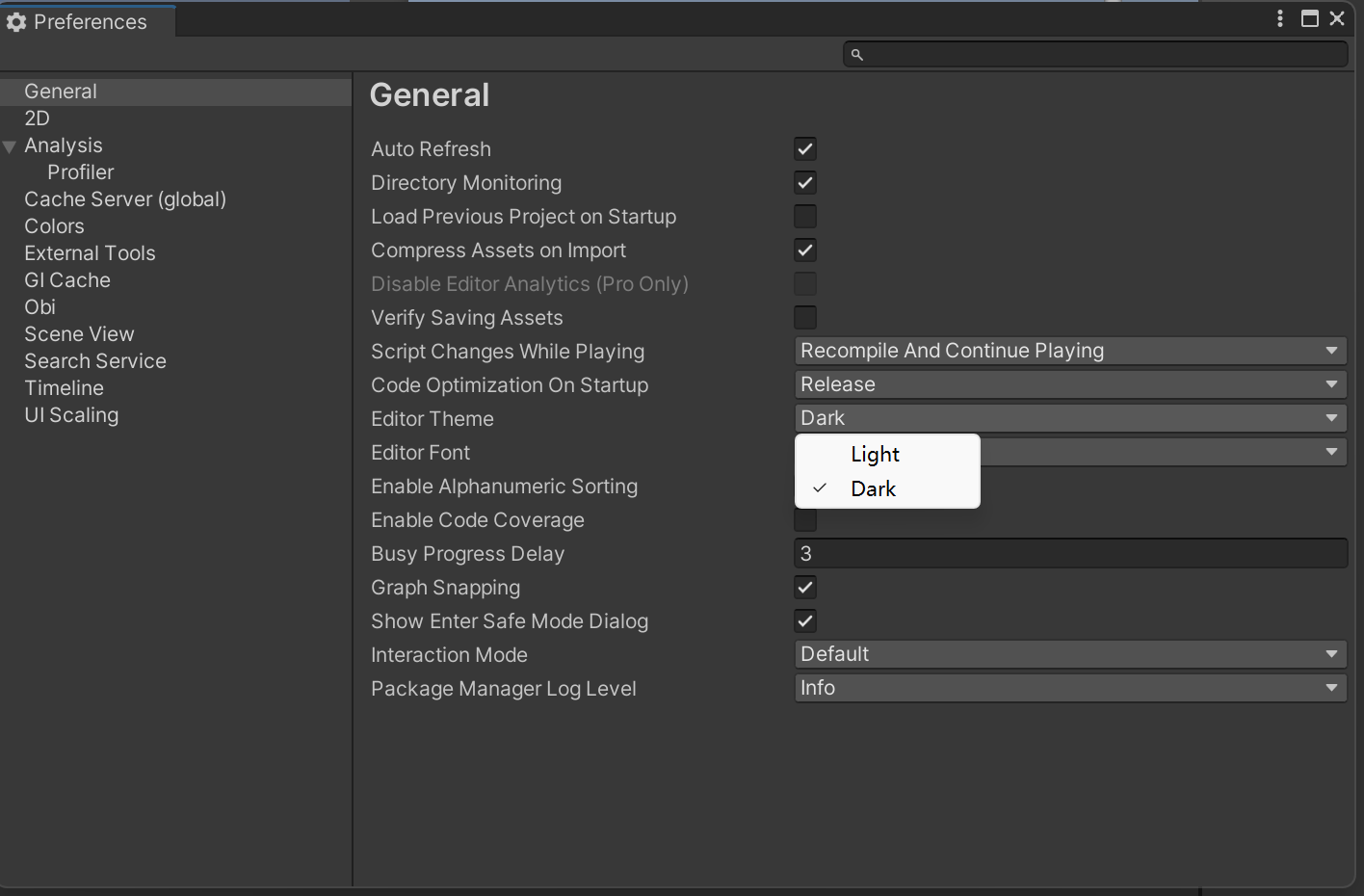
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
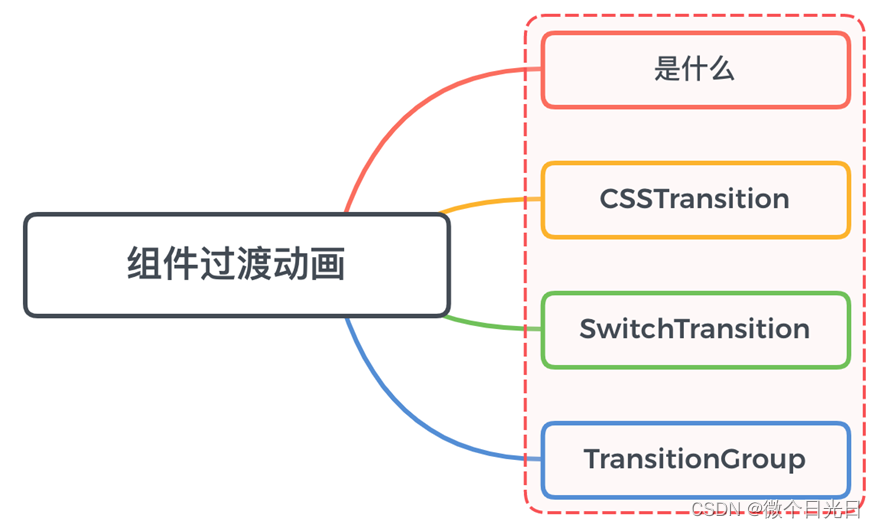
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...
解析找不到msvcr100.dll文件的解决方法,4个方法修复msvcr100.dll
msvcr100.dll是Microsoft Visual C 2010运行库的组成部分,一些基于Visual C开发的软件运行时会依赖这个dll文件。出现“找不到msvcr100.dll”的错误提示,往往意味着这个文件在你的计算机系统中丢失或损坏,导致相关程序无法正常运行。以下是找…...

达梦主备部署
达梦主备部署 一.概括1)环境软件下载2)集群规划 二.安装1)安装前2)安装数据库 三.主备机器部署1)初始化数据库(1)主库配置(2)备库配置 2)脱机备份(1)主服务器…...

后期混音效果全套插件Waves 14 Complete mac中文版新增功能
Waves 14 Complete for Mac是一款后期混音效果全套插件,Waves音频插件,内置混响,压缩,降噪和EQ等要素到建模的模拟硬件,环绕声和后期制作工具,包含全套音频效果器,是可以让你使用所有功能。Waves 14 Comple…...

HTML5笔记
前端学习笔记专栏区别于官网中全面的知识讲解,主要记录学习技术栈时对于重点内容的提炼,便于对技术栈知识的快速回顾以及使用 1.canvas元素 内部坐标:坐标均以左上角为(0, 0),单一坐标均作为起始坐标创建对象: <c…...

前端架构师需要解决那些问题
假设你是一个大型后台管理系统的前端架构师,你需要解决那些问题? 1、Ui设计规范 大型系统UI得统一吧?各个业务模块的UI设计得高效吧?那就得有规范,直观的说就是原子设计那套东西。加一堆推荐设计稿。 2、基础组件库…...

使用python快速搭建接口自动化测试脚本实战总结
导读 本文将介绍如何使用python快速进行http/https接口自动化测试脚本搭建,实现自动请求、获取结果、数据对比分析,导出结果到Excel等功能,包括python的requests、pandas、openpyxl等库的基本使用方法。 测试需求介绍 通常,在我…...
android studio 字节码查看工具jclasslib bytecode viewer
jclasslib bytecode viewer 是一款非常好用的.class文件查看工具; jclasslib bytecode editor is a tool that visualizes all aspects of compiled Java class files and the contained bytecode. Many aspects of class files can be edited in the UI. In addit…...

Ubuntu上搭建FTP服务
要在Ubuntu上搭建FTP服务器,可以使用常见的FTP服务器软件如vsftpd(Very Secure FTP Daemon)或ProFTPD。以下是使用vsftpd在Ubuntu上设置FTP服务器的基本步骤: 步骤 1: 安装 vsftpd 打开终端并运行以下命令安装 vsftpd:…...
unity打AB包,AssetBundle预制体与图集(三)
警告: spriteatlasmanager.atlasrequested wasn’t listened to while 条件一:图片打图集里面去了 条件二:然后图集打成AB包了 条件三:UI预制体也打到AB包里面去了 步骤一:先加载了图集 步骤二:再加载UI预…...

在Javascript中为什么 0.1+0.2 不等于0.3 ? 源代码详细解析
在JavaScript中,浮点数计算可能会导致精度问题,这就是为什么0.1 0.2不等于0.3的原因。这是因为JavaScript使用IEEE 754标准来表示浮点数,而该标准使用二进制来表示小数。 让我们通过一个实例来详细解释这个问题。考虑以下代码: …...

MATLAB|热力日历图
目录 日历图介绍: 热力日历图的特点: 应用场景: 绘图工具箱 属性 (Properties) 构造函数 (Constructor) 公共方法 (Methods) 私有方法 (Private Methods) 使用方法 日历图介绍: 热力日历图是一种数据可视化形式…...
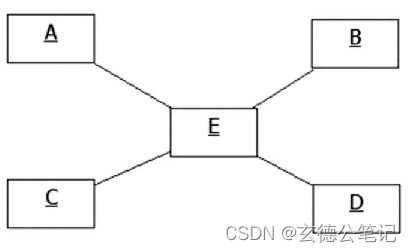
《golang设计模式》第三部分·行为型模式-05-仲裁者/中介模式(Mediator)
文章目录 1. 概述1.1 作用1.2 角色1.3 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 仲裁者(Mediator)可以封装和协调多个对象之间的耦合交互行为,以减弱这些对象之间的耦合关联。 1.1 作用 将多个对象相互耦合的设计转变为所有对象…...
7天入门python系列之准备工作
寄语 编者打算开一个python 初学主题的系列文章,用于指导想要学习python的同学。关于文章有任何疑问都可以私信作者。对于初学者想在7天内入门Python,这是一个紧凑的学习计划。但并不是不可完成的。 7天的安排 如果你想在7天内入门Python,…...

Go语言~反射
reflect包 type name和type kindValueOf通过反射获取值通过反射设置变量的值 package mainimport ("fmt""reflect" )func reflectType(x interface{}) {obj : reflect.TypeOf(x)fmt.Println(obj, obj.Name(), obj.Kind())fmt.Printf("obj type of %…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
