AM@向量代数@向量基本概念和向量线性运算
文章目录
- abstract
- 向量的基本概念
- 向量
- 向量的坐标分解式和坐标👺
- 向量的模@向量的长度(大小)👺
- 零向量
- 单位向量👺
- 方向向量
- 非零向量的单位向量@正规化
- 向量夹角👺
- 向量方向角和向量间夹角@投影
- 几何描述向量的线性运算
- 向量的加减运算
- 向量的三角形三边不等式
- 数乘
- 方程的思想求解向量相关问题
- 向量的线性运算的坐标表示公式
abstract
- 向量代数@向量基本概念和向量线性运算
向量的基本概念
- 平面向量和空间向量是类似的,这里主要以空间向量为主讨论
向量
- 既有大小(模)又有方向的量,称为向量(或矢量)
- 印刷体常用黑体字母表示向量
- 手写通常用头箭头表示向量
- 向量的大小也被称为模
- 只考虑方向和大小(而不考虑起点)的向量称为自由向量
- 这里的向量是抽象向量的一个简化版本 n n n个数构成的数组,而在例如高等代数中讨论的,在线性空间中有含义更加广的向量以及更加深刻的性质研究
向量的坐标分解式和坐标👺
- 向量的坐标(表示):
- 向量的终点在坐标轴上的投影坐标 a x , a y , a z a_x,a_y,a_z ax,ay,az叫做向量 a \boldsymbol{a} a的坐标,记为 a = ( a x , a y , a z ) \boldsymbol{a}=(a_x,a_y,a_z) a=(ax,ay,az)
- 向量的坐标分解式= a x i + a y j + a z k a_{x}\boldsymbol{i}+a_{y}\boldsymbol{j}+a_{z}\boldsymbol{k} axi+ayj+azk
- 更多详见向量坐标分解式相关章节
向量的模@向量的长度(大小)👺
- 向量的模: a T = ( a x , a y , a z ) \boldsymbol{a}^T=(a_x,a_y,a_z) aT=(ax,ay,az),则 ∣ a ∣ = a x 2 + a y 2 + a z 2 |\boldsymbol{a}|=\sqrt{a_x^2+a_y^2+a_z^2} ∣a∣=ax2+ay2+az2= ( a x , a y , z y ) ⋅ ( a x , a y , a z ) \sqrt{(a_x,a_y,z_y)\cdot(a_x,a_y,a_z)} (ax,ay,zy)⋅(ax,ay,az)
- 在空间直角坐标系中,该公式是根据勾股定理得到
- a ⋅ a = a x 2 + a y 2 + a z 2 \boldsymbol{a}\cdot\boldsymbol{a}=a_x^2+a_y^2+a_z^2 a⋅a=ax2+ay2+az2,这里假设 a \boldsymbol{a} a是列向量
- 如果引入矩阵乘法(向量内积)的表示方法,还可以写作 ∣ a ∣ = a T a |\boldsymbol{a}|=\sqrt{\boldsymbol{a}^T\boldsymbol{a}} ∣a∣=aTa,其中 a T , a \bold{a}^T,\bold{a} aT,a分别是行向量以及其转置得到的列向量
零向量
- 零向量:模为0的向量称为零向量,其方向可以看作任意的,记为 0 \bold{0} 0或 0 ⃗ \vec{0} 0
- 由于零向量与另一个向量的夹角的取值在 [ 0 , π ] [0,\pi] [0,π]内任意取值,因此可以认为零向量和任意向量平行,也可以认为零向量和任意向量垂直
单位向量👺
- 单位向量:模为1的向量称为单位向量
- 通常向量 a \boldsymbol{a} a的同向单位向量记为 a 0 \boldsymbol{a}^{0} a0
- 对于给定的一个方向 l \boldsymbol{l} l,记该方向的单位向量为 e l \boldsymbol{e}_{\boldsymbol{l}} el或 l 0 \boldsymbol{l}_0 l0或 l 0 \boldsymbol{l}^{0} l0,或 u \mathbf{u} u
- 每个方向都有单位向量,方向相同的向量的单位向量完全相同
- 不同方向的单位向量长度都为1,但是方向不同
- 向量的坐标和单位向量表示加法表示
- 取 i = ( 1 , 0 , 0 ) \boldsymbol i=(1,0,0) i=(1,0,0), j = ( 0 , 1 , 0 ) \boldsymbol j=(0,1,0) j=(0,1,0), k = ( 0 , 0 , 1 ) \boldsymbol k=(0,0,1) k=(0,0,1),它们分别是 x , y , z x,y,z x,y,z轴的方向单位向量
- 则 a = ( a x , a y , a z ) = a x i + a y j + a z k \boldsymbol{a}=(a_x,a_y,a_z)=a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k} a=(ax,ay,az)=axi+ayj+azk
方向向量
- 这个概念在讨论解析几何中的直线时,直线的点向式方程由直线的某个方向向量和直线上的一个点确定
- 方向向量不一定是单位向量
- 例如,直线 l l l过 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0),直线的某个方向向量为 ( 1 , 2 ) (1,2) (1,2),则方程可以表示为 x − x 0 1 \frac{x-x_0}{1} 1x−x0= y − y 0 1 \frac{y-y_0}{1} 1y−y0
非零向量的单位向量@正规化
-
设非零向量 a = ( a x , a y , a z ) a=(a_x,a_y,a_z) a=(ax,ay,az)
- a 0 = a ∣ a ∣ a^{0}=\frac{a}{|a|} a0=∣a∣a= 1 ∣ a ∣ ( a x , a y , a z ) \frac{1}{|a|}(a_x,a_y,a_z) ∣a∣1(ax,ay,az)
-
使用范数表示
-
∣ ∣ a ∣ ∣ ||a|| ∣∣a∣∣表示向量 a a a的 L 2 L^2 L2范数
-
β = 1 ∣ ∣ α ∣ ∣ α \beta=\frac{1}{||\alpha||}\alpha β=∣∣α∣∣1α的长度一定是1
-
∣ ∣ β ∣ ∣ ||\beta|| ∣∣β∣∣= ∣ ∣ 1 ∣ ∣ α ∣ ∣ α ∣ ∣ \left|\left|\frac{1}{||\alpha||}\alpha\right|\right| ∣∣α∣∣1α = 1 ∣ ∣ α ∣ ∣ ∣ ∣ α ∣ ∣ = 1 \frac{1}{||\alpha||}||\alpha||=1 ∣∣α∣∣1∣∣α∣∣=1
-
向量夹角👺
- 向量夹角
- 设向量 a = O A → , b = O B → a=\overrightarrow{OA},b=\overrightarrow{OB} a=OA,b=OB,则他们的夹角记为 θ = ∠ A O B = < a , b > , 且 θ ∈ [ 0 , π ] \theta=\angle{AOB}=<a,b>,且\theta\in[0,\pi] θ=∠AOB=<a,b>,且θ∈[0,π]
- 若 θ = 0 \theta=0 θ=0,则 a , b a,b a,b同向
- 若 θ = π \theta=\pi θ=π,则 a , b a,b a,b反向
- 两者统称为 a , b a,b a,b平行,记为 a ∥ b a\parallel{b} a∥b
- 若 a = λ b a=\lambda{b} a=λb,则 a , b a,b a,b平行
- 若 λ > 0 \lambda>0 λ>0, a , b a,b a,b同向
- 若 λ < 0 \lambda<0 λ<0, a , b a,b a,b反向
- 若 θ = π 2 \theta=\frac{\pi}{2} θ=2π,则 a ⊥ b a\perp{b} a⊥b
- 设向量 a = O A → , b = O B → a=\overrightarrow{OA},b=\overrightarrow{OB} a=OA,b=OB,则他们的夹角记为 θ = ∠ A O B = < a , b > , 且 θ ∈ [ 0 , π ] \theta=\angle{AOB}=<a,b>,且\theta\in[0,\pi] θ=∠AOB=<a,b>,且θ∈[0,π]
向量方向角和向量间夹角@投影
- 另见向量的方向角和方向余弦@向量间夹角余弦@投影和向量分量
几何描述向量的线性运算
- 平面二维向量和空间三维向量的运算类似
向量的加减运算
-
借助平行四边形或三角形法则,从几何的角度描述向量的加法和减法
-
并且减法可以转换为加法 a − b = a + ( − b ) \boldsymbol{a}-\boldsymbol{b}=\boldsymbol{a}+(-\boldsymbol{b}) a−b=a+(−b)
-
向量加减运算的代数(坐标)运算比较简单,只需要将向量对应分量相加减: a ± b \boldsymbol{a}\pm\boldsymbol{b} a±b= ( a x ± b x , a y ± b y , a z ± b z ) (a_{x}\pm{b_x},a_y\pm{b_y},a_{z}\pm{b_z}) (ax±bx,ay±by,az±bz)
-
向量加法满足交换律和结合律
-
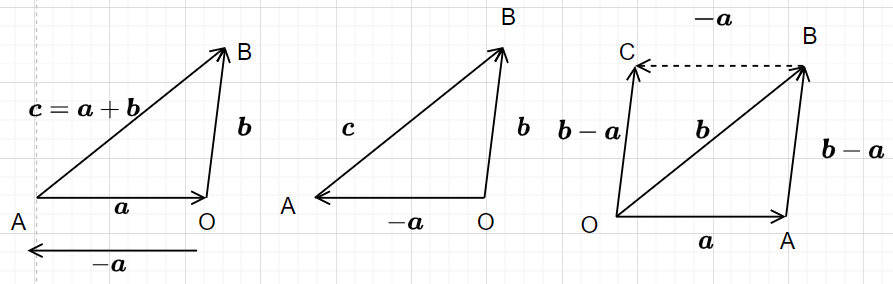
- c = A B → \boldsymbol{c}=\overrightarrow{AB} c=AB=$\overrightarrow{AO}+\overrightarrow{OB}
= = =\overrightarrow{OB}-\overrightarrow{OA}$ - 并且 ∣ a − b ∣ = ∣ b − a ∣ |\boldsymbol{a}-\boldsymbol{b}|=|\boldsymbol{b}-\boldsymbol{a}| ∣a−b∣=∣b−a∣
- c = A B → \boldsymbol{c}=\overrightarrow{AB} c=AB=$\overrightarrow{AO}+\overrightarrow{OB}
向量的三角形三边不等式
-
由三角形两边之和大于第三边,对应向量三角形法则下的向量加法和向量减法满足不等式:
-
∣ a + b ∣ ⩽ ∣ a ∣ + ∣ b ∣ |\boldsymbol{a}+\boldsymbol{b}|\leqslant{|\boldsymbol{a}|+|\boldsymbol{b}|} ∣a+b∣⩽∣a∣+∣b∣
-
∣ a − b ∣ |\boldsymbol{a}-\boldsymbol{b}| ∣a−b∣= ∣ b − a ∣ ⩽ ∣ a ∣ + ∣ b ∣ |\boldsymbol{b}-\boldsymbol{a}| \leqslant{|\boldsymbol{a}|+|\boldsymbol{b}|} ∣b−a∣⩽∣a∣+∣b∣
-
-
等号在 a , b \bold{a,b} a,b同向或反向时成立
数乘
-
设 λ \lambda λ是一个数, λ α \lambda{\boldsymbol{\alpha}} λα是一个向量, ∣ λ α ∣ = ∣ λ ∣ ∣ α ∣ |\lambda{\boldsymbol\alpha}|=|\lambda||\boldsymbol\alpha| ∣λα∣=∣λ∣∣α∣
- 当 λ > 0 \lambda>0 λ>0, λ α \lambda\boldsymbol{\alpha} λα与 α \boldsymbol{\alpha} α同向
- 当 λ = 0 \lambda=0 λ=0, λ α = 0 \lambda\boldsymbol{\alpha}=\boldsymbol{0} λα=0
- 当 λ < 0 \lambda<0 λ<0, λ α \lambda\boldsymbol{\alpha} λα和 α \boldsymbol{\alpha} α反向
-
代数表示:设 α = ( a x , a y , a z ) \boldsymbol{\alpha}=(a_{x},a_y,a_z) α=(ax,ay,az),则 λ α = ( λ a x , λ a y , λ a z ) \lambda{\boldsymbol\alpha}=(\lambda{a_x},\lambda{a_y},\lambda{a_z}) λα=(λax,λay,λaz)
-
∣ λ α ∣ |\lambda\boldsymbol{\alpha}| ∣λα∣= ( λ a x ) 2 + ( λ a y ) 2 + ( λ a z ) 2 \sqrt{(\lambda a_{x})^2+(\lambda a_{y})^2+(\lambda a_{z})^2} (λax)2+(λay)2+(λaz)2= λ 2 ( a x 2 + a y 2 + a z 2 ) \sqrt{\lambda^2(a_x^2+a_y^2+a_z^2)} λ2(ax2+ay2+az2)= ∣ λ ∣ ∣ α ∣ |\lambda||\boldsymbol{\alpha}| ∣λ∣∣α∣
-
向量的数乘满足结合律和分配律
方程的思想求解向量相关问题
-
例如求空间中满足某个特征的点的坐标
-
使用建立方程并解方程的方法可以简化思维过程
-
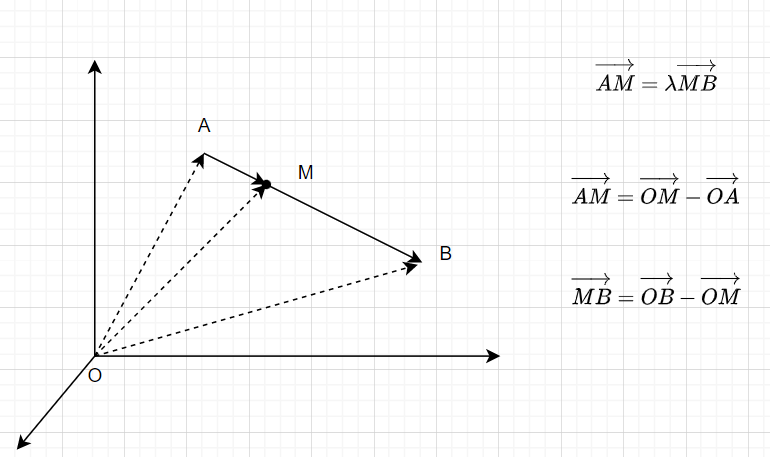
-
设 A M → = λ M B → \overrightarrow{AM}=\lambda\overrightarrow{MB} AM=λMB, A = ( x 1 , y 1 , z 1 ) , B = ( x 2 , y 2 , z 2 ) A=(x_1,y_1,z_1),B=(x_2,y_2,z_2) A=(x1,y1,z1),B=(x2,y2,z2)
-
其中:
- A M → \overrightarrow{AM} AM= O M → − O A → \overrightarrow{OM}-\overrightarrow{OA} OM−OA
- M B → \overrightarrow{MB} MB= O B → − O M → \overrightarrow{OB}-\overrightarrow{OM} OB−OM
-
所以 O M → − O A → = λ ( O B → − O M → ) \overrightarrow{OM}-\overrightarrow{OA} =\lambda(\overrightarrow{OB}-\overrightarrow{OM}) OM−OA=λ(OB−OM)
- ( 1 + λ ) O M → (1+\lambda)\overrightarrow{OM} (1+λ)OM= λ O B → + O A → \lambda\overrightarrow{OB}+\overrightarrow{OA} λOB+OA
- O M → \overrightarrow{OM} OM= 1 1 + λ ( O A → + λ O B → ) \frac{1}{1+\lambda}(\overrightarrow{OA}+\lambda\overrightarrow{OB}) 1+λ1(OA+λOB)= 1 1 + λ ( x 1 + λ x 2 , y 2 + λ y 2 , z 1 + λ z 2 ) \frac{1}{1+\lambda}(x_1+\lambda{x_2},y_2+\lambda{y_2},z_1+\lambda{z_2}) 1+λ1(x1+λx2,y2+λy2,z1+λz2)
向量的线性运算的坐标表示公式
-
利用坐标作向量的线性运算(加法,减法,数乘)是方便的
-
向量的坐标分解式对应了坐标在各个轴上的分量
-
利用相关交换律和结合律,可得
- a + b \boldsymbol{a+b} a+b= ( a x + b x ) i + ( a y + b y ) j + ( a z + b z ) k = ( a x + b x , a y + b y , a z + b z ) (a_x+b_x)\boldsymbol{i}+(a_y+b_y)\boldsymbol{j}+(a_z+b_z)\boldsymbol{k}=(a_x+b_x,a_y+b_y,a_z+b_z) (ax+bx)i+(ay+by)j+(az+bz)k=(ax+bx,ay+by,az+bz)
- a − b \boldsymbol{a-b} a−b= ( a x − b x ) i + ( a y − b y ) j + ( a z − b z ) k = ( a x − b x , a y − b y , a z − b z ) (a_x-b_x)\boldsymbol{i}+(a_y-b_y)\boldsymbol{j}+(a_z-b_z)\boldsymbol{k}=(a_x-b_x,a_y-b_y,a_z-b_z) (ax−bx)i+(ay−by)j+(az−bz)k=(ax−bx,ay−by,az−bz)
- λ a \lambda\boldsymbol{a} λa= λ ( a x , a y , a z ) \lambda(a_x,a_y,a_z) λ(ax,ay,az)
相关文章:

AM@向量代数@向量基本概念和向量线性运算
文章目录 abstract向量的基本概念向量向量的坐标分解式和坐标👺向量的模向量的长度(大小)👺零向量单位向量👺方向向量非零向量的单位向量正规化向量夹角👺 向量方向角和向量间夹角投影几何描述向量的线性运算向量的加减运算向量的…...
)
2023-11-08 LeetCode每日一题(最长平衡子字符串)
2023-11-08每日一题 一、题目编号 2609. 最长平衡子字符串二、题目链接 点击跳转到题目位置 三、题目描述 给你一个仅由 0 和 1 组成的二进制字符串 s 。 如果子字符串中 所有的 0 都在 1 之前 且其中 0 的数量等于 1 的数量,则认为 s 的这个子字符串是平衡子…...

Web3.0的测试题
任务: 在前端开发一个查询UI,查询当前用户账户的ETH余额和指定ERC20合约中的余额 目标: UI框架指定使用 MUI (https://mui.com)需要查询到当前账户的ETH余额并展示在UI界面上需要输入ERC20合约地址后,查询到到当前账户在此ERC20…...

Javascript知识点详解:对象的继承、原型对象、原型链
目录 对象的继承 原型对象概述 构造函数的缺点 prototype 属性的作用 原型链 constructor 属性 instanceof 运算符 构造函数的继承 多重继承 对象的继承 面向对象编程很重要的一个方面,就是对象的继承。A 对象通过继承 B 对象,就能直接拥有 B …...
学之思开源考试系统部署至Centos7
学之思开源考试系统部署至Centos7 1、下载源码 源码下载: https://gitee.com/mindskip/xzs-mysql 数据库脚本下载: https://www.mindskip.net:999/ 2、项目打包 分别在\source\vue\xzs-student目录和source\vue\xzs-admin目录,执行前端打…...

如何利用浏览器的可见性API优化网站性能
最近在使用微软AI聊天工具Bing时,发现一个有趣的东西。我向它提问后,它在持续输出的过程中,如果我离开了当前它的浏览器会话,比如切屏,看当前浏览器的其它标签页,它会默认停止它的输出,等我回来…...
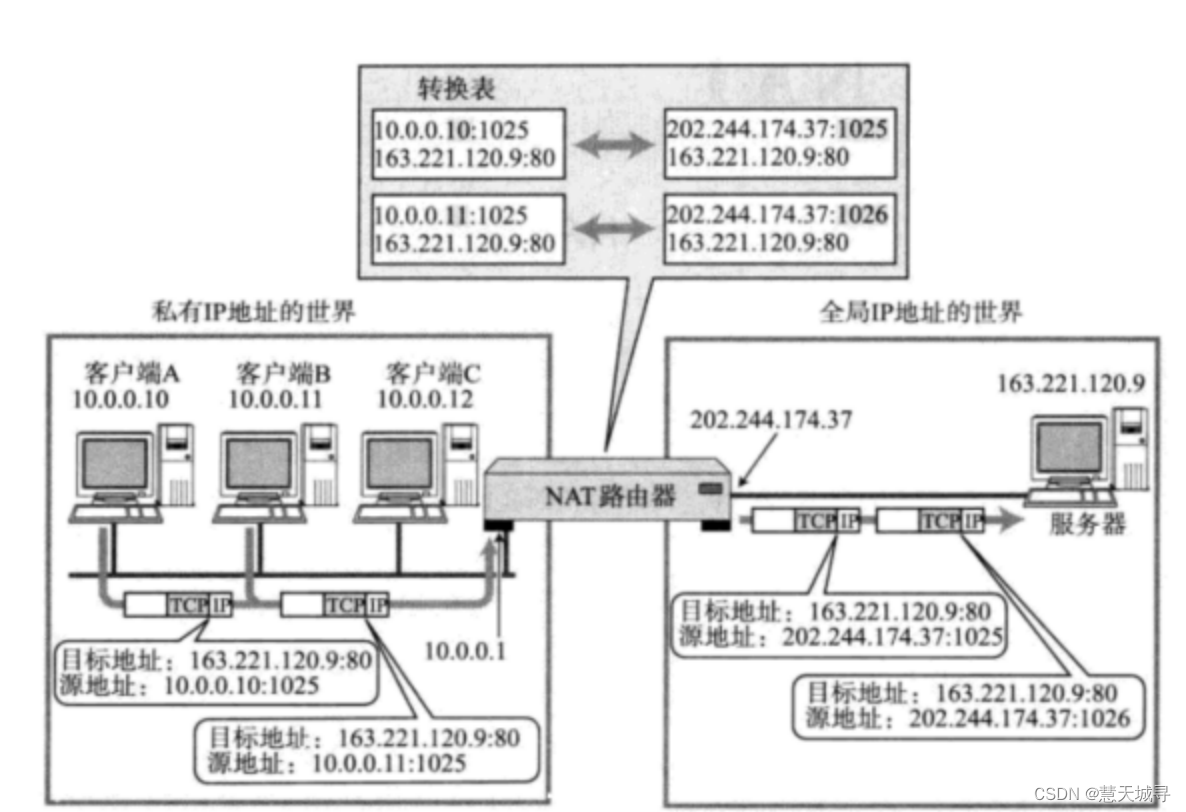
还不知道IP地址不够用是怎么被大牛们解决的?(NAT/NAPT, IPv6, DHCP)
文章目录 前言1. DHCP网络管理协议什么是 DHCPDHCP 两种分配机制 2. NAT网络地址转换协议什么是 NATNAT 技术使用NAT网络设备间如何通信两个内网设备相互通信不同内网中的设备相互通信NAT IP转换过程 NAPT 技术NAT 技术的缺陷 3. IPv6 协议什么是 IPv6 总结 前言 在之前的文章…...

使用决策树预测隐形眼镜类型
任务描述 本关任务:编写一个例子讲解决策树如何预测患者需要佩戴的隐形眼镜类型。使用小数据集,我们就可以利用决策树学到很多知识:眼科医生是如何判断患者需要佩戴的镜片类型,一旦理解了决策树的工作原理,我们甚至也…...

[ACTF2020 新生赛]BackupFile 1
题目环境: 好好好,让找源文件是吧?咱们二话不说直接扫它后台 使用dirsearch工具扫描网站后台(博主有这个工具的压缩包,可以私聊我领取)python dirsearch.py -u http://0d418151-ebaf-4f26-86b2-5363ed16530…...

解决vuex刷新数据丢失
Vuex 是一个 Vue.js 的状态管理库,它使得你可以在 Vue 组件之间共享状态。当你在 Vuex 中更新状态时,如果你遇到数据丢失或数据不一致的问题,可能需要进行深度复制或者使用其他方式来确保数据的完整性。 假设你有一个 Vuex 存储,…...
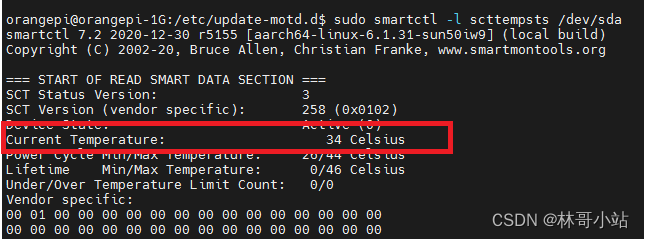
linux系统下读取当前硬盘的温度
这个其实很简单,借助于smartctl工具(Ubuntu默认安装好了),标红的部分就是当前温度,单位是摄氏度。 sudo smartctl -l scttempsts /dev/sda...
python 深度学习 解决遇到的报错问题8
本篇继python 深度学习 解决遇到的报错问题7-CSDN博客 目录 一、OSError: [WinError 127] 找不到指定的程序。 Error loading "D:\my_ruanjian\conda-myenvs\deeplearning\lib\site-packages\torch\lib\caffe2_detectron_ops.dll" or one of its dependencies. 二、…...
系统调用示例)
Linux pipe()系统调用示例
Linux系统调用pipe函数,创建一个pipe,通过传入的fd数组返回pipe的读、写两端。 其中fd[ 0 ]用于读,fd[ 1 ]用于写。 一个pipe是单向数据传输的,不用用于父子进程双向读写。创建2个pipe实现父子进程间的双线读写。 #include <u…...

音频中的采样率和比特率
音频中的采样率和比特率 采样频率千比特率音频比特率 采样频率 参考:https://blog.csdn.net/qq_38907791/article/details/88925224 采样频率,也称为采样速度或者采样率,定义了每秒从连续信号中提取并组成离散信号的采样个数,它…...

Python常用脚本
1.解压指定文件夹内的zip包,解压到当前位置 import os import zipfile# 指定文件夹路径 folder_path "/path/to/your/folder"# 获取文件夹下所有的zip文件 zip_files [os.path.join(folder_path, file) for file in os.listdir(folder_path) if file.e…...
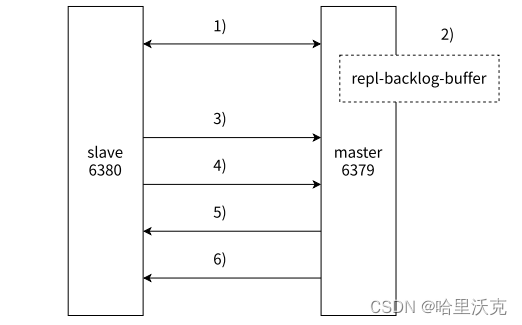
Redis5 分布式系统之主从模式
目录 分布式系统 引子 分布式系统类型 主从模式 一个主节点和多个从节点 创建多个节点方法 配置主从结构 主从模式知识 主从复制 拓扑结构 1.一主一从 2.一主多从 3.树形主从 主从实现原理 psync数据同步 全量复制和部分复制 psync流程 1.全量数据同步 2.部…...

【黑马程序员】Maven 进阶
文章目录 前言一、分模块开发与设计1. 分模块开发意义2. 分模块开发(模块拆分)2.1 创建 Maven 模块2.2 书写模块代码2.3 通过 Maven 指令安装模块到本地仓库(install 指令) 二、依赖管理1. 依赖传递1.1 依赖传递冲突问题 2. 可选依…...

231108 C语言memset当第三个参数为0,即设置个数为零也不报错
memset语法: void *memset(void *s, int c, size_t n); 犹豫第三个参数为0会不会报错,测试不会。 代码: #include"stdio.h" #include"stdlib.h" // memset memcpy int main() { int sig[100] { 0 }; int …...

HMM与LTP词性标注之马尔科夫模型(HMM原理剖析)
文章目录 问题描述viterbi算法联合概率与条件概率维特比算法实例 问题描述 viterbi算法 联合概率与条件概率 维特比算法实例...
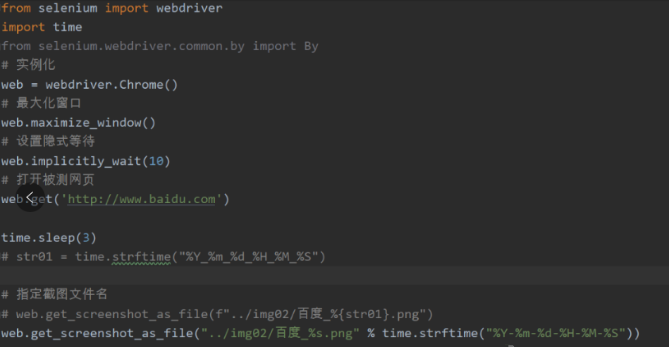
Python自动化测试selenium指定截图文件名方法
这篇文章主要介绍了Python自动化测试selenium指定截图文件名方法,Selenium 支持 Web 浏览器的自动化,它提供一套测试函数,用于支持 Web 自动化测试,下文基于python实现指定截图文件名方法,需要的小伙伴可以参考一下 前…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
