算法通过村第十八关-回溯|白银笔记|经典问题
文章目录
- 前言
- 组合总和问题
- 分割回文串
- 子集问题
- 排序问题
- 字母大小写全排列
- 单词搜索
- 总结
前言
提示:我不愿再给你写信了。因为我终于感到,我们的全部通信知识一个大大的幻影,我们每个人知识再给自己写信。 --安德烈·纪德
回溯主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列、棋盘等。这关我们就看看如何接入。
组合总和问题
参考题目地址:39. 组合总和 - 力扣(LeetCode)

如过不考虑重复的,这个题目和113的那个题目相差无疑,如果可以重复,哪呢是否可以无限制取下去呢?也不会,因为题目也给了说明。每个元素最小为1,因此最多一个target个1.我们画图该怎么做呢,对于序列{2,3,6,7}.target = 7.很明显我们选择1个2,还剩下target = 7 - 2 = 5.然后再选取一个2,还剩下target = target - 2 = 3;之后再选一个2,变成了target = target - 2 = 1,此时最小的为2,不能再选了,就要退出。看看有没有3。ok,有那么第一个结果就是{2,2,3}.
之后我们继续回退到只选1个2的时候,这是2不能选了,从{3,6,7}中选择,如下图所示,没有符合规定的。
依次类推,然后尝试从3和6、7中开始选择。
最终的结果就是{2,2,3}和{2,5}.为了方便,我们可以先对元素做个排序,然后按照上面的过程执行,形成一个树形图:
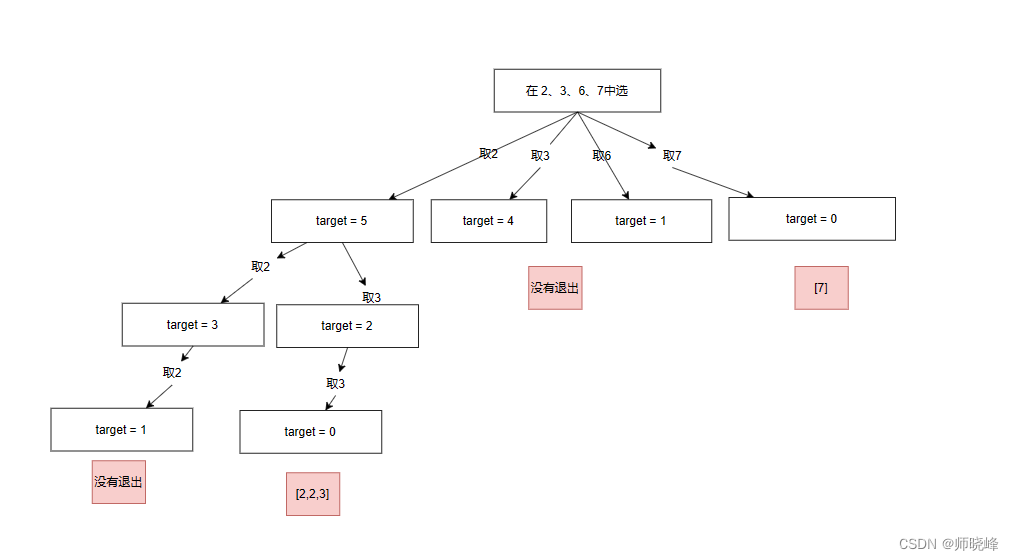
这个图横向是针对每个元素做暴力枚举,纵向是递归(向下找)也是纵横问题,实现起来代码也不复杂:
public List<List<Integer>> combinationSum(int[] c, int target) {List<List<Integer>> res = new ArrayList();List<Integer> path = new ArrayList();dfs(c,0,target,path,res);return res;
}public void dfs(int[] c,int u,int target,List<Integer> path,List<List<Integer>> res){if(target < 0){return;}if(target == 0){res.add(new ArrayList(path));return;}for(int i = u; i < c.length; i++){if(c[i] <= target){path.add(c[i]);dfs(c,i,target - c[i],path,res);path.remove(path.size() - 1);} }
}
分割回文串
参考题目地址:131. 分割回文串 - 力扣(LeetCode)
字符串如何判断回文本身就是一道算法题,本题在其之上还要解决一个问题:如何分割?如果暴力切割很麻烦,解决起来也很困难,如果从回溯的角度去思考就很清晰:
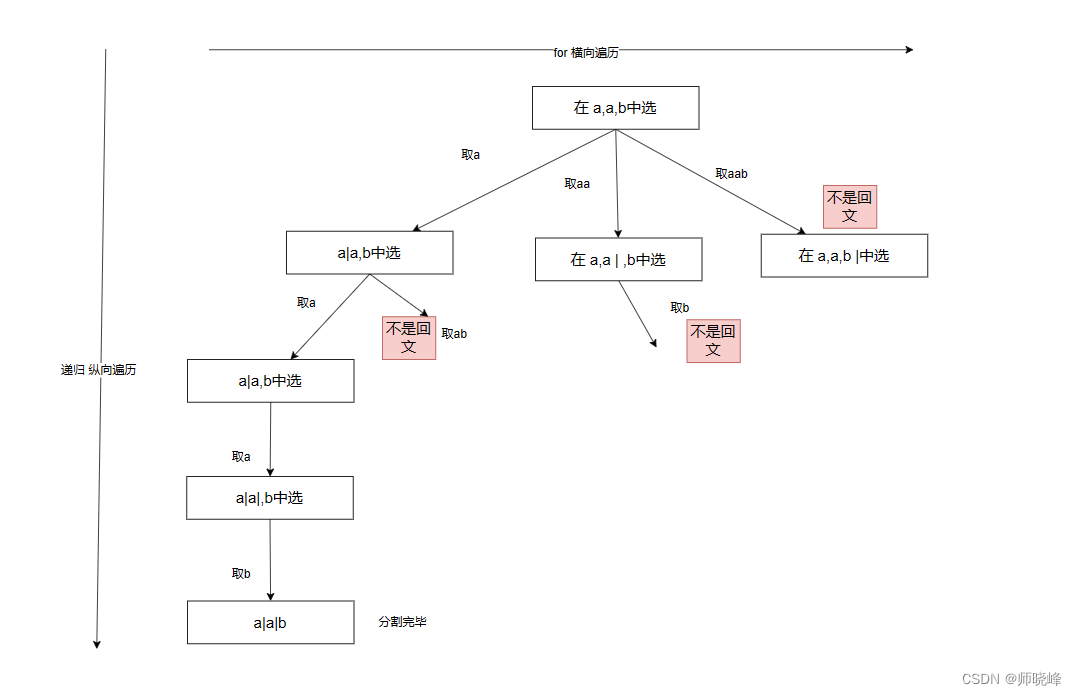
我们说回溯本身仍然回进行枚举的,这里也是一样的。切割线(途中的|)切割到字符串的结尾位置,说明找到了一个切割方法。这里就是先试一试,第一次切割’a’,第二次切割’aa‘,第三次切割’aab’。这对应的就是回溯里面的for循环(也就是横向遍历)
我们还要说回溯(需要进行递归操作)第一次切合’a’,剩下的就是‘ab’.递归就是在将其且下一个回文下来,也就是第二个‘a’,剩下的‘b’再交给递归进行一步切割。这就是纵向方面要干的事,依次类推。
至于回溯操作与前面的一样的道理,不再赘述。通过代码就可以发现,切割问题的回溯搜索的过程和嘴和问题的回溯搜索的过程是差不多的。
class Solution {List<List<String>> res = new ArrayList<>();Deque<String> path = new LinkedList<>();public List<List<String>> partition(String s) {backTracking(s,0);return res;}private void backTracking(String s, int startIndex) {// 如果起始位置大于s的大小,说明找到了一组分割方案if (startIndex >= s.length()) {res.add(new ArrayList<>(path));return;}for (int i = startIndex; i < s.length(); i++) {// 如果是回文子串,则记录if (isPalindrome(s, startIndex, i)) {String str = s.substring(startIndex, i + 1);path.addLast(str);} else {continue;} // 起始位置后移,保证不重复backTracking(s, i + 1);path.removeLast();}}public boolean isPalindrome(String str,int start,int end){for(int i = start, j = end; i < j; i++,j--){if(str.charAt(i) != str.charAt(j)){return false;}}return true;}
}
子集问题
子集问题也是回溯的经典使用场景。回溯可以画成一种状态树,子集,组合,分割,都可以抽象出来。
但是子集也有它特有的类型:需要找出所有情况。
参考题目:78. 子集 - 力扣(LeetCode)

画图详解:
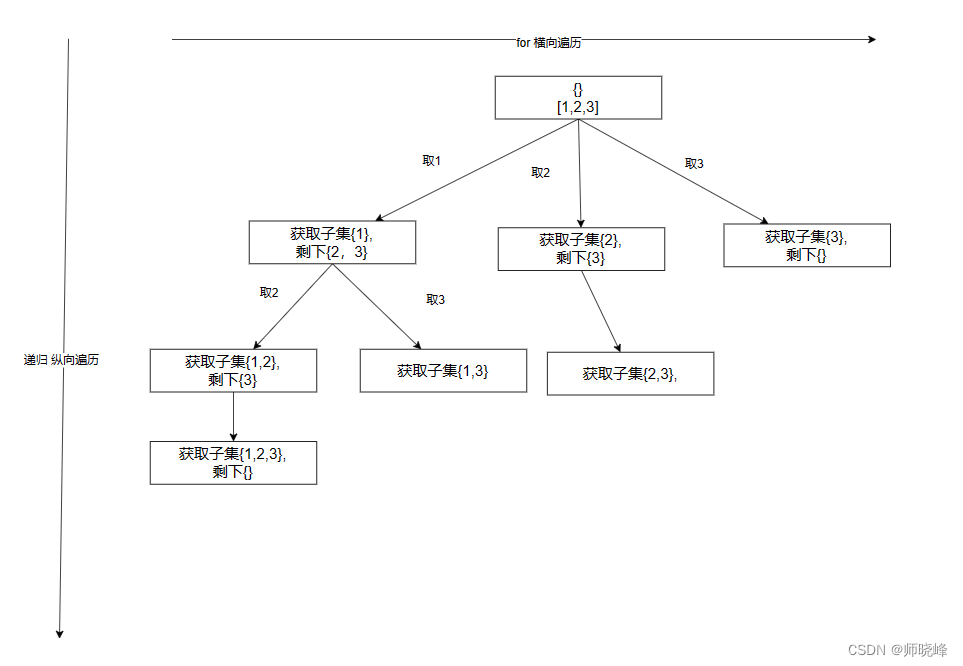
从图中也可以看出,遍历这颗树的时候,就可以记录下所有的节点,也就是得到子集结果。
那么什么时候停下来呢?起始可以不加终止条件,因为startIdex >= nums.size(),for循环就结束了。
记住:求子集问题,不需要任何的剪枝操作!因为子集就是要遍历整颗树。这样实现起来也比较容易。
class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList();public List<List<Integer>> subsets(int[] nums) {// 空集也是if(nums.length == 0 ){res.add(new ArrayList<>());return res;}backTracking(nums,0);return res;} public void backTracking(int[] nums,int startIndex){// 记住:加进来,再判断res.add(new ArrayList(path));if(startIndex >= nums.length){return;}for(int i = startIndex; i < nums.length; i++){// 今典小连招path.add(nums[i]);backTracking(nums,i+ 1);path.remove(path.size() - 1);}}
}
tips:上面的代码可以通过全局定义res和path,这样简介。这里(也可以转成参数传递的形式)
排序问题
参考题目介绍:46. 全排列 - 力扣(LeetCode)

排列问题也是经典的问题(每次刷是不是都难)。这个问题和前面的组合等问题的一个区别就是后面的还用再选(可重复),例如:1:开始使用了,但是到了2和3的时候仍然要使用一次。本质上是因为【1,2】和【2,1】从集合的角度看一个问题,单是从排列的角度是两个问题。
元素1在【1,2】中已经使用多了,但是在【2,1】中还要再使用一次,所以就不能使用startIndex了,此时可以使用一个used数组来标记已经选择的元素,完整的过程如图所示:
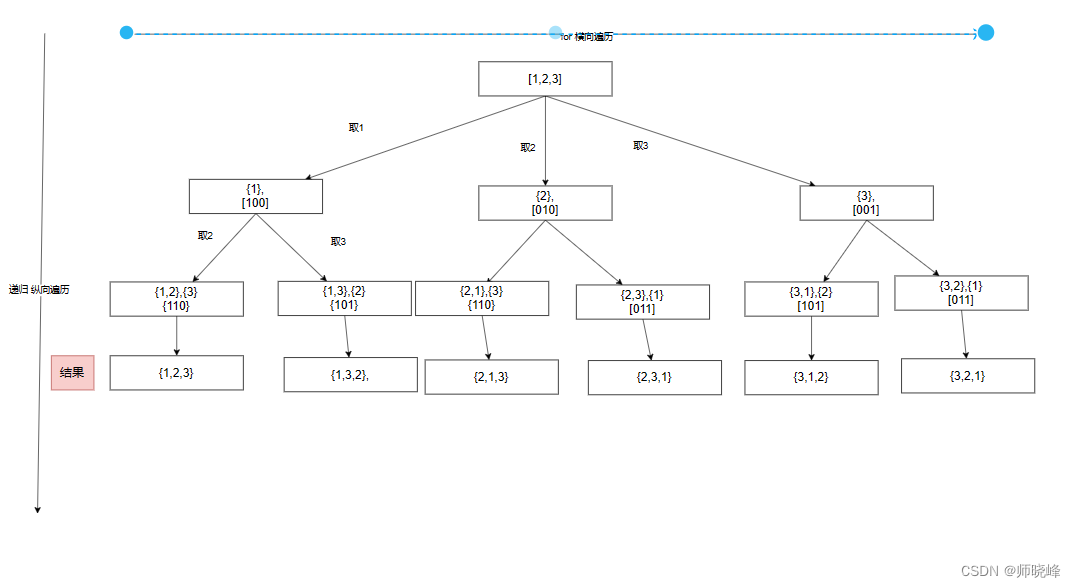
开图就知道了,怎么确定终止条件呢?就是到达叶子节点,那么是么时候到达叶子节点呢?
当时收集元素的数组path的大小达到和nums数组一样不就行了,说明就找到了一个全排列,也就是到达叶子节点了。
class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> path = new ArrayList<>();// 是否选boolean[] used ; public List<List<Integer>> permute(int[] nums) {if(nums.length == 0){return res;}used = new boolean[nums.length];permuteHepler(nums);return res;}public void permuteHepler(int[] nums){if(path.size() == nums.length){res.add(new ArrayList<>(path));return ;}for(int i = 0; i < nums.length; i++){// 解决01 10 问题if(used[i]){continue;}used[i] = true;path.add(nums[i]);permuteHepler(nums);// 经典回溯path.remove(path.size() - 1);used[i] = false;}}
}
字母大小写全排列
参考题目地址:784. 字母大小写全排列 - 力扣(LeetCode)

如果本题去掉数组,只告诉你两个字母ab,然你每个字母变化大小写,那么就是ab,Ab,aB,AB四种情况。就和上面的处理一样了。这里有数字的干扰,我们就需要作过滤数字,只处理字母。还有就是添加大小写的转换问题了。

由于每个字符的大小形式刚好相差32,因此再大小写里面可以换成用c^32来进行转换和恢复。这样代码就简洁多了:
class Solution {List<String> res = new ArrayList<>();public List<String> letterCasePermutation(String s) {dfs(s.toCharArray(),0);return res;}public void dfs(char[] arr, int pos){// 过滤数字while(pos < arr.length && Character.isDigit(arr[pos])){pos++;}// 终止条件if(pos == arr.length){res.add(new String(arr));return;}// 转换arr[pos]^=32;dfs(arr,pos + 1);// 撤销arr[pos]^=32;dfs(arr,pos + 1);}
}
单词搜索
参考题目介绍:79. 单词搜索 - 力扣(LeetCode)

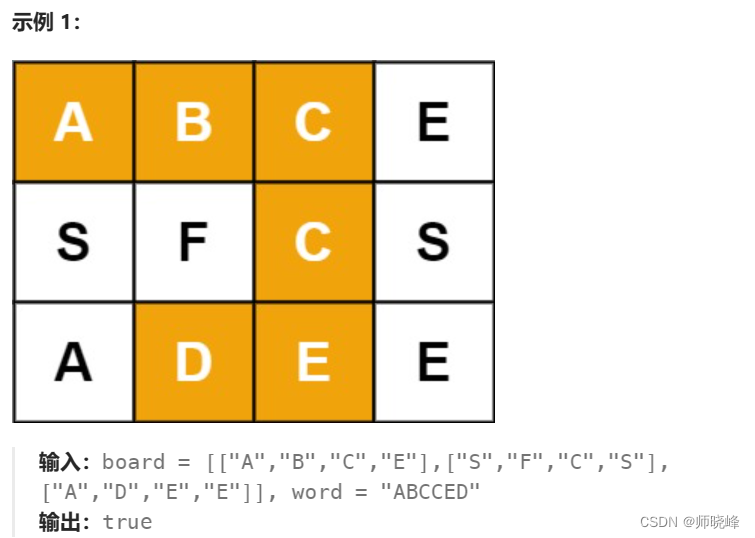
思路:从上到下,左到右遍历网格,每个坐标递归调用check(i,j,k)函数,i,j表示网格坐标,k表示word的第k个字符,如果能搜索到第k个字符返回true,否则返回false。
check函数的终止条件也很明确:
- 如果i,j的位置和字符上的字符位置k不相符,也就是说这个方面的路径有问题,直接返回false
- 如果搜索到了字符串的结尾,则找到了网格中的一条路径,这条路径上的字符正好可以组成字符串s,返回true。
两种情况都不满足,就把当前网格加入visited数组,visited表示该位置已经访问过了,然后顺着当前网格的坐标的四个方向继续尝试,如果没有找到k开始的子串,则返回回溯状态visited[i ] [j] = false,继续向后面访问。
分析一波复杂度:时间复杂度为O(ML*3^L),M,N 为网格的长度和宽度,L 为字符串word的长度,第一次电泳check函数的时候,回向4个方向进行测试,其余坐标的节点都是3个方向检车,走过的分支不会反方向回去,左移check函数的复杂度为3^L,而网格上面有MN个坐标,且存在剪枝,最坏的情况下是O(MN * 3 ^L).空间复杂符是O(MN) visited数组的空间是O(MN) ,check递归栈的最大深度在最坏的情况下是O(MN)
class Solution {public boolean exist(char[][] board, String word) {char[] words = word.toCharArray();for(int i = 0; i < board.length; i++){for(int j = 0; j < board[i].length;j++){if(dfs(board,words,i,j,0)){return true;}}}return false;}public boolean dfs(char [][] board,char[] words,int i,int j, int k){// 边界+条件if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != words[k]){return false;}// 终止条件if(k == words.length - 1){return true;}// 防止重复board[i][j] = '\0';boolean res = dfs(board,words,i+1,j,k+1) || dfs(board,words,i - 1,j,k+1) || dfs(board,words,i,j - 1,k+1) || dfs(board,words,i,j+ 1,k+1);// 恢复board[i][j] = words[k];return res;}
}
总结
提示:组合总和问题;分割问题;子集问题;排列问题;搜索问题
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。

相关文章:

算法通过村第十八关-回溯|白银笔记|经典问题
文章目录 前言组合总和问题分割回文串子集问题排序问题字母大小写全排列单词搜索总结 前言 提示:我不愿再给你写信了。因为我终于感到,我们的全部通信知识一个大大的幻影,我们每个人知识再给自己写信。 --安德烈纪德 回溯主要解决一些暴力枚举…...

vue2 集成 - 超图 - SuperMap iClient3D for WebGL 及常用方法
文章目录 1:下载SuperMap iClient3D for WebGL2:格式化项目中所用的依赖包3:vue2 项目引入4:vue2 页面使用常见方法4.1 创建三维场景,引入在线地图资源,定位到指定位置4.2 坐标拾取4.3 用户输入事件4.4 拾取实体4.5 实体改变监听事件4.6 双击全屏4.7 相机移动事件4.8 添加…...

应用程序服务器/事件驱动编程/CommonJS介绍
目录 应用程序服务器事件驱动编程CommonJS 👍 点赞,你的认可是我创作的动力! ⭐️ 收藏,你的青睐是我努力的方向! ✏️ 评论,你的意见是我进步的财富! 应用程序服务器 应用程序服务器是一种用…...

第二十九章 目标检测中的测试模型评价指标(车道线感知)
前言 近期参与到了手写AI的车道线检测的学习中去,以此系列笔记记录学习与思考的全过程。车道线检测系列会持续更新,力求完整精炼,引人启示。所需前期知识,可以结合手写AI进行系统的学习。 介绍 自动驾驶的一大前提是保证人的安全…...
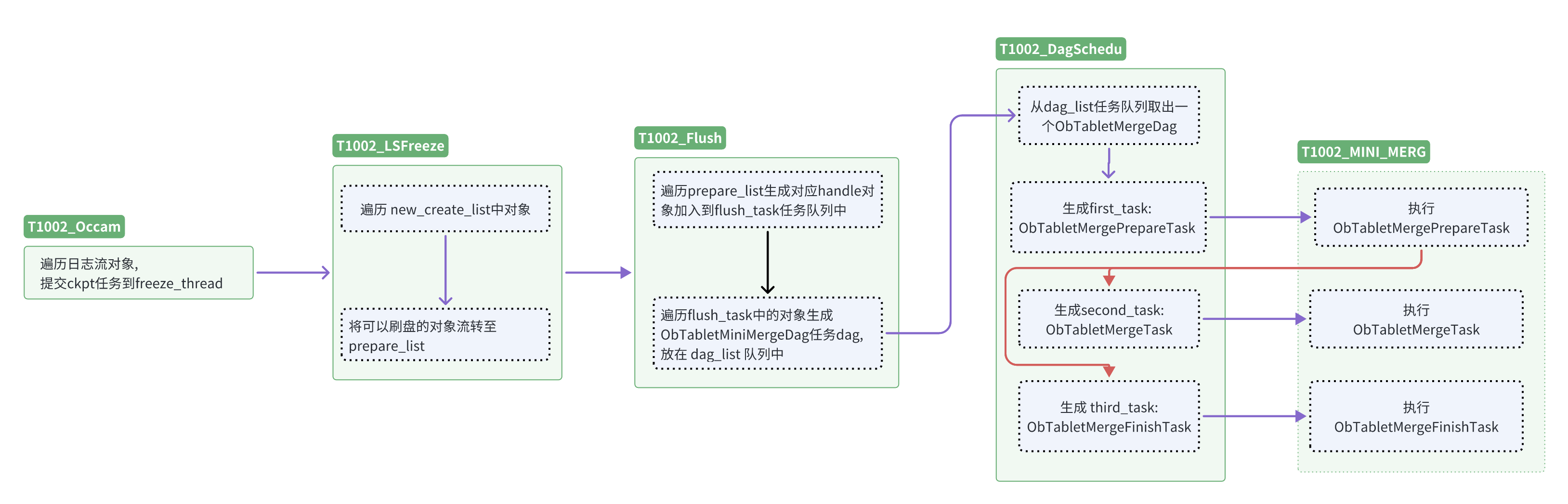
OceanBase 如何通过日志观测冻结转储流程?
本文旨在通过日志解析 OceanBase 的冻结转储流程,以其冻结检查线程为切入点,以租户(1002)的线程名为例。 作者:陈慧明,爱可生测试工程师,主要参与 DMP 和 DBLE 自动化测试项目。 爱可生开源社区…...

深度图(Depth Map)
文章目录 深度图深度图是什么深度图的获取方式激光雷达或结构光等传感器的方法激光雷达RGB-D相机 双目或多目相机的视差信息计算深度采用深度学习模型估计深度 深度图的应用场景扩展阅读 深度图 深度图是什么 深度图(depth map)是一种灰度图像…...

Ubuntu下Anaconda安装
Ubuntu下Anaconda安装 进入anaconda官网 https://www.anaconda.com/ 下载Linux64位版本; 将下载好的".sh"文件放入虚拟机中; 运行指令sudo bash Anaconda3-2023.09-0-Linux-x86_64.sh 此后会自动加载安装程序,中途会停止两次&am…...
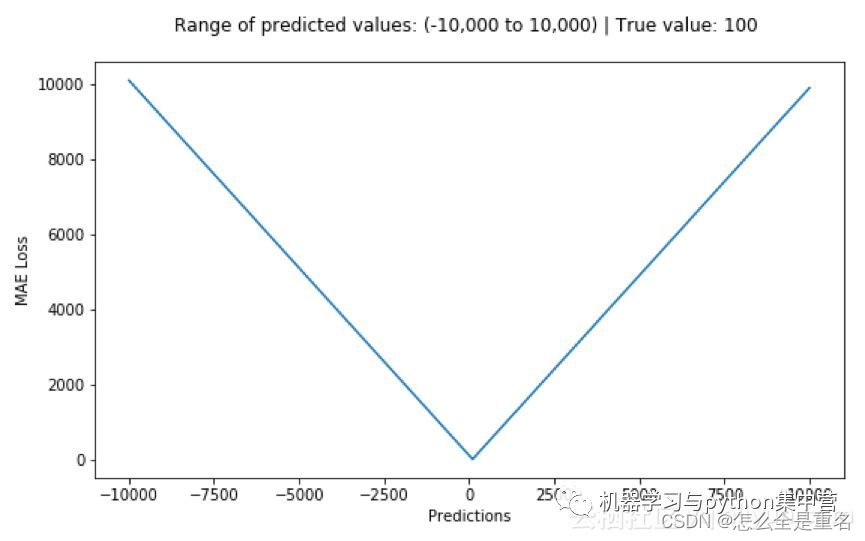
目标检测回归损失函数(看情况补...)
文章目录 L1 loss-平均绝对误差(Mean Absolute Error——MAE)L2 loss-均方误差(Mean Square Error——MSE)Smooth L1 LossMAE、MSE、Smooth L1对比IoU LossGIoU LossDIoU Loss、CIoU LossE-IoU Loss、Focal E-IoU LossReferenceL1 loss-平均绝对误差(Mean Absolute Error——…...
将 Figma 轻松转换为 Sketch 的免费方法
最近浏览网站的时候,发现很多人不知道Figma是怎么转Sketch的。众所周知,Figma支持Sketch文件的导入,但不支持Sketch的导出,那么Figma是如何转Sketch的呢?不用担心,建议使用神器即时设计。它是一个可以实现在…...

GPU推理提速4倍!FlashDecoding++技术加速大模型推理
推理大模型(LLM)是AI服务提供商面临的巨大经济挑战之一,因为运营这些模型的成本非常高。FlashDecoding 是一种新的技术,旨在解决这一问题,它通过提高LLM推理速度和降低成本,为使用大模型赚钱提供了新的可能…...
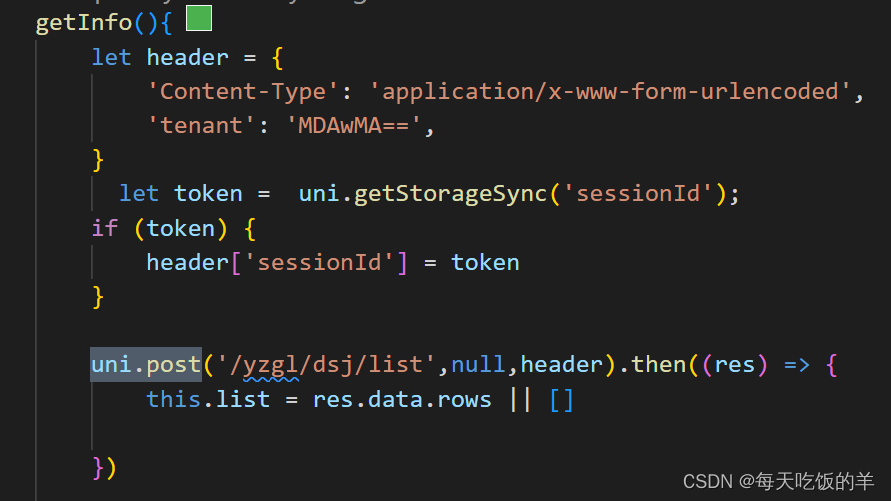
class类默认导出,header字段在请求中的位置
这是封装好的,没封装的如下 如果没有用uni.post那么就是如下的结构 let header {Content-Type: application/x-www-form-urlencoded,tenant: MDAwMA, } request({url:/sal/formula/validFormula,method:post,data:{},header })...

PHP将pdf转为图片后用OCR识别
1.确保apt包是最新 sudo apt update 2.使用apt安装 sudo apt install tesseract-ocr 3.检查版本 tesseract --version 4.pdf转成图片,这边需要安装imagick插件 $pdf new Imagick(); $pdf->setResolution(150, 150); $pdf->readImage(..$temp); $pdf->…...

IDEA 函数下边出现红色的波浪线,提示报错
Inferred annotations: Method makeOkResult: org.jetbrains.annotations.Contract("_, _, _, _ -> new") org.jetbrains.annotations.NotNull Parameter headers: org.jetbrains.annotations.NotNull 出现这个提示,我应该怎么处理这个函数࿱…...
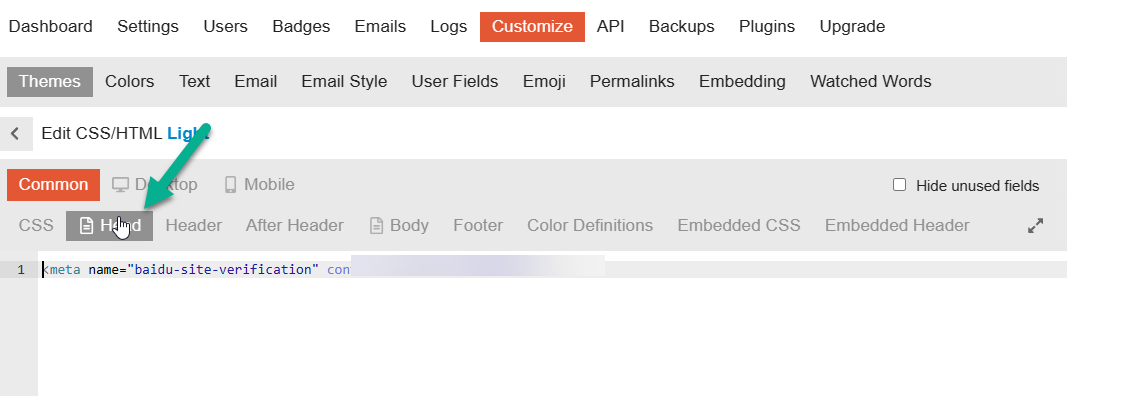
Discourse 如何在 header 上添加 HTML
虽然现在大部分网站都开始支持使用 CDN 的网站校验了。 但还有些网站在你需要他们提供服务的时候要求使用 header 的 meta 数据校验。 Discourse 是可以轻松的实现上面的功能的。 添加方法 选择你的 Discourse 网站下的自定义。 然后在左侧选择你需要添加的主题。 为了方便…...

[深入理解SSD] 总目录
SSD 综述 [SSD综述 1.1] 导论_SSD让开机击败99%的电脑 [SSD综述 1.2] 固态硬盘(SSD)和机械硬盘(HDD)区别对比介绍? [SSD综述 1.3] SSD及固态存储技术30年简史 [SSD综述 1.4] SSD固态硬盘的结构 [SSD综述 1.5] SSD 主控和固件核心功能详解 [S…...
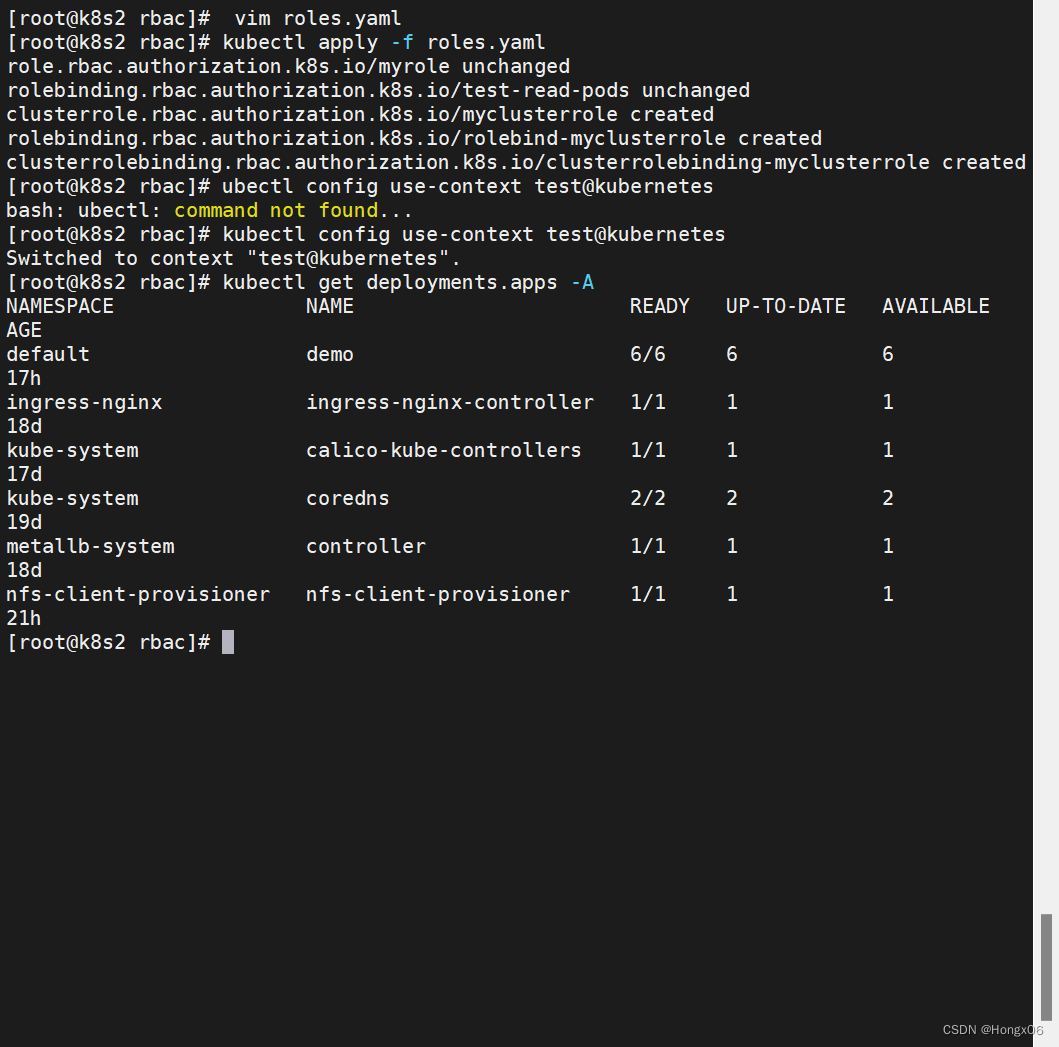
kubernetes集群编排(7)
目录 k8s认证授权 pod绑定sa 认证 授权 k8s认证授权 pod绑定sa [rootk8s2 ~]# kubectl create sa admin //在当前 Kubernetes 集群中创建一个名为 "admin" 的新服务账户[rootk8s2 secret]# vim pod3.yaml apiVersion: v1 kind: Pod metadata:name: mypod spec…...

mfc 下的OpenGL
建立一个SDI 的MFC工程,然后按freeglut 在mfc 下的编译_leon_zeng0的博客-CSDN博客 一文设置好include lib 路径 在view 中建立这2个函数: // Standard OpenGL Init StuffBOOL CmfcOpenglDemoView::SetupPixelFormat() {static PIXELFOR…...

机器翻译目前广泛应用于文档翻译以及硬件翻译
机器翻译(Machine Translation,MT)是一种自动化技术,用于将一种语言的文本转换为另一种语言的文本。它通常被用于跨语言交流和全球化的需求。 机器翻译目前可分为软件和硬件,软件常用的则是文档翻译、文字翻译、图片翻…...

木材加工工厂数字孪生可视化管理平台,赋能传统木材制造业数字化高质转型
数字化是当今经济发展的主流话题,以赋能传统制造业转型升级的需求最为迫切、效果最为显著。目前世界各国正积极发力智能制造,力求争夺智能制造领先位置,而构建适应传统制造业转型的数字化平台成为当务之急。数字化、智能化已成为木材加工行业…...

企业级低代码开发,科技赋能让企业具备“驾驭软件的能力”
科技作为第一生产力,其强大的影响力在各个领域中都有所体现。数字技术,作为科技领域中的一股重要力量,正在对传统的商业模式进行深度的变革,为各行业注入新的生命力。随着数字技术的不断发展和应用,企业数字化转型的趋…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
