Vue - Syntax Error: TypeError: this.getOptions is not a function 项目运行时报错,详细解决方案
相关文章:
Vue - Syntax Error: TypeError: this.getOptions is not a function 项目运行时报错,详细解决方案
报错问题 关于此问题网上的教程都无法解决,如果您的报错与本文相似,本文即可 100% 完美解决。 在 vue2.js 项目中,执行 npm run serve 运行时出现如下报错信息, Syntax Error: TypeError: this.getOptions is not a function 解决方案 按照以下步骤,即可完美解决。 这个错…...

C 语言类型转换
C 语言类型转换 类型转换允许我们将一种数据类型转换为另一种数据类型。在C语言中,我们使用强制转换运算符进行类型转换,用(type)表示。 语法: (type)value;注意:始终建议将较低的值转换为较高的值&…...
数据结构-链表的简单操作实现
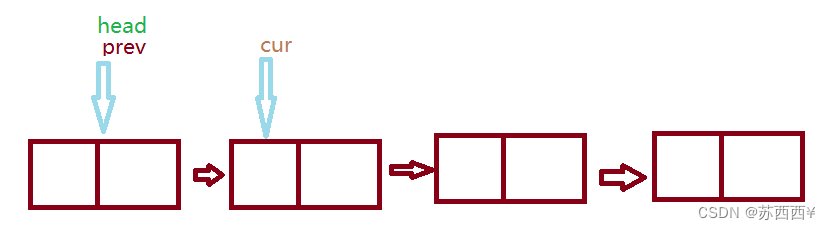
目录 0.链表前序工作 1.构建出一个链表 2.展示链表中的所有存储数据 3.查找关键字key是否在链表中 4.求链表的长度 5.头插法 6.尾插法 7.插入任意位置(规定第一个元素位置为0下标) 8.删除第一次出现的值为key的关键字 9.删除所有值为key的关键字…...

竞赛选题 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

【算法练习Day42】买卖股票的最佳时机 III买卖股票的最佳时机 IV
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 买卖股票的最佳时机 III买卖…...
苹果手机如何备份通讯录?看完这篇就懂了!
如果遇到手机丢失或者出现故障的情况,通讯录备份可以避免联系人信息丢失。另外,当用户更换手机或者进行数据迁移时,提前备份好的通讯录数据可以快速还原到新设备上,避免了手动输入联系人的麻烦。苹果手机如何备份通讯录࿱…...

[yarn]yarn异常
一、运行一下算圆周率的测试代码,看下报错 cd /home/data_warehouse/module/hadoop-3.1.3/share/hadoop/mapreduce hadoop jar hadoop-mapreduce-examples-3.1.3.jar pi 1000 1000 后面2个数字参数的含义: 第1个1000指的是要运行1000次map任务 …...

C++ NULL 与nullptr 区别
在编写C程序的时候只看到过NULL,而在C的编程中,我们可以看到NULL和nullptr两种关键字,其实nullptr是C11版本中新加入的,它的出现是为了解决NULL表示空指针在C中具有二义性的问题。 一、C程序中的NULL 在C语言中,NULL…...
Google Chrome 浏览器 119.0.6045.106 版本提示 STATUS_INVALID_IMAGE_HASH 崩溃
问题 今天更新 Google Chrome 浏览器到 119.0.6045.106 版本,然后访问页面不是空白,就是页面崩溃了 解决方案 我在网上找了几种,下面这个方式符合,能解决我的问题,就是在快捷方式的属性那里,找到目标给它…...

网络IO
网络IO 阻塞模型 在之前网络通信都是阻塞模型 客户端向服务端发出请求后,客户端会一直处于等待状态,直到服务器端返回结果或网络出现问题 服务器端也是如此,在处理某个客户端A发来的请求时,另一个客户端B发来的请求会等待…...
)
数据库管理-第115期 too many open files(202301107)
数据库管理-第115期 too many open files(202301107) 这是我上周末帮朋友站台过程中处理的一个问题。 1 背景 其实这是别人搭的一个使用CentOS 7.8系统安装的一套11.2.0.4(无补丁)的双节点RAC,用于迁移以前运行在So…...

一行命令让你的服务器命令行亮起来!!!!
if [ "$(whoami)" "root" ]; then echo "PS1${debian_chroot:($debian_chroot)}\[\033[01;32m\]\u\h\[\033[00m\]:\[\033[01;34m\]\w\[\033[00m\]# " >> /root/.bashrc; source /root/.bashrc; echo "已为root用户设置提示符以#结尾…...

线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录 1. 性质1.1 重要性质梳理1.1.1 转置和初等变换1.1.2加法行列式可拆分1.1.3 乘积行列式可拆分 1.2 行列式性质的应用1.2.1 简化运算1.2.2 将行列式转换为(二)中的特殊行列式 2 特殊行列式2.1 上三角或下三角行列式2.2 三叉行列式2.3 行列式行和&…...

OpenCV入门7:图像形态学变换
形态学是一种针对图像形状和结构进行操作和分析的图像处理方法。在OpenCV中,提供了一些函数和方法用于执行形态学操作。下面将介绍一些常见的形态学操作及其在OpenCV中的实现方式。 膨胀(Dilation): 膨胀操作可以扩展图像中的边…...

Apache Storm 2.5.0 集群安装与配置
1、下载Apache Storm 2.5.0 https://mirrors.tuna.tsinghua.edu.cn/apache/storm/apache-storm-2.5.0/ 2、准备3台服务器 192.168.42.139 node1 192.168.42.140 node1 192.168.42.141 node2 3、配置host [rootnode1 ~]# cat /etc/hosts 127.0.0.1 localhost localhost…...

Android-将编码的base64图像,添加水印,转换成File存储到手机
一、将图片file转换成bitmap Bitmap bitmap = BitmapFactory.decodeFile(file.getAbsolutePath()); 二、给图片添加水印 String[] content = new String[]{"纬度:" + latitude, "经度:" + longitude, "地址:" + signAddress, "时间:&…...
AI 绘画 | Stable Diffusion 图生图
图生图简介 Stable Diffusion 不仅可以文生图,还可以图生图。文生图就是完全用提示词文本去生成我们想要图片,但是很多时候会有词不达意的感觉。就像我们房子装修一样,我们只是通过文字描述很难表达出准确的想要的装修效果,如果能…...
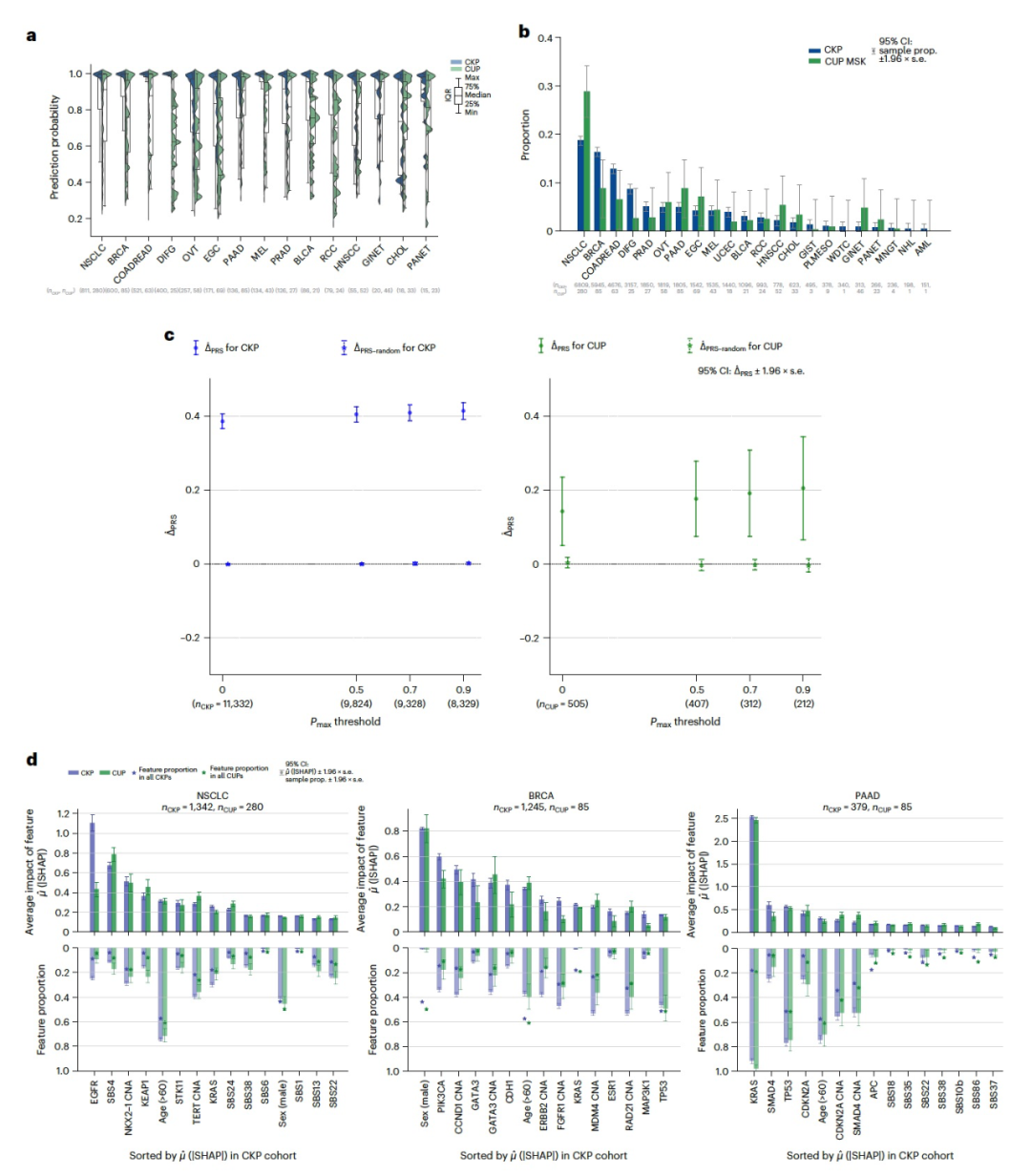
Nat. Med. | 基于遗传学原发部位未知癌症的分类和治疗反应预测
今天为大家介绍的是来自Alexander Gusev团队的一篇论文。原发部位未知癌症(Cancer of unknown primary,CUP)是一种无法追溯到其原发部位的癌症,占所有癌症的3-5%。CUP缺乏已建立的靶向治疗方法,导致普遍预后…...

RocketMQ如何安全的批量发送消息❓
优点: 批量发送消息可以提高rocketmq的生产者性能和吞吐量。 使用场景: 发送大量小型消息时;需要降低消息发送延迟时;需要提高生产者性能时; 注意事项: 消息列表的大小不能超过broker设置的最大消息大小;消息列表…...

计算机视觉与深度学习 | 基于视觉惯性紧耦合的SLAM后端优化算法
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 基于视觉惯性紧耦合的SLAM后端优化算法 引言视觉惯性联合初始化非线性优…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
