一文搞懂Python时间序列
Python时间序列
- 1. datetime模块
- 1.1 datetime对象
- 1.2 字符串和datatime的相互转换
- 2. 时间序列基础
- 3. 重采样及频率转换
- 4. 时间序列可视化
- 5. 窗口函数
- 5.1 移动窗口函数
- 5.2 指数加权函数
- 5.3 二元移动窗口函数
时间序列(Time Series)是一种重要的结构化数据形式。时间序列的数据意义取决于具体的应用场景,主要有以下几种:
- 时间戳(timestamp):特定的时刻
- 固定时期(period):2007年1月或2010年全年
- 时间间隔(interval):由起始和结束时间戳表示。时期(period)可以被看作间隔的特例。
1. datetime模块
1.1 datetime对象
datetime.datetime对象(以下简称datetime对象)以毫秒形式存储日期和时间。datetime.timedelta表示datetime对象之间的时间差。
import pandas as pd
import numpy as np
from datetime import datetime,timedelta
%matplotlib inline
now = datetime.now() #now为datetime.datetime对象
now
输出:
datetime.datetime(2019, 10, 11, 15, 33, 5, 701305)
now.year,now.month,now.day
输出:
(2019, 10, 11)
delta = datetime.now()-datetime(2019,1,1) #delta为datetime.timedelta对象
datetime.now() + timedelta(12)
输出:
datetime.datetime(2023, 3, 10, 22, 13, 25, 3470)
1.2 字符串和datatime的相互转换
(1) 利用str或datetime.strftime方法(传入一个格式化字符串),datetime对象和pandas的Timestamp对象可以被格式化为字符串;datetime.strptime可以将字符串转换为日期。
stamp = datetime(2011,1,3)
stamp.strftime('%Y-%m-%d') #或str(stamp)
输出:
‘2011-01-03’
datetime.strptime('2019-10-01','%Y-%m-%d')
输出:
datetime.datetime(2019, 10, 1, 0, 0)
(2) 对于一些常见的日期格式,可以使用datautil中的parser.parse方法(不支持中文)
from dateutil.parser import parse
parse('2019-10-01') #形成datetime.datetime对象
输出:
datetime.datetime(2019, 10, 1, 0, 0)
(3) pandas的to_datetime方法可以解析多种不同的日期表示形式
import pandas as pd
datestrs = ['7/6/2019','8/6/2019']
dates = pd.to_datetime(datestrs) #将字符串列表转换为Timestamp对象
type(dates)
输出:
pandas.core.indexes.datetimes.DatetimeIndex
dates[0]
输出:
Timestamp(‘2019-07-06 00:00:00’)
2. 时间序列基础
pandas最基本的时间序列类型就是以时间戳(通常以Python字符串或datetime对象表示)为索引的Series。
时期(period)表示的是时间时区,比如数日、数月、数季、数年等。
from datetime import datetimedates = [datetime(2019,1,1),datetime(2019,1,2),datetime(2019,1,5),datetime(2019,1,10),datetime(2019,2,10),datetime(2019,10,1)]ts = pd.Series(np.random.randn(6),index = dates) #ts就成为一个时间序列,datetime对象实际上是被存放在一个DatetimeIndex中
ts
输出:
2019-01-01 1.175755
2019-01-02 -0.520842
2019-01-05 -0.678080
2019-01-10 0.195213
2019-02-10 2.201572
2019-10-01 0.115911
dtype: float64
dates = pd.DatetimeIndex(['2019/01/01','2019/01/02','2019/01/02','2019/5/01','3/15/2019']) #同一时间点上多个观测数据
dup_ts = pd.Series(np.arange(5),index = dates)
dup_ts
输出:
2019-01-01 0
2019-01-02 1
2019-01-02 2
2019-05-01 3
2019-03-15 4
dtype: int32
dup_ts.groupby(level = 0).count()
输出:
2019-01-01 1
2019-01-02 2
2019-03-15 1
2019-05-01 1
dtype: int64
pd.date_range可用于生成指定长度的DatetimeIndex
pd.date_range('2019/01/01','2019/2/1') #默认情况下产生按天计算的时间点。
输出:
DatetimeIndex([‘2019-01-01’, ‘2019-01-02’, ‘2019-01-03’, ‘2019-01-04’,
‘2019-01-05’, ‘2019-01-06’, ‘2019-01-07’, ‘2019-01-08’,
‘2019-01-09’, ‘2019-01-10’, ‘2019-01-11’, ‘2019-01-12’,
‘2019-01-13’, ‘2019-01-14’, ‘2019-01-15’, ‘2019-01-16’,
‘2019-01-17’, ‘2019-01-18’, ‘2019-01-19’, ‘2019-01-20’,
‘2019-01-21’, ‘2019-01-22’, ‘2019-01-23’, ‘2019-01-24’,
‘2019-01-25’, ‘2019-01-26’, ‘2019-01-27’, ‘2019-01-28’,
‘2019-01-29’, ‘2019-01-30’, ‘2019-01-31’, ‘2019-02-01’],
dtype=‘datetime64[ns]’, freq=‘D’)
pd.date_range('2010/01/01',periods = 30) # 传入起始或结束日期及一个表示时间段的数字。
输出:
DatetimeIndex([‘2010-01-01’, ‘2010-01-02’, ‘2010-01-03’, ‘2010-01-04’,
‘2010-01-05’, ‘2010-01-06’, ‘2010-01-07’, ‘2010-01-08’,
‘2010-01-09’, ‘2010-01-10’, ‘2010-01-11’, ‘2010-01-12’,
‘2010-01-13’, ‘2010-01-14’, ‘2010-01-15’, ‘2010-01-16’,
‘2010-01-17’, ‘2010-01-18’, ‘2010-01-19’, ‘2010-01-20’,
‘2010-01-21’, ‘2010-01-22’, ‘2010-01-23’, ‘2010-01-24’,
‘2010-01-25’, ‘2010-01-26’, ‘2010-01-27’, ‘2010-01-28’,
‘2010-01-29’, ‘2010-01-30’],
dtype=‘datetime64[ns]’, freq=‘D’)
pd.date_range('2010/01/01','2010/12/1',freq = 'BM') #传入BM(business end of month),生成每个月最后一个工作日组成的日期索引
输出:
DatetimeIndex([‘2010-01-29’, ‘2010-02-26’, ‘2010-03-31’, ‘2010-04-30’,
‘2010-05-31’, ‘2010-06-30’, ‘2010-07-30’, ‘2010-08-31’,
‘2010-09-30’, ‘2010-10-29’, ‘2010-11-30’],
dtype=‘datetime64[ns]’, freq=‘BM’)
pd.Series(np.arange(13),index = pd.date_range('2010/01/01','2010/1/3',freq = '4h'))
输出:
2010-01-01 00:00:00 0
2010-01-01 04:00:00 1
2010-01-01 08:00:00 2
2010-01-01 12:00:00 3
2010-01-01 16:00:00 4
2010-01-01 20:00:00 5
2010-01-02 00:00:00 6
2010-01-02 04:00:00 7
2010-01-02 08:00:00 8
2010-01-02 12:00:00 9
2010-01-02 16:00:00 10
2010-01-02 20:00:00 11
2010-01-03 00:00:00 12
Freq: 4H, dtype: int32
period_range可用于创建规则的时期范围
pd.Series(np.arange(10),index = pd.period_range('2019/1/1','2019/10/01',freq='M'))
输出:
2019-01 0
2019-02 1
2019-03 2
2019-04 3
2019-05 4
2019-06 5
2019-07 6
2019-08 7
2019-09 8
2019-10 9
Freq: M, dtype: int32
3. 重采样及频率转换
重采样(resampling)指的是将时间序列从一个频率转换到另一个频率的处理过程。
- 降采样(downsampling):将高频率数据聚合到低频率数据
- 升采样(upsampling):将低频率数据转换到高频率
rng = pd.date_range('2019/01/01',periods = 100,freq='D')
ts = pd.Series(np.random.randn(len(rng)),index=rng)
ts.resample('M').mean()
输出:
2019-01-31 0.011565
2019-02-28 -0.185584
2019-03-31 -0.323621
2019-04-30 0.043687
Freq: M, dtype: float64
ts.resample('M',kind='period').mean()
输出:
2019-01 0.011565
2019-02 -0.185584
2019-03 -0.323621
2019-04 0.043687
Freq: M, dtype: float64
rng = pd.date_range('2019/01/01',periods = 12,freq='T')
ts = pd.Series(np.random.randn(len(rng)),index=rng)
ts.resample('5min').sum()
输出:
2019-01-01 00:00:00 1.625143
2019-01-01 00:05:00 2.588045
2019-01-01 00:10:00 2.447725
Freq: 5T, dtype: float64
金融领域中有种时间序列聚合方式,称为OHLC重采样,即计算各面元的四个值:
- Open:开盘
- High:最高值
- Low:最小值
- Close:收盘
输出:
| open | high | low | close | |
|---|---|---|---|---|
| 2019-01-01 00:00:00 | -0.345952 | 1.120258 | -0.345952 | 1.120258 |
| 2019-01-01 00:05:00 | -0.106197 | 2.448439 | -1.014186 | -1.014186 |
| 2019-01-01 00:10:00 | 1.445036 | 1.445036 | 1.002688 | 1.002688 |
另一种降采样的办法是实用pandas的groupby方法。
rng = pd.date_range('2019/1/1',periods = 100,freq='D')
ts = pd.Series(np.arange(len(rng)), index = rng)
ts.resample('m').mean()
输出:
2019-01-31 15.0
2019-02-28 44.5
2019-03-31 74.0
2019-04-30 94.5
Freq: M, dtype: float64
ts.groupby(lambda x:x.month).mean()
输出:
1 15.0
2 44.5
3 74.0
4 94.5
dtype: float64
4. 时间序列可视化
需要加载stock.csv文件,该文件格式如下:
| AA | AAPL | GE | IBM | JNJ | MSFT | PEP | SPX | XOM | |
|---|---|---|---|---|---|---|---|---|---|
| 1990/2/1 0:00 | 4.98 | 7.86 | 2.87 | 16.79 | 4.27 | 0.51 | 6.04 | 328.79 | 6.12 |
| 1990/2/2 0:00 | 5.04 | 8 | 2.87 | 16.89 | 4.37 | 0.51 | 6.09 | 330.92 | 6.24 |
| 1990/2/5 0:00 | 5.07 | 8.18 | 2.87 | 17.32 | 4.34 | 0.51 | 6.05 | 331.85 | 6.25 |
| 1990/2/6 0:00 | 5.01 | 8.12 | 2.88 | 17.56 | 4.32 | 0.51 | 6.15 | 329.66 | 6.23 |
| 1990/2/7 0:00 | 5.04 | 7.77 | 2.91 | 17.93 | 4.38 | 0.51 | 6.17 | 333.75 | 6.33 |
close_px_all = pd.read_csv('datasets/stock.csv',parse_dates = True, index_col=0)
close_px = close_px_all[['AAPL','MSFT','XOM']]
close_px.plot() #'AAPL','MSFT','XOM'股价变化

close_px.resample('B').ffill().plot() #填充工作日后,股价变化

close_px.AAPL.loc['2011-01':'2011-03'].plot() #苹果公司2011年1月到3月每日股价

close_px.AAPL.loc['2011-01':'2011-03'].plot() #苹果公司2011年1月到3月每日股价

5. 窗口函数
5.1 移动窗口函数
移动窗口函数(moving window function)指在移动窗口(可带指数衰减权数)上计算的各种统计函数,也包括窗口不定长的函数(如指数加权移动平均)。 与其他统计函数一样,移动窗口函数会自动排除缺失值。
close_px.AAPL.plot()
close_px.AAPL.rolling(250).mean().plot() #250日均线

close_px.rolling(250).mean().plot(logy=True) #250日均线 对数坐标

close_px.AAPL.rolling(250,min_periods=10).std().plot() #标准差

5.2 指数加权函数
指数加权函数:定义一个衰减因子(decay factor),以赋予近期的观测值拥有更大的权重。衰减因子常用时间间隔(span),可以使结果兼容于窗口大小等于时间间隔的简单移动窗口(simple moving window)函数。
appl_px = close_px.AAPL['2005':'2009']
ma60 = appl_px.rolling(60,min_periods=50).mean() #60日移动平均
ewma60 = appl_px.ewm(span = 60).mean() #60日指数加权移动平均
appl_px.plot()
ma60.plot(c='g',style='k--')
ewma60.plot(c='r',style='k--') #相对于普通移动平均,能“适应”更快的变化

5.3 二元移动窗口函数
相关系数和协方差等统计运算需要在两个时间序列上执行,如某只股票对某个参考指数(如标普500)的相关系数。
aapl_rets = close_px_all.AAPL['1992':].pct_change()
spx_rets = close_px_all.SPX.pct_change()
corr = aapl_rets.rolling(125,min_periods=100).corr(spx_rets) #APPL6个月回报与标准普尔500指数的相关系数
corr.plot()

all_rets = close_px_all[['AAPL','MSFT','XOM']]['2003':].pct_change()
corr = all_rets.rolling(125,min_periods=100).corr(spx_rets) #3支股票月回报与标准普尔500指数的相关系数
corr.plot()

相关文章:

一文搞懂Python时间序列
Python时间序列1. datetime模块1.1 datetime对象1.2 字符串和datatime的相互转换2. 时间序列基础3. 重采样及频率转换4. 时间序列可视化5. 窗口函数5.1 移动窗口函数5.2 指数加权函数5.3 二元移动窗口函数时间序列(Time Series)是一种重要的结构化数据形…...
GeoServer发布数据进阶
GeoServer发布数据进阶 GeoServer介绍 GeoServer是用于共享地理空间数据的开源服务器。 它专为交互操作性而设计,使用开放标准发布来自任何主要空间数据源的数据。 GeoServer实现了行业标准的 OGC 协议,例如网络要素服务 (WFS)…...
Docker离线部署
Docker离线部署 目录 1、需求说明 2、下载docker安装包 3、上传docker安装包 4、解压docker安装包 5、解压的docker文件夹全部移动至/usr/bin目录 6、将docker注册为系统服务 7、重启生效 8、设置开机自启 9、查看docker版本信息 1、需求说明 大部份公司为了服务安全…...
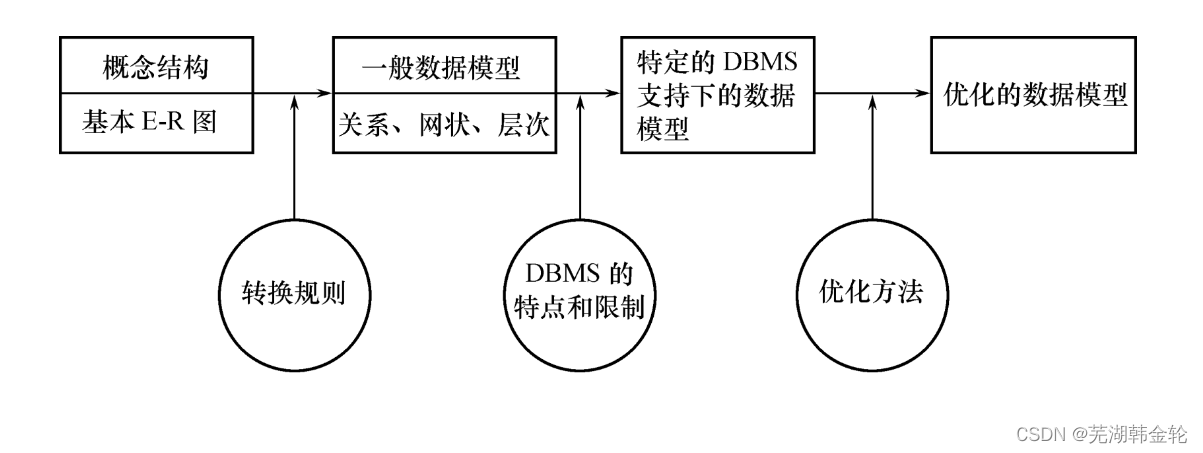
《数据库系统概论》学习笔记——第七章 数据库设计
教材为数据库系统概论第五版(王珊) 这一章概念比较多。最重点就是7.4节。 7.1 数据库设计概述 数据库设计定义: 数据库设计是指对于一个给定的应用环境,构造(设计)优化的数据库逻辑模式和物理结构&#x…...

【Datawhale图机器学习】半监督节点分类:标签传播和消息传递
半监督节点分类:标签传播和消息传递 半监督节点分类问题的常见解决方法: 特征工程图嵌入表示学习标签传播图神经网络 基于“物以类聚,人以群分”的Homophily假设,讲解了Label Propagation、Relational Classificationÿ…...
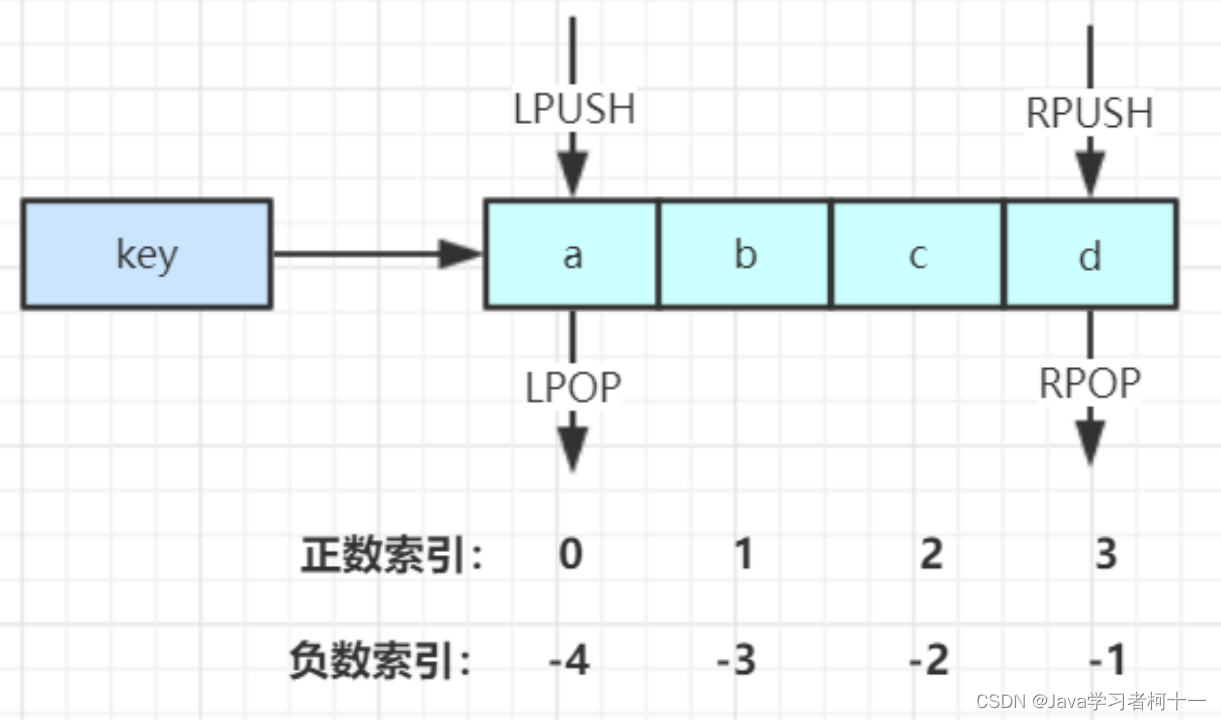
【分布式缓存学习篇】Redis数据结构
一、Redis的数据结构 二、String 数据结构 2.1 字符串常用操作 //存入字符串键值对 SET key value //批量存储字符串键值对 MSET key value [key value ...] //存入一个不存在的字符串键值对 SETNX key value //获取一个字符串键值 GET ke…...

【跟着ChatGPT学深度学习】ChatGPT带我入门NLP
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

RGB888与RGB565颜色
颜色名称RGB888原色RGB565还原色英RGB888[Hex]RGB888_R[Hex]RGB888_G[Hex]RGB888_B[Hex]RGB565[Hex]RGB565_R[Hex]RGB565_G[Hex]RGB565_B[Hex]黑色Black0x0000000000000x0000000昏灰Dimgray0x6969696969690x6B4DD1AD灰色Gray0x8080808080800x8410102010暗灰Dark Gray0xA9A9A9A9…...

常见的域名后缀有哪些?不同域名后缀的含义是什么?
域名发展至今,已演变出各种各样的域名后缀,导致很多网站管理人员在注册域名时不知该如何选择。下面,中科三方针对常见域名后缀种类,以及不同域名后缀的含义做下简单介绍。 什么是域名后缀? 域名是由一串由点分隔开的…...
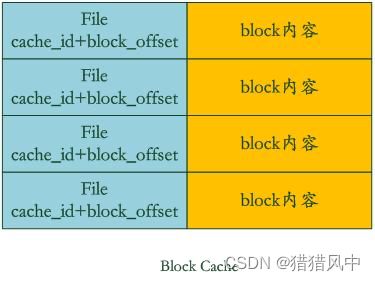
LevelDB架构介绍以及读、写和压缩流程
LevelDB 基本介绍 是一个key/value存储,key值根据用户指定的comparator排序。 特性 keys 和 values 是任意的字节数组。数据按 key 值排序存储。调用者可以提供一个自定义的比较函数来重写排序顺序。提供基本的 Put(key,value),Get(key),…...

华为OD机试模拟题 用 C++ 实现 - 快递货车(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明快递货车题目输入输出示例一输入输出Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单…...
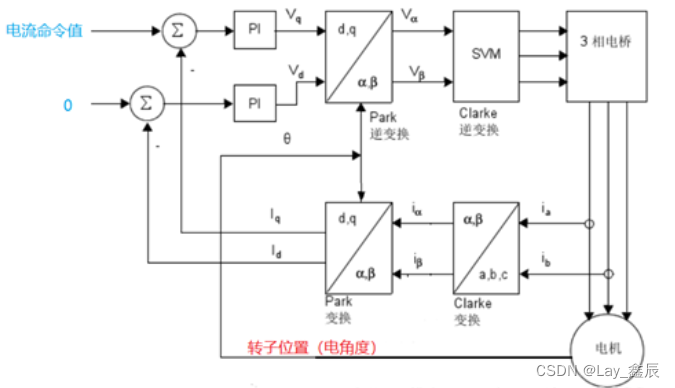
伺服三环控制深层原理解析
我们平时使用的工业伺服,通常是成套伺服,即驱动器和电机型号存在配对关系。 但有些时候,我们要用电机定转子和编码器制作非成套电机,这种时候,我们需要对驱动器进行各种设置才能驱动电机。 此篇文章将通过介绍伺服控制的三环控制原理入手来说明我们调试非成套伺服时需要…...
)
Cornerstone完整的基于 Web 的医学成像平台(一)
1.简介 Cornerstone是一个开源的基于Web的医学成像平台,它提供了一个易于使用的界面,可以用于加载、显示和处理医学图像。Cornerstone可以用于许多医学图像处理应用程序,例如计算机断层扫描(CT)、磁共振成像ÿ…...
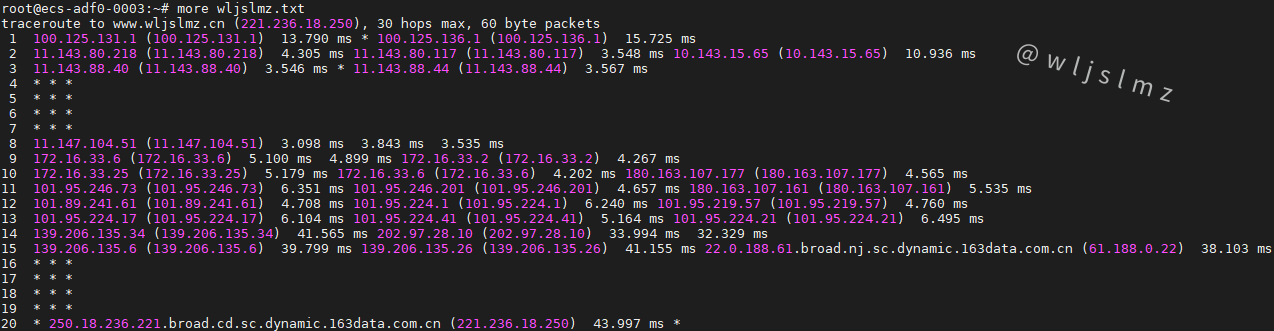
老板让我在Linux中使用traceroute排查服务器网络问题,幸好我收藏了这篇文章!
一、前言 作为网络工程师或者运维工程师,traceroute命令不会陌生,它的作用类似于ping命令,用于诊断网络的连通性,不过traceroute命令输出的命令会比ping命令丰富的多,可以跟踪从源系统到目标系统的路径。 很多工程师…...

一文读懂【数据埋点】
数据埋点是数据采集领域(尤其是用户行为数据采集领域)的术语,指的是针对特定用户行为或事件进行捕获、处理和发送的相关技术及其实施过程。比如用户某个icon点击次数、观看某个视频的时长等等。 数据分析是我们获得需求的来源之一,…...

Qt图片定时滚动播放器+透明过渡动画
目录参考结构PicturePlay.promain.cppmyqlabel.h 自定义QLabelmyqlabel.cpp自定义QLabelpictureplay.hpictureplay.cpppictureplay.uistyle.qss效果源码参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 Qt的动画类修改…...

手把手带你做一套毕业设计-征程开启
本文是《手把手带你做一套毕业设计》专栏的开篇,文本将会包含我们创作这个专栏的初衷,专栏的主体内容,以及我们专栏的后续规划。关于这套毕业设计的作者呢前端部分由狗哥负责,服务端部分则由天哥操刀。我们力求毕业生或者新手通过…...

万字解析 Linux 中 CPU 利用率是如何算出来的?
在线上服务器观察线上服务运行状态的时候,绝大多数人都是喜欢先用 top 命令看看当前系统的整体 cpu 利用率。例如,随手拿来的一台机器,top 命令显示的利用率信息如下 这个输出结果说简单也简单,说复杂也不是那么容易就能全部搞明白…...
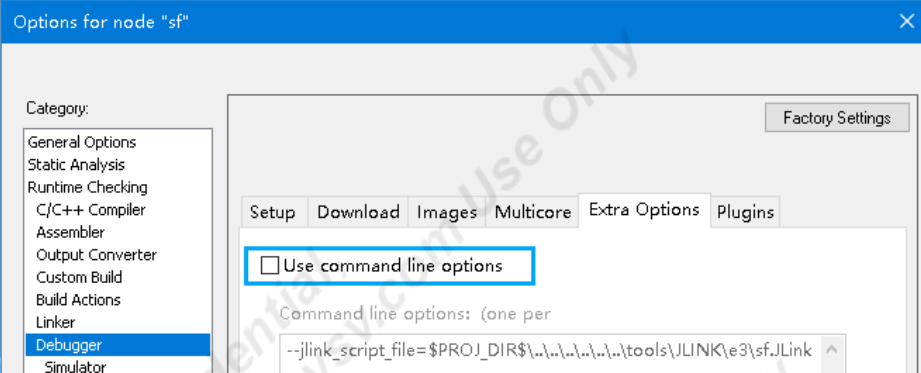
芯驰(E3-gateway)开发板环境搭建
1-Windows下环境配置 可以在Windows上使用命令行或者IAR IDE编译SSDK项目。Windows编译依赖的工具已经包含在 prebuilts/windows 目录中,包括编译器、Python和命令行工具。 1.1.1 CMD SSDK集成 msys 工具,可以在Windows命令行中完成SDK的配置、编译和…...
HiveSql一天一个小技巧:如何巧用分布函数percent_rank()求去掉最大最小值的平均薪水问题
0 问题描述参考链接(3条消息) HiveSql面试题12--如何分析去掉最大最小值的平均薪水(字节跳动)_莫叫石榴姐的博客-CSDN博客文中已经给出了三种解法,这里我们借助于此题,来研究如何用percent_rank()函数求解,简化解题思路…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
