9.2 IGMPv2
- 实验目的
(1) 熟悉IGMPv2的应用场景
(2) 掌握IGMPv2的配置方法
- 实验拓扑
实验拓扑如图9-17所示:
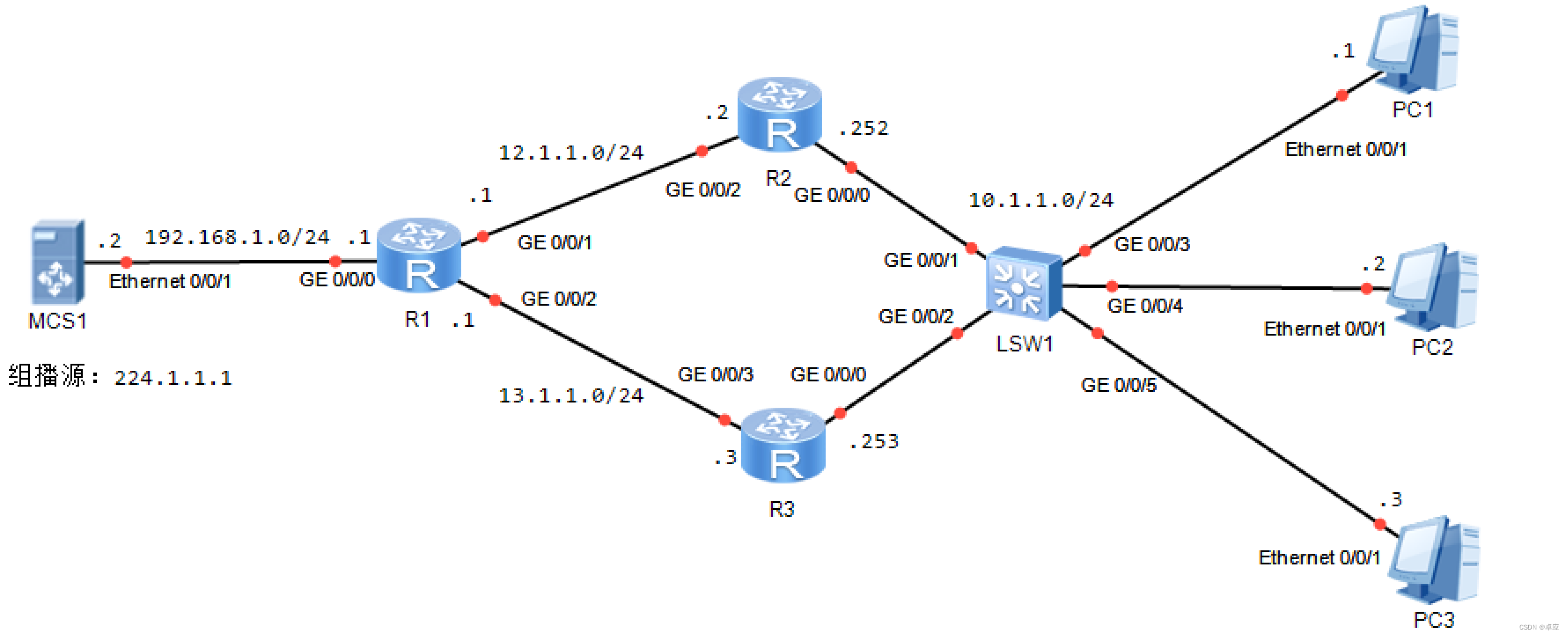
图9-17:IGMPv2
- 实验步骤
- 配置IP地址(请参考上一个实验)
- 运行IGP(请参考上一个实验)
- 运行PIM(请参考上一个实验)
- 运行IGMP V2(请参考上一个实验)
R2的配置
[R2]interface g0/0/0
[R2-GigabitEthernet0/0/0]igmp enable
[R2-GigabitEthernet0/0/0]igmp version 2
[R2-GigabitEthernet0/0/0]quit
R3的配置
[R3]interface g0/0/0
[R3-GigabitEthernet0/0/0]igmp enable
[R3-GigabitEthernet0/0/0]igmp version 2
[R3-GigabitEthernet0/0/0]quit
- 实验调试
(1)查看IGMP的接口信息
[R3]display igmp interface
Interface information of VPN-Instance: public net
GigabitEthernet0/0/0(10.1.1.253):
IGMP is enabled
Current IGMP version is 2 //版本2
IGMP state: up
IGMP group policy: none
IGMP limit: -
Value of query interval for IGMP (negotiated): -
Value of query interval for IGMP (configured): 60 s //查询间隔
Value of other querier timeout for IGMP: 97 s
Value of maximum query response time for IGMP: 10 s //最大响应定时器为10s
Querier for IGMP: 10.1.1.252 //查询器优选IP地址最小的
Total 1 IGMP Group reported
(2)打开调试信息
<R2>debugging igmp query
<R2>terminal monitor
<R2>terminal debugging
<R2>debugging igmp leave
[R2]info-center enable
(3)让PC1加入组224.1.1.1,其配置如图9-18所示:

图9-18:配置PC1加入组224.1.1.1
(4)查看调试信息
<R2>
Jun 30 2022 17:42:25.660.1-08:00 R2 IGMP/7/QUERY:(public net): Send version 2 general query on GigabitEthernet0/0/0(10.1.1.252) to destination 224.0.0.1 (G073310)
Jun 30 2022 17:42:36.600.3-08:00 R2 IGMP/7/EVENT:(public net): (S,G) creation event received for (192.168.1.2/32, 224.1.1.1/32). (G01985)
Jun 30 2022 17:42:36.600.4-08:00 R2 IGMP/7/EVENT:(public net): No state in global MRT. Not merging downstream for (192.168.1.2/32, 224.1.1.1/32) on interface GigabitEthernet0/0/2(12.1.1.2). (G011016)
(5)配置PC1离开组224.1.1.1,其配置如图9-19所示:
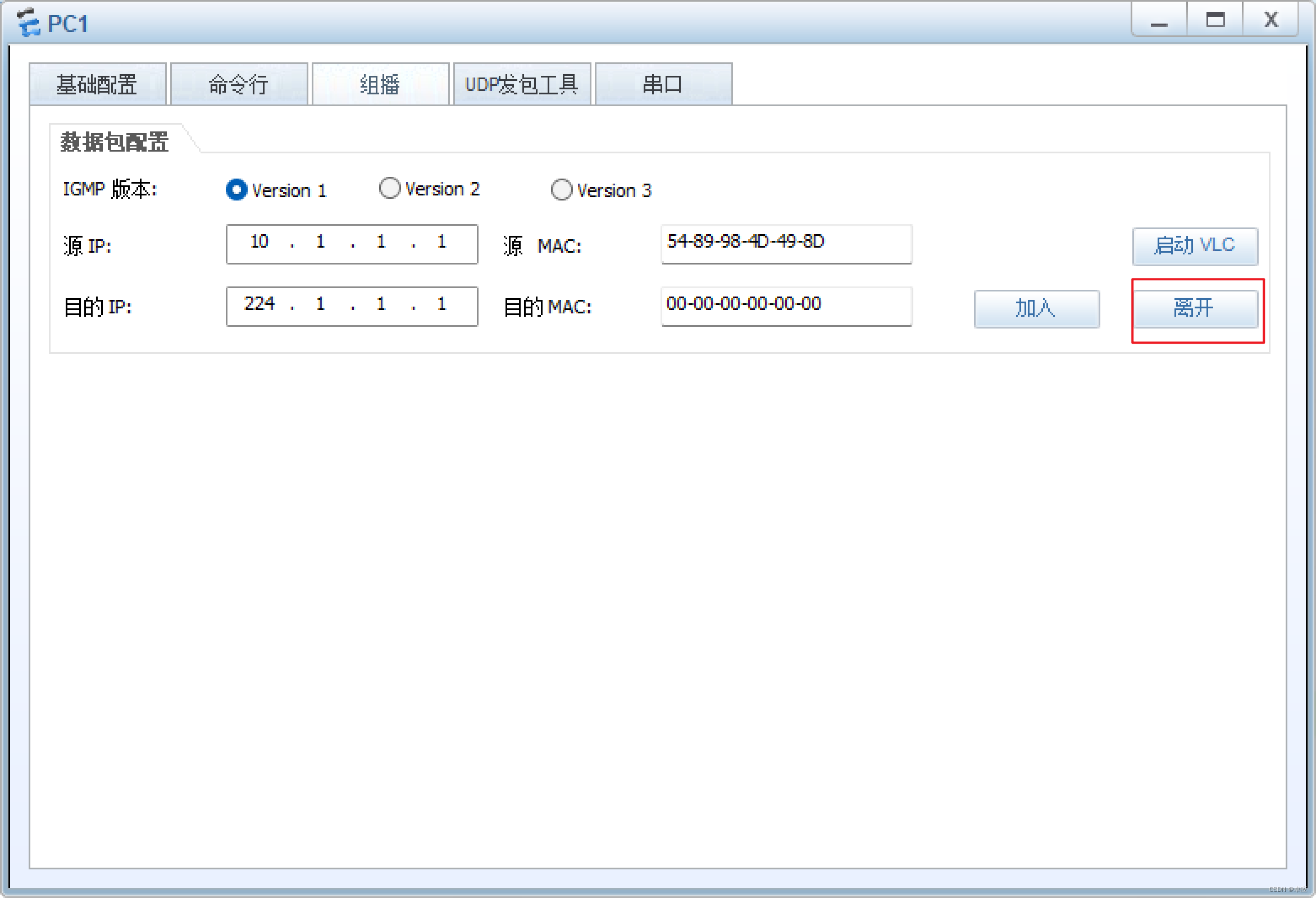
图9-19:配置PC1离开组224.1.1.1
(7)查看抓包情况
第一步:PC1发送离开组消息,离开组报文的格式如图9-20所示:
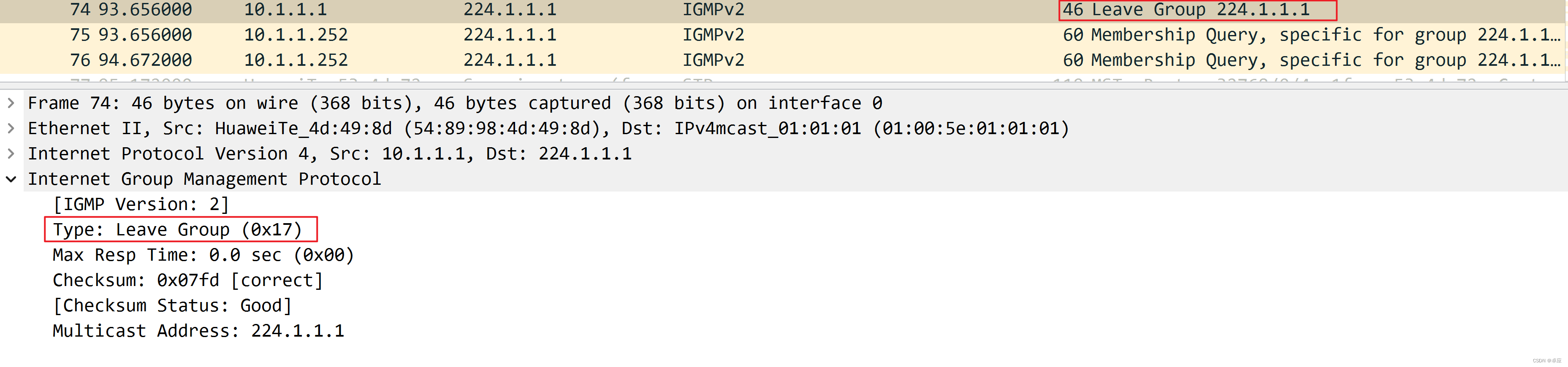
华为Datacom网络工程师HCIP全套学习课程(全套理论+实验)-学习视频教程-腾讯课堂 图9-20:离开组报文的格式
第二步:查询器会连发二个特定组查询,时间间隔为1s,其报文格式如图9-21所示:
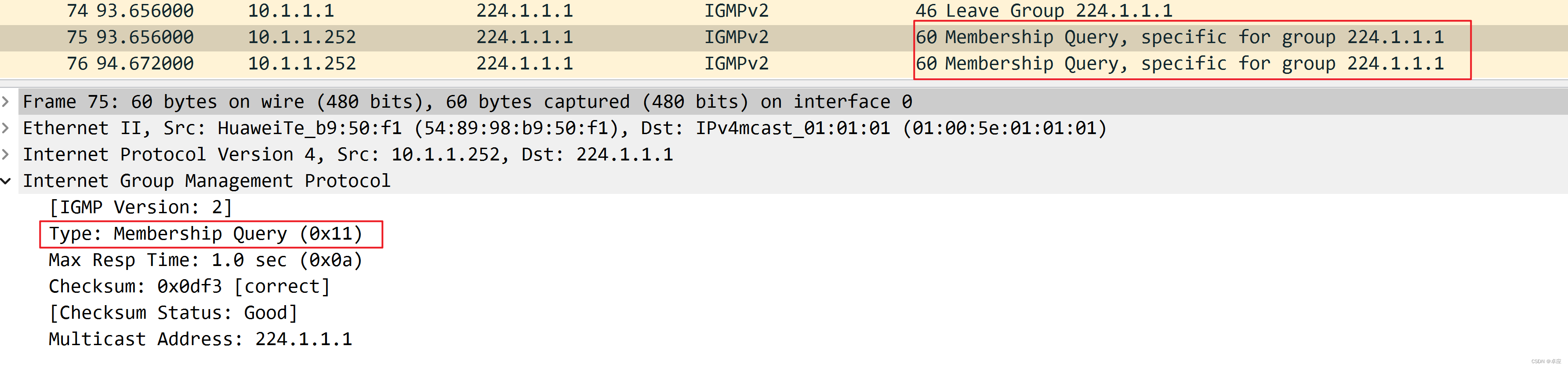
图9-21:查询报文格式
【技术要点】IGMPv2比IGMP新增加的包
1、leave
2、特定组查询
相关文章:

9.2 IGMPv2
实验目的 (1) 熟悉IGMPv2的应用场景 (2) 掌握IGMPv2的配置方法 实验拓扑 实验拓扑如图9-17所示: 图9-17:IGMPv2 实验步骤 配置IP地址(请参考上一个实验)运行IGPÿ…...
巨头混战,抢着“兜底”自动驾驶安全
诚然,中国汽车行业的发展绝对不会拘泥于电动化,必定会在电动化的基础上,迎接下半场的快速智能化。 2021年6月,长城汽车线控底盘全球首次发布。 彼时,长城汽车技术副总裁宋东先宣布,整合了线控转向、线控制…...

RightCapital 第一轮面试题
现在我们就马上开始吧! 答案在文末 JavaScript 是一门单线程的静态类型语言(单选题) 正确 错误 在 JavaScript 中下面哪种类型的值是不可变的(immutable)(单选题) Object Symbol Array Date …...
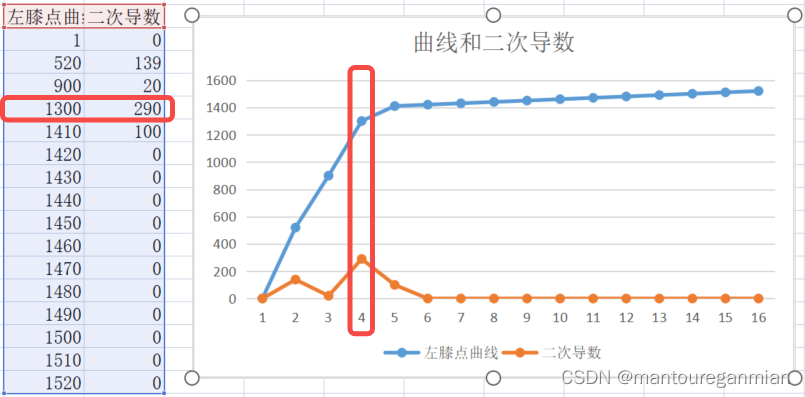
Python曲线肘部点检测-膝部点自动检测
文章目录一. 术语解释二. 拐点检测肘部法则是经常使用的法则。很多时候,可以凭人工经验去找最优拐点,但有时需要自动寻找拐点。最近解决了一下这个问题,希望对各位有用。一. 术语解释 **肘形曲线(elbow curve)**类似人胳膊状的曲线ÿ…...
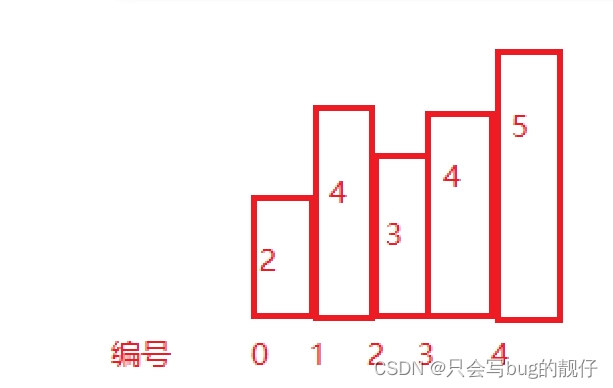
【算法题】最大矩形面积,单调栈解法
力扣:84. 柱状图中最大的矩形 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 题意很简单,翻译一下就是:求该图中…...

活动策划|深度分析年货节活动该如何策划!
四月初,不平凡的初春开始恢复往日的平静。对于新零售行业,疫情的缓解也逐渐平稳生态链的运转。2020年新零售的格局在洗礼后,业务的聚焦点也从前端促销转移到后端履约的体验闭环,同时很大程度的推进企业在危机公关下的应对。618大促…...

Idea启动遇到 Web server failed to start. Port 8080 was already in use. 报错
Idea启动遇到问题-记录 报错英文提示: APPLICATION FAILED TO START Description: Web server failed to start. Port 8080 was already in use. Action: Identify and stop the process that’s listening on port 8080 or configure this application to liste…...
函数知识点总结)
Python3中zip()函数知识点总结
1.引言 在本文中,我将带领大家深入了解Python中的zip()函数,使用它可以提升大家的工作效率。 闲话少说,我们直接开始吧! 2. 基础知识 首先,我们来介绍一些基础知识点: Python中的某些数据类型是不可变的…...

过滤器,监听器,拦截器的原理与在Servlet和Spring的应用
在Java Web的开发中,最原始和初期的学习都是从Servlet开始的,Servlet是Java最为耀眼的技术,也是Java EE的技术变革。目前大火主流的框架spring boot也的spring mvc部分也是基于拓展servlet完成的。回到之前的文章spring 实现了对servlet的封装…...

minio spring boot 秒传、分片上传、断点续传文件实现
此处后端使用的是前期封装的自定义starter,具体链接可参考:minio对象存储spring boot starter封装组件 这里主要针对前期封装的组件,做一个简单的应用,前端直传可查看之前的文章 秒传 秒传的逻辑比较简单,在前传上传…...

MTK平台使用Omnipeek分析空口协议讲解
讲解这个之前,我们先来了解下beacon/robe Request/Probe Response 三种帧 beacon帧 信标帧,由AP以一定的时间间隔周期性发出,以此来告诉外界自己无线网络的存在。 Beacon帧作为802.11中一个周期性的帧,Beacon周期调高,对应睡眠周期拉长,故节能(即越来休息100ms再起来…...
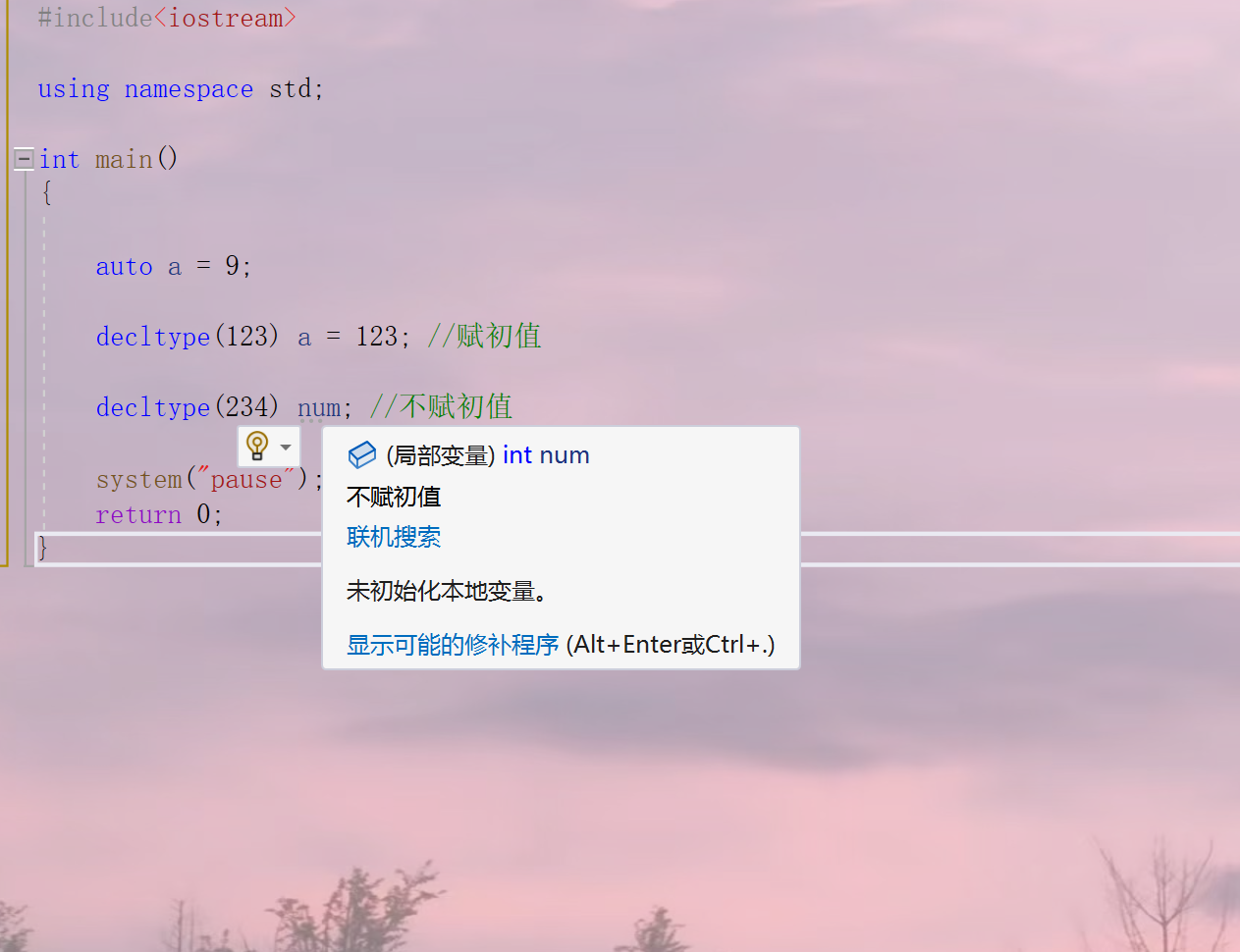
string和自动推断类型
欢迎来观看温柔了岁月.c的博客目前设有C学习专栏C语言项目专栏数据结构与算法专栏目前主要更新C学习专栏,C语言项目专栏不定时更新待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏一周主要三更,星期三,星期五,星…...
【软件测试】从功能到自动化测试,测试人的进阶之路细节,这些必不可少......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 测试流程࿰…...
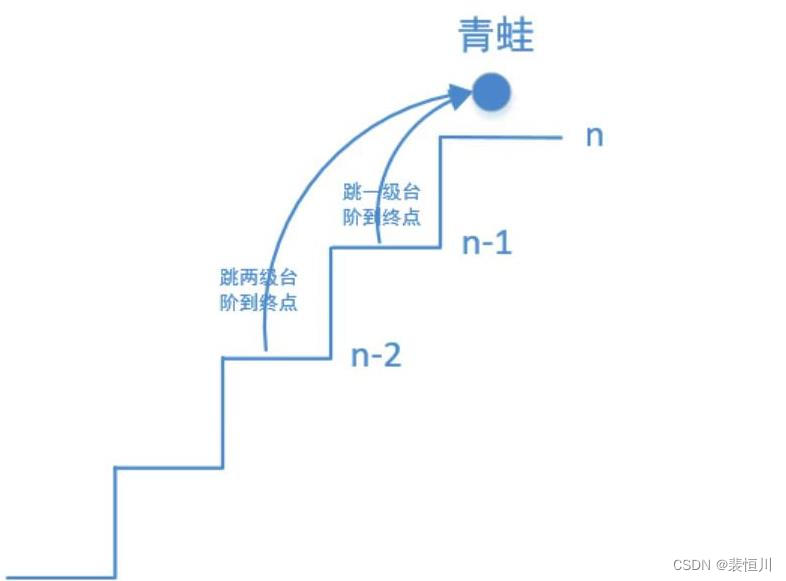
C语言青蛙跳台阶【图文详解】
青蛙跳台阶前言1. 题目介绍2. 解题思路3. 利用图片来演示青蛙跳台阶的原理4. 如何用C语言实现青蛙跳台阶前言 在本文,我们要与一只活泼可爱的小青蛙合作,带领着它跳上台阶,这个小家伙精力充沛,特别擅长于跳跃。我们要让它做我们的…...
——list容器的基础理论知识)
笔记(五)——list容器的基础理论知识
list容器是一个双向链表容器,可以高效地进行插入删除元素,但是不能随机存取元素(不支持at()和[]操作符)。一、list容器的对象构造方法list对象采用模板类的默认构造形式例如list<T> lst;#include<iostream>…...

浅谈网络中接口幂等性设计问题
所谓幂等性设计,就是说,一次和多次请求某一个资源应该具有同样的副作用。用数学的语言来表达就是:f(x) f(f(x))。 在数学里,幂等有两种主要的定义。 在某二元运算下,幂等元素是指被自己重复运算(或对于函数…...
《C Primer Plus》第13章复习题与编程练习
《C Primer Plus》第13章复习题与编程练习复习题1. 下面的程序有什么问题?2. 下面的程序完成什么任务?(假设在命令行环境中运行)3. 假设程序中有下列语句:4. 编写一个程序,不接受任何命令行参数或接受一个命…...

计算机SCI论文应该怎么作图? - 易智编译EaseEditing
计算机SCI论文,作图时要注意以下几个方面的问题: 1.图片的格式要tiff或者eps; 2.文件大小不能超过10M; 3.长和宽也给出了具体要求; 4.色彩模式要RGB或者灰度图; 5.文中的文字字体和大小; …...
【一】kubernetes集群部署
一、docker环境搭建 1、移除以前docker相关包 sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-engine2、配置yam源 sudo yum install -y yum-utilssudo yum-config-manager --ad…...

Docker安装Redis
一、拉取镜像 命令::docker pull <镜像名称>:<版本号> docker pull redis 二:Docker挂载配置文件 挂载:即将宿主的文件和容器内部目录相关联,相互绑定,在宿主机内修改文件的话也随之修改容…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
