【华为OD题库-008】座位调整-Java
题目
疫情期间课堂的座位进行了特殊的调整,不能出现两个同学紧挨着,必须隔至少一个空位。给你一个整数数组desk表示当前座位的占座情况,由若干0和1组成,其中0表示没有占位,1表示占位。在不改变原有座位秩序情况下,还能安排坐几个人?
输入描述:
第一行是一个数组表示作为占座情况,由若干0和1组成,其中0表示没有占位,1表示占位
输出描述:
输出数值表示还能坐几个人
补充说明:
1 <= desk.length <= 2*10^4
示例1
输入:
1,0,0,0,1
输出:
1
说明:
只有desk[2]的位置可以坐一个人
思路
遍历,找出当前为0的位置,如果其前后均不为1,那么此位置可以坐人,将此位置标记为1,结果cnt++;遍历完成后返回cnt即可。
假设当前遍历位置为i,i的范围为[0,len-1],len为数组arr总长度。要让i的前后均不为1,即arr[i-1]!=1&&arr[i+1]!=1。考虑数组越界情况:
- 当i-1<0时(i=0),只用考虑arr[i+1]!=1
- 当i+1>=len时(i=len-1),只用考虑arr[i-1]!=1
综上,利用逻辑与短路规则,可以将上述表达式归纳为:
(i == 0 || arr[i - 1] != 1) && (i == n - 1 || arr[i + 1] != 1)
题解
package hwod;import java.util.Arrays;
import java.util.Scanner;public class SeatAjust {public static void main(String[] args) {Scanner sc = new Scanner(System.in);String[] inputs = sc.nextLine().split(",");int[] seats = Arrays.stream(inputs).mapToInt(Integer::parseInt).toArray();System.out.println(getSeatCnt(seats));}private static int getSeatCnt(int[] seats) {int n = seats.length;int cnt = 0;for (int i = 0; i < n; i++) {if (seats[i] == 0) {if ((i == 0 || seats[i - 1] != 1) && (i == n - 1 || seats[i + 1] != 1)) {seats[i] = 1;cnt++;}}}return cnt;}
}推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。
相关文章:

【华为OD题库-008】座位调整-Java
题目 疫情期间课堂的座位进行了特殊的调整,不能出现两个同学紧挨着,必须隔至少一个空位。给你一个整数数组desk表示当前座位的占座情况,由若干0和1组成,其中0表示没有占位,1表示占位。在不改变原有座位秩序情况下&…...

4 Paimon数据湖之Hive Catalog的使用
更多Paimon数据湖内容请关注:https://edu.51cto.com/course/35051.html Paimon提供了两种类型的Catalog:Filesystem Catalog和Hive Catalog。 Filesystem Catalog:会把元数据信息存储到文件系统里面。Hive Catalog:则会把元数据…...

Verilog刷题[hdlbits] :Bcdadd100
题目:Bcdadd100 You are provided with a BCD one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out. 为您提供了一个名为bcd_fadd的BCD一位数加法器,它将两个BCD数字相加并带入,并生…...
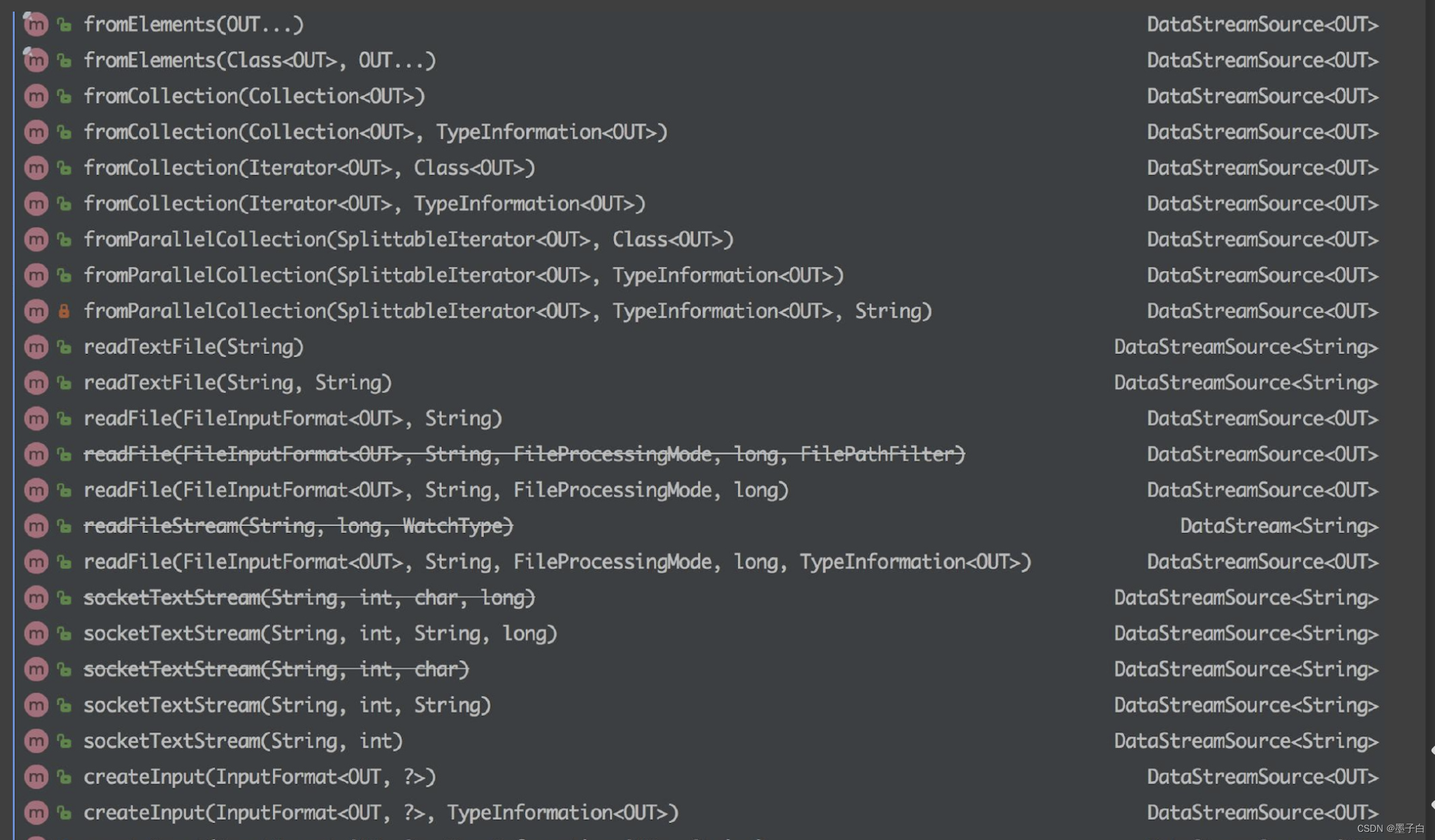
Flink—— Data Source 介绍
Data Source 简介 Flink 做为一款流式计算框架,它可用来做批处理,即处理静态的数据集、历史的数据集;也可以用来做流处理,即实时的处理些实时数据流,实时的产生数据流结果,只要数据源源不断的过来ÿ…...
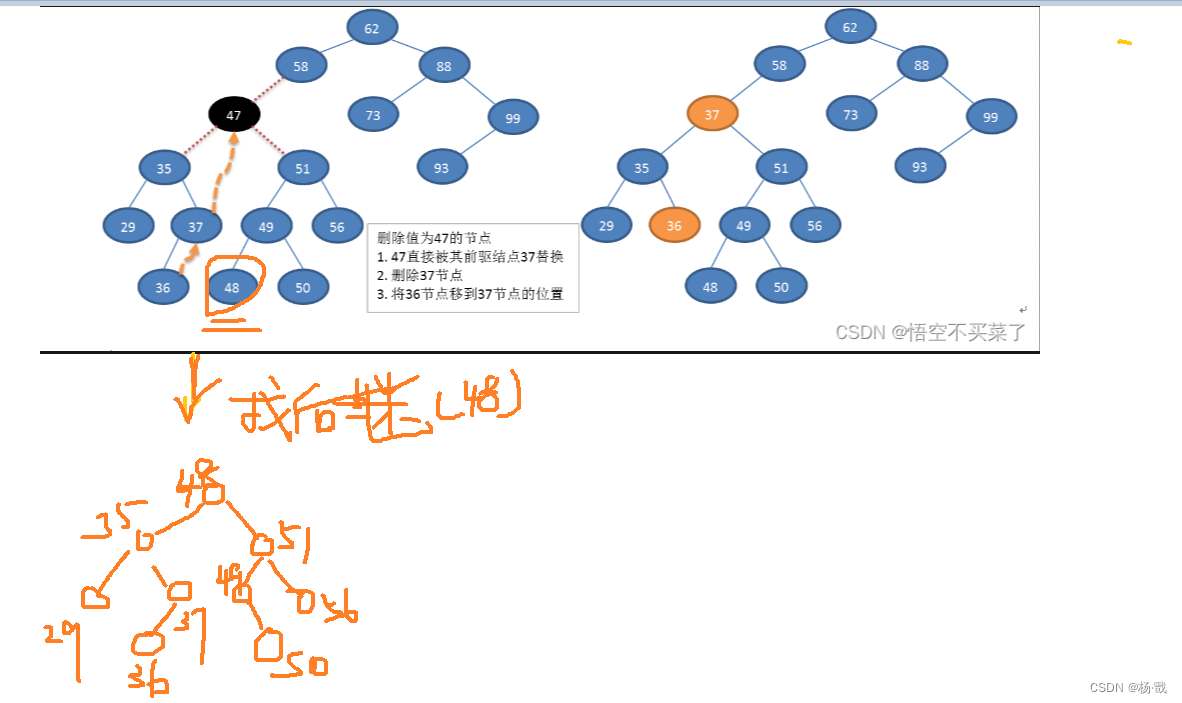
树之二叉排序树(二叉搜索树)
什么是排序树 说一下普通二叉树可不是左小右大的 插入的新节点是以叶子形式进行插入的 二叉排序树的中序遍历结果是一个升序的序列 下面是两个典型的二叉排序树 二叉排序树的操作 构造树的过程即是对无序序列进行排序的过程。 存储结构 通常采用二叉链表作为存储结构 不能 …...
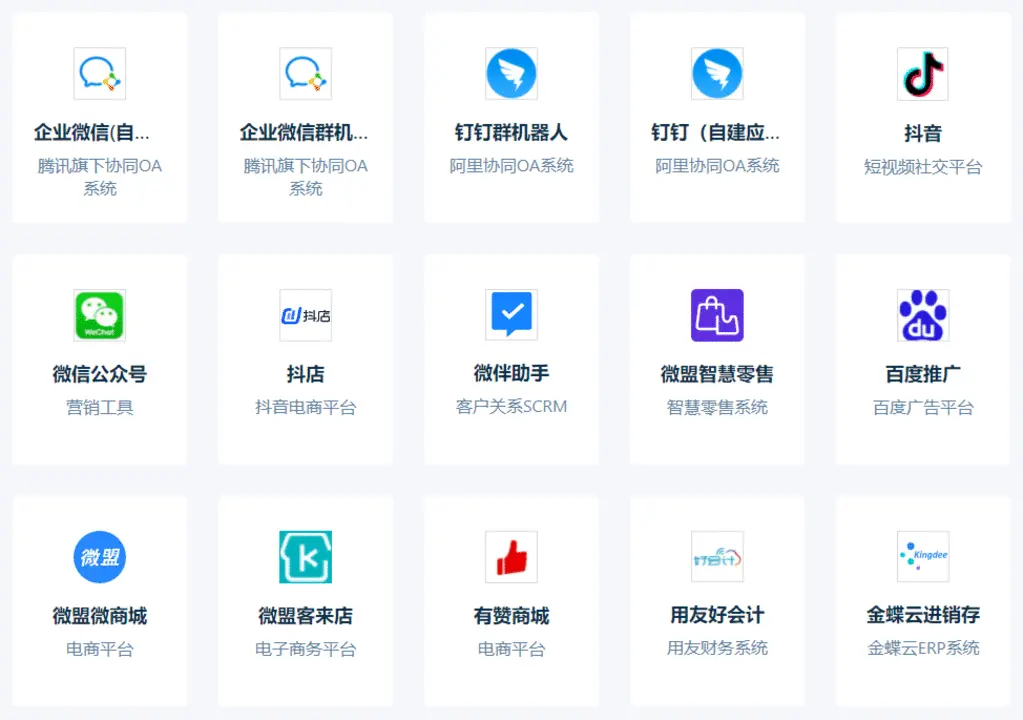
管易云与电商平台的无代码集成:实现API连接与用户运营
管易云简介及其与电商平台的合作 金蝶管易云是金蝶集团旗下以电商为核心业务的子公司,是国内最早的电商ERP服务商之一,总部在上海,与淘宝、天猫、 京东、拼多多、抖音等300多家主流电商平台建立合作关系,同时管易云是互联网平台首…...
)
ElementUI的el-upload上传组件与表单一起提交遇到的各种问题以及解决办法(超详细,每个步骤都有详细解读)
背景: 使用ruoyi-vue进行2次开发,需要实现表单与文件上传一起提交,并且文件上传有4个,且文件校验很复杂,因此ruoyi-vue集成的上传组件FileUpload调试几天后发现真不太适用,最终选择element UI原生组件el-upload(FileUpload也是基于el-upload实现的),要实现表单与文件同…...

python flask_restful “message“: “Failed to decode JSON object: None“
1、问题表现 "message": "Failed to decode JSON object: None"2、出现的原因 Werkzeug 版本过高 3、解决方案 pip install Werkzeug2.0解决效果 可以正常显示json数据了 {"message": {"rate": "参数错误"} }...
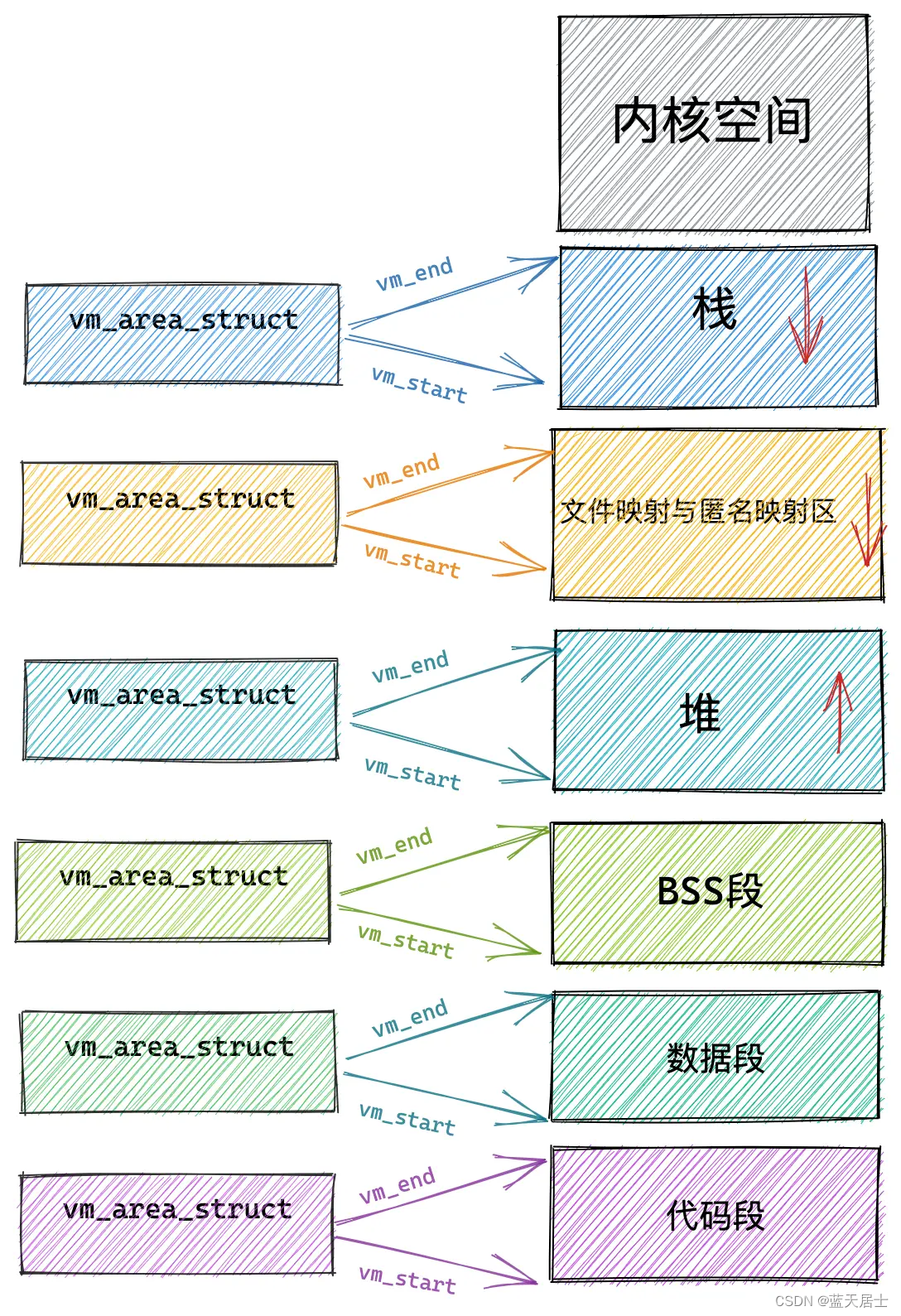
Linux内核有什么之内存管理子系统有什么第六回 —— 小内存分配(4)
接前一篇文章:Linux内核有什么之内存管理子系统有什么第五回 —— 小内存分配(3) 本文内容参考: linux进程虚拟地址空间 《趣谈Linux操作系统 核心原理篇:第四部分 内存管理—— 刘超》 特此致谢! 二、小…...
)
【OpenHarmony内核】Harmony内核之线程操作函数(二)
文章目录 前言一、获取线程优先级二、转交控制运行权三、挂起线程3.1 线程的挂起是什么意思?3.2 函数介绍四、恢复线程五、分离指定的线程5.1 分离线程是什么意思5.2 函数介绍六、等待线程终止运行七、终止当前线程的运行八、终止指定线程的运行九、获取活跃线程数总结前言 O…...

二十五、W5100S/W5500+RP2040树莓派Pico<Modebus TCP Server示例>
文章目录 1 前言2 简介2 .1 什么是Modbus TCP?2.2 Modbus TCP指令介绍2.3 请求数据过程2.4 Modbus TCP协议优点2.5 Modbus TCP应用场景 3 WIZnet以太网芯片4 Modbus TCP示例概述以及使用4.1 流程图4.2 准备工作核心4.3 连接方式4.4 主要代码概述4.5 结果演示 5 注意…...

Android画个圆点状态灯
1、创建一个 XML 文件在 res/drawable 目录下(默认为黑色) <?xml version"1.0" encoding"utf-8"?> <shape xmlns:android"http://schemas.android.com/apk/res/android"android:shape"oval"><…...

高性能网络编程 - 解读3种线程模型
文章目录 Pre线程模型1:传统阻塞 I/O 服务模型线程模型2:Reactor 模式Reactor 模式的基本设计思想Reactor 模式中的关键组成3种典型实现单 Reactor 单线程单 Reactor 多线程主从 Reactor 多线程 小结 线程模型3:Proactor 模型 Pre 高性能网络…...
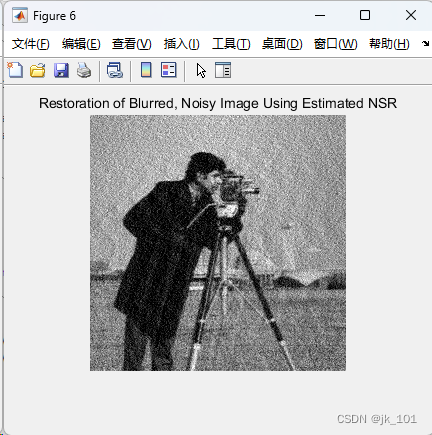
MATLAB中deconvwnr函数用法
目录 语法 说明 示例 使用 Wiener 滤波对图像进行去模糊处理 deconvwnr函数的功能是使用 Wiener 滤波对图像进行去模糊处理。 语法 J deconvwnr(I,psf,nsr) J deconvwnr(I,psf,ncorr,icorr) J deconvwnr(I,psf) 说明 J deconvwnr(I,psf,nsr) 使用 Wiener 滤波算法对…...

赛宁网安入选国家工业信息安全漏洞库(CICSVD)2023年度技术组成员单
近日,由国家工业信息安全发展研究中心、工业信息安全产业发展联盟主办的“2023工业信息安全大会”在北京成功举行。 会上,国家工业信息安全发展研究中心对为国家工业信息安全漏洞库(CICSVD)提供技术支持的单位授牌表彰。北京赛宁…...

Git系列之Git集成开发工具及git扩展使用
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是君易--鑨,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的博客专栏《Git实战开发》。🎯🎯 &a…...

selenium headless 无头模式慢
selenium设置headlessTrue发现非常慢,headlessFalse要快很多。 最后测试发现升级到selenium最新版本,selenium4.15.2。设置--headlessnew,解决了,速度正常了。 新版selenium有了两种headless模式,参见:He…...
快速修复因相机断电导致视频文件打不开的问题
3-5 本文主要解决因相机突然断电导致拍摄的视频文件打不开的问题。 在日常工作中,有时候需要使用相机拍摄视频,比如现在有不少短视频拍摄的需求,如果因电池突然断电的原因,导致拍出来的视频播放不了,这时候就容易出大…...

Ceph 笔记, ssh写入缓存
硬件建议 — Ceph 文档 写入缓存 企业级 SSD 和 HDD 通常包括断电保护功能,包括 在运行时断电时确保数据耐久性,以及 使用多级缓存来加快直接或同步写入速度。这些设备 可以在两种缓存模式之间切换 -- 刷新到的易失性缓存 具有 fsync 的持久性媒体&a…...
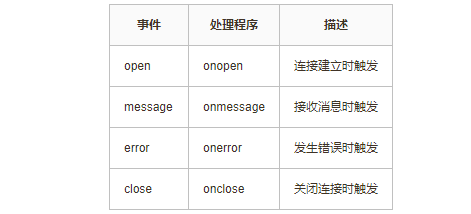
WebSocket魔法师:打造实时应用的无限可能
1、背景 在开发一些前端页面的时候,总是能接收到这样的需求:如何保持页面并实现自动更新数据呢?以往的常规做法,是前端使用定时轮询后端接口,获取响应后重新渲染前端页面,这种做法虽然能达到类似的效果&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
