数据结构与算法C语言版学习笔记(6)-树、二叉树、赫夫曼树
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、树的定义
- 1.结点的度、树的度
- 2.结点的逻辑关系
- 3.树的深度
- 4.有序树和无序树
- 5.森林
- 二、树的存储结构
- (1)双亲表示法
- (2)孩子表示法
- ①每个结点的指针域数量等于整个树的度
- ②每个结点的指针域数量等于自己的度
- ③升级改进后的孩子表示法
- (3)孩子兄弟表示法
- 三、二叉树
- 1.背景引出
- 2.二叉树的特殊形态
- (1)斜树
- (2)满二叉树
- (3)完全二叉树
- 3.二叉树的性质
- 4.二叉树的存储结构
- 5.二叉树的遍历算法(前序、中序、后序)
- ①前序遍历
- ②中序遍历:
- ③后序遍历:
- 6.已知前序/中序/后序三者中的其二,求另外一个
- 7.建立一颗二叉树
- 六、线索二叉树
- 七、赫夫曼树
前言
前面说,数据的逻辑结构包括线性结构和非线性结构,线性结构学了线性表(顺序表与链表)、栈与队列、串等,而现在要接触的树是非线性结构,它是一对多的关系,更加复杂。
一、树的定义
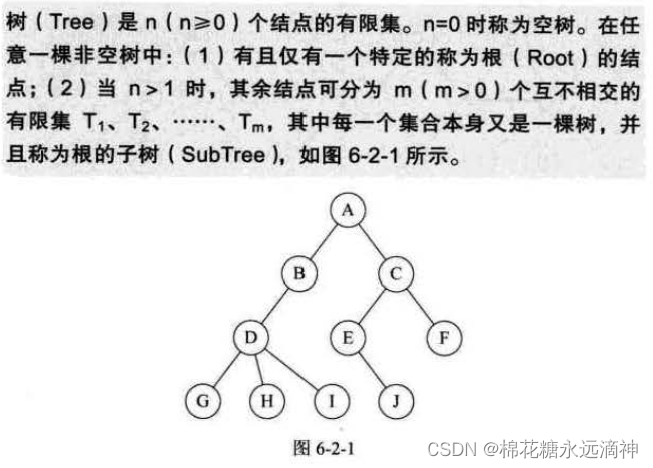
1.结点的度、树的度
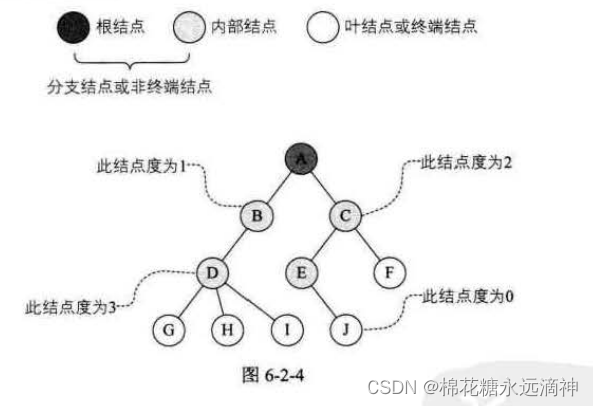
(1)结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶结点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。比如D有三个子树,度为3;C有两个子树,度为2。
(2)树的度是树内各结点的度的最大值。如图6-2-4所示,因为这棵树结点的度的最大值是结点D的度,为3,所以树的度也为3。
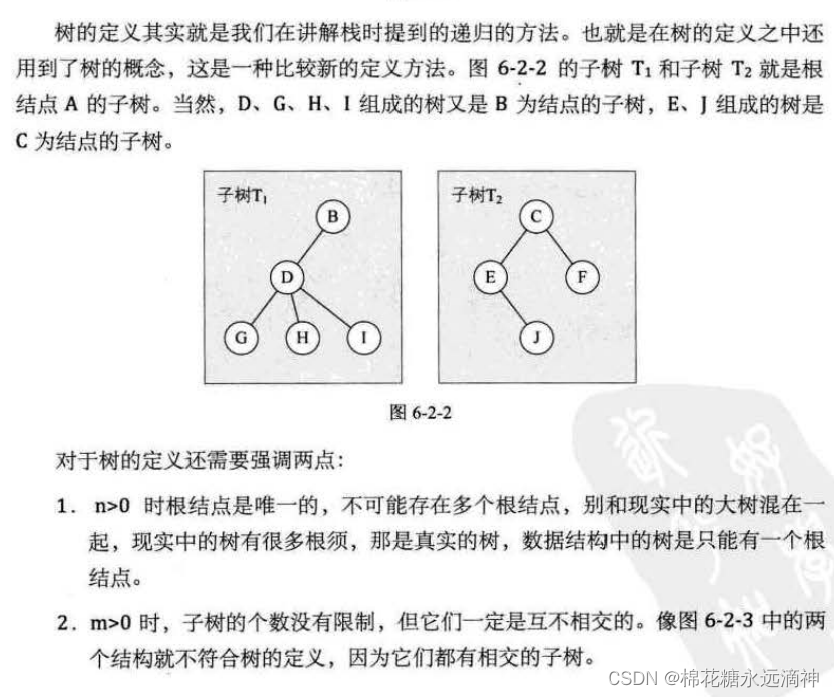
2.结点的逻辑关系
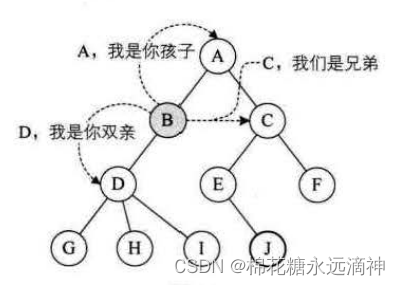
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。嗯,为什么不是父或母,叫双亲呢?对于结点来说其父母同体,唯一的一个,所以只能把它称为双亲了。同一个双亲的孩子之间互称兄弟(Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。所以对于H来说,D、B、A 都是它的祖先。反之,以某结点为根的子树中的任一结点都称为该结点的子孙。
3.树的深度
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。若某结点在第1层,则其子树的根就在第l+1层。其双亲在同一层的结点互为堂兄弟。显然图6-2-6中的D、E、F是堂兄弟,而G、H、1、J也是。树中结点的最大层次称为树的深度(Depth)或高度,当前树的深度为4。
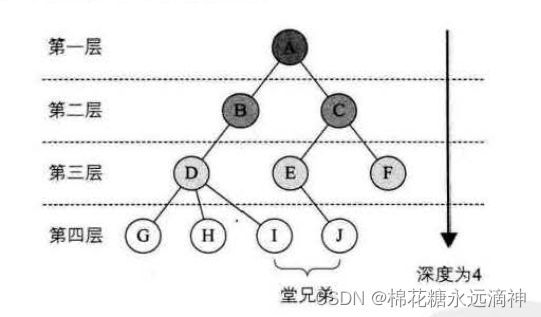
4.有序树和无序树
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树
5.森林

二、树的存储结构
树的存储结构不同于线性表,由于结构的差异,很难用顺序结构来表示,这里产生了针对树的三种存储结构:
(1)双亲表示法:每个节点除了数据域外,还包含一个指向父节点的指针。根节点的指针为空。这种存储结构方便查找父节点,但是查找子节点需要遍历整个树。
(2)孩子表示法:每个节点包含一个指向第一个子节点的指针,以及一个指向兄弟节点的指针。这种存储结构方便查找子节点和兄弟节点,但是查找父节点需要遍历整个树。
(2)孩子兄弟表示法:每个节点包含一个指向第一个子节点的指针,以及一个指向下一个兄弟节点的指针。这种存储结构比较灵活,可以表示任意树形结构,但是查找父节点需要遍历整个树。
(1)双亲表示法
我们人可能因为种种原因,没有孩子,但无论是谁都不可能是从石头里出来的,所以是人一定会有父母。树这种结构也不例外,除了根结点外,其余每个结点,它不一定有孩子,但是一定有且仅有一个双亲。
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。也就是说,每个结点除了知道自己是谁以外,还知道它的双亲在哪里。它的结点结构为表6-4-1所示。

其中 data是数据域,存储结点的数据信息。而 parent是指针域,存储该结点的双亲在数组中的下标。所以它与链表还是有区别的,链表指针域存储的是后驱结点的地址。
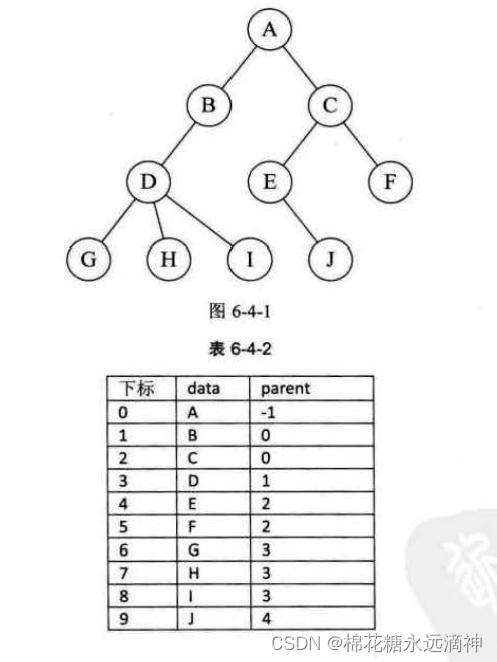
所以我们可以通过一个结点很容易找到其双亲结点,但是很难找到其孩子节点。
如果需要解决找到孩子结点的问题,当然可以再拓展一个指针域,用来存储一个长子的位置。
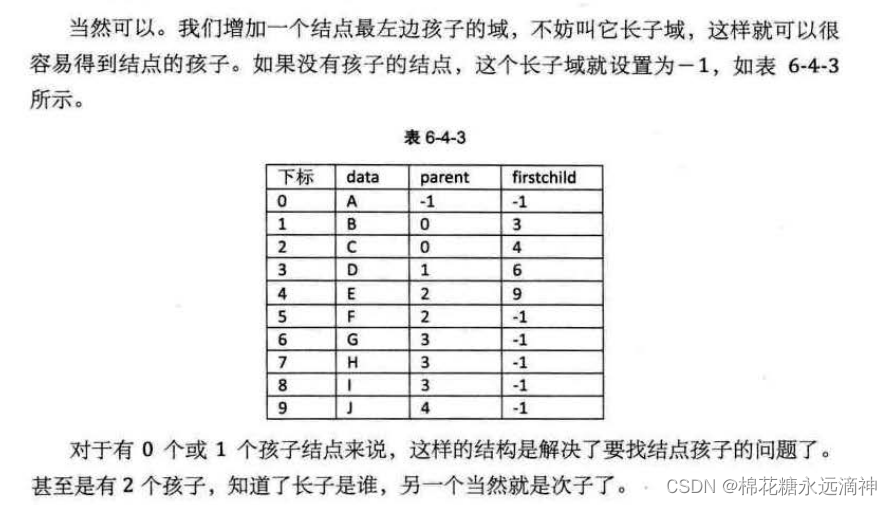
(2)孩子表示法
顾名思义,每一个结点除了自己的数据域外,指针域存储了自己的孩子结点的位置。
①每个结点的指针域数量等于整个树的度
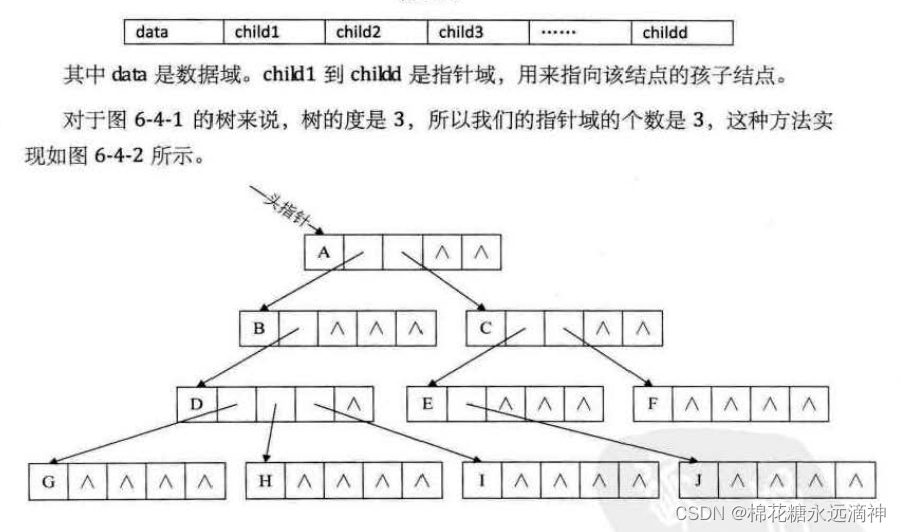
很明显,最大的缺点就是每个结点的子节点个数不一致,所以会空出许多空间没有被利用,浪费存储空间。
②每个结点的指针域数量等于自己的度
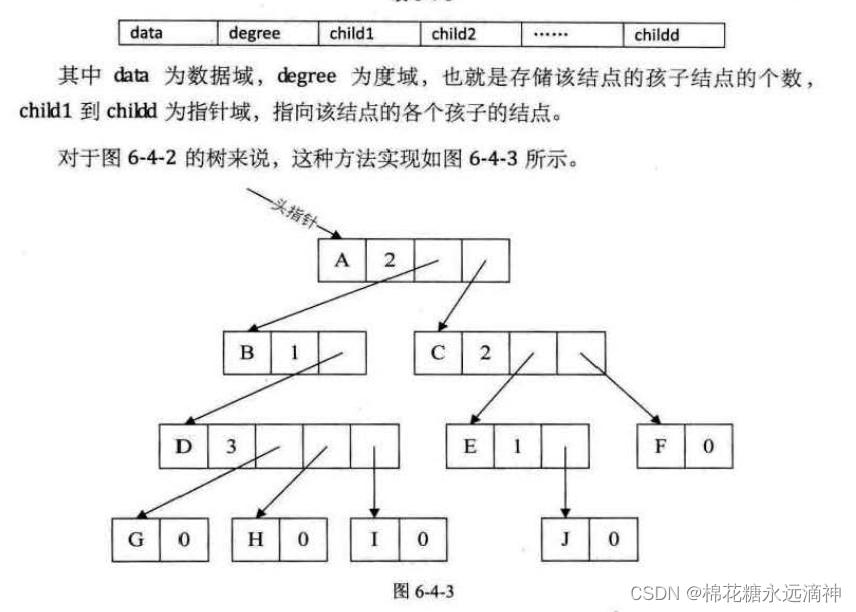
这也有缺点,每个结点的存储结构不同,看着很费劲。
③升级改进后的孩子表示法
为了既可以节省存储空间,又可以将存储结构看起来整齐划一,设计了升级版的孩子表示法:
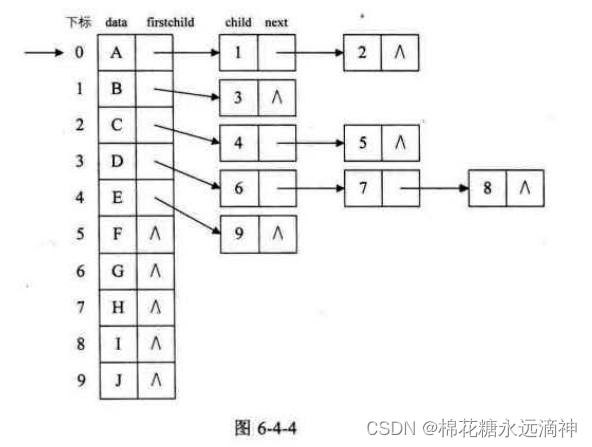
如图,对于一棵树,变成了顺序表+链表的形式,每个结点的数据和长子指针构成了一个顺序结构的一维数组,然后每个节点的长子结点又引出链式结构,指向第二个孩子,第二个孩子结点又有一个next指针指向后驱结点即第三个孩子,如此往复。
孩子表示法结构体:


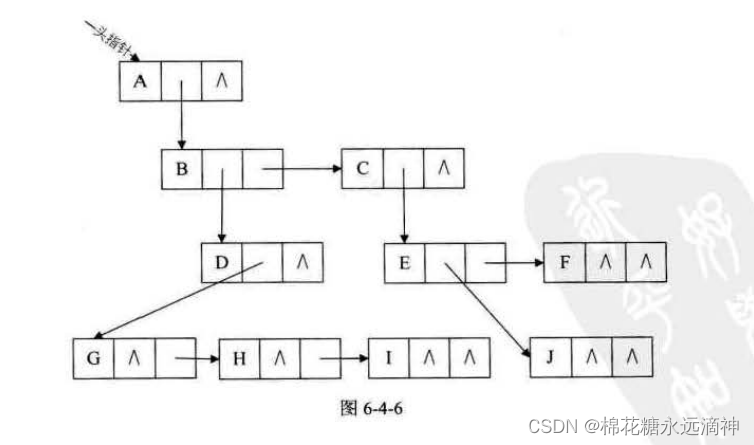
(3)孩子兄弟表示法
刚才我们分别从双亲的角度和从孩子的角度研究树的存储结构,如果我们从树结点的兄弟的角度又会如何呢?当然,对于树这样的层级结构来说,只研究结点的兄弟是不行的,我们观察后发现,任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。

简而言之,一个结点的数据域是自己的数据,两个指针域,第一个指向自己的长子,第二个指向自己的右边的兄弟。
三、二叉树
1.背景引出
我们玩猜数字游戏, 猜0-100中的某个数,可以使用二分法。先猜50,大则猜25,小则猜75,然后再次二分。
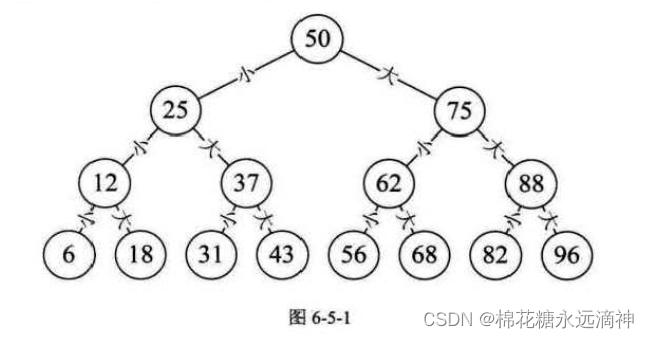
这种结构就叫二叉树结构。二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树的特点有:
①每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。注意不是只有两棵子树,而是最多有。没有子树或者有一棵子树都是可以的。
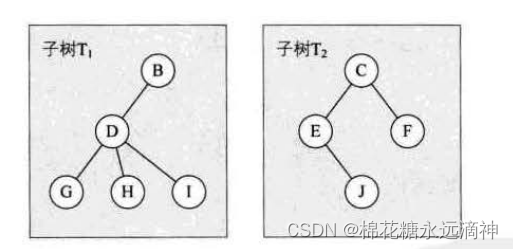
②左子树和右子树是有顺序的,次序不能任意颠倒。就像人是双手、双脚,但显然左手、左脚和右手、右脚是不一样的,右手戴左手套、右脚穿左鞋都会极其别扭和难受。
③即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。图6-5-3中,树1和树2是同一棵树,但它们却是不同的二叉树。就好像你一不小心,摔伤了手,伤的是左手还是右手,对你的生活影响度是完全不同的。
2.二叉树的特殊形态
(1)斜树
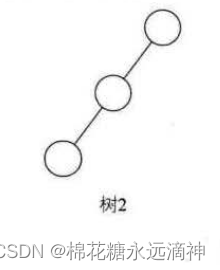
斜树是一种特殊的二叉树,所有的节点都只有左子节点或右子节点,没有同时拥有左子节点和右子节点的节点。斜树可以分为左斜树和右斜树,具体取决于所有节点只有左子节点或右子节点。
(2)满二叉树
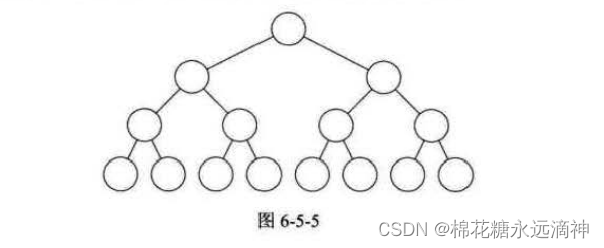
满二叉树是一种特殊的二叉树,除了叶节点外,每个节点都有两个子节点。满二叉树的特点是所有的叶节点都在同一层上,并且除了叶节点外,每个节点的度数都是2。
(3)完全二叉树
完全二叉树是一种特殊的二叉树,除了最后一层外,其他层的节点都是满的,且最后一层的节点都靠左排列。也可以说,完全二叉树是一颗二叉树中,从上到下、从左到右依次填满节点的二叉树。
3.二叉树的性质
二叉树具有以下性质:
每个节点最多有两个子节点:每个节点最多有两个子节点,分别称为左子节点和右子节点。如果一个节点没有子节点,称为叶节点。
左子树和右子树的顺序不能颠倒:二叉树的左子树和右子树的顺序不能颠倒,即左子节点在右子节点之前。
每个节点的子树也是二叉树:二叉树的每个节点的子节点也是二叉树,即每个节点都可以看作是根节点。
二叉树的高度:二叉树的高度是指从根节点到最深叶节点的路径上的节点数。树中的节点数目为n,那么二叉树的高度最大为n-1,最小为log2(n+1)。
二叉树的遍历:二叉树的遍历有三种常用的方式,分别是前序遍历、中序遍历和后序遍历。前序遍历先访问根节点,然后递归访问左子树和右子树。中序遍历先递归访问左子树,然后访问根节点,最后递归访问右子树。后序遍历先递归访问左子树和右子树,最后访问根节点。
二叉搜索树(Binary Search Tree,简称BST):二叉搜索树是一种特殊的二叉树,其中每个节点的值都大于其左子树中的任意节点的值,且小于其右子树中的任意节点的值。这使得在二叉搜索树中进行搜索、插入和删除操作的时间复杂度为O(logn),其中n为树中节点的数量。
4.二叉树的存储结构
链式结构,一个数据域,两个指针域,分别存放指向左孩子和右孩子的指针。

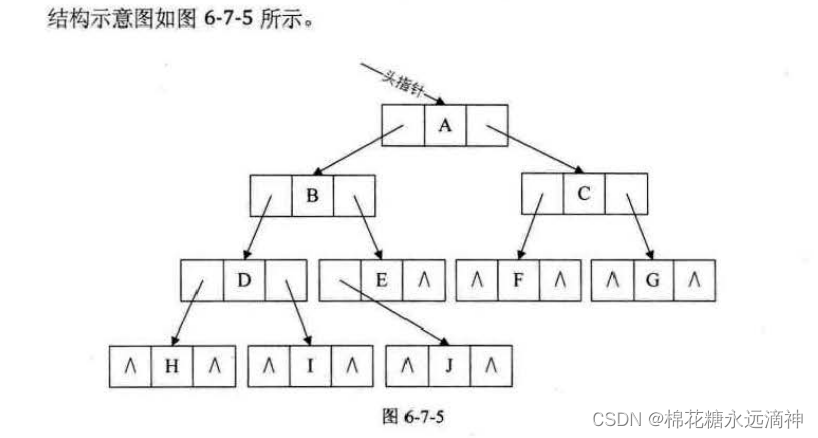
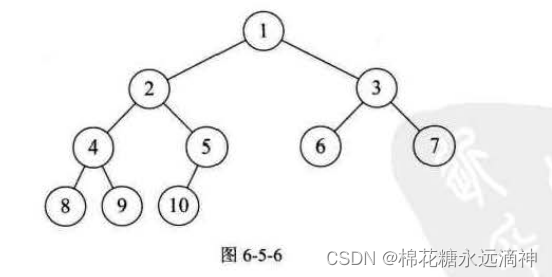
5.二叉树的遍历算法(前序、中序、后序)
①前序遍历
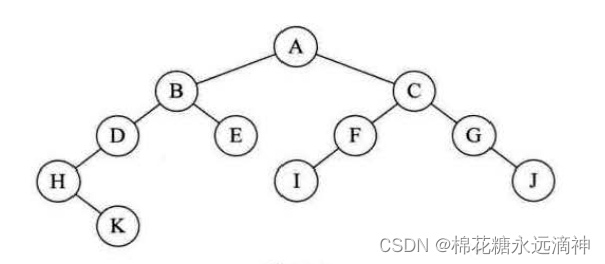
关键思路就是:先根结点,再左后右。(根节点不是指A,指的是每一次遍历到的当前结点就看作根节点)
遍历每个结点的顺序是:ABDHKECFIGJ
②中序遍历:
关键思路是:先左后根节点,再右节点。

遍历每个结点的顺序是:HKDBEAIFCGJ
③后序遍历:
关键思路是:先左再右,根节点最后访问。

遍历每个结点的顺序是:KHDEBIFJGCA
6.已知前序/中序/后序三者中的其二,求另外一个
不过多解释,反正用脑子分析就行。理解原理,然后就跟推理一样,慢慢分析即可。
注意:已知前序和后序,无法求出中序。
7.建立一颗二叉树
#include <stdio.h>
#include <stdlib.h>// 定义二叉树节点结构体
typedef struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;
} TreeNode;// 创建二叉树节点
TreeNode* createNode(int val) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));if (newNode == NULL) {printf("内存分配失败\n");exit(1);}newNode->val = val;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 构建二叉树
TreeNode* buildTree() {int val;printf("输入节点的值(输入-1表示空节点):");scanf("%d", &val);if (val == -1) {return NULL;}TreeNode* root = createNode(val);printf("构建左子树:\n");root->left = buildTree();printf("构建右子树:\n");root->right = buildTree();return root;
}
思路:buildTree 函数可以递归地创建左右子节点是因为在构建二叉树的过程中,每次调用 buildTree 函数都是在当前节点的基础上构建其左右子树。
具体来说,函数首先提示用户输入节点的值,如果输入值为 -1,则表示该节点为空,返回 NULL。否则,创建一个新的节点,并递归地调用 buildTree 函数来构建当前节点的左子树和右子树。
在递归调用中,每次调用都会创建一个新的节点,并将其赋值给当前节点的左子树或右子树指针。然后,在新的节点上,再次调用 buildTree 函数来构建其左子树和右子树。这样,通过递归的方式,就可以逐层构建整个二叉树的节点。
当用户输入 -1 表示节点为空时,会逐层返回 NULL,即构建空节点。这样,递归调用结束后,就完成了整个二叉树的构建过程。
六、线索二叉树
线索二叉树是对二叉树的一种改进,它通过添加线索(thread)来加快对二叉树的遍历操作。线索二叉树中,除了存储节点的值和左右子树指针外,还添加了线索指针,用于指向前驱节点或后继节点。
具体来说,线索二叉树中的线索指针可以分为两种类型:
前驱线索:对于每个节点,线索指针可以指向其在中序遍历中的前驱节点。
后继线索:对于每个节点,线索指针可以指向其在中序遍历中的后继节点。
线索化二叉树的过程主要包括两个步骤:
线索化左子树:在线索化当前节点的左子树时,需要将当前节点的前驱线索指针指向其在中序遍历中的前驱节点,并将前驱线索指针的后继线索指针指向当前节点。
线索化右子树:在线索化当前节点的右子树时,需要将当前节点的后继线索指针指向其在中序遍历中的后继节点,并将后继线索指针的前驱线索指针指向当前节点。
线索化完成后,可以通过线索指针直接找到任意节点的前驱节点和后继节点,从而加速对二叉树的遍历操作。
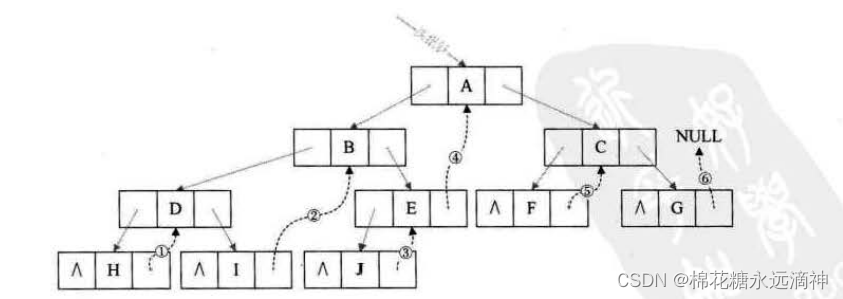
七、赫夫曼树
赫夫曼树(Huffman Tree),也称为最优二叉树(Optimal Binary Tree),是一种特殊的二叉树结构,常用于数据压缩算法中的赫夫曼编码。
赫夫曼树的构建过程基于赫夫曼算法,其核心思想是将出现频率较高的字符或数据项放在离根节点较近的位置,而出现频率较低的字符或数据项放在离根节点较远的位置,以实现高效的压缩。
具体构建赫夫曼树的步骤如下:
给定一组字符或数据项及其出现频率,根据频率从小到大排序,作为初始的叶子节点集合。
从初始的叶子节点集合中选择出现频率最小的两个节点作为左右子节点,并创建一个新的节点作为它们的父节点,父节点的频率为左右子节点频率之和。
将父节点加入到叶子节点集合中,并从集合中删除被合并的两个子节点。
重复步骤2和步骤3,直到只剩下一个节点,该节点即为赫夫曼树的根节点。
赫夫曼树的构建过程可以通过使用优先队列(Priority Queue)来实现,每次从队列中选择频率最小的两个节点进行合并。
赫夫曼树的特点是,出现频率较高的字符或数据项在树中的路径较短,而出现频率较低的字符或数据项在树中的路径较长。这样,在进行赫夫曼编码时,可以用较短的编码表示较高频率的字符或数据项,从而实现数据的压缩。
赫夫曼树在数据压缩中具有重要的应用,能够有效地压缩数据并保证数据的可恢复性。
具体的赫夫曼树的图解、代码实现、性质作用等内容以后有机会再补充,这里仅了解一下。
相关文章:

数据结构与算法C语言版学习笔记(6)-树、二叉树、赫夫曼树
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树的定义1.结点的度、树的度2.结点的逻辑关系3.树的深度4.有序树和无序树5.森林 二、树的存储结构(1)双亲表示法(2&…...
Leetcode刷题详解——电话号码的字母组合
1. 题目链接:17. 电话号码的字母组合 2. 题目描述: 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。…...

dream_ready
🧸欢迎来到dream_ready的博客,📜相信您对这篇博客也感兴趣o (ˉ▽ˉ;) Python 语法及入门 (超全超详细) 专为Python零基础 一篇博客让你完全掌握Python语法 路的尽头是什么?这是我年少时常伴在嘴…...
离线视频ocr识别
sudo apt-get install libleptonica-dev libtesseract-dev sudo apt-get install tesseract-ocr-chi-sim python -m pip install video-ocrwindows安装方法: 下载安装 https://digi.bib.uni-mannheim.de/tesseract/tesseract-ocr-w64-setup-5.3.3.20231005.exe 下…...

双十一流量卡选购指南:不要只看月租,性价比高才是硬道理!
双十一来了,流量卡也推出了不少性价比较高的套餐,为了方便大家选择,这篇文章给大家推荐如何流量卡,希望大家都能够买到合适自己的流量卡,不该花的钱坚决不花! 这篇文章内容较多,请大家耐…...

时序预测 | MATLAB实现WOA-CNN-GRU-Attention时间序列预测(SE注意力机制)
时序预测 | MATLAB实现WOA-CNN-GRU-Attention时间序列预测(SE注意力机制) 目录 时序预测 | MATLAB实现WOA-CNN-GRU-Attention时间序列预测(SE注意力机制)预测效果基本描述模型描述程序设计参考资料 预测效果 基本描述 1.MATLAB实现…...
华为防火墙二层透明模式下双机热备负载分担配置(两端为路由器)
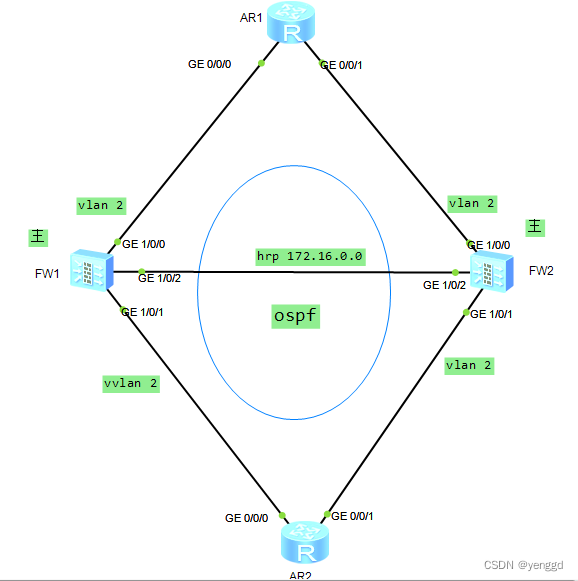
这种模式只做负载分担,不能是主备备份,因为主备备份模式下,备设备会把vlan down掉,如果是主备备份模式,那在主挂后,备的状态在切换过程中先起vlan,再建立ospf邻接,那业务会断线较久&…...

“基于RflySim平台飞控底层算法开发”系列专题培训 (第三期)
>> RflySim平台系列专题培训 RflySim平台是一个生态系统或工具链(官网:https://doc.rflysim.com),发起于北航可靠飞行控制研究组,主要用于遵循基于模型设计的思想进行无人系统的控制和安全测试。本平台选择MATL…...
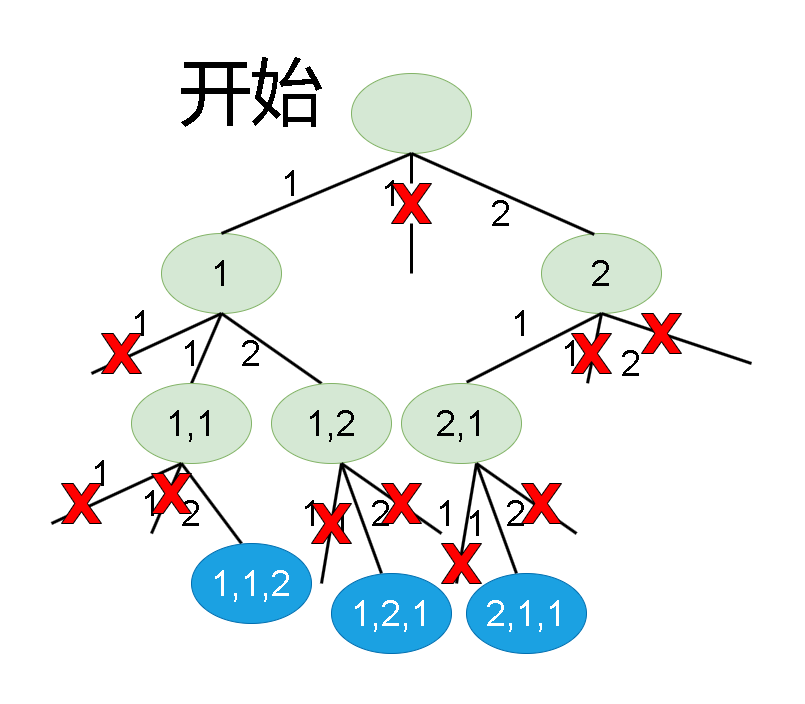
Leetcode刷题详解——全排列 II
1. 题目链接:47. 全排列 II 2. 题目描述: 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]示例 2: 输…...
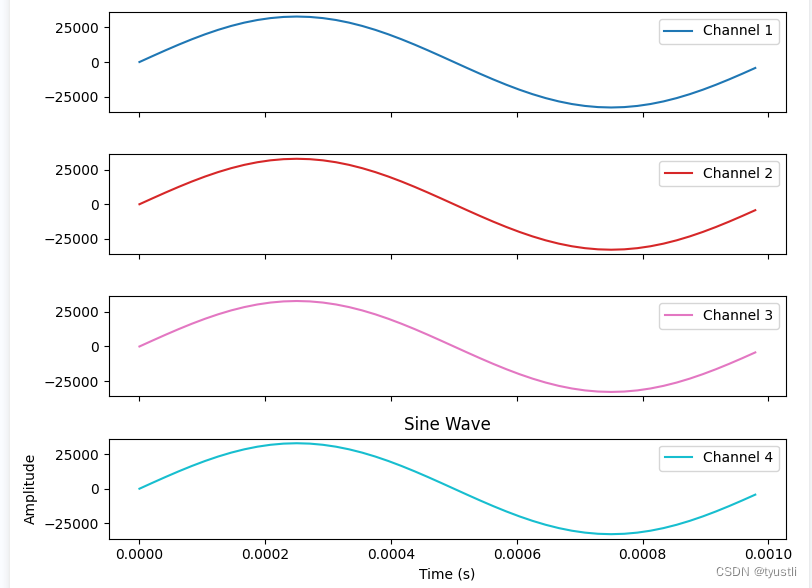
音频——解析 PCM 数据
文章目录 生成 PCM 数据16bit16bit mono16bit stereo16bit 4 channel16bit 8 channel24bit解析 PCM 数据解析 24bit 数据程序源码生成 PCM 源码解析 PCM 源码生成 PCM 数据 16bit 16bit mono int 48k_16bit_modo[] = {0, 4276, 8480, 12539, 16383, 19947, 23169, 25995, 28…...
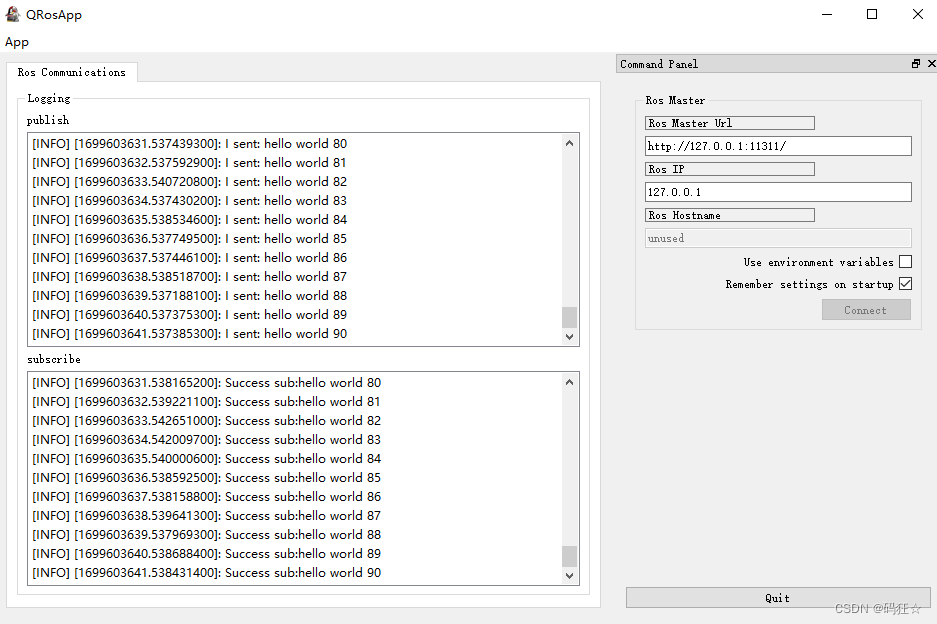
win10 下 ros + Qt 工程CMakeLists.txt
win10 下 ros Qt 工程CMakeLists.txt 系统:win10 ros: melodic Qt: 5.12.12 源码目录: D:\workspace\catkin_qt 示例代码 https://github.com/ncnynl/ros-qt.git 由于示例代码是Qt4 ,目前我是用QT5,所以CMakeLists.txt 修改如下 CMakeLists.txt #####…...

Scala中编写多线程爬虫程序并做可视化处理
目录 一、引言 二、Scala爬虫程序的实现 1、引入必要的库 2、定义爬虫类 3、可视化处理 三、案例分析:使用Scala爬取并可视化处理电影数据 1、定义爬虫类 2、实现爬虫程序的控制逻辑 3、可视化处理电影数据 四、总结 一、引言 随着互联网的快速发展&#…...

使用 huggingface_hub 镜像下载 大模型
download.py 👇 import os # 配置 hf镜像 os.environ[HF_ENDPOINT] https://hf-mirror.com# 设置保存的路径 local_dir "XXXXXX"# 设置仓库id model_id "sensenova/piccolo-large-zh"cmd f"huggingface-cli download --resume-downlo…...
,剑指offer,力扣)
路径加密(替换空格),剑指offer,力扣
目录 我们直接看题解吧: 方法: 审题目事例提示: 解题思路: 法1: 代码(法1): 法2: 代码(法2): 原题解: 【剑指Offer】2、替…...
HarmonyOS开发:UI开展前的阶段总结
前言 关于HarmonyOS,陆陆续续总结了有14篇的文章,大家可以发现,没有一篇是关于UI相关的,不是自己没有分享的打算,而是对于这些UI而言,官方都有着一系列的文档输出,如果我再一一的分享࿰…...

Linux安装Libreoffice
windos安装Libreoffice https://zh-cn.libreoffice.org/ C:\路径\LibreOffice\program\soffice.bin --help 看是否输出帮助命令 Linux安装Libreoffice 1、下载rpm包并解压https://mirrors.cloud.tencent.com/libreoffice/libreoffice/stable/ 2、安装: yum install…...
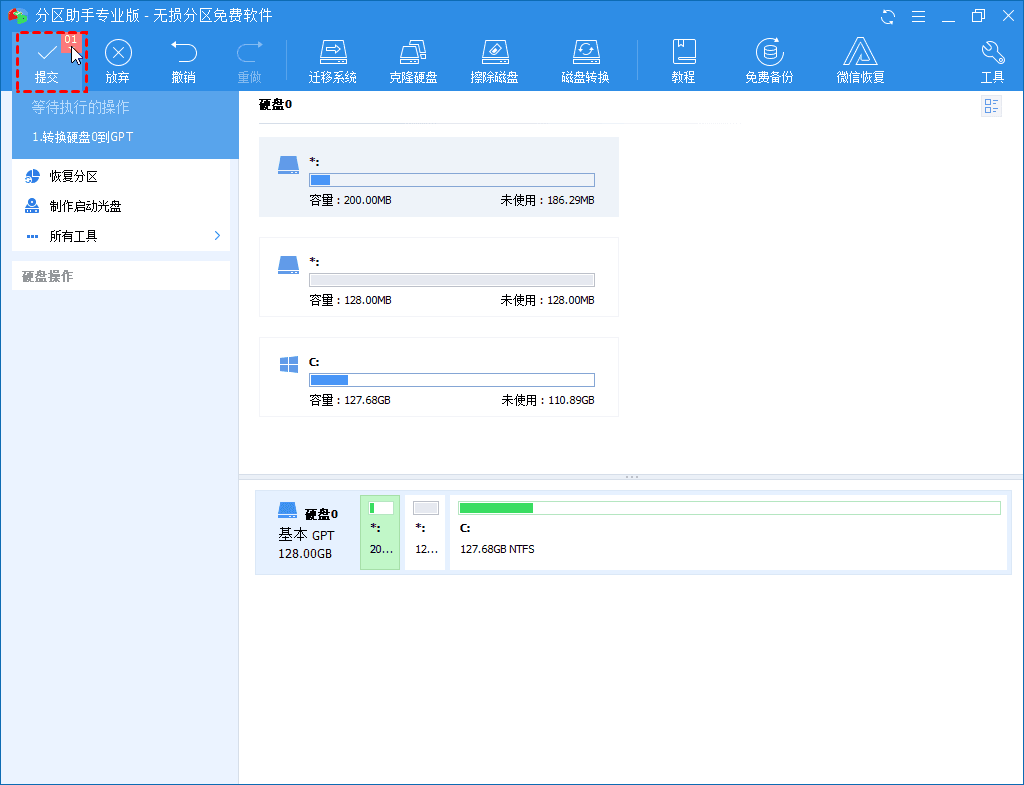
如何将系统盘MBR转GPT?无损教程分享!
什么是MBR和GPT? MBR和GPT是磁盘的两种分区形式:MBR(主引导记录)和GPT(GUID分区表)。 新硬盘不能直接用来保存数据。使用前应将其初始化为MBR或GPT分区形式。但是,如果您在MBR时需…...
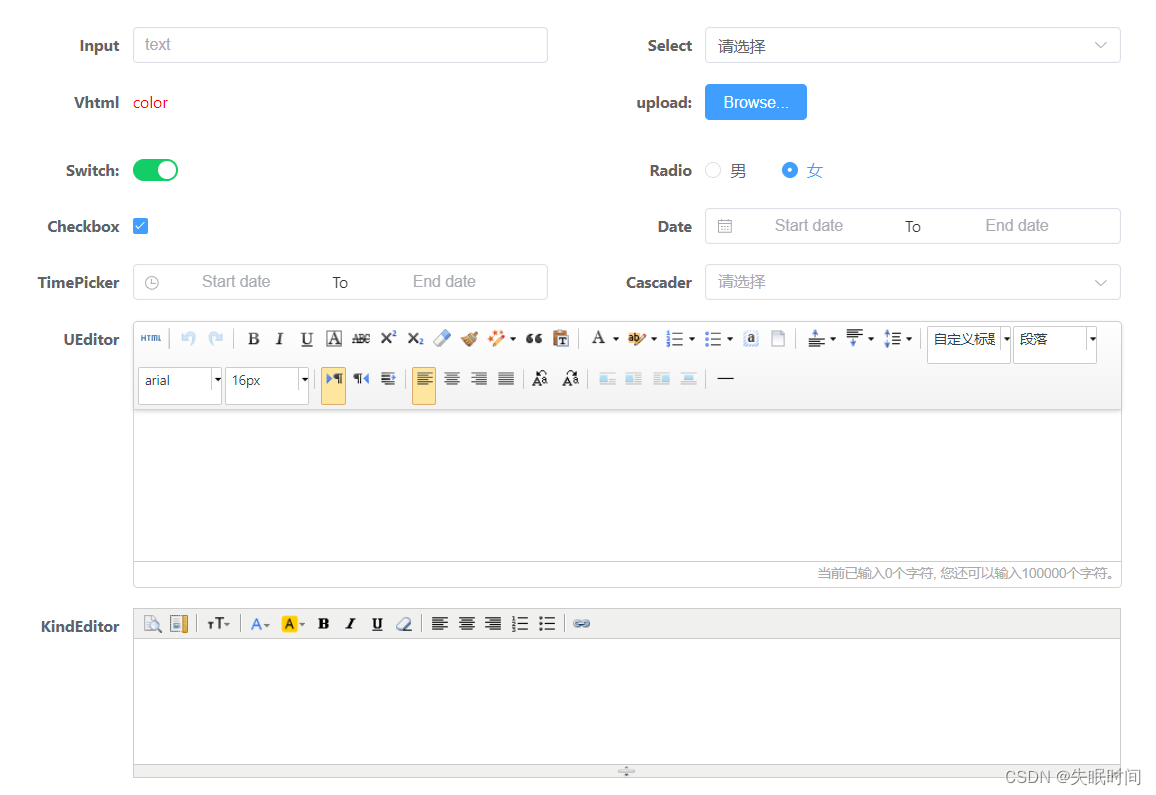
基于element-plus定义表单配置化
文章目录 前言一、配置化的前提二、配置的相关组件1、新建form.vue组件2、新建input.vue组件3、新建select.vue组件4、新建v-html.vue组件5、新建upload.vue组件6、新建switch.vue组件7、新建radio.vue组件8、新建checkbox.vue组件9、新建date.vue组件10、新建time-picker.vue组…...
|LeetCode122. 买卖股票的最佳时机 II、LeetCoed55. 跳跃游戏、LeetCode45. 跳跃游戏 II)
LeetCode算法题解(贪心)|LeetCode122. 买卖股票的最佳时机 II、LeetCoed55. 跳跃游戏、LeetCode45. 跳跃游戏 II
一、LeetCode122. 买卖股票的最佳时机 II 题目链接:122. 买卖股票的最佳时机 II 题目描述: 给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。 在每一天,你可以决定是否购买和/或出售股票。你在任何时候 …...

计蒜客详解合集(2)期
目录 T1126——单词倒排 T1617——地瓜烧 T1612——蒜头君的数字游戏 T1488——旋转单词 T1461——校验信用卡号码 T1437——最大值和次大值 T1126——单词倒排 超级水的一道题,和T1122类似但更简单,分割后逆序输出即可~ 编写程序,读入…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
