springboot 虚拟线程demo
jd19支持虚拟线程,虚拟线程是轻量级的线程,它们不与操作系统线程绑定,而是由 JVM 来管理。它们适用于“每个请求一个线程”的编程风格,同时没有操作系统线程的限制。我们能够创建数以百万计的虚拟线程而不会影响吞吐。
做个 springboot demo 尝试一下。
环境
- jdk19
- gradle 7.6.1
- IntelliJ IDEA 2022.2.4
build.gradle
plugins {id 'java'id 'org.springframework.boot' version '3.0.3'id 'io.spring.dependency-management' version '1.1.0'
}group = 'com.example'
version = '0.0.1-SNAPSHOT'
sourceCompatibility = '19'configurations {compileOnly {extendsFrom annotationProcessor}
}repositories {mavenCentral()
}dependencies {implementation 'org.springframework.boot:spring-boot-starter'compileOnly 'org.projectlombok:lombok'developmentOnly 'org.springframework.boot:spring-boot-devtools'annotationProcessor 'org.projectlombok:lombok'testImplementation 'org.springframework.boot:spring-boot-starter-test'
}tasks.named('test') {useJUnitPlatform()
}tasks.withType(JavaCompile) {options.compilerArgs += "--enable-preview"
}多线程demo
写一段多线程调用的代码,程序入口
package com.example.myvirtualthreaddemo;import org.springframework.boot.CommandLineRunner;
import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;
import org.springframework.boot.autoconfigure.task.TaskExecutionAutoConfiguration;
import org.springframework.context.annotation.Bean;
import org.springframework.core.task.AsyncTaskExecutor;
import org.springframework.core.task.support.TaskExecutorAdapter;
import org.springframework.scheduling.annotation.EnableAsync;import java.util.concurrent.Executors;@EnableAsync
@SpringBootApplication
public class MyVirtualThreadDemoApplication {public static void main(String[] args) {SpringApplication.run(MyVirtualThreadDemoApplication.class, args);}@BeanCommandLineRunner commandLineRunner(AsyncService asyncService){return args -> {for(int i = 0; i < 100; i++){asyncService.fun(i);}};}
}package com.example.myvirtualthreaddemo;import lombok.extern.slf4j.Slf4j;
import org.springframework.scheduling.annotation.Async;
import org.springframework.stereotype.Service;@Service
@Slf4j
public class AsyncService {@Asyncpublic void fun(int i) {log.info("fun:{}", i);}
}
运行结果,使用平台线程(默认8个)
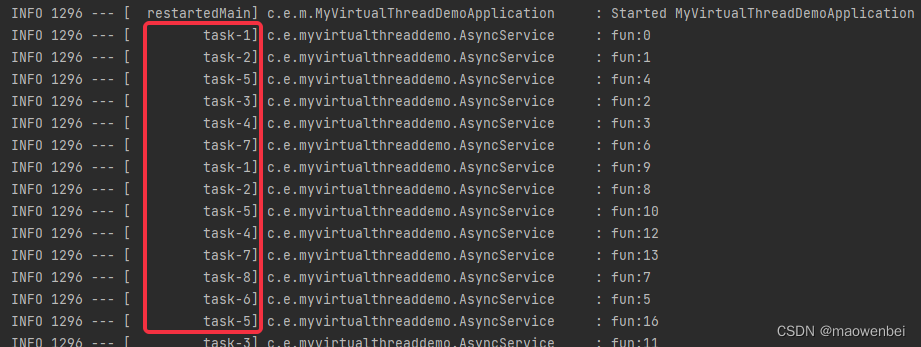
使用虚拟线程
在MyVirtualThreadDemoApplication添加以下代码块
@Bean(TaskExecutionAutoConfiguration.APPLICATION_TASK_EXECUTOR_BEAN_NAME)public AsyncTaskExecutor asyncTaskExecutor(){return new TaskExecutorAdapter(Executors.newVirtualThreadPerTaskExecutor());}
运行结果,使用虚拟线程
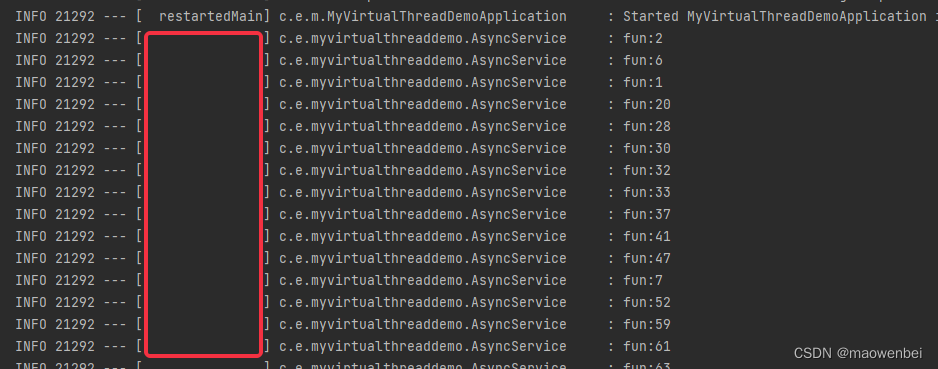
遇到的一些问题
请使用 --enable-preview 以启用预览 API
解决办法:
- build.gradle里添加以下配置:
tasks.withType(JavaCompile) {options.compilerArgs += "--enable-preview"
}
- 设置vm选项如图
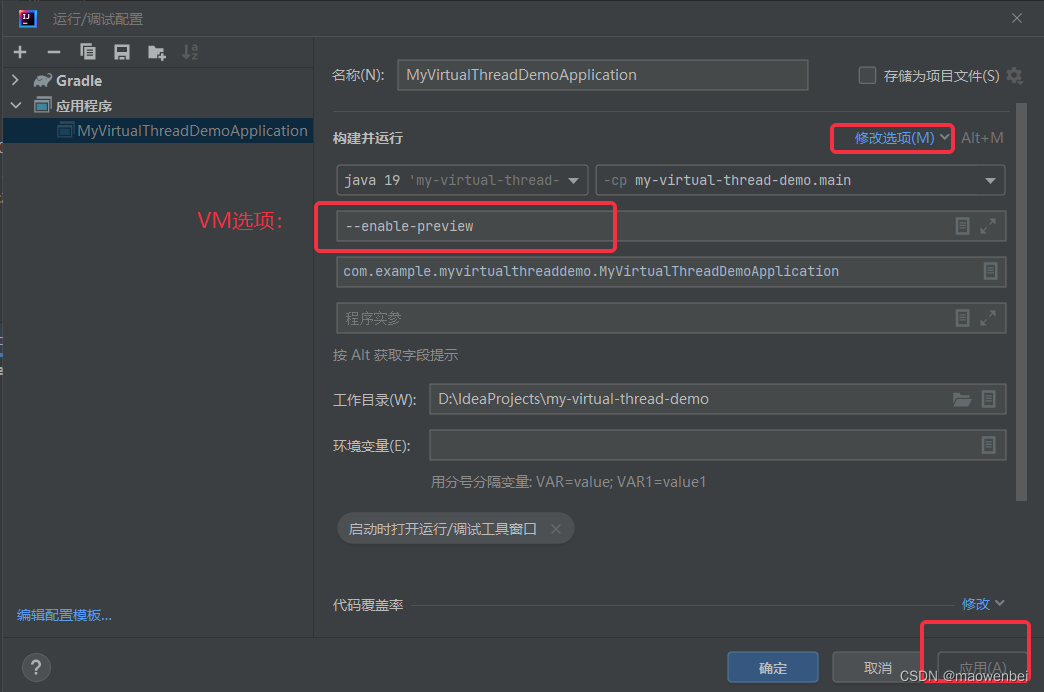
相关文章:

springboot 虚拟线程demo
jd19支持虚拟线程,虚拟线程是轻量级的线程,它们不与操作系统线程绑定,而是由 JVM 来管理。它们适用于“每个请求一个线程”的编程风格,同时没有操作系统线程的限制。我们能够创建数以百万计的虚拟线程而不会影响吞吐。 做个 spri…...

CTFer成长之路之逻辑漏洞
逻辑漏洞CTF 访问url: http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/ 登录页面用随意用户名密码登录 访问url: http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/user.php 登陆后有商品列表,共三个商品,点击购买flag 钱…...
)
入门力扣自学笔记238 C++ (题目编号:1144)
1144. 递减元素使数组呈锯齿状 题目: 给你一个整数数组 nums,每次 操作 会从中选择一个元素并 将该元素的值减少 1。 如果符合下列情况之一,则数组 A 就是 锯齿数组: 每个偶数索引对应的元素都大于相邻的元素,即 A…...

蓝桥杯-寒假作业
没有白走的路,每一步都算数🎈🎈🎈 题目描述: 有四个等式,每个等式的运算规则已经定好了,也就是我们常见的小学的四则运算,但是能够用来四则运算的数字非常有限,包括1~13…...
测试用例篇
1.测试用例的意义 测试用例(Test Case)是为了实施测试而向被测试的系统提供的一组集合,这组集合包含:测试环境、操作步骤、测试数据、预期结果等要素。 测试用例的意义是为了帮助测试人员了解测什么,怎么测 eg&#x…...

自动驾驶自主避障概况
文章目录前言1. 自主避障在自动驾驶系统架构中的位置2. 自主避障算法分类2.1 人工势场法(APF)2.1.1引力势场的构建2.1.2斥力势场的构建2.1.3人工势场法的改进2.2 TEB(Timed-Eastic-Band, 定时弹性带)2.3 栅格法2.4 向量场直方图(V…...

Python实用的库排名…
Python 是一个功能强大的编程语言,有着丰富的第三方库和模块,可以帮助你解决各种各样的问题。以下是一些比较厉害的 Python 库: NumPy:一个强大的数值计算库,提供了高效的数组和矩阵操作功能。 Pandas:提供…...
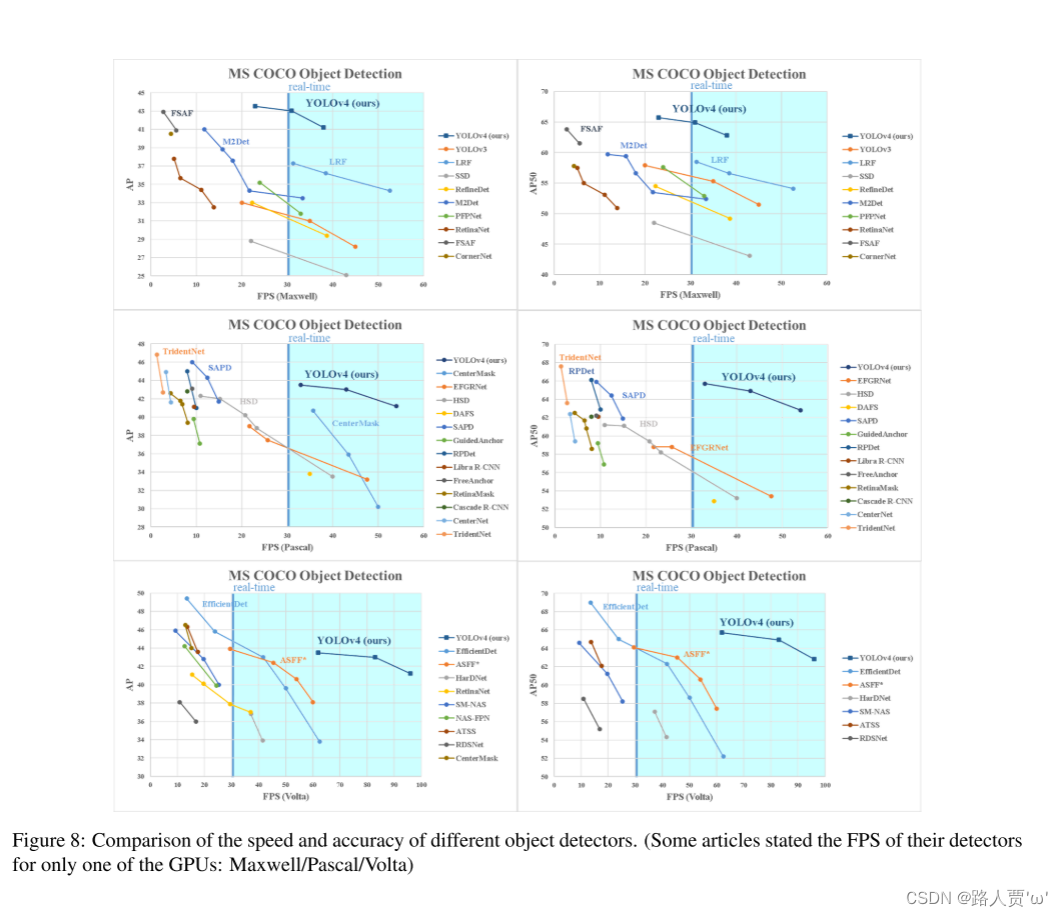
【YOLO系列】YOLOv4论文超详细解读1(翻译 +学习笔记)
前言 经过上一期的开篇介绍,我们知道YOLO之父Redmon在twitter正式宣布退出cv界,大家都以为YOLO系列就此终结的时候,天空一声巨响,YOLOv4闪亮登场!v4作者是AlexeyAB大神,虽然换人了,但论文中给出…...
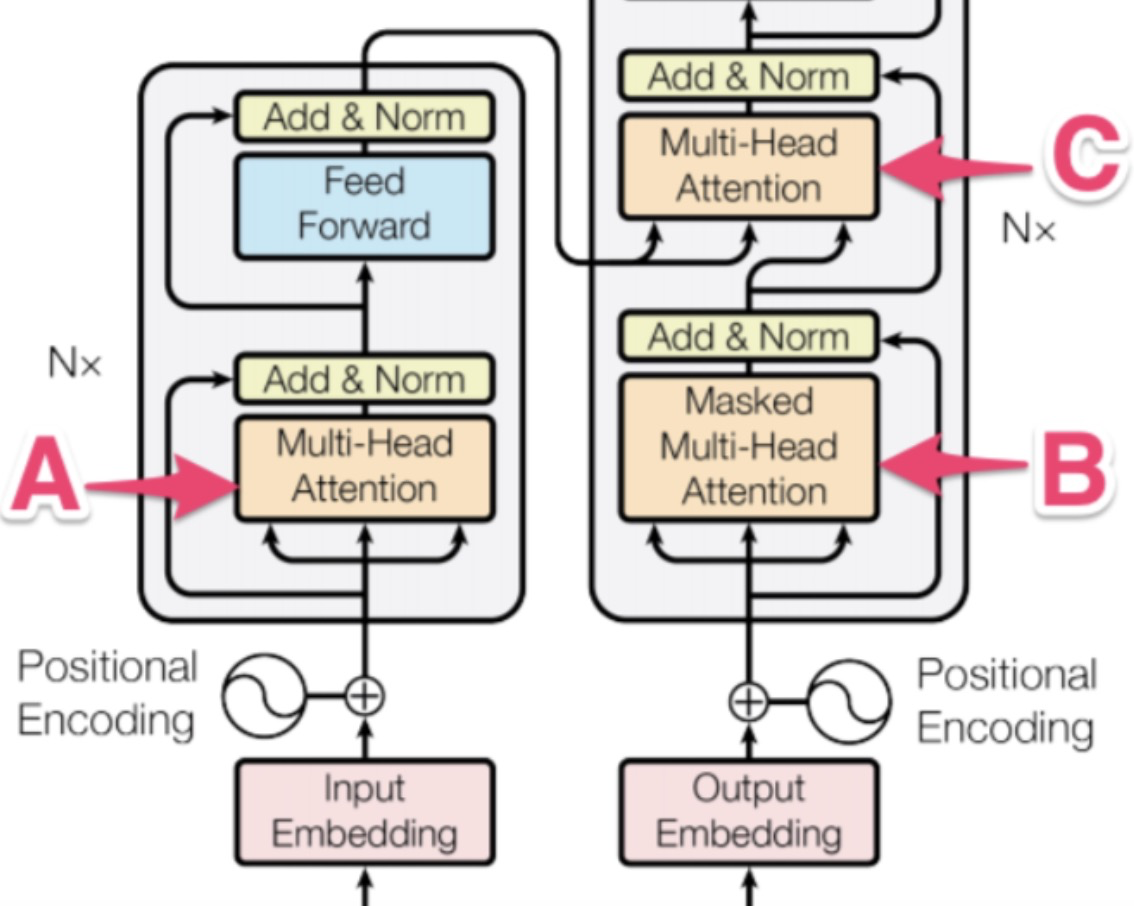
【神经网络】Transformer基础问答
1.Transforme与LSTM的区别 transformer和LSTM最大的区别就是LSTM的训练是迭代的,无法并行训练,LSTM单元计算完T时刻信息后,才会处理T1时刻的信息,T 1时刻的计算依赖 T-时刻的隐层计算结果。而transformer的训练是并行了࿰…...

制定防火墙策略的步骤和建议
制定防火墙策略是保护企业网络环境安全的关键一步。下面是一些制定防火墙策略的步骤和建议,供参考: 识别网络资产:确定企业网络环境中所有的网络资产,包括服务器、应用程序、数据库、移动设备和终端用户设备等,并进行…...
新必应(New Bing)国内申请与使用教程
微软的新必应(New Bing)基于GPT4模型,比ChatGPT的GPT3.5模型领先半个世代。并且集成了Edge浏览器的数据资源,功能更加强大。经过不断的踩坑,终于申请到了New Bing的使用权限,且国内网络也能够正常使用&…...
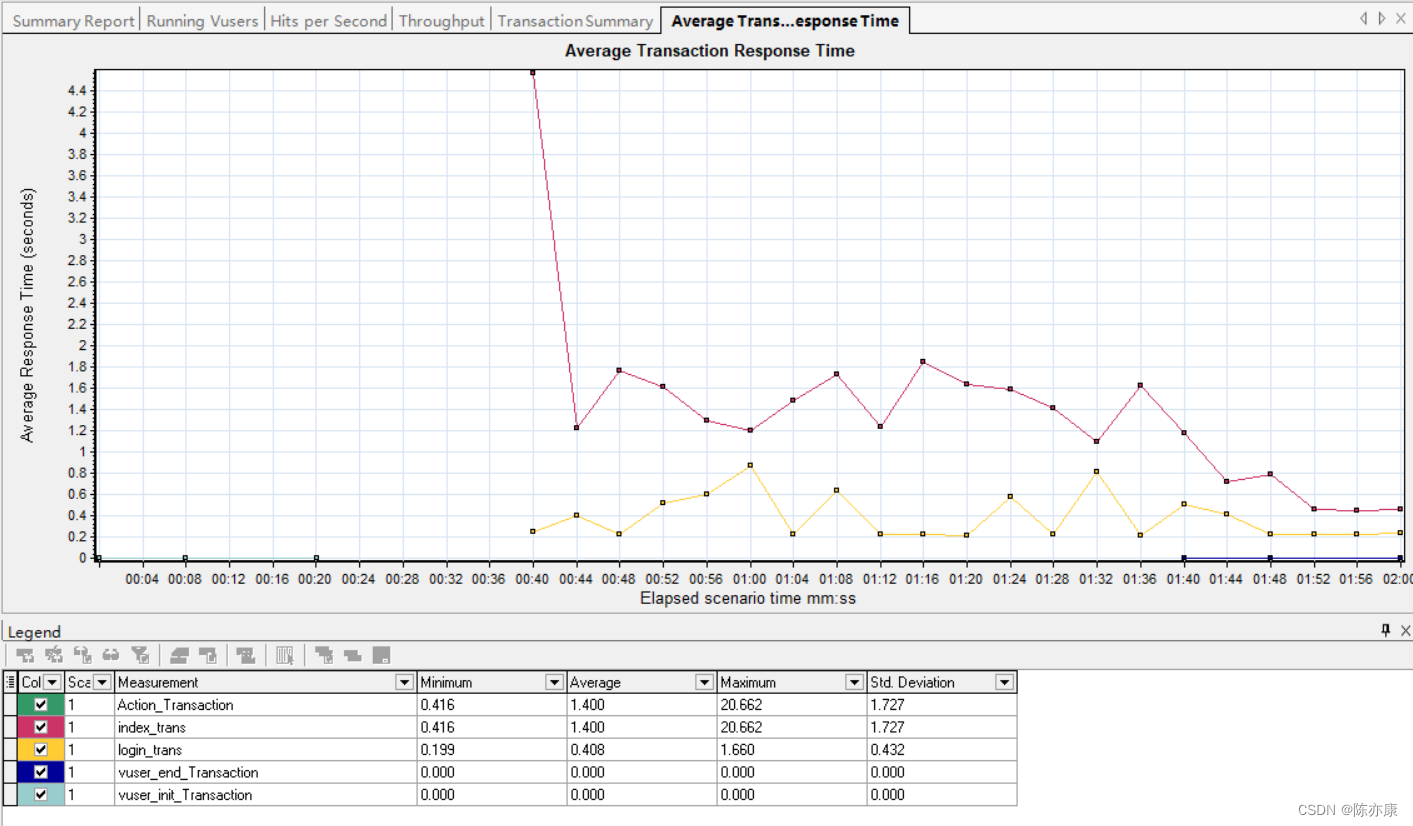
博客系统——项目测试报告
目录 前言 博客系统——项目介绍 1、测试计划 1.1、功能测试 1.1.1、编写测试用例 1.1.2、实际执行步骤 1.2、使用Selenium进行Web自动化测试 1.2.1、引入依赖 1.2.2、提取共性,实现代码复用 1.2.3、创建测试套件类 1.2.4、博客登录页自动化测试 1.2.5、…...
Macbook M1 安装PDI(Kettle) 9.3
Macbook M1 安装PDI(Kettle) 9.3 当前 PDI(Kettle)最新版为9.3,依赖Java JDK 11。因为没有专门用于 M1的程序,需要下载并安装x86_64架构的JDK及依赖软件,并 “强制在Intel模式下运行shell” 的方式来实现 Kettle 的正…...
机器学习——模型评估
在学习得到的模型投放使用之前,通常需要对其进行性能评估。为此,需使用一个“测试集”(testing set)来测试模型对新样本的泛化能力,然后以测试集上的“测试误差( tootino error)作为泛化误差的近似。我们假设测试集是从样本真实分…...
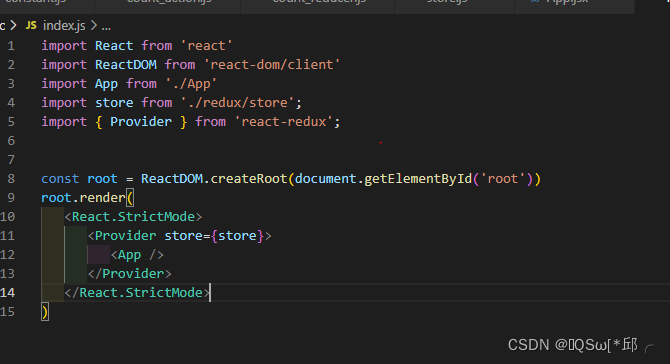
react react-redux学习记录
react react-redux学习记录1.原理2.怎么用呢2.1 容器组件2.2UI组件2.3 App.jsx3.简化3.1简写mapDispatch3.2 Provider组件的使用3.3整合UI组件和容器组件1.原理 UI组件:不能使用任何redux的api,只负责页面的呈现、交互等。 容器组件:负责和redux通信&…...
nodejs环境配置
啥是node.js 简单理解就是js运行环境 啥是npm 简单理解就是nodejs包管理工具,全称Node Package Manager 啥是cnpm npm的开源镜像,在国内使用cnpm替代npm可以起到加速的效果 https://npmmirror.com/ ①安装node.js https://nodejs.org/en/download/ 下载…...

数据治理之元数据管理Atlas
数据治理之元数据管理的利器——Atlas 一、数据治理与元数据管理 1.1 背景 为什么要做数据治理? 业务繁多,数据繁多,业务数据不断迭代。人员流动,文档不全,逻辑不清楚,对于数据很难直观理解,…...

15 Nacos客户端实例注册源码分析
Nacos客户端实例注册源码分析 实例客户端注册入口 流程图: 实际上我们在真实的生产环境中,我们要让某一个服务注册到Nacos中,我们首先要引入一个依赖: <dependency><groupId>com.alibaba.cloud</groupId>&l…...

C++将派生类赋值给基类(向上转型)
1.将派生类对象赋值给基类对象 #include <iostream> using namespace std;//基类 class A{ public:A(int a); public:void display(); public:int m_a; }; A::A(int a): m_a(a){ } void A::display(){cout<<"Class A: m_a"<<m_a<<endl; }//…...

使用Platform Designer创建Nios II 最小系统
Nios II简介 Nios II 软核处理器十多年前就有了,它和xilinx的MicroBlaze类似,性能相比硬核处理器要差得多,工程应用也不是很多,那还有必须学习一下吗?我个人认为了解一下Nios II开发流程,对intel FPGA开…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
