AlGaN/GaN HFET 五参数模型
标题:A Five-Parameter Model of the AlGaN/GaN HFET
来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(15年)
摘要—我们引入了AlGaN/GaN异质结场效应晶体管(HFET)漏极电流Id(Vgs,Vds)的解析表达式,该表达式是其栅极和漏极电压的函数。我们从HFET的紧凑物理模型中推导出这个函数。所提出的电流表达式由五个参数配置,这些参数可以用器件的几何形状和材料来表示。我们通过将其嵌入表示端子馈送阻抗和器件寄生参数的12参数RLC网络,将模型扩展到小信号射频操作。我们调整扩展模型的参数,以同时拟合工业晶体管的直流和射频测量数据。
索引术语—AlGaN/GaN,解析,紧凑模型,连续可微,直流,HEMT,异质结场效应晶体管(HFET),物理,基于物理的,射频。
文章研究了什么
该文章研究了AlGaN/GaN HFET(高电子迁移率晶体管)的理想模型及其在不同条件下的行为。
- 该模型排除了击穿、电荷储存、自热、亚阈值、短沟道和捕获效应。
- 通过使用一个包含12个参数的RLC嵌入电路,将该模型扩展到射频,并拟合到一个器件的测量数据,包括直流I-V、S11、S22和S21。
- 该模型与测量结果显示出极好的一致性,仅在高频和低频时存在轻微差异,分别归因于系统误差和电子捕获。
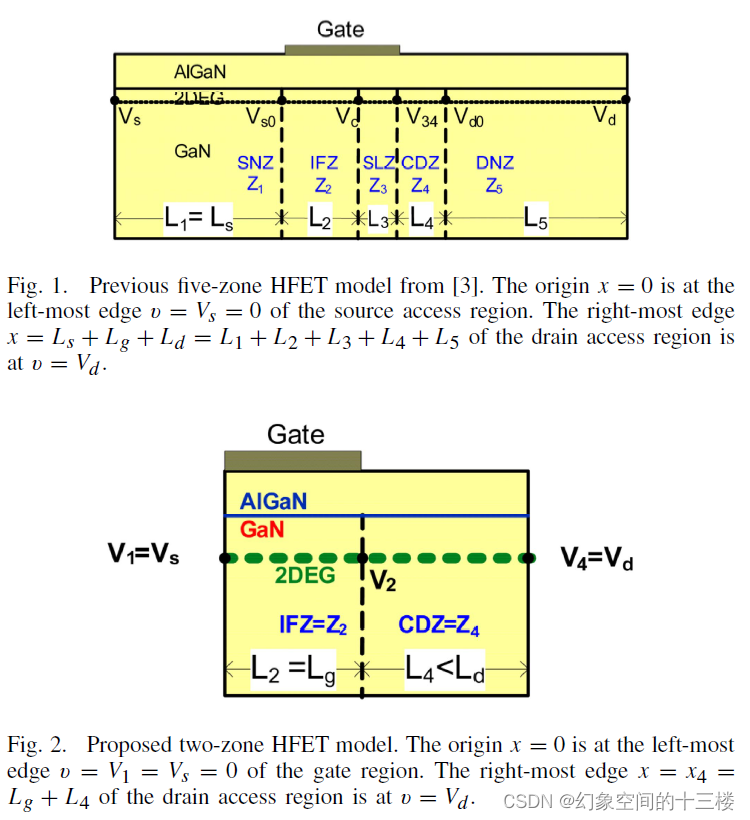
- 所提出的模型由两个区域组成:源中性区(Z1)和本征FET区(Z2),遵循肖克利方程。
- 该模型还包括一个空间电荷受限区(Z3),在这里载流子输运受到空间电荷限制,电子速度有效饱和。
- 通过模拟和测量的S21幅度和相位,以及直流扫描和阶跃响应的验证,证明了该模型的有效性。
文章的创新点
- 该文章提出了一个理想的AlGaNGaN HFET模型,排除了击穿、电荷储存、自热、亚阈值、短沟道和捕获效应等各种影响。这种方法简化了对器件行为的表示,使其更为准确。
- 通过使用包含12个参数的RLC嵌入电路,将该模型扩展到射频,从而实现对器件在高频下性能的表征。这一扩展为HFET的射频行为提供了有价值的见解。
- 所提出的模型通过拟合一个器件的测量数据,包括直流I-V、S11、S22和S21,与实验数据取得了极好的一致性。这证明了模型在捕捉器件特性方面的有效性和准确性。
- 该文章还引入了一个AlGaNGaN HFET的五参数模型,提供了对器件行为的简化表示。这个模型可用于对HFET性能进行快速高效的分析。
- 文章提出了一个先前的五区HFET模型,作为对所提出的理想模型的参考。这种比较突显了当前研究中取得的改进和进展。
文章的研究方法
- 该文章采用了分析方法,以开发AlGaNGaN HFET的理想模型。该模型排除了各种影响,如击穿、电荷储存、自热、亚阈值、短沟道和捕获效应。
- 通过使用包含12个参数的RLC嵌入电路,将该模型扩展到射频,从而允许对器件在高频下的行为进行表征。
- 所提出的模型通过拟合一个器件的测量数据,包括直流I-V、S11、S22和S21,以验证其准确性和有效性。
- 文章还提出了一个先前的五区HFET模型,作为所提出的理想模型的参考,突显了当前研究中取得的进展。
总体而言,研究方法涉及开发一个理想模型,将其扩展到射频,并通过对一个器件的测量进行验证。
文章的结论
- 该文章首次通过提出并解决HFET中导电物理的核心概念模型,解释了AlGaNGaN HFET中的大信号晶体管效应。该模型由两个区域Z4和Z2组成,它们由表示栅的漏端边缘的点x=Lg分隔。参数Lg、a、im、b和Vto可以用HFET的物理几何形状和材料表示,并被调整为等效电路参数,以同时拟合单个器件的直流和射频测量数据。
- 文章通过排除各种效应,如击穿、电荷储存、自热、亚阈值、短沟道和捕获效应,为这个理想模型报告了一个精确的解。该模型在分析上近似,并通过使用包含12个参数的RLC嵌入电路扩展到射频,该电路被拟合到一个器件的直流I-V、S11、S22和S21测量中,与实验数据显示出极好的一致性。
- 所提出的模型及其对实验数据的拟合展示了这种方法在捕捉AlGaNGaN HFET行为方面的有效性和准确性,为理解其性能提供了有价值的见解。
相关文章:

AlGaN/GaN HFET 五参数模型
标题:A Five-Parameter Model of the AlGaN/GaN HFET 来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(15年) 摘要—我们引入了AlGaN/GaN异质结场效应晶体管(HFET)漏极电流Id(Vgs,Vds…...
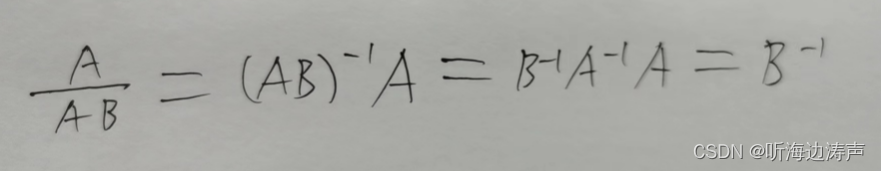
矩阵的除法
B/A 如果矩阵A可逆,那么 证明: A/AB 如果矩阵A和B都可逆,那么 证明:...

Java中的 向上转型 | 向下转型
目录 一.向上转型 直接赋值 总结: 通过传参 通过返回值 二.向下转型 instanceof 一.向上转型 向上转型其实就是创建一个子类对象,并将其当作父类对象来使用,一般语法格式如下: 父类类型 对象名 new 子类类型() 一般有以…...
)
【华为OD机试AB高分必刷题目】朋友圈(C++-并查集Union-Find实现)
🚀你的旅程将在这里启航!本专栏所有题目均包含优质解题思路,高质量解题代码,详细代码讲解,助你深入学习,高分通过! 文章目录 【华为OD机试AB高分必刷题目】朋友圈(C++-并查集Union-Find实现)题目描述解题思路C++题解代码代码OJ评判结果代码讲解寄语【华为OD机试AB高分…...

前端面试题之vue篇
vue基础 vue的基本原理 当一个Vue实例创建时,Vue会遍历data中的属性,用Object.defineProperty(Vue使用proxy)转换为getter/setter,并且在内部追踪相关依赖,在属性被访问和修改时通知变化。每个组件实例都有相应的watcher程序实例…...
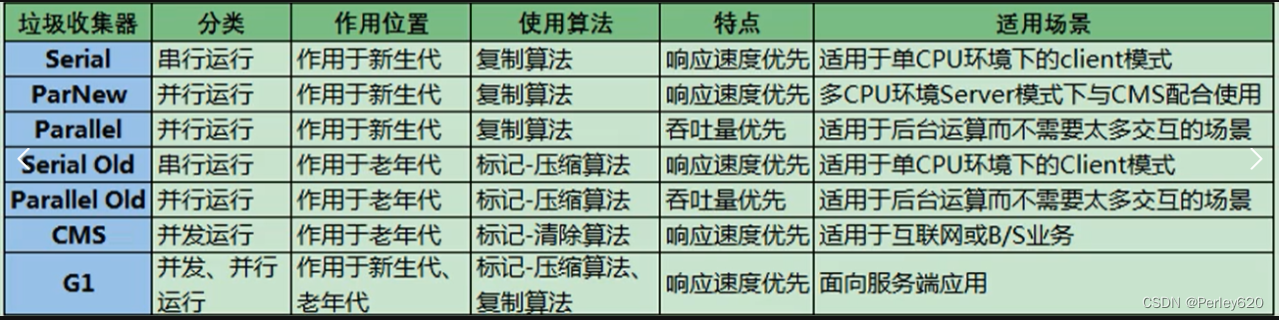
Java进阶(垃圾回收GC)——理论篇:JVM内存模型 垃圾回收定位清除算法 JVM中的垃圾回收器
前言 JVM作为Java进阶的知识,是需要Java程序员不断深度和理解的。 本篇博客介绍JVM的内存模型,对比了1.7和1.8的内存模型的变化;介绍了垃圾回收的语言发展;阐述了定位垃圾的方法,引用计数法和可达性分析发以及垃圾清…...
GaN HEMT 电容的分析建模,包括寄生元件
标题:Analytical Modeling of Capacitances for GaN HEMTs, Including Parasitic Components 来源:IEEE TRANSACTIONS ON ELECTRON DEVICES(14年) 摘要:本文提出了一种基于表面势的终端电荷和电容模型,包…...

Python实战 | 使用 Python 和 TensorFlow 构建卷积神经网络(CNN)进行人脸识别
专栏集锦,大佬们可以收藏以备不时之需 Spring Cloud实战专栏:https://blog.csdn.net/superdangbo/category_9270827.html Python 实战专栏:https://blog.csdn.net/superdangbo/category_9271194.html Logback 详解专栏:https:/…...
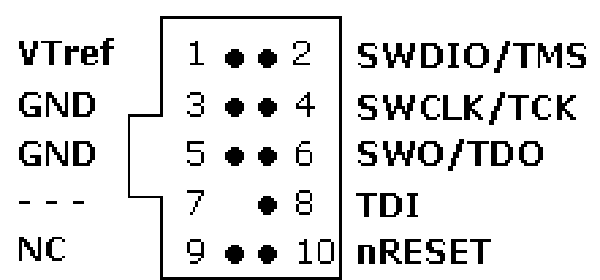
JLink edu mini 10Pin接口定义
注意:SWD接口在阵脚2,4;而20Pin的SWD接口在阵脚7,9 参考:1 官网资料; 2 【润石RS0104YQ Demo开发板测试分享】J-Link EDU Mini调试5V系统_国产运算放大器_模拟开关_线性稳压器_电平转换器_小逻辑_比较器…...

compile: version “go1.19“ does not match go tool version “go1.18.1“
** 1 安装了新版本的go后 为什么go version 还是旧版本? ** 如果你已经按照上述步骤安装了新版本的 Go,但 go version 命令仍然显示旧版本,可能是因为你的环境变量设置不正确或未正确生效。你可以尝试以下方法来解决问题: 重新…...

spring boot security 自定义AuthenticationProvider
spring boot security 自定义AuthenticationProvider 基于 spring boot 3.x 场景实现 手机验证码登陆 实现 CaptureCodeAuthenticationFilter public class CaptureCodeAuthenticationFilter extends AbstractAuthenticationProcessingFilter {private static final Strin…...

某电力设计公司绩效考核优化项目成功案例纪实
——引入角色定位考核法,建立多维度评价体系,支持业务转型后的客观评价 【客户行业】电力行业 【问题类型】绩效考核 【客户背景及现状分析】 某电力设计公司成立于2000年左右,是一家从事输变电工程勘察、设计、咨询的专业公司,…...

力扣371周赛
力扣第371场周赛 找出强数对的最大异或值 I 枚举 class Solution { public:int maximumStrongPairXor(vector<int>& a) {int n a.size() , res 0;for(int i 0 ; i < n ; i ){for(int j 0 ; j < n ; j ){if(abs(a[i]-a[j])<min(a[i],a[j])){int c (a…...

Python之字符串、正则表达式练习
目录 1、输出随机字符串2、货币的转换(字符串 crr107)3、凯撒加密(book 实验 19)4、字符替换5、检测字母或数字6、纠正字母7、输出英文中所有长度为3个字母的单词 1、输出随机字符串 编写程序,输出由英文字母大小写或…...
Transmit :macOS 好用的 Ftp/SFtp 工具
Transmit 是一种功能强大的 FTP/SFTP/WebDAV 客户端软件,是一个 Mac OS X 平台上设计的文件传输软件。它由 Panic(一家以软件工具为主的公司)开发和维护,是一款非常受欢迎且易于使用的软件,而且被广泛认为是 Mac OS X …...

【Github】git clone命令下载文件中途停止
方法一: 使用git clone命令下载github上的源代码时,有时文件下载到一定百分比时就停止不动, 这是因为我们所下载的文件很大,超过了git预先分配的Postbuffer容量,所以一直卡在那里。可以使用以下命令查看当前Postbuffe…...

Clickhouse学习笔记(10)—— 查询优化
单表查询 Prewhere 替代 where prewhere与where相比,在过滤数据的时候会首先读取指定的列数据,来判断数据过滤,等待数据过滤之后再读取 select 声明的列字段来补全其余属性 简单来说就是先过滤再查询,而where过滤是先查询出对应…...

[量化投资-学习笔记012]Python+TDengine从零开始搭建量化分析平台-策略回测
上一章节《MACD金死叉策略回测》中,对平安银行这只股票,按照金死叉策略进行了回测。 但通常我们的股票池中有许多股票,每完成一个交易策略都需要对整个股票池进行回测。 下面使用简单的轮询,对整个股票池进行回测。 # 计算单只…...

MySQL 查看 event 执行记录
文章目录 1. 查看 EVENT 执行记录2. 示例3. 结论 MySQL 是一款流行的关系型数据库管理系统,它提供了许多功能来帮助用户管理和操作数据库。其中之一就是 EVENT事件,它允许用户在特定的时间间隔内自动执行指定的操作,类似于计划任务。 在使用 …...
开发知识点-Vue-Electron
Electron ElectronVue打包.exe桌面程序 ElectronVue打包.exe桌面程序 为了不报错 卸载以前的脚手架 npm uninstall -g vue-cli安装最新版脚手架 cnpm install -g vue/cli创建一个 vue 随便起个名 vue create electron-vue-example (随便起个名字electron-vue-example)进入 创建…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...
