【Linux】编译Linux内核
之所以编译内核,是因为gem5全系统仿真需要vmlinux文件,在此记录一下以备后面需要。
此过程编译之后会获得vmlinux和bzImage两个文件;
主要参考知行大佬的编译内核与gem5官方教程
文章目录
- 一、Linux源码下载
- 二、安装编译依赖
- 三、编译
- 1. 内核编译前配置
- 2. 进行编译:
- 3. 编译失败进行清除重试
- 四、可能遇到的问题
- 错误1
- 错误2
- 错误3
一、Linux源码下载
注意:内核编译一般需要20GB左右的空间,可以预留相应的空间,之后的源码和编译过程都在那里进行。
Linux Kernel包含了所有Linux内核的版本,可以挑选自己需要的内核版本下载即可,本文以5.4.49为例,可以使用wget下载:
wget https://mirrors.edge.kernel.org/pub/linux/kernel/v5.x/linux-5.4.49.tar.gz
tar xf linux-5.4.49.tar.gz
cd linux-5.4.49
wget有可能比较慢,此时也可以直接点进上面的Linux Kernel页面手动下载并解压到指定位置。
二、安装编译依赖
一般来说,需要下面的依赖库,直接安装就可以:
sudo apt update
sudo apt-get install git fakeroot build-essential ncurses-dev xz-utils libssl-dev bc flex libelf-dev bison vim
三、编译
1. 内核编译前配置
编译内核前需要进行编译配置,选择哪些组件要编译进去,添加调试信息等。内核中包含了大量的驱动代码,很多驱动其实用不到,一般是通过一个图形化界面选择配置。
在linux-5.4.49文件夹下面打开终端输入:
make menuconfig
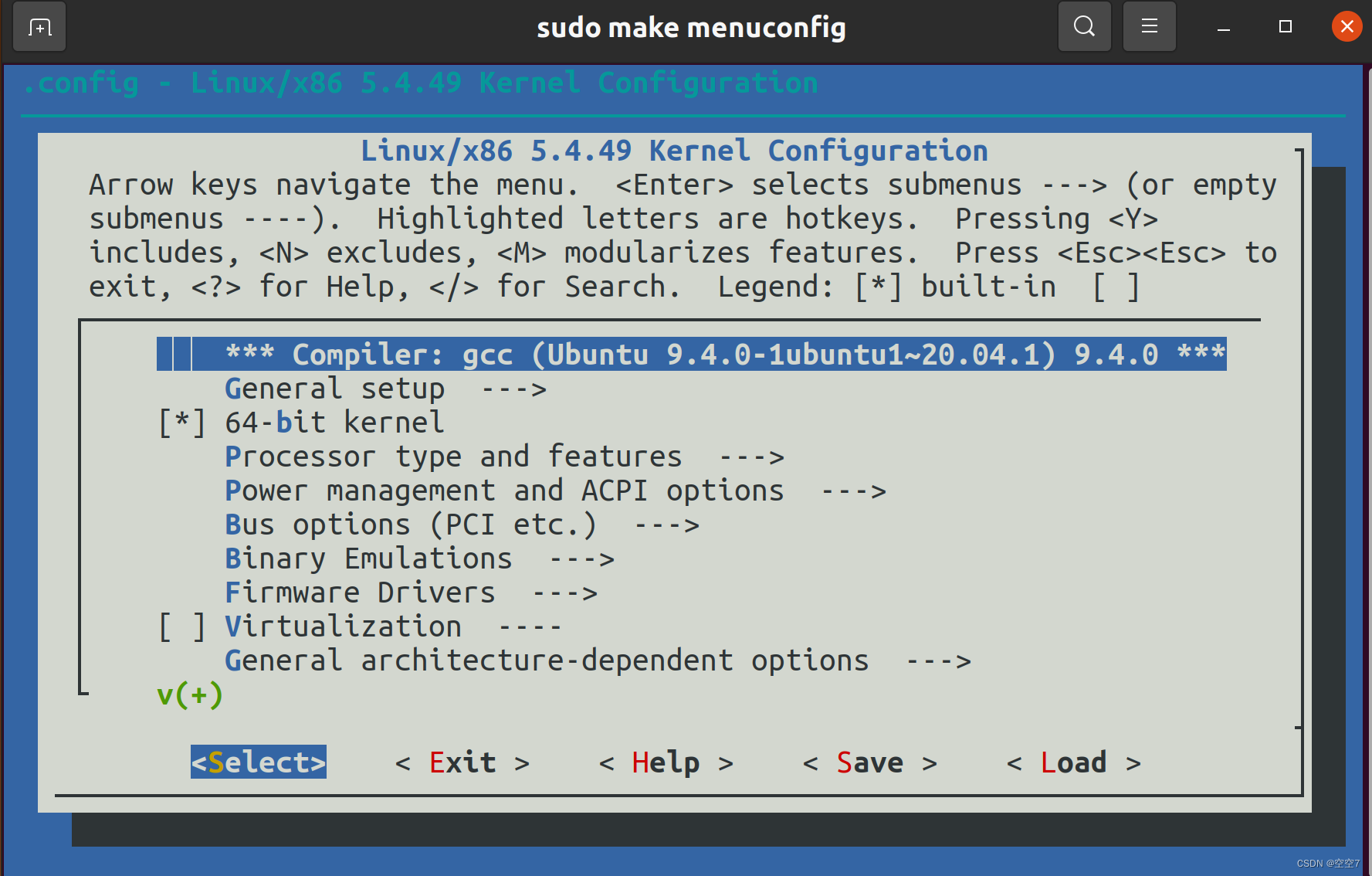
在这个界面通过方向键和上边提示的字母选项进行配置,*代表已选择。具体配置可以参考编译内核或者按需选择其他教程。
配置完毕选择Save然后Exit退出,会生成一个.config文件,这个文件里面就包含了编译配置信息,所以,需要再修改配置信息,可以用vscode打开.config文件直接进行修改。
作为普通人的我们,不大清楚哪些需要哪些不需要,我选择使用gem5官方提供的.config文件,将这个文件下载下来替换原本.config内容即可。
注意,.config文件是隐藏文件,需要选择文件夹的显示隐藏文件才能看到。
2. 进行编译:
sudo make -j 24
# 后面的数字是同时进行编译的线程数,可以灵活根据电脑配置选择
编译时间长短不定,取决于配置信息和线程数。使用gem5官方的配置文件我大概编译了几分钟就结束,得到的vmlinux文件只有26MB,但是自己通过图形化界面配置,编译则需要半个小时左右,得到的vmlinux文件有500MB。看来还是包含了很多不必要的东西。
编译得到的文件有:./vmlinux 和 ./arch/x86/boot/bzImage,参考知行大佬的解释:
vmlinux和bzImage都是Linux内核编译生成的可执行文件,它们的主要区别在于它们的文件格式和用途。
- vmlinux是Linux内核编译生成的未压缩的内核镜像文件,它包含了整个内核的代码和数据,可以用来调试内核.它通常比较大,因为它没有被压缩.
- bzImage是Linux内核编译生成的压缩内核镜像文件,它是用来引导启动Linux操作系统的.它是通过将vmlinux压缩成一个单独的文件,并添加一些引导代码和头部信息来生成的.
当系统引导时,bzImage首先会被加载到内存中,然后被解压缩成vmlinux形式的内核映像.因为vmlinux文件比较大,而且内核启动过程中需要加载和解压缩文件,所以bzImage文件通常比vmlinux文件小很多.
3. 编译失败进行清除重试
如果编译失败,使用下面命令清除重试:
sudo make mrproper
sudo make clean
四、可能遇到的问题
正常流程下来,极有可能遇到下面的问题:
错误1
make[1]: *** No rule to make target 'debian/canonical-certs.pem', needed by 'certs/x509_certificate_list'. Stop.
make: *** [Makefile:1868: certs] Error 2
在终端中执行:
scripts/config --disable SYSTEM_TRUSTED_KEYS
错误2
make[1]: *** No rule to make target 'debian/canonical-revoked-certs.pem', needed by 'certs/x509_revocation_list'. Stop.
make: *** [Makefile:1868: certs] Error 2
在终端中执行:
scripts/config --disable SYSTEM_REVOCATION_KEYS
错误3
BTF: .tmp_vmlinux.btf: pahole version v1.15 is too old, need at least v1.16
Failed to generate BTF for vmlinux
Try to disable CONFIG_DEBUG_INFO_BTF
make: *** [Makefile:1199: vmlinux] Error 1
打开.config文件注释CONFIG_DEBUG_INFO_BTF
**注意:**建议遇到之后直接使用上面的清除命令,重新生成.config文件,提前将需要注释和取消的选项进行处理。随后进行编译,会询问你是否需要开启上面注释的选项,全部按Enter默认就可以,不要选择Y或N。
报错参考1
报错参考2
相关文章:

【Linux】编译Linux内核
之所以编译内核,是因为gem5全系统仿真需要vmlinux文件,在此记录一下以备后面需要。 此过程编译之后会获得vmlinux和bzImage两个文件; 主要参考知行大佬的编译内核与gem5官方教程 文章目录 一、Linux源码下载二、安装编译依赖三、编译1. 内核编…...
网页判断版本更新
一、需求解析 为什么我会想到这个技术呢,是因为我有一次发现,我司的用户在使用网页的时候,经常会出现一个页面放很久,下班也不关这个页面,这样就会导致页面的代码长时间处于不更新的状态。 在使用到一个功能出了bug&a…...
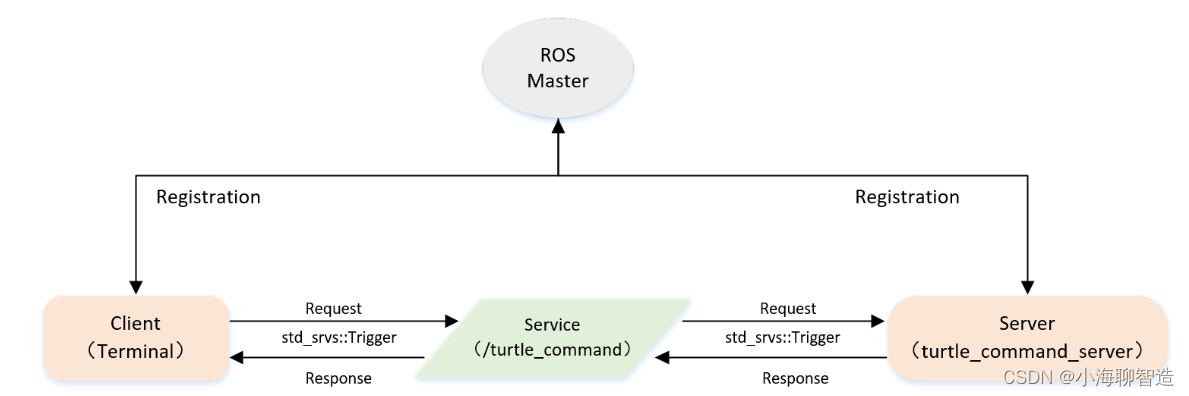
ros1 基础学习08- 实现Server端自定义四 Topic模式控制海龟运动
一、服务模型 Server端本身是进行模拟海龟运动的命令端,它的实现是通过给海龟发送速度(Twist)的指令,来控制海龟运动(本身通过Topic实现)。 Client端相当于海龟运动的开关,其发布Request来控制…...

面试题之TCP粘包现象及其解决方法
计算机网络每层的基本单位:物理层(第一层):比特流;数据链路层(第二层):数据帧;网络层(第三层):数据包;传输层(…...
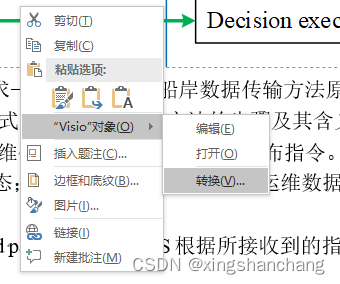
Word 插入的 Visio 图片显示为{EMBED Visio.Drawing.11} 解决方案
World中,如果我们插入了Visio图还用了Endnote, 就可能出现:{EMBED Visio.Drawing.11}问题 解决方案: 1.在相应的文字上右击,在出现的快捷菜单中单击“切换域代码”,一个一个的修复。 2.在菜单工具–>…...

Elasticsearch倒排索引、索引操作、映射管理
一、倒排索引 1、倒排索引是什么 倒排索引源于实际应用中需要根据属性的值来查找记录,这种索引表中的每一个项都包括一个属性值和具有该属性值的各记录的地址。由于不是由记录来确定属性值,而是由属性值来确定记录的位置,因而成为倒排索引。带有倒排索引的文件我们称之为倒…...

USEFUL PHRASES
THINGS YOU LIKE Q:Do you like social science? Yes, I can’t get enough of it.Yes, what I like most about it is it’s so interesting, for example, last week I read an article about solar panels and how we use them to protect the planet.Yes, I lo…...
与 HoughLinesP()对比)
【OpenCV】 拟合直线 与 霍夫直线 对比 , fitLine()与 HoughLinesP()对比
文章目录 1 fitLine 与 HoughLinesP 函数原型2 拟合直线 与 霍夫直线 对比拟合线和圆,是通过已知点拟合出对应的方程,拟合方法如最小二乘法,RANSAC算法等。如果拟合点的离散成都较高,拟合方法的正确选择,是提高识别精度的一大要点。 1 fitLine 与 HoughLinesP 函数原型 …...
查找和修复数据源)
Python与ArcGIS系列(六)查找和修复数据源
目录 0 简述1 查找丢失数据源2 findAndReplaceWorkspacePaths()方法修复丢失数据源3 replaceWorkspaces()方法修复丢失数据源4 replaceDataSource()修复单个图层和表对象0 简述 当对数据源进行移动、转换和删除时都会导致数据源丢失链接问题,无法正常显示地图数据。对于多个数…...

聊聊logback的TimeBasedRollingPolicy
序 本文主要研究一下logback的TimeBasedRollingPolicy TimeBasedRollingPolicy public class TimeBasedRollingPolicy<E> extends RollingPolicyBase implements TriggeringPolicy<E> {static final String FNP_NOT_SET "The FileNamePattern option must…...
numpy 基础使用
NumPy是Python中科学计算的基础包。它是一个Python库,提供多维数组对象,各种派生对象(如掩码数组和矩阵),以及用于数组快速操作的各种API,有包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变…...

sqlite3编译脚本
../configure --hostarm --buildx86 CC/opt/sdk/gcc-arm-8.3-arm-armv5t-linux-gnueabi/bin/arm-armv5t-linux-gnueabi-gcc --prefix/opt/sdk/gcc-arm-8.3-arm-armv5t-linux-gnueabi/arm-armv5t-linux-gnueabi/sysroot/usr...
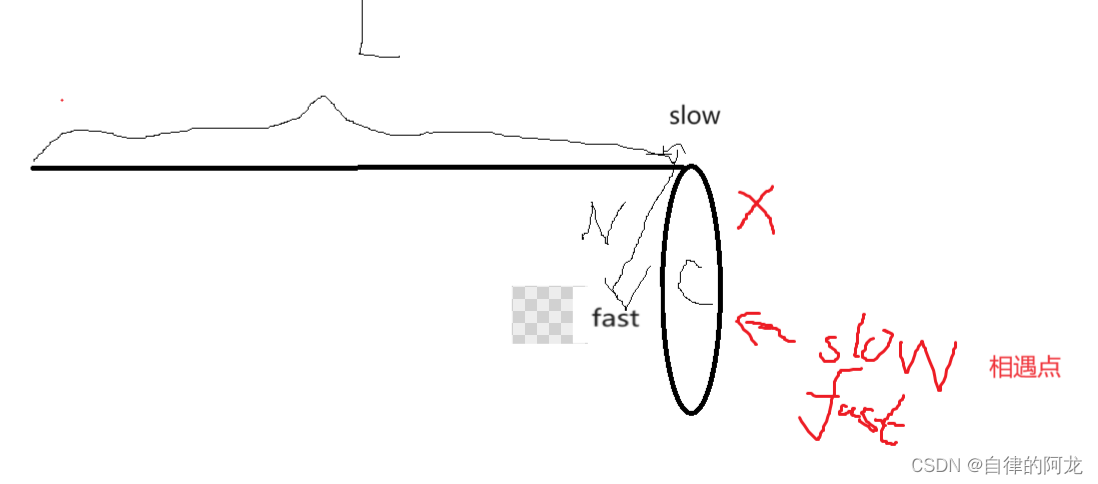
环形链表解析(c语言)c语言版本!自我解析(看了必会)
目录 1.判断一个表是否是环形链表! 代码如下 解析如下 2.快指针的步数和慢指针的步数有什么影响(无图解析) 3.怎么找到环形链表的入环点 代码如下 解析如下 1.判断一个表是否是环形链表! 代码如下 bool hasCycle(struct L…...

科技云报道:数智化升级,如何跨越数字世界与实体产业的鸿沟?
科技云报道原创。 数智化是当下商业环境下最大的确定性。 2022年,中国数字经济规模达50.2万亿元,占国内生产总值比重提升至41.5%,数字经济成为推动经济发展的重要引擎。从小型创业公司到跨国巨头,数字化转型在企业发展历程中彰显…...
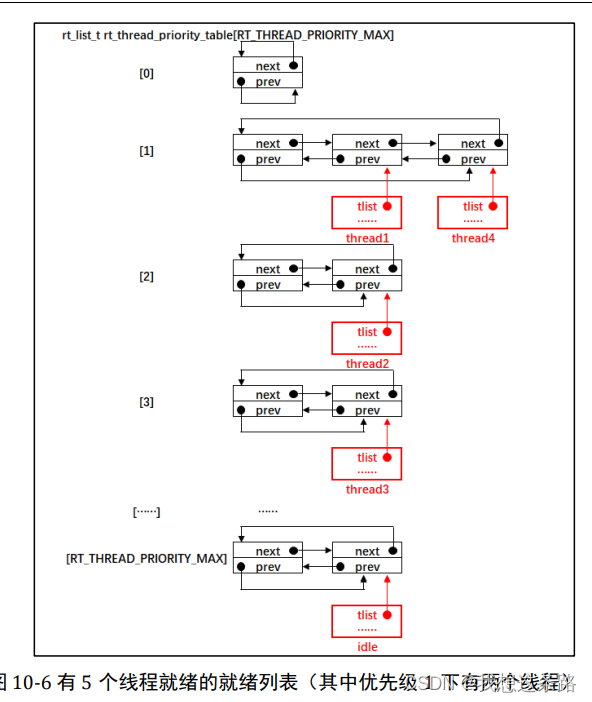
Rt-Thread 移植6--多线程(KF32)
6.1 就绪列表 6.1.1 线程就绪优先级组 线程优先级表的索引对应的线程的优先级。 为了快速的找到线程在线程优先级表的插入和移出的位置,RT-Thread专门设计了一个线程就绪优先级组。线程就绪优先组是一个32位的整型数,每一个位对应一个优先级ÿ…...

HarmonyOS应用开发-首选项与后台通知管理
首选项 在移动互联网蓬勃发展的今天,移动应用给我们生活带来了极大的便利,这些便利的本质在于数据的互联互通。因此在应用的开发中数据存储占据了非常重要的位置,HarmonyOS应用开发也不例外。本章以HarmonyOS的首选项为例,介绍了…...
通过easyexcel导出数据到excel表格
这篇文章简单介绍一下怎么通过easyexcel做数据的导出,使用之前easyui构建的歌曲列表crud应用,添加一个导出按钮,点击的时候直接连接后端接口地址,在后端的接口完成数据的导出功能。 前端页面完整代码 let editingId; let request…...
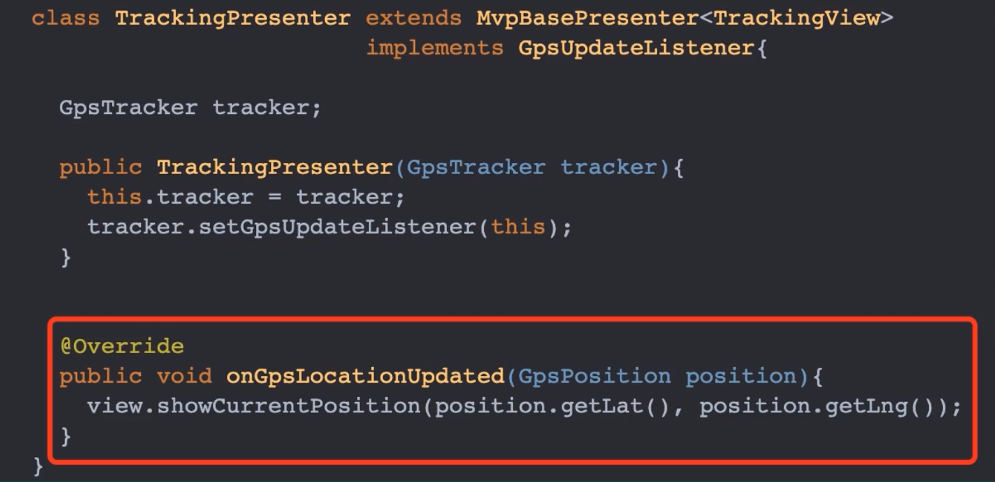
Android---MVP 中 presenter 声明周期的管理
我们经常在 Android MVP 架构中的 Presenter 层做一些耗时操作,比如请求网络数据,然后根据请求后的结果刷新 View。但是,如果按返回结束 Activity,而 Presenter 依然在执行耗时操作。那么就有可能造成内存泄漏,严重时甚…...

Oracle中的索引碎片
索引碎片是指索引在存储空间上不连续的分布情况,它可能会影响到数据库性能和查询效率。索引碎片化主要由以下几个原因导致: 插入、更新和删除操作:当对表中的数据进行插入、更新或删除操作时,索引也需要相应地更新。这些DML操作可…...
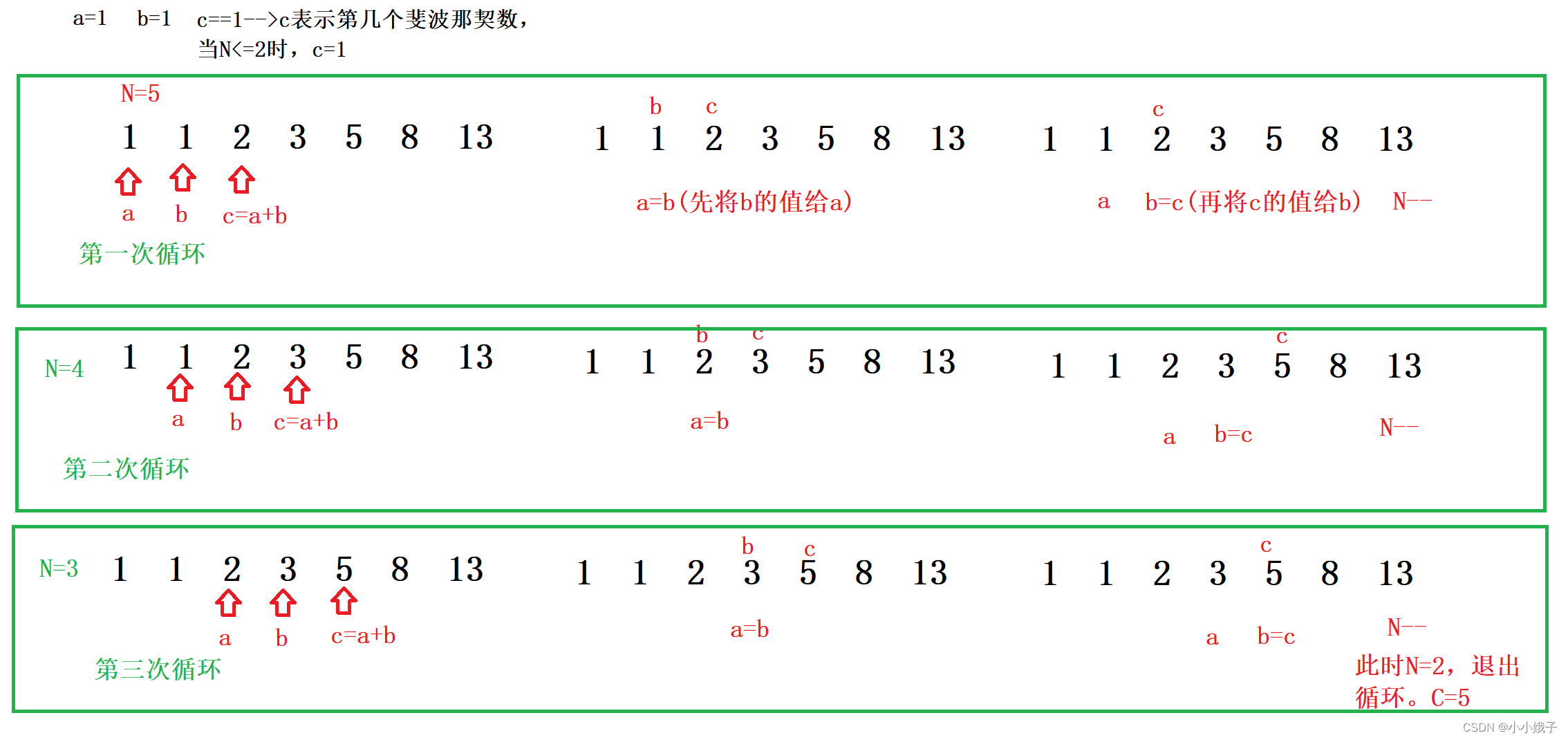
Java必刷入门递归题×5(内附详细递归解析图)
目录 1.求N的阶乘 2.求12...N的和 3.顺序打印数字的每一位 4.求数字的每一位之和 5.求斐波拉契数列 1.求N的阶乘 (1)解析题目意思 比如求5的阶乘,符号表示就是5!;所以5!5*4*3*2*1我们下面使用简单的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
