如何判断从本机上传到服务器的文件数据内容是一致的?用md5加密算法!
问题场景
最近在帮导师做横向,我想把整个项目环境放到服务器中,需要把一个很大的数据文件传到服务器,传上去很方便,但是涉及到文件的压缩上传和服务器内解压环节,不是太确定文件在本机和服务器的数据内容是否一致。
解决思路
可以利用md5算法,全称是Message-Digest Algorithm 5,即信息摘要算法。
md5算法有以下特点:
- 压缩性:任意长度的数据,算出的MD5值长度都是固定的。
- 容易计算:从原数据计算出MD5值很容易。
- 抗修改性:对原数据进行任何改动,哪怕只修改1个字节,所得到的MD5值都有很大区别。
- 强抗碰撞:已知原数据和其MD5值,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
实现步骤
假定本机是windows环境,服务器为linux环境。
- 在本机上打开powershell( 一定得是powershell打开,不能是简单的cmd)
- 到需要检验是否一致的文件所在目录
- 输入
GetFile-Hash+ 文件名,得到md5算法加密后的序列

- 在服务器上,到需要检验是否一致的文件所在目录
- 输入
sha256sum+ 文件名,得到md5算法加密后的序列

- 对比本机和服务器上得到的md5加密序列,如果一模一样(忽略大小写),则数据内容是一致的,如果有任何地方存在不一样的,则数据内容不完全一致。
相关文章:

如何判断从本机上传到服务器的文件数据内容是一致的?用md5加密算法!
问题场景 最近在帮导师做横向,我想把整个项目环境放到服务器中,需要把一个很大的数据文件传到服务器,传上去很方便,但是涉及到文件的压缩上传和服务器内解压环节,不是太确定文件在本机和服务器的数据内容是否一致。 解…...

Ubuntu 20.04 DNS解析原理, 解决resolv.conf被覆盖问题
------------------------------------------------------------------ author: hjjdebug date: 2023年 11月 09日 星期四 14:01:11 CST description: Ubuntu 20.04 DNS解析原理, 解决resolv.conf被覆盖问题 ----------------------------------------------------------------…...
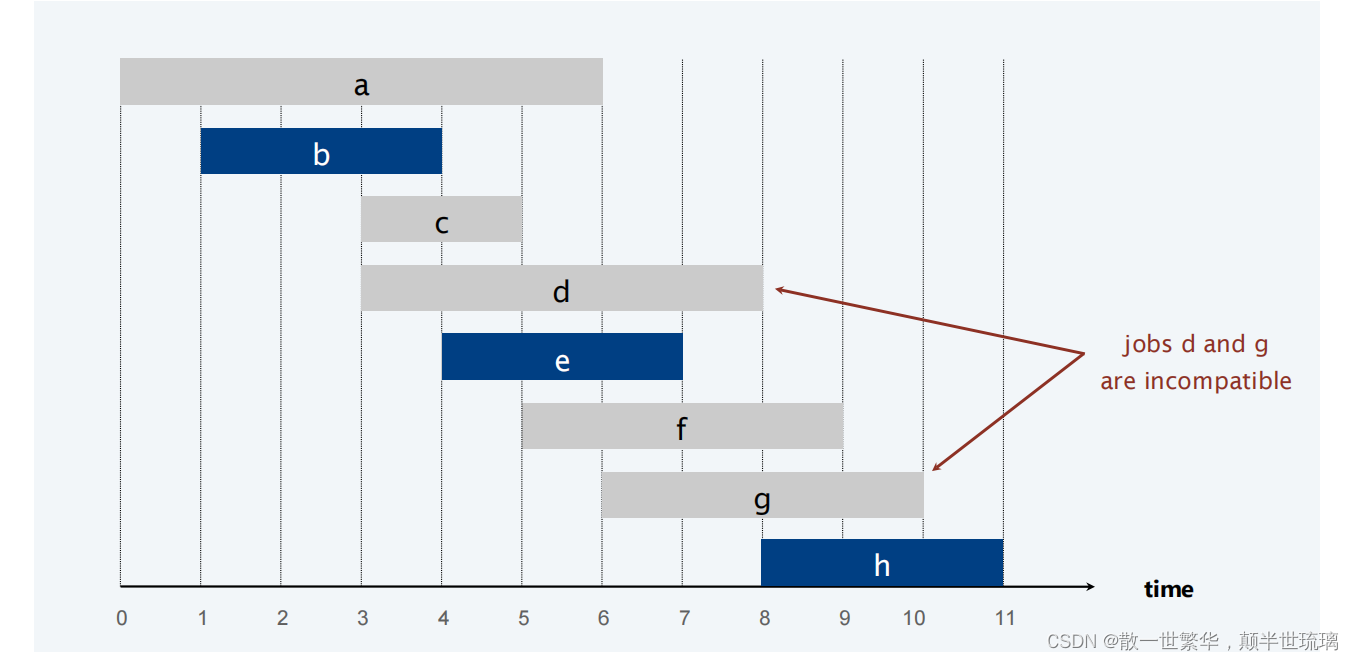
探索经典算法:贪心、分治、动态规划等
1.贪心算法 贪心算法是一种常见的算法范式,通常在解决最优化问题中使用。 贪心算法是一种在每一步选择中都采取当前状态下最优决策的算法范式。其核心思想是选择每一步的最佳解决方案,以期望达到最终的全局最优解。这种算法特点在于只考虑局部最优解&am…...
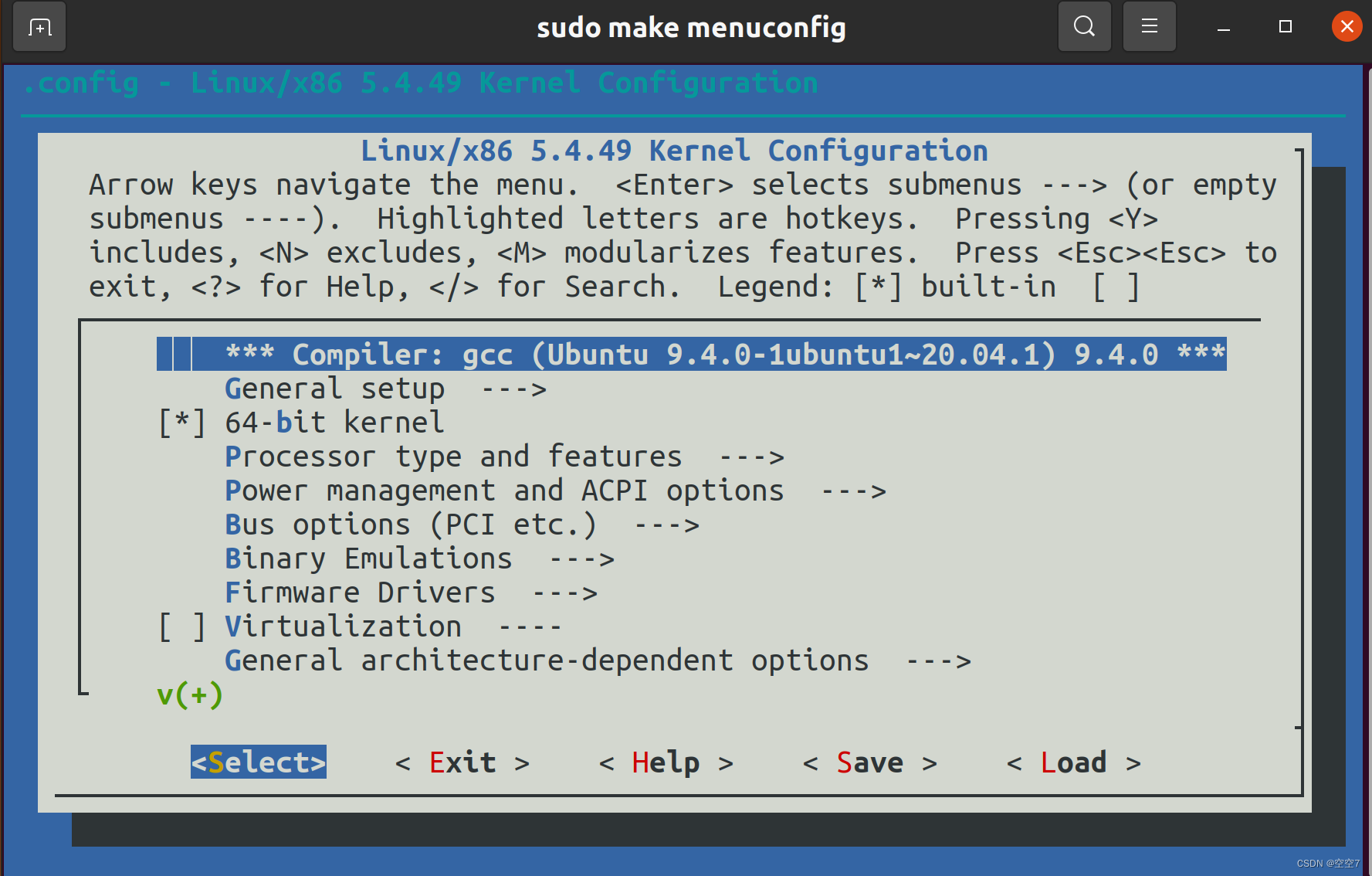
【Linux】编译Linux内核
之所以编译内核,是因为gem5全系统仿真需要vmlinux文件,在此记录一下以备后面需要。 此过程编译之后会获得vmlinux和bzImage两个文件; 主要参考知行大佬的编译内核与gem5官方教程 文章目录 一、Linux源码下载二、安装编译依赖三、编译1. 内核编…...
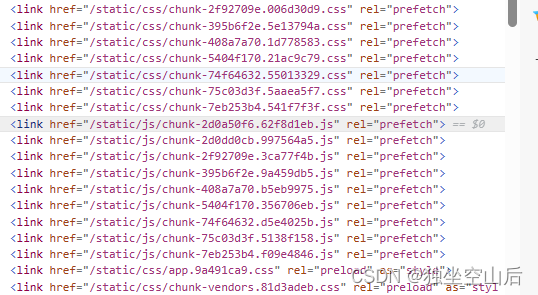
网页判断版本更新
一、需求解析 为什么我会想到这个技术呢,是因为我有一次发现,我司的用户在使用网页的时候,经常会出现一个页面放很久,下班也不关这个页面,这样就会导致页面的代码长时间处于不更新的状态。 在使用到一个功能出了bug&a…...
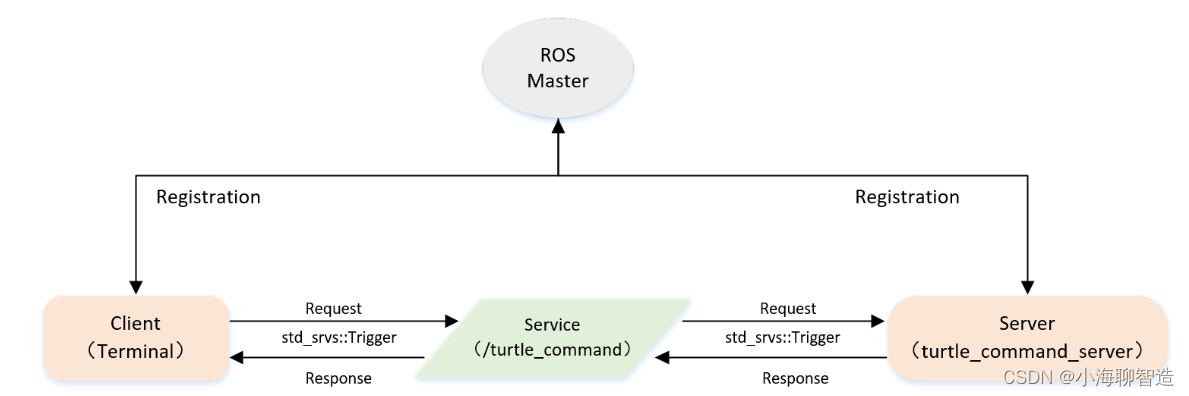
ros1 基础学习08- 实现Server端自定义四 Topic模式控制海龟运动
一、服务模型 Server端本身是进行模拟海龟运动的命令端,它的实现是通过给海龟发送速度(Twist)的指令,来控制海龟运动(本身通过Topic实现)。 Client端相当于海龟运动的开关,其发布Request来控制…...

面试题之TCP粘包现象及其解决方法
计算机网络每层的基本单位:物理层(第一层):比特流;数据链路层(第二层):数据帧;网络层(第三层):数据包;传输层(…...
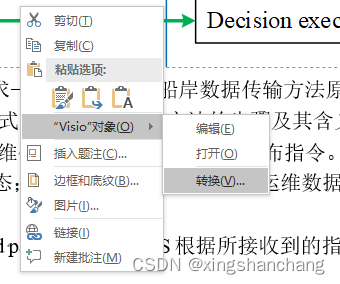
Word 插入的 Visio 图片显示为{EMBED Visio.Drawing.11} 解决方案
World中,如果我们插入了Visio图还用了Endnote, 就可能出现:{EMBED Visio.Drawing.11}问题 解决方案: 1.在相应的文字上右击,在出现的快捷菜单中单击“切换域代码”,一个一个的修复。 2.在菜单工具–>…...

Elasticsearch倒排索引、索引操作、映射管理
一、倒排索引 1、倒排索引是什么 倒排索引源于实际应用中需要根据属性的值来查找记录,这种索引表中的每一个项都包括一个属性值和具有该属性值的各记录的地址。由于不是由记录来确定属性值,而是由属性值来确定记录的位置,因而成为倒排索引。带有倒排索引的文件我们称之为倒…...

USEFUL PHRASES
THINGS YOU LIKE Q:Do you like social science? Yes, I can’t get enough of it.Yes, what I like most about it is it’s so interesting, for example, last week I read an article about solar panels and how we use them to protect the planet.Yes, I lo…...
与 HoughLinesP()对比)
【OpenCV】 拟合直线 与 霍夫直线 对比 , fitLine()与 HoughLinesP()对比
文章目录 1 fitLine 与 HoughLinesP 函数原型2 拟合直线 与 霍夫直线 对比拟合线和圆,是通过已知点拟合出对应的方程,拟合方法如最小二乘法,RANSAC算法等。如果拟合点的离散成都较高,拟合方法的正确选择,是提高识别精度的一大要点。 1 fitLine 与 HoughLinesP 函数原型 …...
查找和修复数据源)
Python与ArcGIS系列(六)查找和修复数据源
目录 0 简述1 查找丢失数据源2 findAndReplaceWorkspacePaths()方法修复丢失数据源3 replaceWorkspaces()方法修复丢失数据源4 replaceDataSource()修复单个图层和表对象0 简述 当对数据源进行移动、转换和删除时都会导致数据源丢失链接问题,无法正常显示地图数据。对于多个数…...

聊聊logback的TimeBasedRollingPolicy
序 本文主要研究一下logback的TimeBasedRollingPolicy TimeBasedRollingPolicy public class TimeBasedRollingPolicy<E> extends RollingPolicyBase implements TriggeringPolicy<E> {static final String FNP_NOT_SET "The FileNamePattern option must…...
numpy 基础使用
NumPy是Python中科学计算的基础包。它是一个Python库,提供多维数组对象,各种派生对象(如掩码数组和矩阵),以及用于数组快速操作的各种API,有包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变…...

sqlite3编译脚本
../configure --hostarm --buildx86 CC/opt/sdk/gcc-arm-8.3-arm-armv5t-linux-gnueabi/bin/arm-armv5t-linux-gnueabi-gcc --prefix/opt/sdk/gcc-arm-8.3-arm-armv5t-linux-gnueabi/arm-armv5t-linux-gnueabi/sysroot/usr...
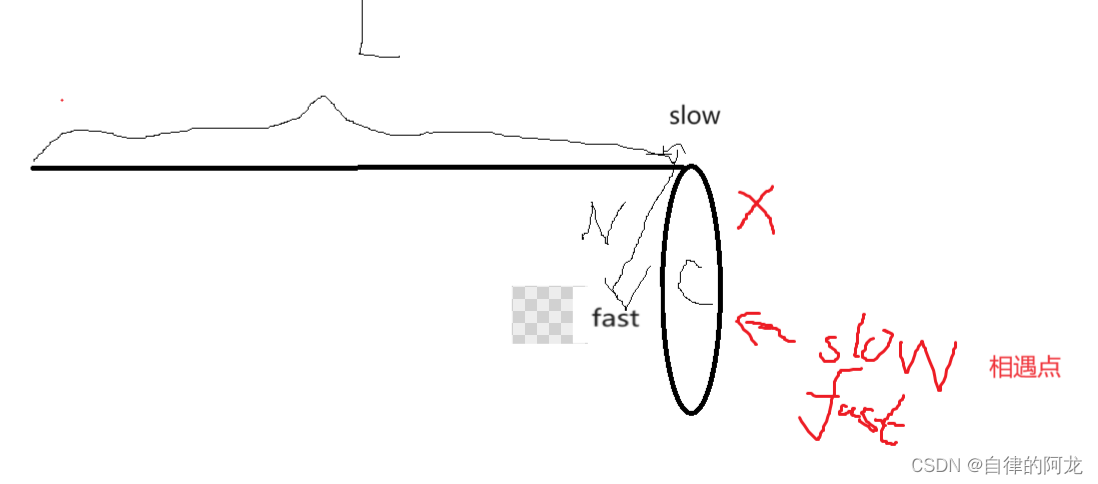
环形链表解析(c语言)c语言版本!自我解析(看了必会)
目录 1.判断一个表是否是环形链表! 代码如下 解析如下 2.快指针的步数和慢指针的步数有什么影响(无图解析) 3.怎么找到环形链表的入环点 代码如下 解析如下 1.判断一个表是否是环形链表! 代码如下 bool hasCycle(struct L…...

科技云报道:数智化升级,如何跨越数字世界与实体产业的鸿沟?
科技云报道原创。 数智化是当下商业环境下最大的确定性。 2022年,中国数字经济规模达50.2万亿元,占国内生产总值比重提升至41.5%,数字经济成为推动经济发展的重要引擎。从小型创业公司到跨国巨头,数字化转型在企业发展历程中彰显…...
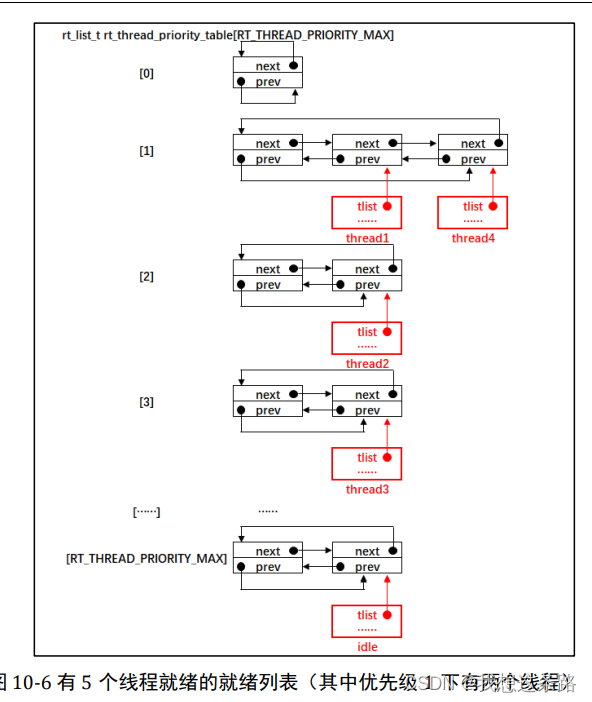
Rt-Thread 移植6--多线程(KF32)
6.1 就绪列表 6.1.1 线程就绪优先级组 线程优先级表的索引对应的线程的优先级。 为了快速的找到线程在线程优先级表的插入和移出的位置,RT-Thread专门设计了一个线程就绪优先级组。线程就绪优先组是一个32位的整型数,每一个位对应一个优先级ÿ…...

HarmonyOS应用开发-首选项与后台通知管理
首选项 在移动互联网蓬勃发展的今天,移动应用给我们生活带来了极大的便利,这些便利的本质在于数据的互联互通。因此在应用的开发中数据存储占据了非常重要的位置,HarmonyOS应用开发也不例外。本章以HarmonyOS的首选项为例,介绍了…...
通过easyexcel导出数据到excel表格
这篇文章简单介绍一下怎么通过easyexcel做数据的导出,使用之前easyui构建的歌曲列表crud应用,添加一个导出按钮,点击的时候直接连接后端接口地址,在后端的接口完成数据的导出功能。 前端页面完整代码 let editingId; let request…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
