三国杀中的概率学问题3——王荣
前言
本文是三国杀中的概率学问题系列文章中的一篇,将详细讨论王荣吉占的期望摸牌数问题。并加上连续情形作为拓展。
值得说明的是,本文的思路受到了一篇文章的启发,在此特别鸣谢,这是文章的链接。
王荣吉占的期望摸牌数

王荣的二技能吉占很有意思,展示牌堆顶的一张牌,然后猜测下一张牌比这张牌大还是比这张牌小,猜对了就继续猜,直到猜错为止,然后最终可以获得展示的所有牌。所以即便第一次就猜错,也能拿到2张牌(第一张展示的牌,和猜错的这张牌)。为了能够摸更多的牌,我们需要采取贪心的猜牌策略,保证自己这次猜对的概率最大。也就是说,在展示的牌为1-6时,我们选择猜大,8-13时猜小,7的时候由于猜大和猜小的概率一样,所以猜大猜小都可以。
离散情形
为了使得模型更一般化,将13种不同的点数改为n种不同的点数。那么问题可以重新描述如下:
问题:牌有1~n这n种点数,我们先亮出第一张牌,然后猜测下一张牌跟这一张牌的大小关系,然后亮出下一张牌,若猜对则继续猜,猜错就停止。求在最优策略下平均能亮出几张牌。
由于牌堆为理想牌堆,不管怎么拿牌,每种点数的牌的张数都是一样的,所以最优策略即为:若当前牌的点数小于等于 n + 1 2 \frac{n+1}{2} 2n+1,就猜大,否则猜小。
我们令 f ( x ) f(x) f(x)表示当前牌的点数为 x x x时,后面会亮出的牌数的数学期望。那么,我们可以得到下面的公式:
f ( x ) = { ∑ i = x + 1 n 1 n f ( i ) + 1 0 ≤ x ≤ n + 1 2 ∑ i = 1 x − 1 1 n f ( i ) + 1 n + 1 2 < x ≤ 1 f(x)=\begin{cases} \sum_{i=x+1}^n{\frac{1}{n}f(i)+1} &0\leq x\leq\frac{n+1}{2} \\ \sum_{i=1}^{x-1}{\frac{1}{n}f(i)+1} & \frac{n+1}{2}<x\leq 1 \end{cases} f(x)={∑i=x+1nn1f(i)+1∑i=1x−1n1f(i)+10≤x≤2n+12n+1<x≤1
解释一下这个公式,当前牌的点数为 x x x时,首先会亮出下一张牌,这是+1的含义。然后下一张牌是每个点数的概率都是 1 n \frac{1}{n} n1,把猜对了能亮出的牌数乘以概率累加起来,就是猜对了之后期望亮出的牌数。分成两段也仅仅是因为猜测策略的原因。
我们要求的是平均能亮出几张牌,假设这个数量为 E E E,那么 E = 1 n ∑ i = 1 n f ( i ) + 1 E=\frac{1}{n}\sum_{i=1}^n{f(i)}+1 E=n1∑i=1nf(i)+1
首先先亮出一张牌,然后这张牌的点数有n种可能性,即有 1 n \frac{1}{n} n1的概率为i。如果第一张牌是i的话,则期望亮出的牌数就是 f ( i ) f(i) f(i)。于是我们把概率乘以亮出牌数累加起来,就是接下来会亮出的牌数,即 1 n ∑ i = 1 n f ( i ) \frac{1}{n}\sum_{i=1}^n{f(i)} n1∑i=1nf(i)。再加上第一张亮出的牌,就是 1 n ∑ i = 1 n f ( i ) + 1 \frac{1}{n}\sum_{i=1}^n{f(i)}+1 n1∑i=1nf(i)+1了。 E E E就是我们想求的答案。
接下来我们来算出 f ( x ) f(x) f(x)的具体值。
我们设出 f ( x ) f(x) f(x)的前缀和。令 F ( x ) = ∑ i = 1 n f ( i ) F(x)=\sum_{i=1}^n{f(i)} F(x)=∑i=1nf(i)
当 n + 1 2 < x ≤ 1 \frac{n+1}{2}<x\leq 1 2n+1<x≤1时:
f ( x ) = 1 n F ( x − 1 ) + 1 f(x)=\frac{1}{n}F(x-1)+1 f(x)=n1F(x−1)+1
F ( x − 1 ) = n f ( x ) + n F(x-1)=nf(x)+n F(x−1)=nf(x)+n
将 x + 1 x+1 x+1代入 x x x得:
F ( x ) = n f ( x + 1 ) + n F(x)=nf(x+1)+n F(x)=nf(x+1)+n
两式相减得:
f ( x ) = n f ( x + 1 ) − n f ( x ) f(x)=nf(x+1)-nf(x) f(x)=nf(x+1)−nf(x)
于是得到了 f ( x ) f(x) f(x)的递推式
f ( x + 1 ) = n + 1 n f ( x ) f(x+1)=\frac{n+1}{n}f(x) f(x+1)=nn+1f(x)
由于 n n n为常数,于是我们发现在 n + 1 2 < x ≤ 1 \frac{n+1}{2}<x\leq 1 2n+1<x≤1上, f ( x ) f(x) f(x)是等比数列。
类似地,在 0 ≤ x ≤ n + 1 2 0\leq x\leq\frac{n+1}{2} 0≤x≤2n+1上求得 f ( x + 1 ) = n n + 1 f ( x ) f(x+1)=\frac{n}{n+1}f(x) f(x+1)=n+1nf(x)
可以发现, f ( x ) f(x) f(x)是一列以 n + 1 2 \frac{n+1}{2} 2n+1为对称轴,先递减,后递增的两段等比数列,公比分别为 n n + 1 \frac{n}{n+1} n+1n和 n + 1 n \frac{n+1}{n} nn+1。
等比数列的求和公式为 S = a 1 ∗ q n − 1 q − 1 S=a_1*\frac{q^n-1}{q-1} S=a1∗q−1qn−1,现在公比已经知道了,所以要求首项。 f ( n + 1 2 ) f(\frac{n+1}{2}) f(2n+1)位于两段的连接处,可以让它作为两段等比数列的首项。现在我们来求 f ( n + 1 2 ) f(\frac{n+1}{2}) f(2n+1)。
我们不妨假设 n n n为奇数,这样 x = n + 1 2 x=\frac{n+1}{2} x=2n+1在公式的两段上都可以成立。于是有
f ( n + 1 2 ) = ∑ i = n + 3 2 n 1 n f ( i ) + 1 = ∑ i = 1 n − 1 2 1 n f ( i ) + 1 f(\frac{n+1}{2})=\sum_{i=\frac{n+3}{2}}^n{\frac{1}{n}f(i)+1}=\sum_{i=1}^{\frac{n-1}{2}}{\frac{1}{n}f(i)+1} f(2n+1)=∑i=2n+3nn1f(i)+1=∑i=12n−1n1f(i)+1
( 2 + 1 n ) f ( n + 1 2 ) = 1 n F ( n ) + 2 (2+\frac{1}{n})f(\frac{n+1}{2})=\frac{1}{n}F(n)+2 (2+n1)f(2n+1)=n1F(n)+2
f ( n + 1 2 ) = 1 2 n + 1 F ( n ) + 2 n 2 n + 1 f(\frac{n+1}{2})=\frac{1}{2n+1}F(n)+\frac{2n}{2n+1} f(2n+1)=2n+11F(n)+2n+12n
利用 f ( x ) f(x) f(x)的对称性,以及等比数列求和公式,有
F ( n ) = ∑ i = 1 n − 1 2 f ( i ) + ∑ i = n + 1 2 n f ( i ) = ∑ i = n + 3 2 n f ( i ) + ∑ i = n + 1 2 n f ( i ) = n + 1 n f ( n + 1 2 ) ( n + 1 n ) n − 1 2 − 1 n + 1 n − 1 + f ( n + 1 2 ) ( n + 1 n ) n + 1 2 − 1 n + 1 n − 1 = [ 2 n ( n + 1 n ) n + 1 2 − 2 n − 1 ] f ( n + 1 2 ) F(n)=\sum_{i=1}^{\frac{n-1}{2}}{f(i)}+\sum_{i=\frac{n+1}{2}}^n{f(i)}=\sum_{i=\frac{n+3}{2}}^n{f(i)}+\sum_{i=\frac{n+1}{2}}^n{f(i)}=\frac{n+1}{n}f(\frac{n+1}{2})\frac{(\frac{n+1}{n})^{\frac{n-1}{2}}-1}{\frac{n+1}{n}-1}+f(\frac{n+1}{2})\frac{(\frac{n+1}{n})^{\frac{n+1}{2}}-1}{\frac{n+1}{n}-1}=[2n(\frac{n+1}{n})^{\frac{n+1}{2}}-2n-1]f(\frac{n+1}{2}) F(n)=∑i=12n−1f(i)+∑i=2n+1nf(i)=∑i=2n+3nf(i)+∑i=2n+1nf(i)=nn+1f(2n+1)nn+1−1(nn+1)2n−1−1+f(2n+1)nn+1−1(nn+1)2n+1−1=[2n(nn+1)2n+1−2n−1]f(2n+1)
联立两式
{ f ( n + 1 2 ) = 1 2 n + 1 F ( n ) + 2 n 2 n + 1 F ( n ) = [ 2 n ( n + 1 n ) n + 1 2 − 2 n − 1 ] f ( n + 1 2 ) \begin{cases} f(\frac{n+1}{2})=\frac{1}{2n+1}F(n)+\frac{2n}{2n+1}\\ F(n)=[2n(\frac{n+1}{n})^{\frac{n+1}{2}}-2n-1]f(\frac{n+1}{2}) \end{cases} {f(2n+1)=2n+11F(n)+2n+12nF(n)=[2n(nn+1)2n+1−2n−1]f(2n+1)
解得
{ f ( n + 1 2 ) = n 2 n + 1 − n ( n + 1 n ) n + 1 2 F ( n ) = n [ 2 n 2 n + 1 ( n + 1 n ) n + 1 2 − 1 ] 1 − n 2 n + 1 ( n + 1 n ) n + 1 2 \begin{cases} f(\frac{n+1}{2})=\frac{n}{2n+1-n(\frac{n+1}{n})^{\frac{n+1}{2}}}\\ F(n)=\frac{n[\frac{2n}{2n+1}(\frac{n+1}{n})^{\frac{n+1}{2}}-1]}{1-\frac{n}{2n+1}(\frac{n+1}{n})^{\frac{n+1}{2}}} \end{cases} ⎩ ⎨ ⎧f(2n+1)=2n+1−n(nn+1)2n+1nF(n)=1−2n+1n(nn+1)2n+1n[2n+12n(nn+1)2n+1−1]
于是,可以得到
E = ∑ i = 1 n 1 n f ( i ) + 1 = 1 n F ( n ) + 1 = 1 2 n + 1 n ( n n + 1 ) n + 1 2 − 1 E=\sum_{i=1}^{n}\frac{1}{n}f(i)+1=\frac{1}{n}F(n)+1=\frac{1}{\frac{2n+1}{n}(\frac{n}{n+1})^\frac{n+1}{2}-1} E=∑i=1nn1f(i)+1=n1F(n)+1=n2n+1(n+1n)2n+1−11
当 n = 13 n=13 n=13时, E ≈ 4.232 E\approx4.232 E≈4.232
当 n → ∞ n\to\infty n→∞时, l i m n → ∞ E = l i m n → ∞ 1 2 ( 1 − 1 n + 1 ) n + 1 2 − 1 = 1 2 e − 1 2 − 1 ≈ 4.69 lim_{n\to\infty}E=lim_{n\to\infty}\frac{1}{2(1-\frac{1}{n+1})^{\frac{n+1}{2}}-1}=\frac{1}{2e^{-\frac{1}{2}}-1}\approx4.69 limn→∞E=limn→∞2(1−n+11)2n+1−11=2e−21−11≈4.69
至此,原题就解出来了。
连续情形
我们再做一点点扩展,看看在 n n n趋于无穷时的情况。现在我们把问题转化为连续的情况。
问题:在[0,1]区间上的均匀分布总体进行依次采样,约定若采样得到的随机数小于 1 2 \frac{1}{2} 21,则猜测下一次采得的随机数会更大;若采样得到的随机数大于 1 2 \frac{1}{2} 21,则猜测下一次采得的随机数会更小。若猜测正确,则继续猜;若猜测错误,则采样终止。求采样次数的数学期望。
设 f ( x ) f(x) f(x)表示当前点为 x x x时,继续猜测的次数。给出 f ( x ) f(x) f(x)的表达式如下:
f ( x ) = { ∫ x 1 f ( t ) d t + 1 0 ≤ x ≤ 1 2 ∫ 0 x f ( t ) d t + 1 1 2 < x ≤ 1 f(x)=\begin{cases} \int_x^1{f(t)dt}+1 &0\leq x\leq\frac{1}{2} \\ \int_0^x{f(t)dt}+1 & \frac{1}{2}<x\leq 1 \end{cases} f(x)={∫x1f(t)dt+1∫0xf(t)dt+10≤x≤2121<x≤1
值得说明的是, x = 1 2 x=\frac{1}{2} x=21的情况对于两个公式都成立。这个式子是怎么得出来的呢?现在的点是 x x x,我们先要按上述规则进行一次猜测(这是+1的含义)。如果猜错了,我们就失去了继续猜测的机会。如果猜对了,那么我们可以继续猜测。假设下一个点是 t t t,这样的概率为 d t dt dt,继续猜测的次数为 f ( t ) f(t) f(t)。这样做一个积分(可以理解为加权平均)就能得到 f ( x ) f(x) f(x)的表达式了。
假设 E E E为采样次数的数学期望,那么 E = ∫ 0 1 f ( t ) d t + 1 E=\int_0^1{f(t)dt}+1 E=∫01f(t)dt+1
这个式子的含义是,先随机出现一个点(这是+1的含义),再按照这个点的值进行加权平均(也就是积分的含义)。
E E E就是在连续情形下,王荣的摸牌数。
接下来,我们开始解这个函数。
首先,发现一个很简单的事实, f ( 0 ) = f ( 1 ) = E f(0)=f(1)=E f(0)=f(1)=E
显然,这个函数关于 x = 1 2 x=\frac{1}{2} x=21是对称的。那么,我们来求一下 f ( 1 2 ) f(\frac{1}{2}) f(21)的值。
f ( 1 2 ) = ∫ 1 2 1 f ( t ) d t + 1 = ∫ 0 1 2 f ( t ) d t + 1 f(\frac{1}{2})=\int_\frac{1}{2}^1{f(t)dt}+1=\int_0^\frac{1}{2}{f(t)dt}+1 f(21)=∫211f(t)dt+1=∫021f(t)dt+1
2 f ( 1 2 ) = ∫ 0 1 f ( t ) d t + 2 = E + 2 2f(\frac{1}{2})=\int_0^1{f(t)dt}+2=E+2 2f(21)=∫01f(t)dt+2=E+2
f ( 1 2 ) = 1 2 E + 1 2 f(\frac{1}{2})=\frac{1}{2}E+\frac{1}{2} f(21)=21E+21
当 0 ≤ x ≤ 1 2 0\leq x\leq \frac{1}{2} 0≤x≤21时,我们对 f ( x ) = ∫ x 1 f ( t ) d t + 1 f(x)=\int_x^1{f(t)dt}+1 f(x)=∫x1f(t)dt+1两边求导,得
f ′ = − f f'=-f f′=−f
这是一个比较简单的常微分方程,接下来需要一点点常微分方程的知识。
d f d x = − f \frac{df}{dx}=-f dxdf=−f
d f f = − d x \frac{df}{f}=-dx fdf=−dx
d l n f = − d x dlnf=-dx dlnf=−dx
l n f = − x + C 1 lnf=-x+C_1 lnf=−x+C1
f = e − x + C 1 = C e − x f=e^{-x+C_1}=Ce^{-x} f=e−x+C1=Ce−x
于是我们解得 f = C e − x f=Ce^{-x} f=Ce−x
代入 x = 0 x=0 x=0和 x = 1 2 x=\frac{1}{2} x=21得
{ C e 0 = E C e − 1 2 = 1 2 E + 1 2 \begin{cases} Ce^0=E \\ Ce^{-\frac{1}{2}}=\frac{1}{2}E+\frac{1}{2} \end{cases} {Ce0=ECe−21=21E+21
解得 C = E = 1 2 e − 1 2 − 1 C=E=\frac{1}{2e^{-\frac{1}{2}}-1} C=E=2e−21−11
于是得到,当 0 ≤ x ≤ 1 2 0\leq x\leq \frac{1}{2} 0≤x≤21时, f ( x ) = e − x 2 e − 1 2 − 1 f(x)=\frac{e^{-x}}{2e^{-\frac{1}{2}}-1} f(x)=2e−21−1e−x
由于 f ( x ) f(x) f(x)关于 x = 1 2 x=\frac{1}{2} x=21对称,可对称地写出 1 2 < x ≤ 1 \frac{1}{2}<x\leq 1 21<x≤1的情况。于是我们可以得到 f ( x ) f(x) f(x)的表达式。
f ( x ) = { e − x 2 e − 1 2 − 1 0 ≤ x ≤ 1 2 e x − 1 2 e − 1 2 − 1 1 2 < x ≤ 1 f(x)=\begin{cases} \frac{e^{-x}}{2e^{-\frac{1}{2}}-1} &0\leq x\leq\frac{1}{2} \\ \frac{e^{x-1}}{2e^{-\frac{1}{2}}-1} & \frac{1}{2}<x\leq 1 \end{cases} f(x)=⎩ ⎨ ⎧2e−21−1e−x2e−21−1ex−10≤x≤2121<x≤1
E = 1 2 e − 1 2 − 1 ≈ 4.69 E=\frac{1}{2e^{-\frac{1}{2}}-1}\approx4.69 E=2e−21−11≈4.69即为我们所求的答案。
可以发现,连续情形就是离散情形在 n → ∞ n\to\infty n→∞时的情况。而指数函数在离散情形下对应的其实就是等比数列。
总结
本文先将问题作为离散情形进行处理,将问题中的n=13推广到了n为任意奇数的情况(偶数情形略有不同,也可以做,但是没有什么意义,笔者就没有单独列出了)。并且将问题推广到了 n n n为 + ∞ +\infty +∞的情形,即连续情形。从而彻底解出了王荣吉占背后的数学模型。
相关文章:

三国杀中的概率学问题3——王荣
前言 本文是三国杀中的概率学问题系列文章中的一篇,将详细讨论王荣吉占的期望摸牌数问题。并加上连续情形作为拓展。 值得说明的是,本文的思路受到了一篇文章的启发,在此特别鸣谢,这是文章的链接。 王荣吉占的期望摸牌数 王荣的…...
Linux - 实现一个简单的 shell
前言 之前我们对进程的替换,进程地址空间等等的概念进行了说明,本篇博客会基于这些知识点来 实现一个简单的 shell ,如有疑问,可以参考下述博客:Linux - 进程程序替换 - C/C 如何实现与各个语言之间的相互调用 - 替换…...
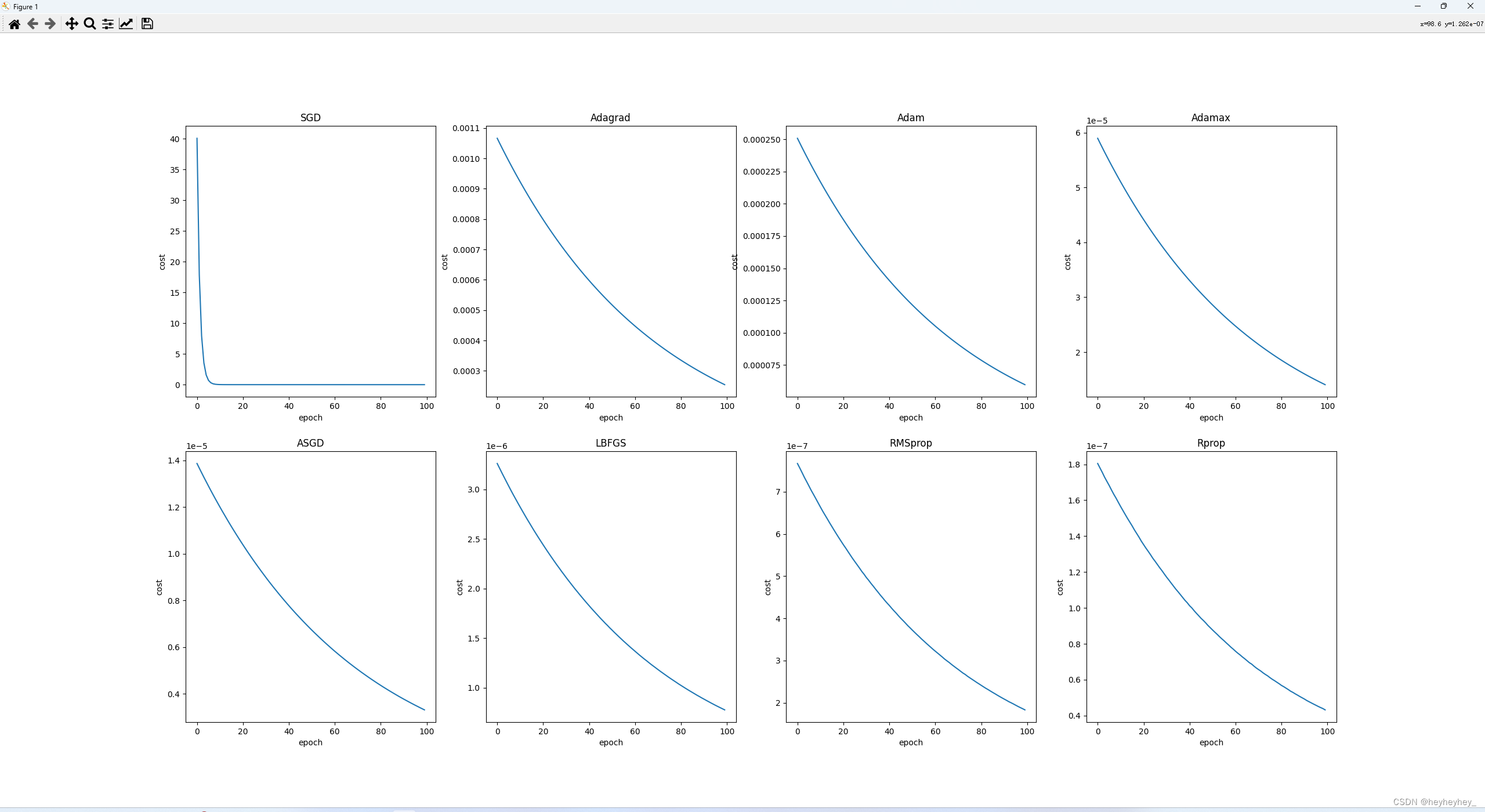
不同优化器的应用
简单用用,优化器具体参考 深度学习中的优化器原理(SGD,SGDMomentum,Adagrad,RMSProp,Adam)_哔哩哔哩_bilibili 收藏版|史上最全机器学习优化器Optimizer汇总 - 知乎 (zhihu.com) import numpy as np import matplotlib.pyplot as plt import torch # …...
学习网络编程No.9【应用层协议之HTTPS】
引言: 北京时间:2023/10/29/7:34,好久没有在周末早起了,该有的困意一点不少。伴随着学习内容的深入,知识点越来越多,并且对于爱好刨根问底的我来说,需要了解的知识就像一座大山,压得…...
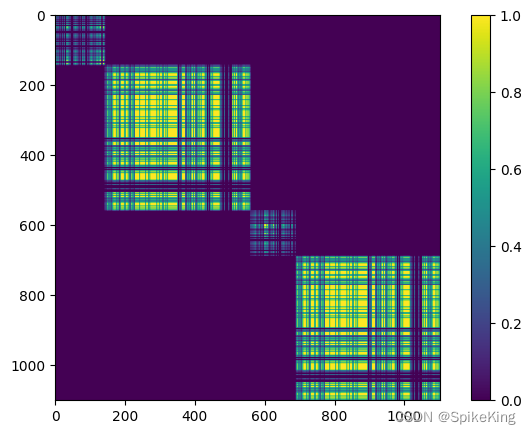
PSP - 蛋白质复合物结构预测 Template Pair 特征 Mask 可视化
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/134333419 在蛋白质复合物结构预测中,在 TemplatePairEmbedderMultimer 层中 ,构建 Template Pair 特征的源码,…...

RK3568开发笔记-amixer开机设置音量异常
目录 前言 一、amixer介绍 1. 显示音频设备信息 2. 显示音量信息...
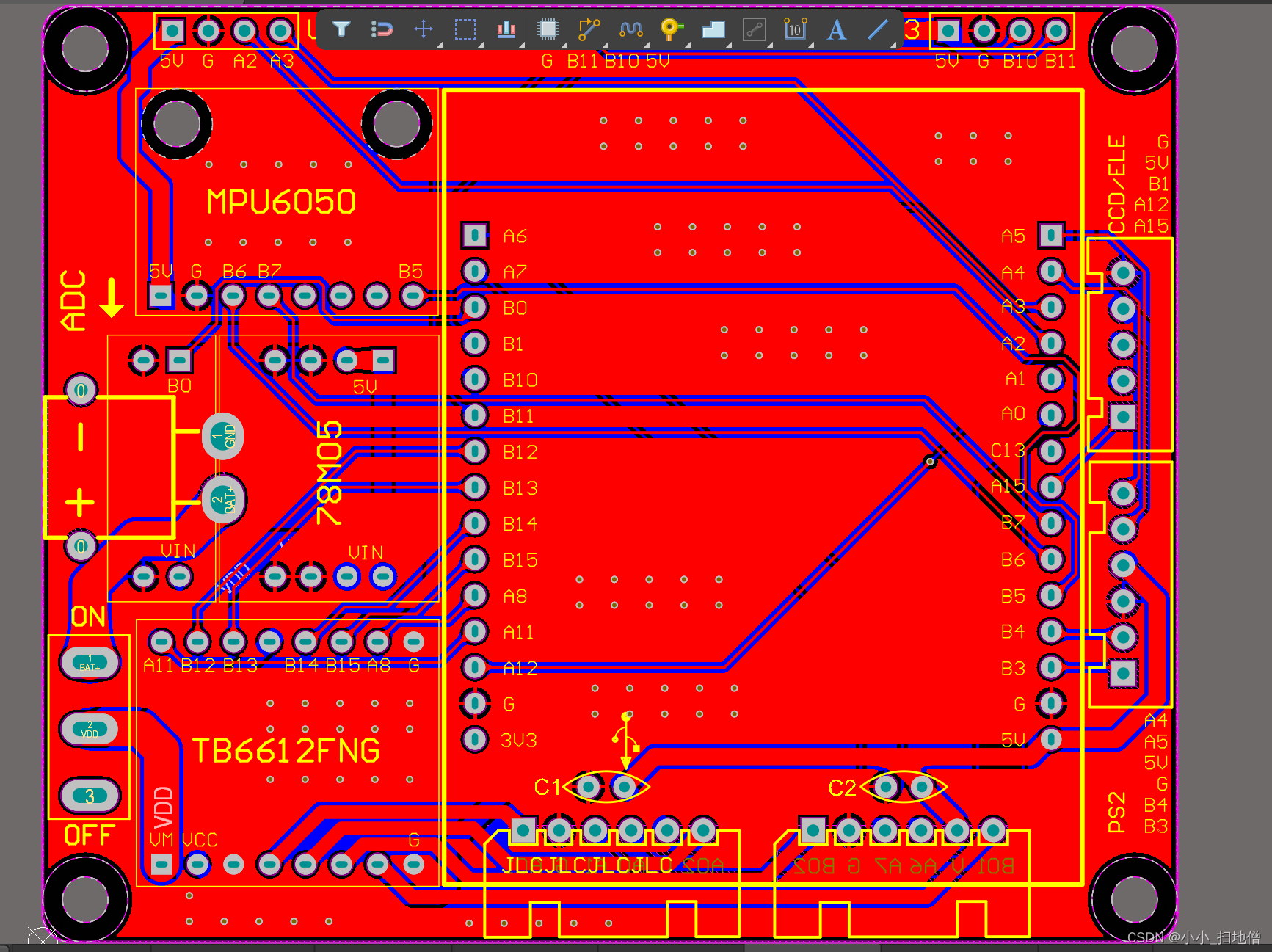
STM32两轮平衡小车原理详解(开源)
一、引言 关于STM32两轮平衡车的设计,我想在读者阅读本文之前应该已经有所了解,所以本文的重点是代码的分享和分析。至于具体的原理,我觉得读者不必阅读长篇大论的文章,只需按照本文分享的代码自己亲手制作一辆平衡车,…...
)
区间内的真素数问题(C#)
题目:区间内的真素数 找出正整数 M 和 N 之间(N 不⼩于 M)的所有真素数。真素数的定义:如果⼀个正整数P 为素数,且其反序也为素数,那么 P 就为真素数。例如,11,13 均为真素数&#…...
eclipse安装lombok插件
lombok插件下载:Download 下载完成,lombok.jar放到eclipse根目录,双击jar运行 运行界面,点击Install安装。 安装完成,重启IDE,rebuild 项目。 rebuild 项目...

故障演练 | 微服务架构下如何做好故障演练
前言 微服务架构场景中,应用系统复杂切分散。长期运行时,局部出现故障时不可避免的。如果发生故障时不能进行有效反应,系统的可用性将极大地降低。 什么是故障演练 故障演练是指模拟生产环境中可能出现的故障,测试系统或应用在…...
Python爬虫-获取汽车之家车家号
前言 本文是该专栏的第9篇,后面会持续分享python爬虫案例干货,记得关注。 地址:aHR0cHM6Ly9jaGVqaWFoYW8uYXV0b2hvbWUuY29tLmNuL0F1dGhvcnMjcHZhcmVhaWQ9MjgwODEwNA== 需求:获取汽车之家车家号数据 笔者将在正文中介绍详细的思路以及采集方法,废话不多说,跟着笔者直接往…...

No195.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

pytest与testNg自动化框架
一.pytest 1.安装pytest: pip install pytest 2.编写用例 - 收集用例 - 执行用例 - 生成报告 3.pytest如何自动识别用例 识别规则如下: 1、搜索根目录:默认从当前目录中搜集测试用例,即在哪个目录下运行pytest命令,…...

数据库安全:Hadoop 未授权访问-命令执行漏洞.
数据库安全:Hadoop 未授权访问-命令执行漏洞. Hadoop 未授权访问主要是因为 Hadoop YARN 资源管理系统配置不当,导致可以未经授权进行访问,从而被攻击者恶意利用。攻击者无需认证即可通过 RESTAPI 部署任务来执行任意指令,最终完…...

前端---认识HTML
文章目录 什么是HTML?HTML的读取、运行HTML的标签注释标签标题标签段落标签换行标签格式化标签图片标签a标签表格标签列表标签表单标签form标签input标签文本框单选框复选框普通按钮提交按钮文件选择框 select标签textarea标签特殊标签div标签span标签 什么是HTML&a…...
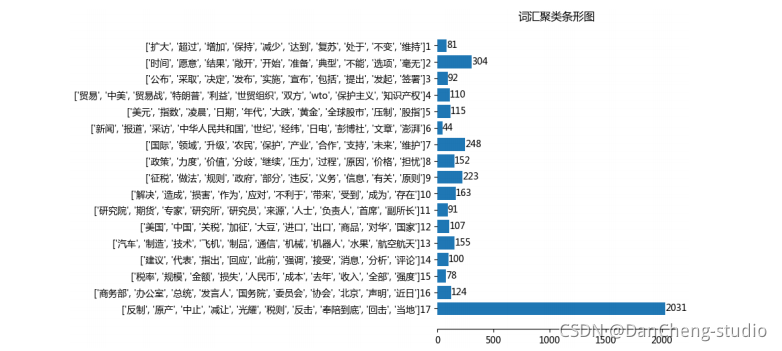
竞赛 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录 0 前言1 项目背景2 算法架构3 FP-Growth算法原理3.1 FP树3.2 算法过程3.3 算法实现3.3.1 构建FP树 3.4 从FP树中挖掘频繁项集 4 系统设计展示5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于FP-Growth的新闻挖掘算法系统的设计与实现…...

保姆级jupyter lab配置清单
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
数据结构预算法--链表(单链表,双向链表)
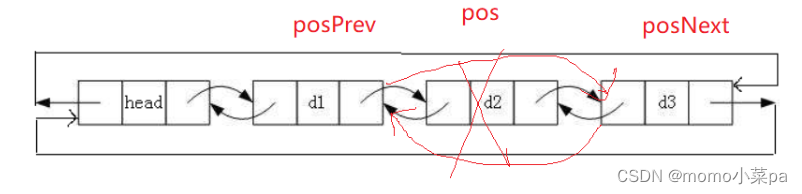
1.链表 目录 1.链表 1.1链表的概念及结构 1.2 链表的分类 2.单链表的实现(不带哨兵位) 2.1接口函数 2.2函数的实现 3.双向链表的实现(带哨兵位) 3.1接口函数 3.2函数的实现 1.1链表的概念及结构 概念:链表是一种物理存储结…...

数据结构线性表——栈
前言:哈喽小伙伴们,今天我们将一起进入数据结构线性表的第四篇章——栈的讲解,栈还是比较简单的哦,跟紧博主的思路,不要掉队哦。 目录 一.什么是栈 二.如何实现栈 三.栈的实现 栈的初始化 四.栈的操作 1.数据入栈…...

自定义 springboot 启动器 starter 与自动装配原理
Maven 依赖 classpath 类路径管理 Maven 项目中的类路径添加来源分为三类 自定义 springboot starter starter 启动器定义的规则自定义 starter 示例 自动装配 文章链接...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
