【机器学习5】无监督学习聚类
相比于监督学习, 非监督学习的输入数据没有标签信息, 需要通过算法模型来挖掘数据内在的结构和模式。 非监督学习主要包含两大类学习方法: 数据聚类和特征变量关联。
1 K均值聚类及优化及改进模型
1.1 K-means
聚类是在事先并不知道任何样本类别标签的情况下, 通过数据之间的内在关系把样本划分为若干类别, 使得同类别样本之间的相似度高, 不同类别之间的样本相似度低 。
K均值聚类(KMeans Clustering) 的基本思想是, 通过迭代方式寻找K个簇(Cluster) 的一种划分方案, 使得聚类结果对应的代价函数最小。 特别地, 代价函数可以定义为各个样本距离所属簇中心点的误差平方和 :
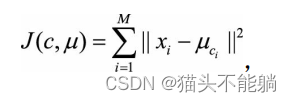 xi代表第i个样本, ci是xi所属于的簇, μci代表簇对应的中心点, M是样本总数。
xi代表第i个样本, ci是xi所属于的簇, μci代表簇对应的中心点, M是样本总数。
 K均值算法在迭代时, 假设当前 J 没有达到最小值, 那么首先固定簇中心{μk},调整每个样例xi所属的类别ci来让J函数减少; 然后固定{ci}, 调整簇中心{μk}使J减小。 这两个过程交替循环, J单调递减: 当J递减到最小值时, {μk}和{ci}也同时收敛。
K均值算法在迭代时, 假设当前 J 没有达到最小值, 那么首先固定簇中心{μk},调整每个样例xi所属的类别ci来让J函数减少; 然后固定{ci}, 调整簇中心{μk}使J减小。 这两个过程交替循环, J单调递减: 当J递减到最小值时, {μk}和{ci}也同时收敛。
1.2 调优
K均值算法的调优一般可以从以下几个角度出发:
(1) 数据归一化和离群点处理。
(2) 合理选择K值。手肘法、Gap Statistic方法。
(3) 采用核函数。核聚类方法的主要思想是通过一个非线性映射, 将输入空间中的数据点映射到高位的特征空间中, 并在新的特征空间中进行聚类。 非线性映射增加了数据点线性可分的概率, 从而在经典的聚类算法失效的情况下, 通过引入核函数可以达到更为准确的聚类结果。
1.3 改进模型
K均值算法的主要缺点如下。
(1) 需要人工预先确定初始K值, 且该值和真实的数据分布未必吻合。
(2) K均值只能收敛到局部最优, 效果受到初始值很大。
(3) 易受到噪点的影响
1.3.1 K-means++
原始K均值算法最开始随机选取数据集中K个点作为聚类中心, 而K-means++按照如下的思想选取K个聚类中心。 假设已经选取了n个初始聚类中心( 0<n<K) , 则在选取第n+1个聚类中心时, 距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。 在选取第一个聚类中心( n=1) 时同样通过随机的方法。 K-means++后续的执行和经典K均值算法相同。
2 ISODATA算法
当K值的大小不确定时, 可以使用ISODATA算法。 ISODATA的全称是迭代自组织数据分析法。当属于某个类别的样本数过少时, 把该类别去除; 当属于某个类别的样本数过多、 分散程度较大时, 把该类别分为两个子类别。 ISODATA算法在K均值算法的基础之上增加了两个操作, 一是分裂操作, 对应着增加聚类中心数; 二是合并操作, 对应着减少聚类中心数。 ISODATA算法是一个比较常见的算法, 其缺点是需要指定的参数比较多, 不仅仅需要一个参考的聚类数量K
, 还需要制定3个阈值。
下面介绍ISODATA算法的各个输入参数。
( 1) 预期的聚类中心数目K
在ISODATA运行过程中聚类中心数可以变化, K是一个用户指定的参考值, 该算法的聚类中心数目变动范围也由其决定。具体地, 最终输出的聚类中心数目常见范围是从Ko的一半, 到两倍Ko。
( 2) 每个类所要求的最少样本数目Nmin。
如果分裂后会导致某个子类别所包含样本数目小于该阈值, 就不会对该类别进行分裂操作。
( 3) 最大方差Sigma。
用于控制某个类别中样本的分散程度。 当样本的分散程度超过这个阈值时, 且分裂后满足( 1) , 进行分裂操作。
( 4) 两个聚类中心之间所允许最小距离Dmin。
如果两个类靠得非常近( 即这两个类别对应聚类中心之间的距离非常小) , 小于该阈值时, 则对这两个类进行合并操作。
3 高斯混合模型(GMM)
高斯混合模型假设每个簇的数据都是符合高斯分布(又叫正态分布) 的, 当前数据呈现的分布就是各个簇的高斯分布叠加在一起的结果。
高斯混合模型的核心思想是, 假设数据可以看作从多个高斯分布中生成出来的。 在该假设下, 每个单独的分模型都是标准高斯模型, 其均值μi和方差Σi是待估计的参数。 此外, 每个分模型都还有一个参数πi, 可以理解为权重或生成数据的概率。 高斯混合模型的公式为:
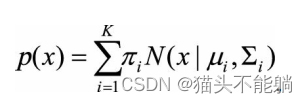 高斯混合模型是一个生成式模型。 可以这样理解数据的生成过程, 假设一个
高斯混合模型是一个生成式模型。 可以这样理解数据的生成过程, 假设一个
最简单的情况, 即只有两个一维标准高斯分布的分模型N(0,1)和N(5,1), 其权重分别为0.7和0.3。 那么, 在生成第一个数据点时, 先按照权重的比例, 随机选择一个分布, 比如选择第一个高斯分布, 接着从N(0,1)中生成一个点, 如−0.5, 便是第一个数据点。 在生成第二个数据点时, 随机选择到第二个高斯分布N(5,1), 生成了第二个点4.7。 如此循环执行, 便生成出了所有的数据点。
高斯混合模型的计算, 便成了最佳的均值μ, 方差Σ、 权重π的寻找,EM算法框架来求解该优化问题。EM算法是在最大化目标函数时, 先固定一个变量使整体函数变为凸优化函数, 求导得到最值, 然后利用最优参数更新被固定的变量, 进入下一个循环。 具体到高斯混合模型的求解, EM算法的迭代过程如下:
首先, 初始随机选择各参数的值。 然后, 重复下述两步, 直到收敛。
(1) E步骤。 根据当前的参数, 计算每个点由某个分模型生成的概率。
(2) M步骤。 使用E步骤估计出的概率, 来改进每个分模型的均值, 方差和权重。
| 算法 | 相同 | 不同 |
|---|---|---|
| K均值 | 可用于聚类;需要指定K值;使用EM算法;收敛于局部最优 | |
| 高斯混合模型 | 可用于聚类;需要指定K值;使用EM算法;收敛于局部最优 | 可以给出一个样本属于某类的概率是多少; 可以用于概率密度的估计;可以用于生成新的样本点 |
3 自组织映射神经网络(SOM)
无监督学习方法的一种,可以用作聚类、 高维可视化、 数据压缩、 特征提取等多种用途。
自组织映射神经网络本质上是一个两层的神经网络, 包含输入层和输出层(竞争层)。输入层模拟感知外界输入信息的视网膜, 输出层模拟做出响应的大脑皮层。 输出层中神经元的个数通常是聚类的个数, 代表每一个需要聚成的类。训练时采用“竞争学习”的方式, 每个输入的样例在输出层中找到一个和它最匹配
的节点, 称为激活节点, 也叫winning neuron; 紧接着用随机梯度下降法更新激活节点的参数; 同时, 和激活节点临近的点也根据它们距离激活节点的远近而适当地更新参数。
4 聚类算法的评估
4.1数据簇
为了评估不同聚类算法的性能优劣, 我们需要了解常见的数据簇的特点。
| 数据簇 | 数据分布 | 数据特点 |
|---|---|---|
| 以中心定义 | 集合中数据倾向于球形分布 | 集合中的数据到中心的距离相比到其他簇中心的距离更近 |
| 以密度定义 | 集合中数据呈现和周围数据簇明显不同的密度, 或稠密或稀疏 | 当数据簇不规则或互相盘绕, 并且有噪声和离群点时, 常常使用基于密度的簇定义 |
| 以连通定义 | 集合中的数据点和数据点之间有连接关系,整个数据簇表现为图结构 | 对不规则形状或者缠绕的数据簇有效 |
| 以概念定义 | 集合中的所有数据点具有某种共同性质 |
4.2 评估任务
4.2.1 估计聚类趋势
检测数据分布中是否存在非随机的簇结构。 如果数据是基本随机的, 那么聚类的结果也是毫无意义的。
应用霍普金斯统计量(Hopkins Statistic) 来判断数据在空间上的随机性[7]。 首先, 从所有样本中随机找n个点, 记为p1,p2,…,pn, 对其中的每一个点pi, 都在样本空间中找到一个离它最近的点并计算它们之间的距离xi, 从而得到距离向量x1,x2,…,xn; 然后, 从样本的可能取值范围内随机生成n个点, 记为q1,q2,…,qn, 对每个随机生成的点, 找到一个离它最近的样本点并计算它们之间的距离, 得到y1,y2,…,yn。 霍普金斯统计量H可以表示为:

如果样本接近随机分布, 那么分母的两个取值应该比较接近, 即H的值接近于0.5; 如果聚类趋势明显, 则随机生成的样本点距离应该远大于实际样本点的距离, 即 H值接近于1。
4.2.2 判定数据簇数
数据簇数的判定方法有很多, 例如手肘法和Gap Statistic方法。 需要说明的是, 用于评估的最佳数据簇数可能与程序输出的簇数是不同的。例如, 有些聚类算法可以自动地确定数据的簇数, 但可能与我们通过其他方法确定的最优数据簇数有所差别
4.2.3测定聚类质量
给定预设的簇数, 不同的聚类算法将输出不同的结果, 如何判定哪个聚类结果的质量更高呢? 在无监督的情况下, 我们可以通过考察簇的分离情况和簇的紧凑情况来评估聚类的效果。
| 度量指标 | 定义 | 特点 |
|---|---|---|
| 轮廓系数 | 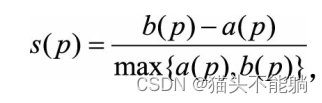 a§是点p与同一簇中的其他点p’之间的平均距离; b§是点p与另一个不同簇中的点之间的最小平均距离(如果有n个其他簇, 则只计算和点p最接近的一簇中的点与该点的平均距离) a§是点p与同一簇中的其他点p’之间的平均距离; b§是点p与另一个不同簇中的点之间的最小平均距离(如果有n个其他簇, 则只计算和点p最接近的一簇中的点与该点的平均距离) | a§反映的是p所属簇中数据的紧凑程度, b§反映的是该簇与其他临近簇的分离程度。 显然, b§越大, a§越小, 对应的聚类质量越好 |
| 均方根标准偏差 RMSSTD | 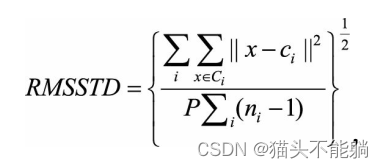 其中Ci代表第i个簇, ci是该簇的中心, x∈ Ci代表属于第i个簇的一个样本点, ni为第i个簇的样本数量, P为样本点对应的向量维数。 其中Ci代表第i个簇, ci是该簇的中心, x∈ Ci代表属于第i个簇的一个样本点, ni为第i个簇的样本数量, P为样本点对应的向量维数。 | RMSSTD可以看作是经过归一化的标准差 |
| R方(R-Square) | 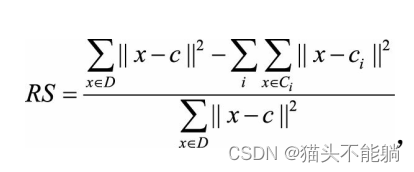 D代表整个数据集, c代表数据集D的中心点 D代表整个数据集, c代表数据集D的中心点 | RS代表了聚类之后的结果与聚类之前相比, 对应的平方误差和指标的改进幅度 |
| 改进的HubertΓ统计 | 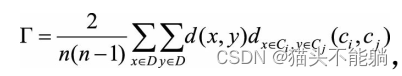 | Γ值越大说明聚类的结果与样本的原始距离越吻合, 也就是聚类质量越高 |
相关文章:
【机器学习5】无监督学习聚类
相比于监督学习, 非监督学习的输入数据没有标签信息, 需要通过算法模型来挖掘数据内在的结构和模式。 非监督学习主要包含两大类学习方法: 数据聚类和特征变量关联。 1 K均值聚类及优化及改进模型 1.1 K-means 聚类是在事先并不知道任何样…...

风景照片不够清晰锐利,四招帮你轻松解决
我们大家在拍摄风景照的时候都希望能够拍摄出清晰锐利的照片。可能会有人问:“什么是锐利?”我们可以从锐度来给大家简单解说下。锐度是反映图片平面清晰度和图像边缘对比度的一个参数。锐度较高的画面,微小的细节部分也会表现得很清晰&#…...

List中的迭代器实现【C++】
List中的迭代器实现【C】 一. list的结构二. 迭代器的区别三. 迭代器的实现i. 类的设计ii. 重载iii. !重载iiii. begin()iiiii. end()iiiii. operator* 四.测试五. const迭代器的实现i. 实现ii 优化实现 六. 整体代码 一. list的结构 其实按照习惯来说,应该要专门出…...
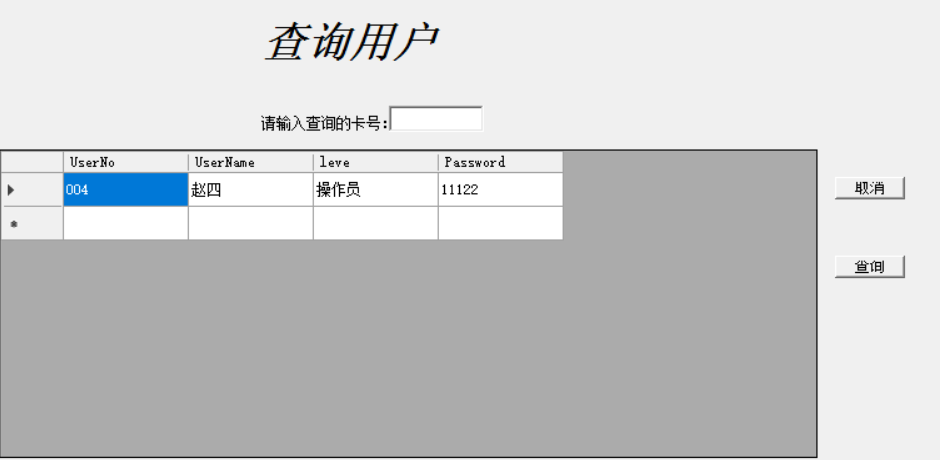
VB.NET三层之用户查询窗体
目录 前言: 过程: UI层代码展示: BLL层代码展示: DAL层代码展示: 查询用户效果图: 总结: 前言: 想要对用户进行查询,需要用到控件DataGrideView,通过代码的形式将数据库表中的数据显示在DataGrideview控件中,不用对DatGridView控件…...
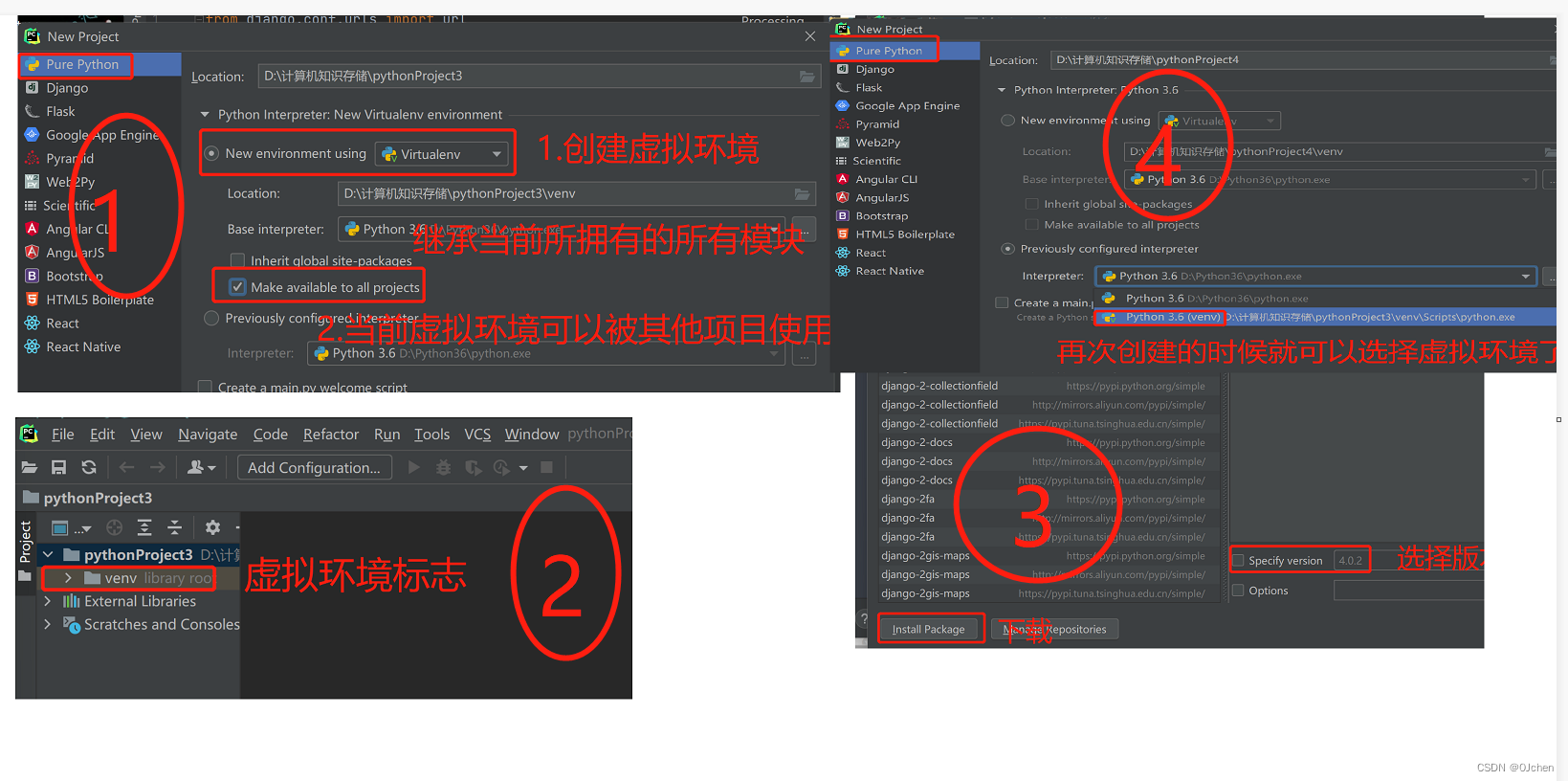
Django之路由层
文章目录 路由匹配语法路由配置注意事项转换器注册自定义转化器 无名分组和有名分组无名分组有名分组 反向解析简介普通反向解析无名分组、有名分组之反向解析 路由分发简介为什么要用路由分发?路由分发实现 伪静态的概念名称空间虚拟环境什么是虚拟环境?…...
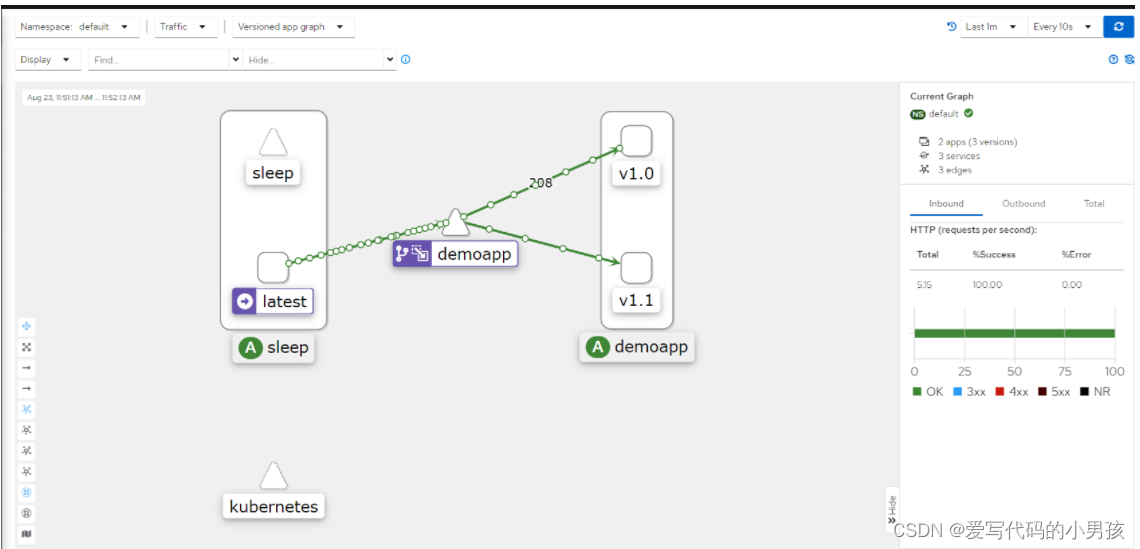
【06】VirtualService高级流量功能
5.3 weight 部署demoapp v10和v11版本 --- apiVersion: apps/v1 kind: Deployment metadata:labels:app: demoappv10version: v1.0name: demoappv10 spec:progressDeadlineSeconds: 600replicas: 3selector:matchLabels:app: demoappversion: v1.0template:metadata:labels:app…...

322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...
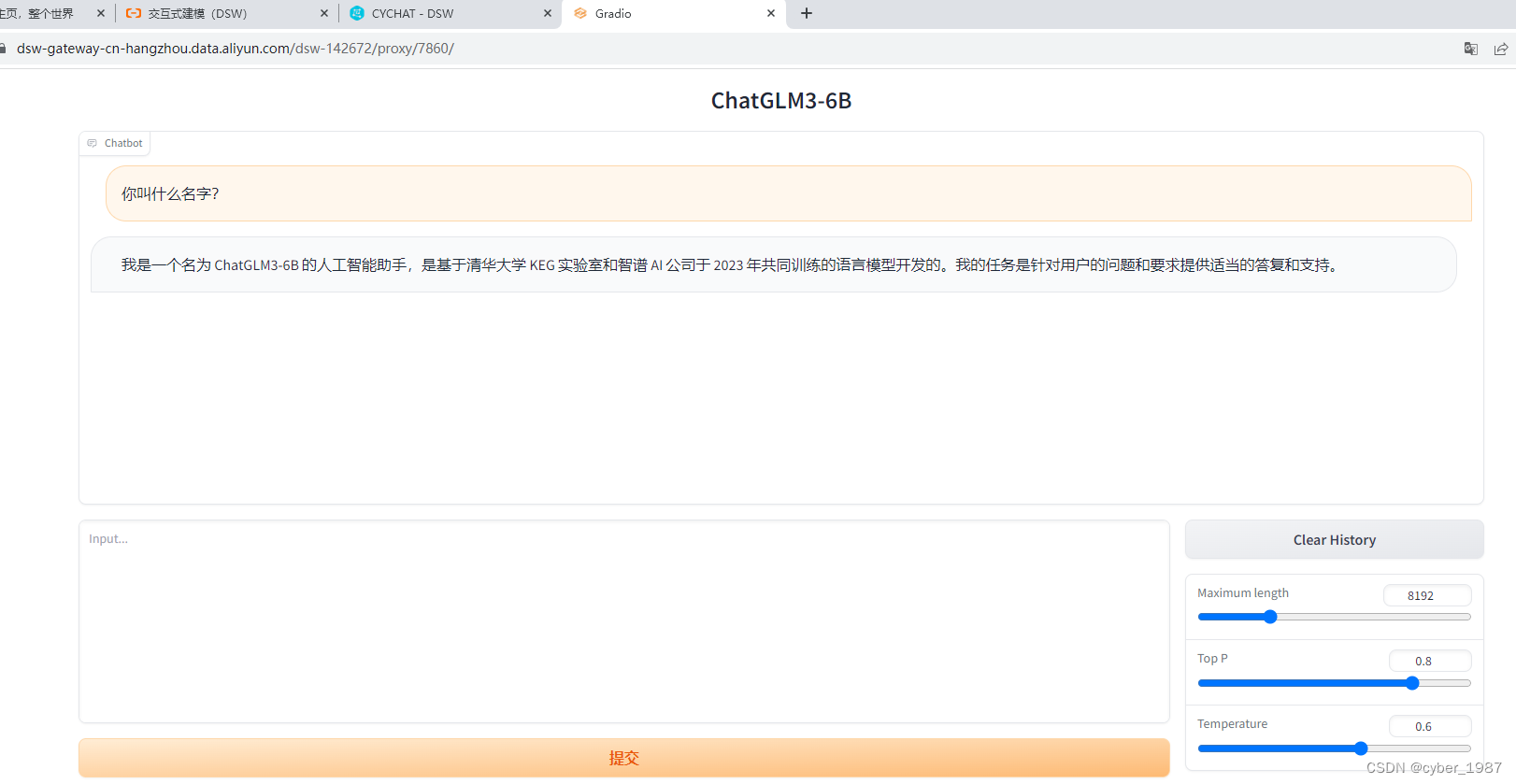
【大模型-第一篇】在阿里云上部署ChatGLM3
前言 好久没写博客了,最近大模型盛行,尤其是ChatGLM3上线,所以想部署试验一下。 本篇只是第一篇,仅仅只是部署而已,没有FINETUNE、没有Langchain更没有外挂知识库,所以从申请资源——>开通虚机——>…...

2023-11-14 mysql-主从复制-相关文档
摘要: 2023-11-14 mysql-主从复制-相关文档 官方文档: MySQL :: MySQL 8.0 Reference Manual :: 17 Replication MySQL :: MySQL 8.0 Reference Manual :: 18 Group Replication 相关参数: mysql> show variables like %repl%; +-----------------------------------------…...
ios 对话框 弹框,输入对话框 普通对话框
1 普通对话框 UIAlertController* alert [UIAlertController alertControllerWithTitle:"a" message:"alert12222fdsfs" pr…...
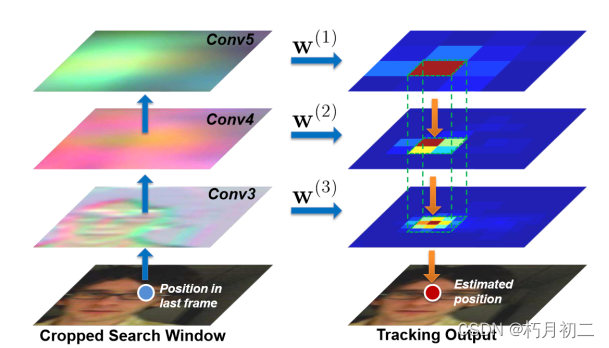
(论文阅读23/100)Hierarchical Convolutional Features for Visual Tracking
文献阅读笔记(分层卷积特征) 简介 题目 Hierarchical Convolutional Features for Visual Tracking 作者 Chao Ma, Jia-Bin Huang, Xiaokang Yang and Ming-Hsuan Yang 原文链接 arxiv.org/pdf/1707.03816.pdf 关键词 Hierarchical convolution…...

基于IGT-DSER智能网关实现GE的PAC/PLC与罗克韦尔(AB)的PLC之间通讯
工业自动化领域的IGT-DSER智能网关模块支持GE、西门子、三菱、欧姆龙、AB等各种品牌的PLC之间通讯(相关资料下载),同时也支持PLC与Modbus协议的工业机器人、智能仪表等设备通讯。网关有多个网口、串口,也可选择WIFI无线通讯。无需编程开发,只…...

创建符合 Web 可访问性标准的 HTML 布局
人们常说网络可访问性是当今万维网的“必须”。“Web 可访问性”一词定义了开发人员需要遵循的一组准则,以使残障人士和 Web 应用程序的交互更加方便。任何网站的内容、UI/UX 设计和布局都应该易于访问。在本文中,Logicify团队为 HTML/CSS 开发人员提供了…...
SQL学习(CTFhub)整数型注入,字符型注入,报错注入 -----手工注入+ sqlmap注入
目录 整数型注入 手工注入 为什么要将1设置为-1呢? sqlmap注入 sqlmap注入步骤: 字符型注入 手工注入 sqlmap注入 报错注入 手工注入 sqlmap注入 整数型注入 手工注入 先输入1 接着尝试2,3,2有回显,而3没有回显…...

数字人部署之VITS+Wav2lip数据流转处理以提高实时性
一、模型 VITS模型训练教程VITS-从零开始微调(finetune)训练并部署指南-支持本地云端 Wav2lip是2D数字人,可参考训练嘴型同步模型Wav2Lip PS:以上模型都是开源可用。 二. VITS数据处理问题 VITS模型的输出为一维的numpy类型数据ÿ…...

GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性
GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性 复杂文献 - 基础理解GPT 理解法 - 举例子、归纳、逻辑链推导本质、图示、概念放大器GPT 分析法 - 二分、矩阵、公式、要素、过程 做复杂题:在庞大的不确性中找到确定性思维追踪ÿ…...

前端简单的爱心形状
首先需要创建一个 HTML 文件,然后在其中添加 CSS 样式和 JavaScript 代码。以下是一个简单的示例: 创建一个名为 loveheart.html 的文件 <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><…...
)
acwing算法基础之数学知识--求数a的欧拉函数值phi(a)
目录 1 基础知识2 模板3 工程化 1 基础知识 数a的欧拉函数 ϕ ( a ) \phi(a) ϕ(a):表示1~n中与n互质的数的个数。其中两个数互质,是指这两个数的最大公约数为1。 根据定义,我们可以写出如下方法, int gcd(int a, int b) {retu…...
Jenkins的介绍与相关配置
Jenkins的介绍与配置 一.CI/CD介绍 1.CI/CD概念 ①CI 中文意思是持续集成 (Continuous Integration, CI) 是一种软件开发流程,核心思想是在代码库中的每个提交都通过自动化的构建和测试流程进行验证。这种方法可以帮助团队更加频繁地交付软件&#x…...

开源网安受邀参加网络空间安全合作与发展论坛,为软件开发安全建设献计献策
11月10日,在广西南宁举办的“2023网络空间安全合作与发展论坛”圆满结束。论坛在中国兵工学会的指导下,以“凝聚网络空间安全学术智慧,赋能数字经济时代四链融合”为主题,邀请了多位专家及企业代表共探讨网络安全发展与数字经济…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...
