算法:穷举,暴搜,深搜,回溯,剪枝
文章目录
- 算法基本思路
- 例题
- 全排列
- 子集
- 全排列II
- 电话号码和字母组合
- 括号生成
- 组合
- 目标和
- 组合总和
- 优美的排列
- N皇后
- 有效的数独
- 解数独
- 单词搜索
- 黄金矿工
- 不同路径III
- 总结
算法基本思路
穷举–枚举
- 画出决策树
- 设计代码
在设计代码的过程中,重点要关心到全局变量,dfs函数,和细节问题,例如有回溯,剪枝,递归出口等问题
例题
全排列

画出该全排列的决策树:
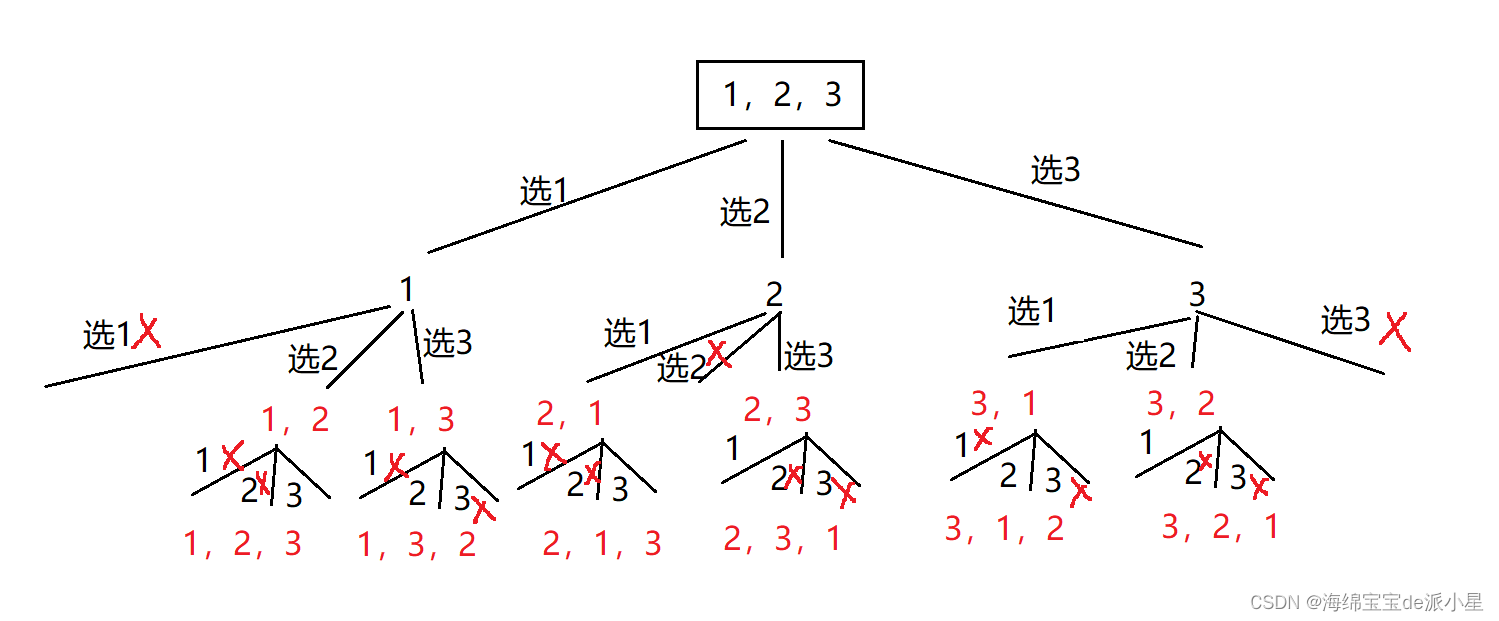
因此筛选思路也就有了,从给定的vector开始选,每选择了一个就将选的元素的下标标记为true,代表选过了,递归到下一次进行选择的时候,如果要选的元素的下标是false,代表还没有选过,就可以被选,回溯后要回复现场
class Solution
{
public:// 设计全局变量vector<vector<int>> ret; // 返回的二维数组vector<int> path; // 二维数组中的元素bool check[7]; // 判断元素是否被统计过了void dfs(vector<int>& nums){// 递归出口if(path.size() == nums.size()){ret.push_back(path);return;}for(int i=0;i<nums.size();i++){// 如果该字符没有被统计过就进行统计if(check[i] == false){path.push_back(nums[i]);check[i] = true;// 进入递归dfs(nums);// 回溯和恢复现场path.pop_back();check[i] = false;}}}vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}
};
子集

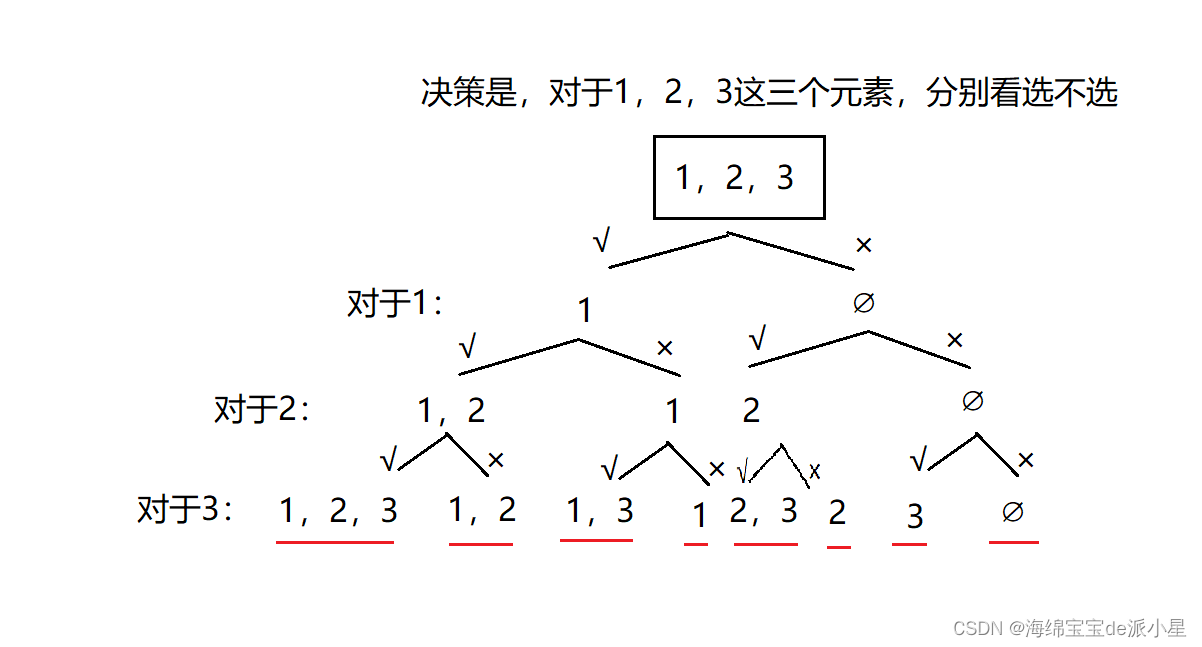
对于这个题有两种决策方案:
第一种决策方案是,对于nums数组中的每一个元素,都看它是否需要被选,可以选择要被选,也可以选择不被选
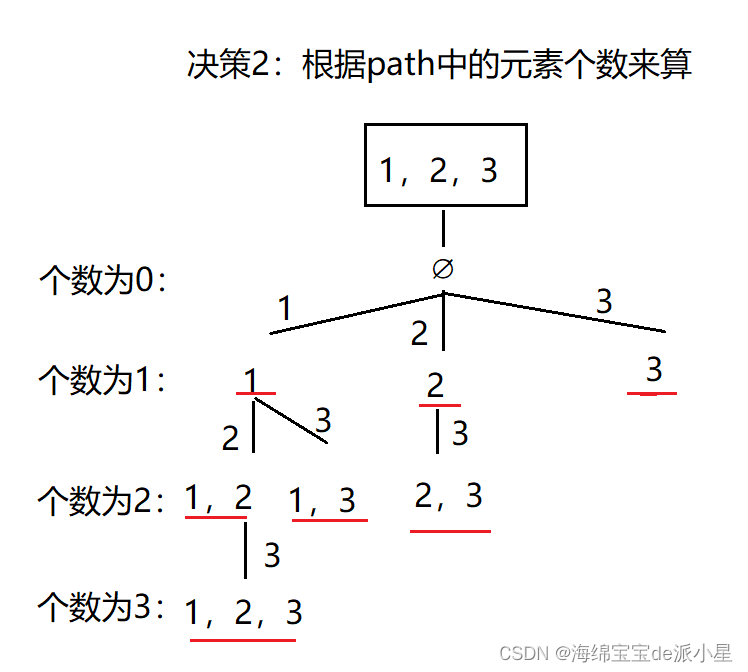
第二种决策方案是,对于path数组中的元素个数,可以为一个,也可以为两个,也可以为三个,直到和nums数组中元素的个数一样
决策1:
class Solution
{
public:vector<vector<int>> ret; // 返回值vector<int> path; // 数组中的元素void dfs(vector<int>& nums, int pos){for(int i=pos;i<nums.size();i++){// 选path.push_back(nums[i]);dfs(nums,i+1);// 不选path.pop_back();}ret.push_back(path);}vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}
};
决策2:
class Solution
{
public:vector<vector<int>> ret; // 返回值vector<int> path; // 数组中的元素void dfs(vector<int>& nums, int pos){ret.push_back(path);for(int i=pos;i<nums.size();i++){// 数组中元素的个数path.push_back(nums[i]);dfs(nums,i+1);// 回溯+恢复现场path.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}
};
全排列II

前面有做过一道全排列,这个题和前面题的不同点就是多了相同元素,因此对于剪枝的策略有不同,下面首先画出它的决策树
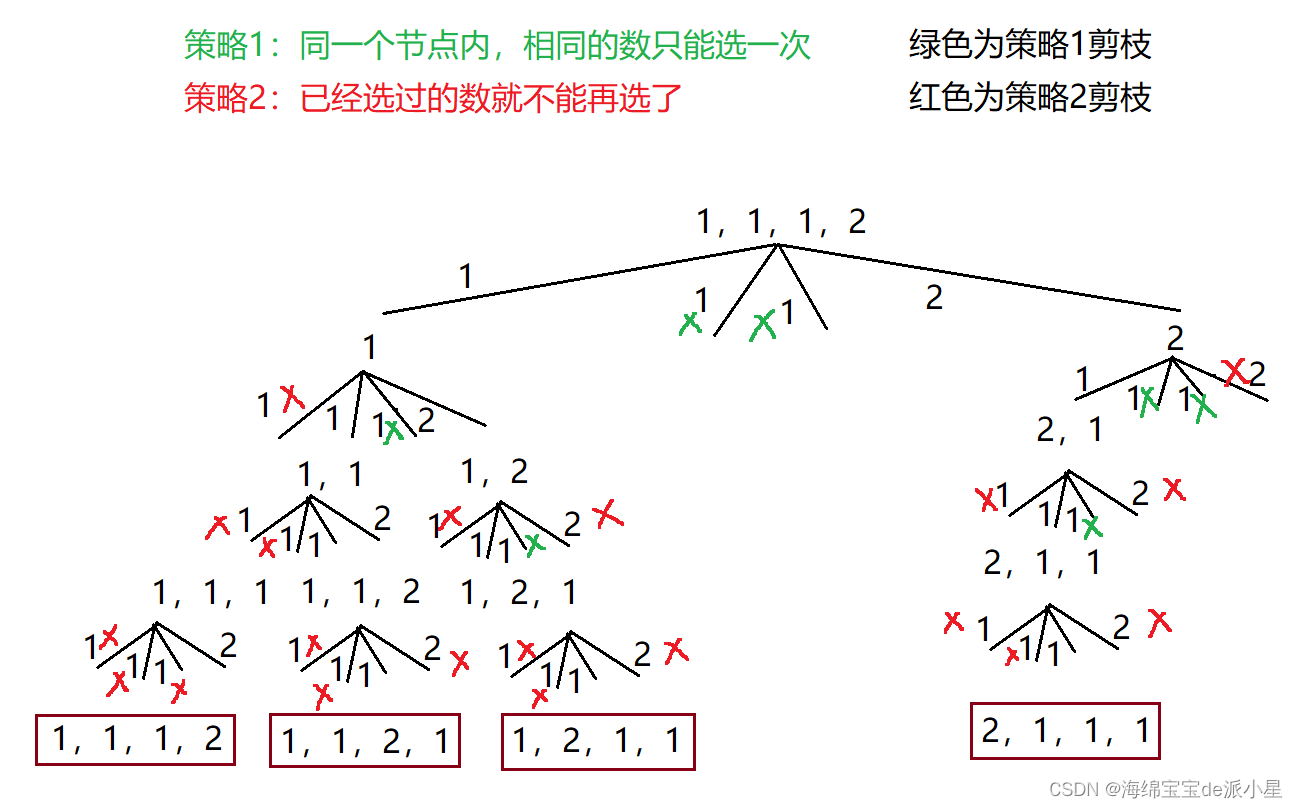
从决策树中可以看出这个题的剪枝方案
- 在同一个节点,相同的数不能被选两次 — 比较这个数有没有被选过
- 在不同的节点,已经被选过的数就不能被选了 — check数组
class Solution
{
public:// 设计全局变量vector<vector<int>> ret;vector<int> path;bool check[9];void dfs(vector<int>& nums){// 递归终止条件if(path.size() == nums.size()){ret.push_back(path);return;}for(int i = 0; i < nums.size(); i++){// 剪枝的条件:当前节点没用过并且前面没出现过if(check[i] == false && (i == 0 || nums[i] != nums[i-1] || check[i-1])){path.push_back(nums[i]);check[i] = true;dfs(nums);// 回溯check[i] = false;path.pop_back();}}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums);return ret;}
};
电话号码和字母组合
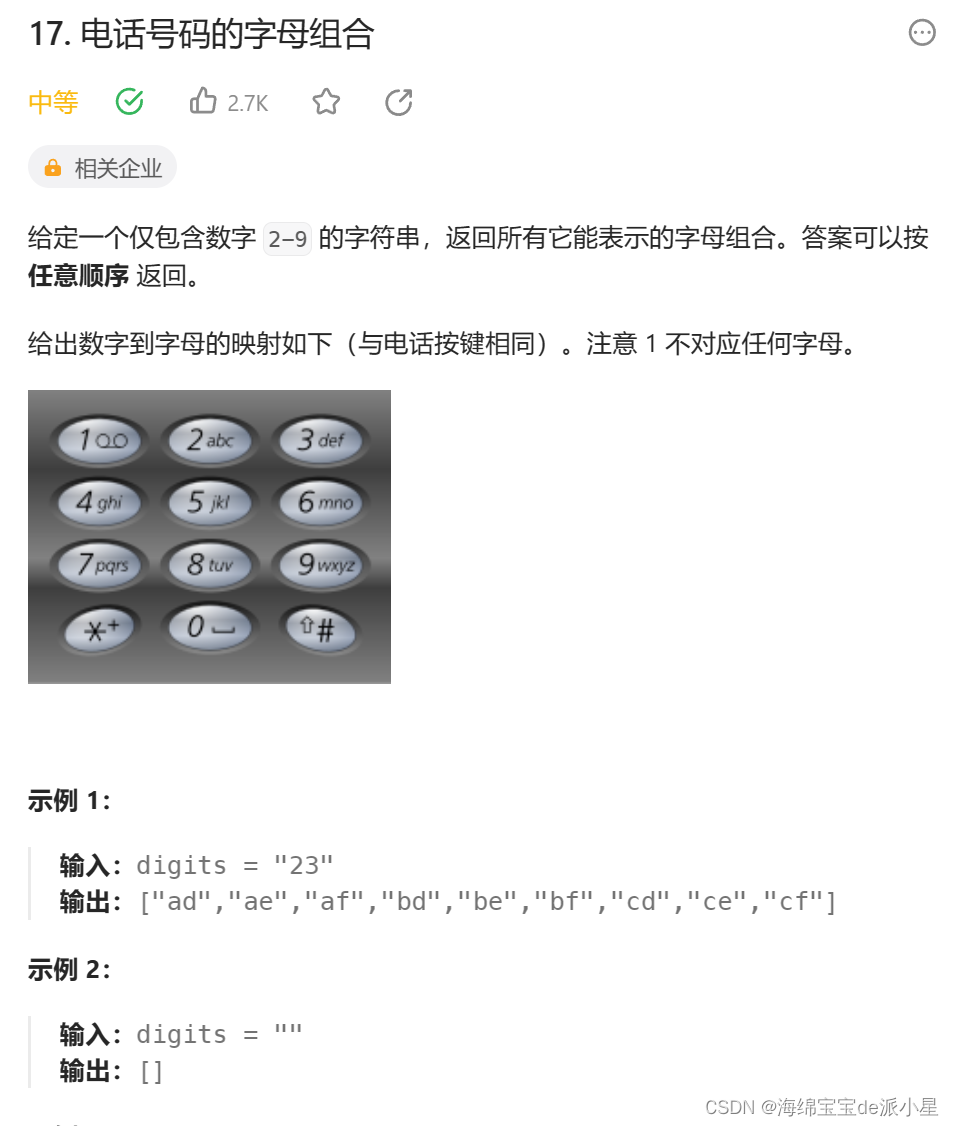
class Solution
{
public:// 全局变量string arr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};vector<string> ret;string path;// 决策:取digits中每一个数字对应的字符串中的元素,直接取即可void dfs(string& digits, int pos){// 递归终止条件if(path.size() == digits.size()){ret.push_back(path);return;}for(auto e : arr[digits[pos] - '0']){path += e;dfs(digits, pos+1);// 回溯+恢复现场path.pop_back();}}vector<string> letterCombinations(string digits) {if(digits.size() == 0)return ret;dfs(digits, 0);return ret;}
};
括号生成
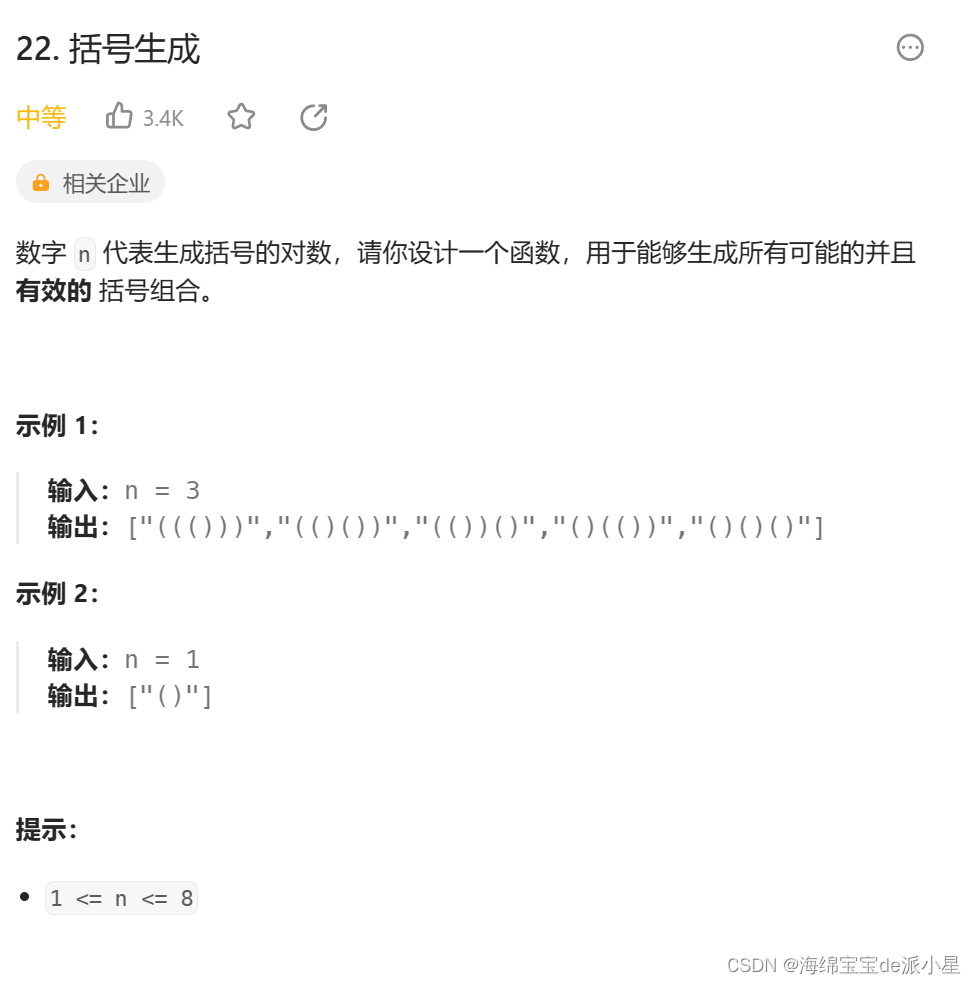
首先画出这个题的决策树,观察决策树的剪枝情况
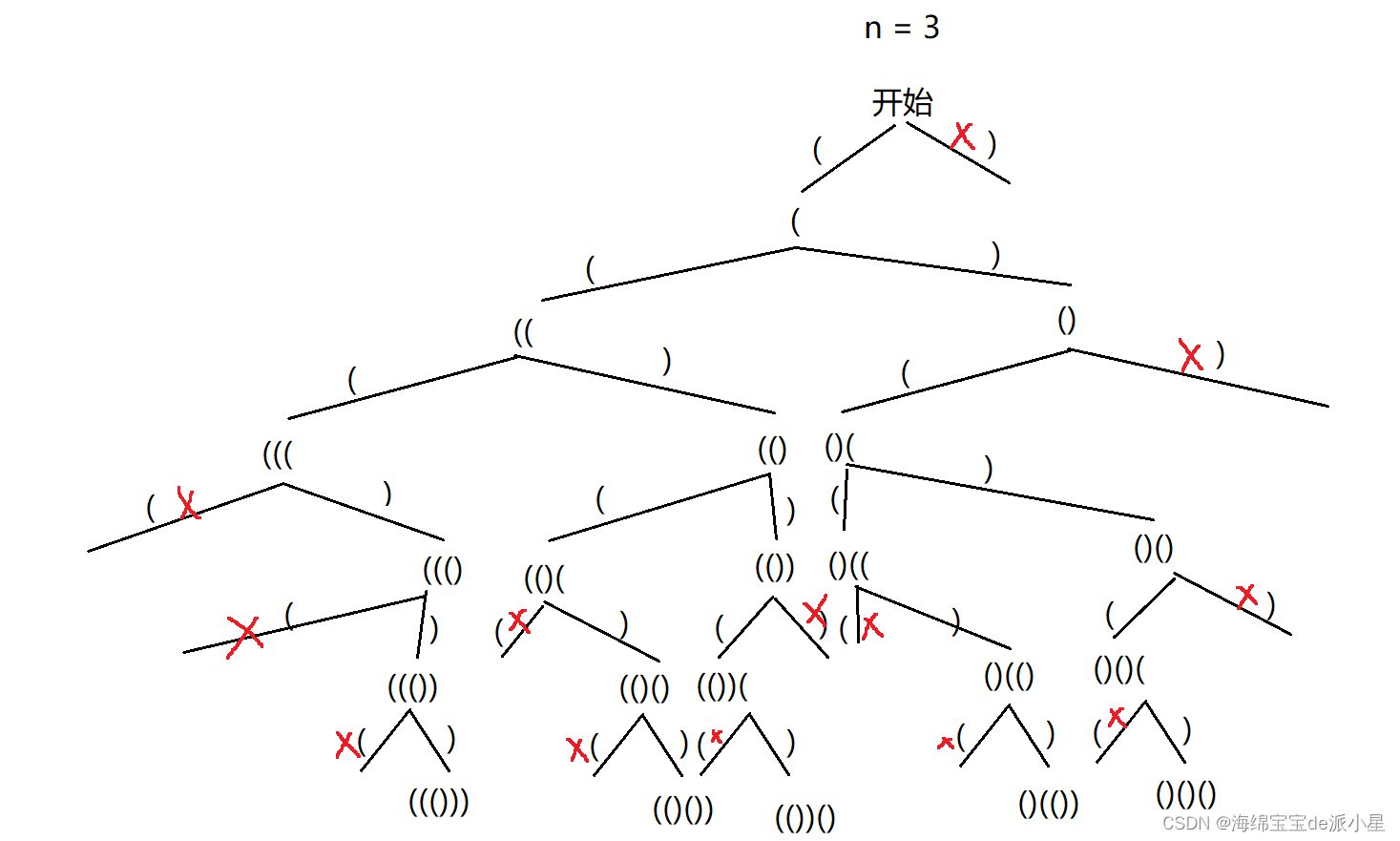
从中可以看出,这个题的剪枝条件是,右括号的数量不能大于左括号的数量,并且左括号的数量不能大于n
全局变量如何设计?答案存储在一个数组中,每一个path也要有一个字符串用以描述
递归函数头如何设计?首先必须要知道n是多少,其次要知道左括号现在有多少,右括号现在有多少
递归函数的实现细节:递归终止条件是path的长度等于n的2倍,回溯要将最后插入的部分删除掉
因此函数就很好实现了:
class Solution
{
public:vector<string> res;string path;void dfs(int n, int left, int right){// 递归终止条件if (path.size() == n * 2){res.push_back(path);return;}// 添加左括号的剪枝条件if (left < n){path += '(';left++;dfs(n, left, right);// 回溯+恢复现场path.pop_back();left--;}// 添加右括号的剪枝条件if (left > right){path += ')';right++;dfs(n, left, right);// 回溯+恢复现场path.pop_back();right--;}}vector<string> generateParenthesis(int n){dfs(n, 0, 0);return res;}
};
组合

画出决策树
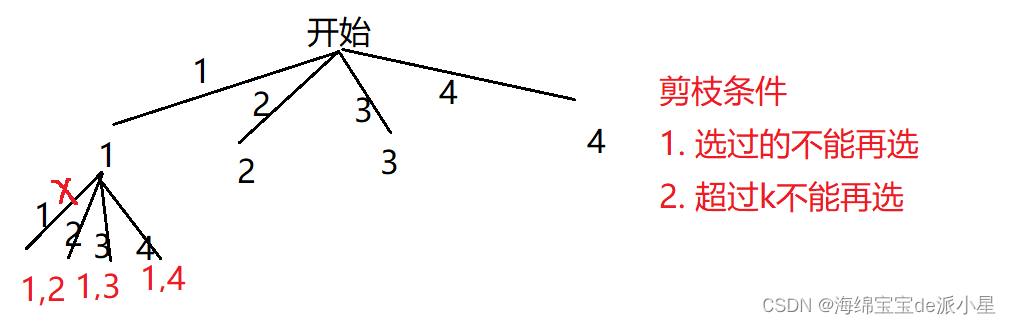
这里要注意这两个条件,其实在代码中是不需要专门体现的,首先,选过的不能再选,也就是说子集的元素都是升序排列的,那么只需要在递归的时候直接从当前位置的下一个位置开始找数即可
check数组的存在意义?
通过这个题,对于check数组有了更多的理解,check数组存在的意义是,选完一个数后,在选第二个数的过程中,需要从头再次开始选的时候,为了避免会重复选用,因此会有check数组来用以标记,但是在这个题中,选了一个数以后,选第二个数直接从这个数的下一个数开始选就可以了,因此实际上是不需要check数组来帮忙的
class Solution
{
public:// 定义全局变量vector<vector<int>> ret;vector<int> path;bool check[25];void dfs(int n, int k, int pos){// 递归终止条件if (path.size() == k){ret.push_back(path);return;}for (int i = pos; i <= n; i++){path.push_back(i);dfs(n, k, i + 1);// 回溯+恢复现场path.pop_back();}}vector<vector<int>> combine(int n, int k){dfs(n, k, 1);return ret;}
};
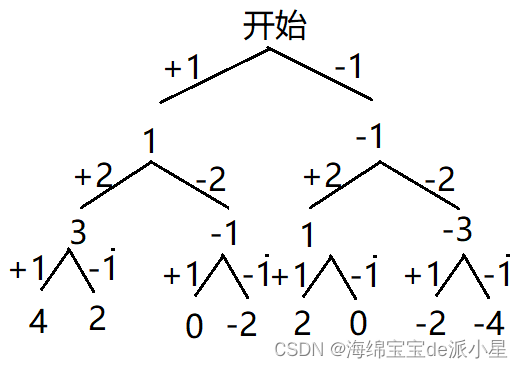
目标和

首先画出它的决策树,从中可以看出它和子集的那道题有异曲同工之处,在此基础上,对这个决策树进行实现
class Solution
{
public:// 定义全局变量int count;void dfs(vector<int>& nums, int target, int pos, int path){if (pos == nums.size()){if (path == target)count++;return;}dfs(nums, target, pos + 1, path + nums[pos]);dfs(nums, target, pos + 1, path - nums[pos]);}int findTargetSumWays(vector<int>& nums, int target){dfs(nums, target, 0, 0);return count;}
};
组合总和

决策树
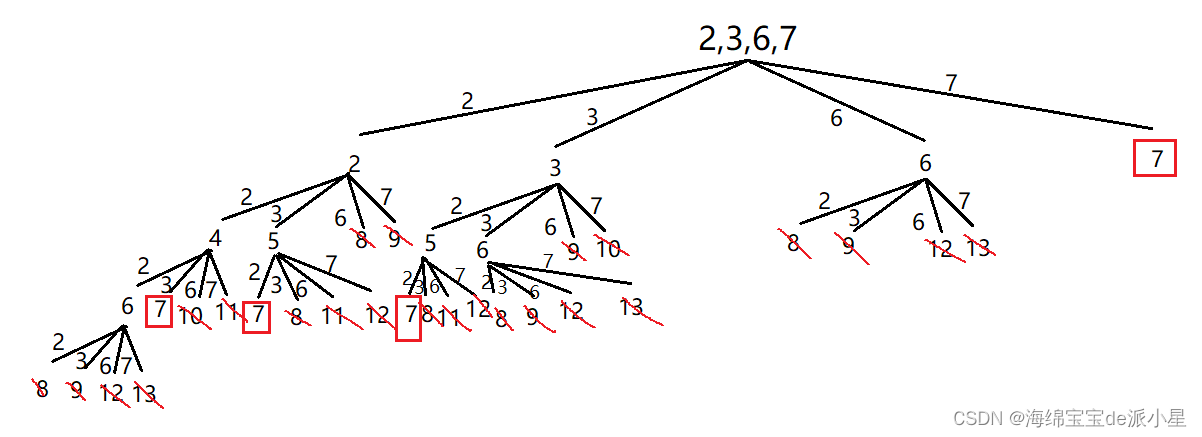
如果在不考虑去重的情况下,这样的决策树是可以的,但是这里题目要求有要去重的阶段,因此就需要考虑剪枝的问题
如何剪枝?
对于数据的选择,如果先选了2,再选3,那么在选3的时候就不应该再选2,因此剪枝的策略就是选的时候不选前面的,因为如果前面的能选,那么在前面选的时候一定选了后面的,所以只需要向前进行寻找即可,不用管后面的部分

这样的决策树才理应是正确的决策树
class Solution
{
public:// 定义全局变量vector<vector<int>> ret;vector<int> path;void dfs(vector<int>& candidates, int target, int pos, int sum){// 递归终止条件if(sum == target){ret.push_back(path);return;}if(sum > target)return;for(int i = pos; i < candidates.size(); i++){path.push_back(candidates[i]);dfs(candidates, target, i, sum + candidates[i]);// 回溯+恢复现场path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates, target, 0, 0);return ret;}
};
这是其中一种决策方案,下面提供决策的第二种思路
在数据选择方面,假设现在有2,3,5三个数字,可以对其中的每个数字选不同的次数,例如选0次,1次,2次…
优美的排列

一开始第一反应是,先把数组搞出来,再进行判断,但这样会超时,意味着有些地方需要被优化
// 超时
class Solution
{// 思路:全排列出来数据,然后判断是否优美
public:// 全局变量bool check[20];vector<int> path;int count;bool check_perm(const vector<int>& nums){for(int i = 0; i < nums.size(); i++){if(max(nums[i],i+1) % min(nums[i],i+1) != 0)return false;}return true;}void dfs(int n){// 递归终止条件if(path.size() == n){if(check_perm(path)) count++;return;}for(int i = 0; i < n; i++){if(check[i] == false){path.push_back(i + 1);check[i] = true;dfs(n);// 回溯现场path.pop_back();check[i] = false;}}}int countArrangement(int n) {dfs(n);return count;}
};
N皇后
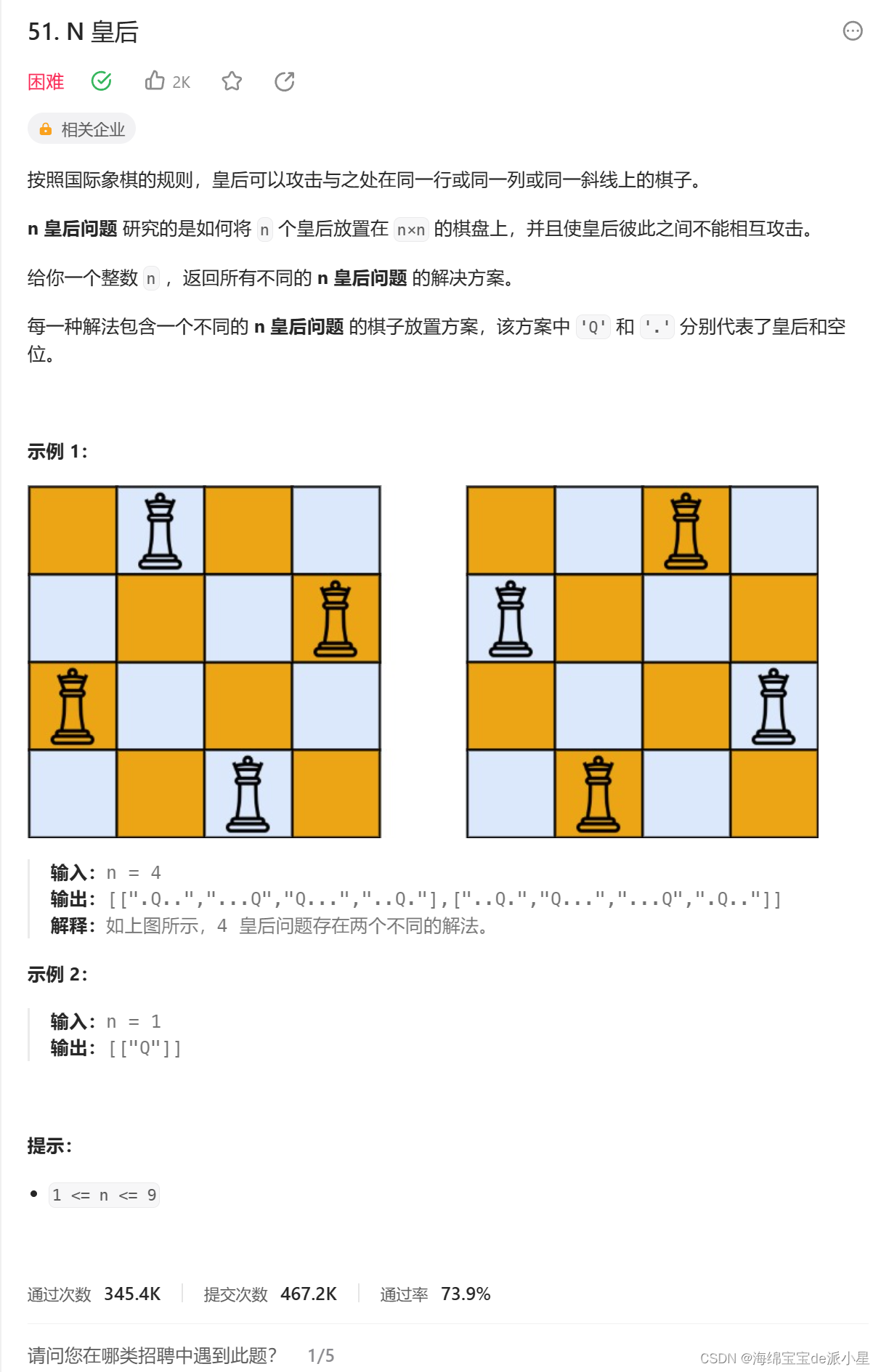
关于check判断,还可以使用类似于哈希表的解法,在下一道题中进行使用
class Solution
{
public:// 全局变量int _n;vector<vector<string>> ret;vector<string> path;// 构建皇后摆放情况string con_string(int pos, int n){string tmp;for (int i = 0; i < pos; i++)tmp += '.';tmp += 'Q';while (tmp.size() != n)tmp += '.';return tmp;}// 判断能不能在第i行的pos位置放置皇后bool check(int i, int pos){// 判断列for (int j = 0; j < i; j++){if (path[j][pos] == 'Q')return false;}// 判断主对角线for (int j = 1; i - j >= 0 && pos + j < _n; j++){if (path[i - j][pos + j] == 'Q')return false;}// 判断次对角线for (int j = 1; i - j >= 0 && pos - j >= 0; j++){if (path[i - j][pos - j] == 'Q')return false;}return true;}void dfs(int n, int pos){// 终止条件if (pos == n){ret.push_back(path);return;}for (int i = 0; i < n; i++){// 剪枝判断pos行的i位置是否可以放皇后,如果成功就放到棋盘中if (check(pos,i)){// 构建出当前皇后摆放情况string tmp = con_string(i, n);path.push_back(tmp);// 递归到下一层去判断dfs(n, pos + 1);// 回溯 恢复现场path.pop_back();}}}vector<vector<string>> solveNQueens(int n){_n = n;dfs(n, 0);return ret;}
};
有效的数独

此题就是利用了类似哈希表的方法
class Solution
{
public:// 利用哈希表的原理来解题// 全局变量:col/row[i][j]表示第i行/列中j元素是否出现过,grid是把每个九宫格当成一个元素bool col[9][10];bool row[9][10];bool grid[3][3][10];bool isValidSudoku(vector<vector<char>>& board) {for(int i = 0; i < board.size(); i++){for(int j = 0; j < board[i].size(); j++){if(board[i][j] == '.') continue;if(col[i][board[i][j] - '0'] == false){col[i][board[i][j] - '0'] = true;}else{return false;}if(row[j][board[i][j] - '0'] == false){row[j][board[i][j] - '0'] = true;}else{return false;}if(grid[i / 3][j / 3][board[i][j] - '0'] == false){grid[i / 3][j / 3][board[i][j] - '0'] = true;}else{return false;}}}return true;}
};
解数独

解决本题需要依赖前面的思想
class Solution
{
public:// 全局变量bool col[9][10];bool row[9][10];bool grid[3][3][10];void solveSudoku(vector<vector<char>>& board) {for(int i = 0; i < 9; i++){for(int j = 0; j < 9; j++){if(board[i][j] != '.'){col[j][board[i][j] - '0'] = true;row[i][board[i][j] - '0'] = true;grid[i / 3][j / 3][board[i][j] - '0'] = true;}}}dfs(board);}bool dfs(vector<vector<char>>& board){// 构造行和列for(int i = 0; i < 9; i++){for(int j = 0; j < 9; j++){if(board[i][j] == '.'){for(int num = 1; num <= 9; num++){// 剪枝if(!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num]){board[i][j] = num + '0';row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;if(dfs(board) == true)return true;// 回溯+恢复现场board[i][j] = '.';row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = false;}}return false;}}}return true;}
};
单词搜索
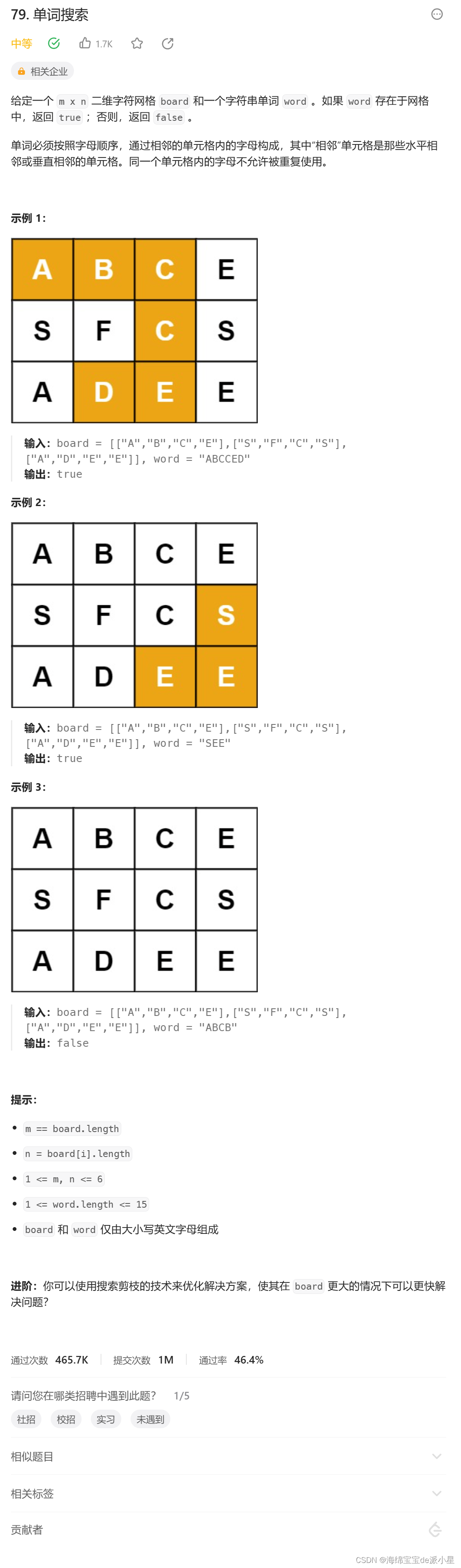
本题是使用的是矩阵中的搜索,有些类似于迷宫问题
其中需要注意的是在判断上下左右是否有内容的时候,要使用的是一个向量来标记,这样就可以避免写四层循环带来的代码冗余,在解决矩阵搜索的内容中这样的方法很方便使用
class Solution
{
public:// 全局变量 m为行数,n为列数int m;int n;string target;bool status;string path;bool check[7][7];int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};// pos代表的是现在正在寻找的元素对应的下标void dfs(vector<vector<char>>& board, int p, int q, int pos){if (pos == target.size()){status = true;return;}// 去这个格子上下左右进行寻找for(int i = 0; i < 4; i++){int row = p + dx[i];int col = q + dy[i];if (row < m && row >= 0 && col < n && col >= 0 && board[row][col] == target[pos] && check[row][col] == false){// 说明找到了,到下一层去找找check[row][col] = true;path.push_back(board[row][col]);dfs(board, row, col, pos + 1);// 回溯 恢复现场check[row][col] = false;path.pop_back();}}}bool exist(vector<vector<char>>& board, string word){m = board.size();n = board[0].size();target = word;// 此时说明已经找到了target[0],于是可以继续寻找path.push_back(target[0]);for (int i = 0; i < board.size() && status == false; i++){for(int j = 0; j< board[i].size(); j++){if(board[i][j] == target[0]){check[i][j] = true;dfs(board, i, j, 1);check[i][j] = false;}}}return status == true;}
};
黄金矿工

策略:找到有黄金的格子,从这个格子开始进行深度优先遍历,每次遍历到找不见路就停止,中间记录黄金数
class Solution
{// 策略:找到有黄金的格子,从这个格子开始进行深度优先遍历,每次遍历到找不见路就停止,中间记录黄金数
public:// 全局变量int res; // 获得黄金最多的数量bool check[16][16]; // 判断这个格子有没有走过// 定义偏移量int dx[4] = { 0, 0, 1, -1 };int dy[4] = { 1, -1, 0, 0 };// 从第i行第j列开始开采,开采量是pathvoid dfs(vector<vector<int>>& grid, int i, int j, int path){res = max(res, path);for (int k = 0; k < 4; k++){int x = dx[k] + i, y = dy[k] + j;// 剪枝 如果这个格子有矿并且没有被走过if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] != 0 && check[x][y] == false){check[x][y] = true;dfs(grid, x, y, path + grid[x][y]);// 回溯和恢复现场check[x][y] = false;}}}int getMaximumGold(vector<vector<int>>& grid){for (int i = 0; i < grid.size(); i++){for (int j = 0; j < grid[i].size(); j++){if (grid[i][j] != 0){// 标记该处已经被开采了check[i][j] = true;// 从i j开始开采,开采量是grid[i][j]dfs(grid, i, j, grid[i][j]);// 回溯和恢复现场check[i][j] = false;}}}return res;}
};
不同路径III

class Solution
{
public:bool check[21][21];int ret;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int step;void dfs(vector<vector<int>>& grid, int i, int j, int count){if(grid[i][j] == 2){if(count == step)ret++;return;}for(int k = 0; k < 4; k++){int x = i + dx[k], y = j + dy[k];if(x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] != -1 && check[x][y] == false){check[x][y] = true;dfs(grid, x, y, count + 1);check[x][y] = false;}}}int uniquePathsIII(vector<vector<int>>& grid) {int x, y;for(int i = 0; i < grid.size(); i++){for(int j = 0; j < grid[0].size(); j++){if(grid[i][j] == 1){x = i;y = j;}else if(grid[i][j] == 0){step++;}}}step += 2;check[x][y] = true;dfs(grid, x, y, 1);return ret;}
};
总结
其实从这些题中不难看出,画出决策树的过程并不困难,困难的是对于代码变现能力,因此在掌握代码变现的能力后再解决问题就很轻松了
相关文章:

算法:穷举,暴搜,深搜,回溯,剪枝
文章目录 算法基本思路例题全排列子集全排列II电话号码和字母组合括号生成组合目标和组合总和优美的排列N皇后有效的数独解数独单词搜索黄金矿工不同路径III 总结 算法基本思路 穷举–枚举 画出决策树设计代码 在设计代码的过程中,重点要关心到全局变量ÿ…...
蓝桥杯 选择排序
选择排序的思想 选择排序的思想和冒泡排序类似,是每次找出最大的然后直接放到右边对应位置,然后将最 右边这个确定下来(而不是一个一个地交换过去)。 再来确定第二大的,再确定第三大的… 对于数组a[],具体…...
20. 深度学习 - 多层神经网络
Hi,你好。我是茶桁。 之前两节课的内容,我们讲了一下相关性、显著特征、机器学习是什么,KNN模型以及随机迭代的方式取获取K和B,然后定义了一个损失函数(loss函数),然后我们进行梯度下降。 可以…...

短剧小程序:让故事更贴近生活
在当今快节奏的生活中,人们渴望找到一种能够放松身心、缓解压力的方式。短剧小程序正是这样一种贴心的产品,它以简洁、便捷、个性化的特点,让故事更加贴近生活,成为人们茶余饭后的最佳消遣。 一、短剧小程序的魅力 随时随地&…...

前端下载文件重命名
//引入使用 downloadFileRename(url,name.ext) //下载文件并重命名 export function downloadFileRename(url, filename) { function getBlob(url) { return new Promise((resolve) > { const xhr new XMLHttpRequest() xhr.open(GET, url, true) …...
【23真题】厉害,这套竟有150分满分!
今天分享的是23年中国海洋大学946的信号与系统试题及解析。 本套试卷难度分析:22年中国海洋大学946考研真题,我也发布过,若有需要,戳这里自取!平均分为109-120分,最高分为150分满分!本套试题内容难度中等&…...
44. Adb调试QT开发的Android程序实用小技巧汇总
1. 说明 使用QT开发Android应用时,如果程序本身出现了问题,很难进行调试。不像在linux或者windows系统中,可以利用QtCreator软件本身进行一些调试,安卓应用一旦在系统中安装后,如果运行中途出现什么BUG,定位问题所在很麻烦。不过,好在有adb这种调试工具可以代替QtCreat…...
nacos集群配置(超完整)
win配置与linux一样,换端口或者换ip,文章采用的 linux不同IP,同一端口 节点ipportnacos1192.168.253.168848nacos2192.168.253.178848nacos3192.168.253.188848 单IP多个端口 1.复制两个,重命名 2.修改 conf目录下的 application…...
 无线信号探测(目前仅kismet))
无线WiFi安全渗透与攻防(三) 无线信号探测(目前仅kismet)
这里写目录标题 一. kismet1.软件介绍2.软件使用1.查看kali是否链接了无线网卡2.启动kismet3.查看此时的网卡配置4.访问kismet管理界面5.打开图形窗口,第一次使用时,将会进入用户信息设置界面,如下图:6.填写相关用户信息,第一行用户名,第二行密码,第三行重复密码,设置完…...
Flutter的Widget, Element, RenderObject的关系
在Flutter中,Widget,Element和RenderObject是三个核心的概念,它们共同构成了Flutter的渲染流程和组件树的基础。下面简要介绍它们之间的关系: 1.Widget Widget是Flutter应用中的基础构建块,是一个配置的描述…...

测试员练就什么本领可以让自己狂揽10个offer
最近,以前的一个小徒弟又双叒叕跳槽了,也记不清他这是第几次跳槽了,不过从他开始做软件测试开始到现在已经有2-3年的工作经验了,从一开始的工资8K到现在的工资17K,不仅经验上积累的很多,财富上也实现了翻倍…...

vue中实现图片懒加载的几种方法
Vue-lazyload 是一个基于 Vue.js 的图片懒加载库,它的实现原理是基于 Intersection Observer API。Intersection Observer API 是一种异步观察目标元素与其祖先元素或顶级文档视窗交叉状态的方式。 Vue-lazyload 的实现原理如下: 在需要懒加载的图片元素…...
Axure9基本操作
产品经理零基础入门(四)Axure 原型图教程,2小时学会_哔哩哔哩_bilibili Axure 9 从入门到精通全集,自学必备_哔哩哔哩_bilibili 1. ① 页面对应页面个数,概要对应每个页面的具体内容 ② 文件类型 ③ 备用间隔改为5分…...

Docker - 网络
Docker - 网络 理解Docker0 # 我们发现这个容器带来网卡,都是一对对的 # evth-pair 就是一对的虚拟设备接口,他们都是成对出现的,一段连着协议,一段彼此相连 # 正因为有了这个特性,evth-pair 充当一个桥梁࿰…...

vue、react中虚拟的dom
React中虚拟DOM的例子: 下面是一个使用React创建的简单的计数器组件: import React, { Component } from react;class Counter extends Component {constructor(props) {super(props);this.state {count: 0};}handleClick () > {this.setState({c…...
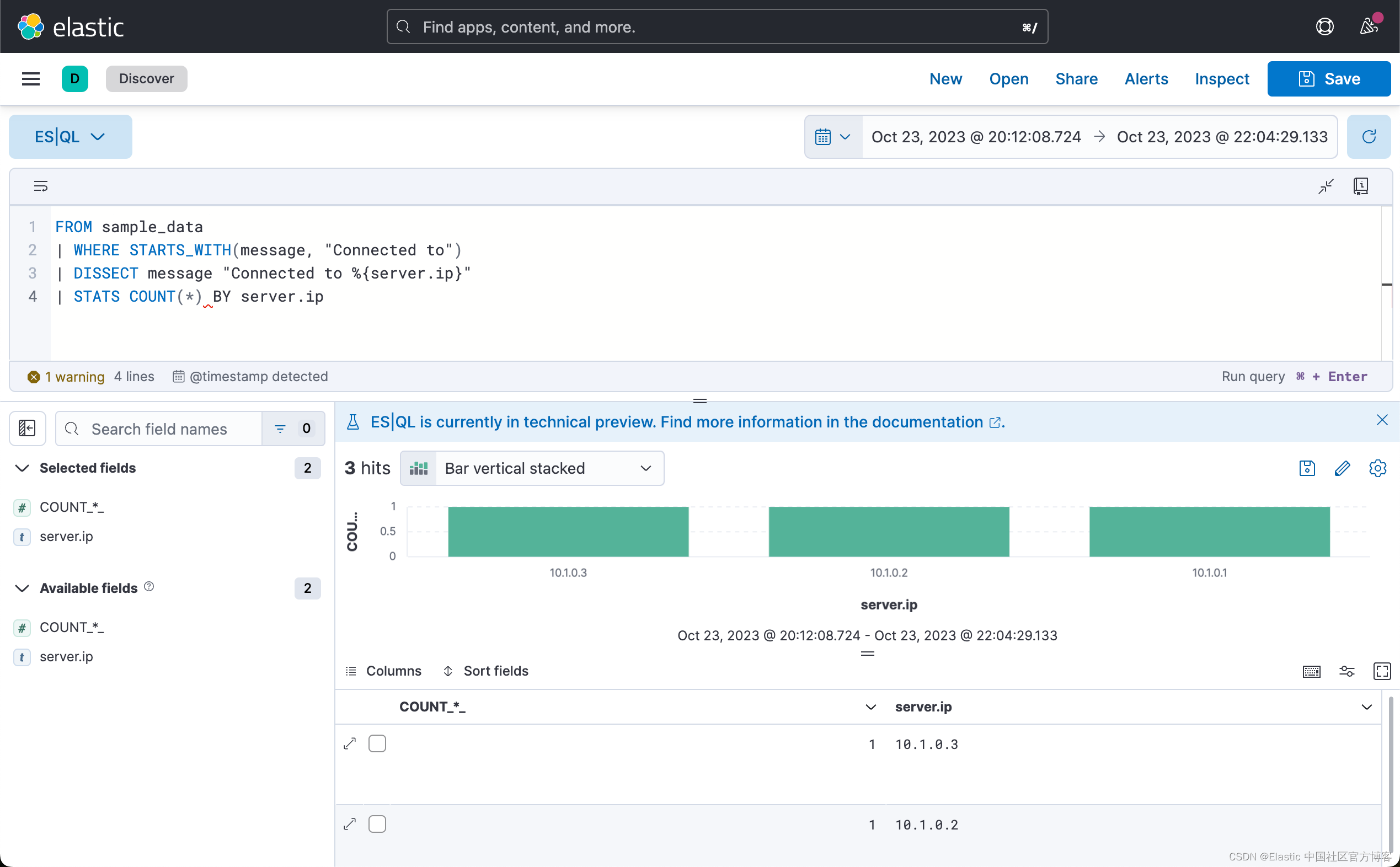
Elasticsearch:ES|QL 快速入门
警告:此功能处于技术预览阶段,可能会在未来版本中更改或删除。 Elastic 将努力解决任何问题,但技术预览版中的功能不受官方 GA 功能的支持 SLA 的约束。目前的最新发行版为 Elastic Stack 8.11。 Elasticsearch 查询语言 (ES|QL) 提供了一种强…...

7-1 进步排行榜
7-1 进步排行榜 分数 10 作者 黄龙军 单位 绍兴文理学院 假设每个学生信息包括“用户名”、“进步总数”和“解题总数”。解题进步排行榜中,按“进步总数”及“解题总数”生成排行榜。要求先输入n个学生的信息;然后按“进步总数”降序排列;若…...
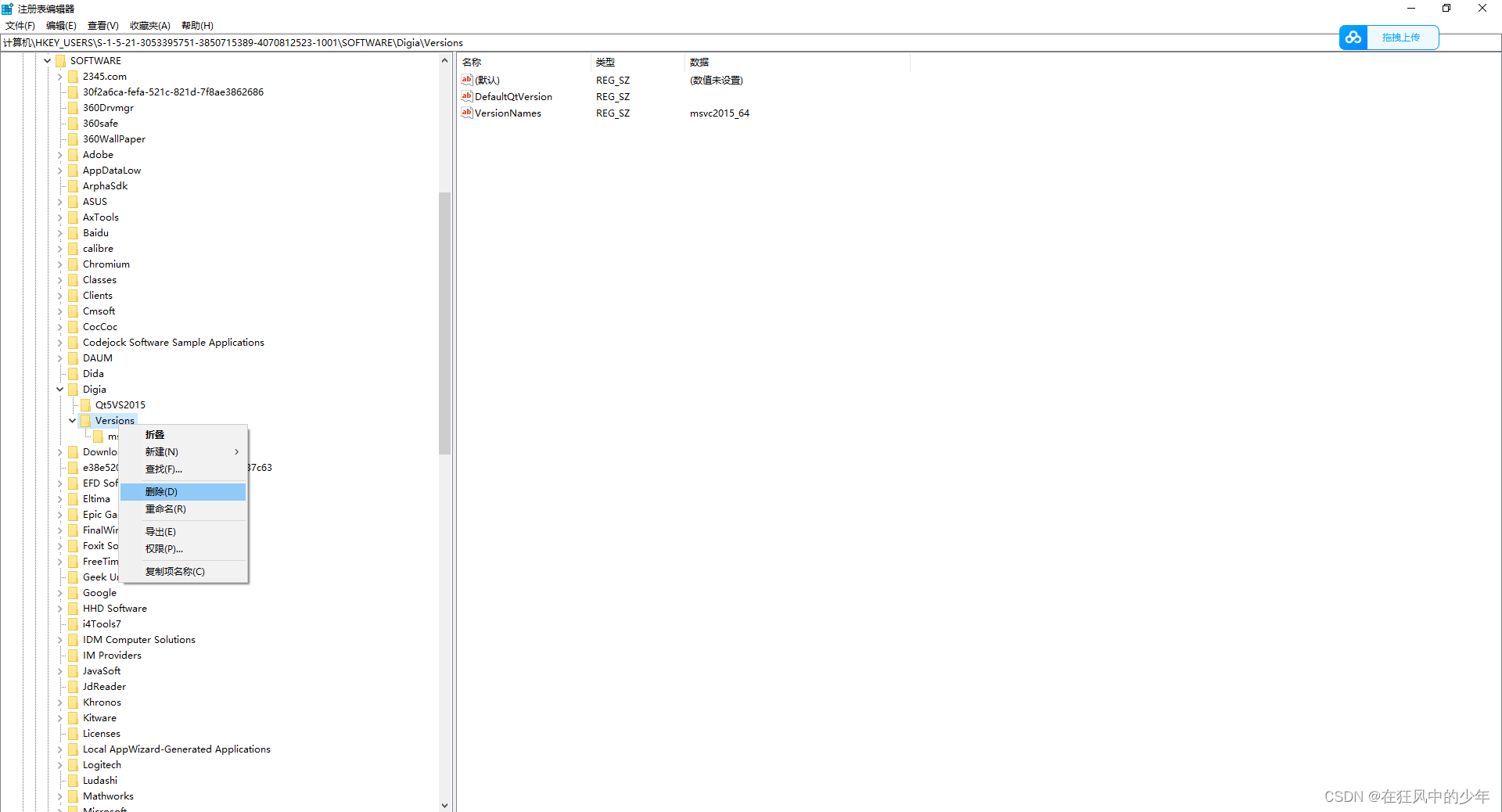
解决删除QT后Qt VS Tools中Qt Options中未删除的错误
在Qt VS Tools的Qt Options已经配置好Qt Versions后如果删除QT程序之后会出现Default Qt/Win version任然存在,这是如果再添加一个话就不能出现重名了,如果新建一个其他名字的话其实在vs中还是不能正常运行qt,会出现点击ui文件vs会无故重启或…...
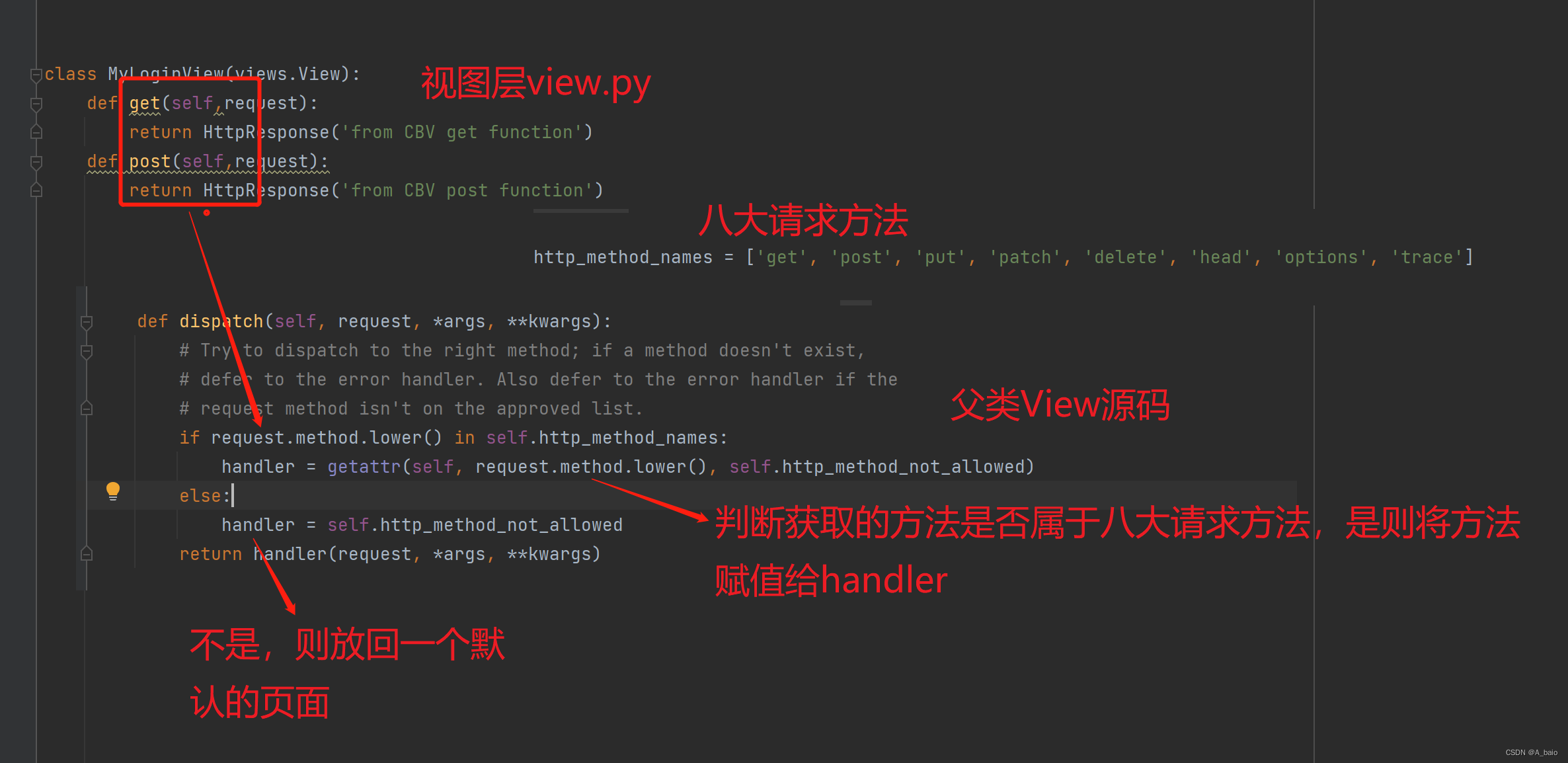
Django(五、视图层)
文章目录 一、视图层1.视图函数返回值的问题2.三板斧的使用结论:在视图文件中写视图函数的时候不能没有返回值,默认返回的是None,但是页面上会报错,用来处理请求的视图函数都必须返回httpResponse对象。 二、JsonReponse序列化类的…...
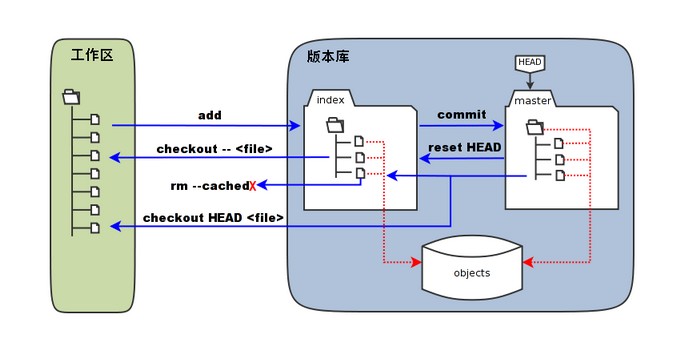
Git 工作流程、工作区、暂存区和版本库
目录 Git 工作流程 Git 工作区、暂存区和版本库 基本概念 Git 工作流程 本章节我们将为大家介绍 Git 的工作流程。 一般工作流程如下: 克隆 Git 资源作为工作目录。在克隆的资源上添加或修改文件。 如果其他人修改了,你可以更新资源。在提交前查看…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
