C/CPP基础练习题多维数组,矩阵转置,杨辉三角详解
多维数组
1. 矩阵转置
输入一个数字构成的矩形, 将矩形的值进行转置后打印
输入:
第一行 正整数n(1<n<10), 表示矩阵的边长
随后输入一个矩阵
输出:
转置后的矩阵
样例输入:
3
1 2 3
4 5 6
7 8 9
样例输出:
1 4 7
2 5 8
3 6 9
2. 颈椎病治疗
最近云海学长一直对着电脑改bug, 颈椎不舒服, 希望各位小伙伴帮云海学长治治
提供一张图片, 将图片旋转后再发给云海学长, 这样学长看图的时候就需要歪着脖子, 时间久了, 颈椎病就治好了
输入一个数字构成的矩形, 将矩形的值进行90度旋转后打印
输入:
第一行 正整数n(1<n<10), 表示矩阵的边长
随后输入一个矩阵
输出:
90度旋转后的矩阵
样例输入:
3
1 2 3
4 5 6
7 8 9
样例输出:
7 4 1
8 5 2
9 6 3
3. 杨辉三角
输入n(1<n<10), 打印高度为n的杨辉三角
样例输入: 5
样例输出:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
*4. 包围圈
东东哥在一场军事演练中, 需要对一片正方形森林进行排查,
为了防止被包围, 东东哥需要先排查外围才能进一步深入
输入: 正整数n(1<n<10), 表示森林的边长
输出: 东东哥排查森林的顺序
样例输入:
4
样例输出:
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7解答
1.矩阵转置
#include<iostream>
using namespace std;
const int N = 10;
//按数字顺序生成二维数组
void FuZhi(int n,int a[][10])
{int k = 0; for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){k++;a[i][j] = k;}}
}
//转置,行和列互换
void ZhuanZ(int n,int a[][N])
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (i > j){int t = a[i][j];a[i][j] = a[j][i];a[j][i] = t;}}}
}
//打印
void Print(int n,int a[][10])
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cout<<a[i][j];}cout << endl;}
}
int main()
{int n; cin >> n;if (n > 1 && n <= N) {int a[N][N];FuZhi(n, a);Print(n, a);cout << "转置后:" << endl;ZhuanZ(n, a);Print(n, a);}
system("pause"); return 0;
}
// 矩阵转置
void Demo61() {//--变量声明--// 矩阵边长, 矩阵本身, 转置后数组int size, arr[10][10], result[10][10];//--接收输入--scanf_s("%d", &size);for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {scanf_s("%d", &arr[i][j]);}}//--数据处理--for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {result[j][i] = arr[i][j];}}
//--输出--for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {printf("%d ", result[i][j]);}printf("\n");}
}
2.矩阵90°转置
// 颈椎病
void Demo62() {//--变量声明--// 矩阵边长, 矩阵本身, 转置后数组int size, arr[10][10], result[10][10];//--接收输入--scanf_s("%d", &size);for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {scanf_s("%d", &arr[i][j]);}}
//--数据处理--for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {result[j][size - i - 1] = arr[i][j];}}
//--输出--for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {printf("%d ", result[i][j]);}printf("\n");}
}详细分析:
//数组下标变化:假设size为30 1 2 0 1 2 31 4 5 6 2 7 8 9->0 1 2 0 7 4 11 8 5 2 2 9 6 3x1 y y x2
[0][0]->[0][2]
[0][1]->[1][2]
[1][2]->[2][1]
[2][1]->[1][0]//规律:
x转y ,y转x
x转y时 size - x = y,由于下标开始值为0,所以size - 1 - x = y
y转x时 y = x
如上,y下标原封替换x坐标,但是x下标需要被size - 1 减后才能作为新数组的y下标。3.杨辉三角
#include<iostream>
using namespace std;
void Print(int n, int a[][10]);
void YH(int n)
{int a[10][10];//计算杨辉三角, 以下三角矩阵的形式存放在二维数组for (int i = 0; i < n; i++) {a[i][0] = 1;a[i][i] = 1;for (int j = 1; j < i; j++)a[i][j] = a[i - 1][j - 1] + a[i - 1][j]; //i不可能取值为0导致地址越界 }Print(n,a);
}
void Print(int n,int a[][10])
{for (int i = 0; i < n; i++) {for (int j = 1; j <= n - 1 - i; j++) //打印每行开始的空格 cout << " ";for (int j = 0; j <= i; j++) //每行打印的数据个数cout << a[i][j] << " ";cout << endl;}
}
int main() {int n; cin >> n;YH(n);system("pause"); return 0;
}
// 杨辉三角
void Demo63() {//--变量声明--// 杨辉三角的高度int n;// 存储用数组, 注意杨辉三角只会占用一半的空间, 所以这里可以用malloc动态分配来避免空间浪费int arr[10][10];//--接收输入--scanf_s("%d", &n);arr[0][0] = 1;
//--数据处理--// 左右两侧数据直接填充即可for (int i = 1; i < n; i++) {arr[i][0] = arr[i][i] = 1;for (int j = 1; j < i; j++) {arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}//--输出--for (int i = 0; i < n; i++) {for (int j = 0; j <= i; j++) {printf("%d ", arr[i][j]);}printf("\n");}
}
4.包围圈
// 包围圈
void Demo64() {//--变量声明--int size, tree[10][10];// 当前坐标xy, 移动方向toward 0左 1下 2右 3上, 填充数// 注意 由于第一次探查前会先移动 x++ 所以x需要修正为-1int x = -1, y = 0, toward = 0, num = 0;// 一个方向的移动步数int s;
//--接收输入--scanf_s("%d", &size);s = size;
//--数据处理--// 移动规律 如果是4 则是4+3+3+2+2+1+1 = 16 同理 如果是5 5+4+4+3+3+2+2+1+1// 外部循环: 每奇数次循环, 最大步数-1. 一个方向移动完后 对方向进行修改// 内部循环: 循环(步数)次, 每次移动根据方向对xy进行修改
for (int i = 0; num<size*size; i++) {// 奇数次循环 最大步数-1if (i % 2 == 1) s--;for (int j = 0; j < s; j++) {// 获取方向并移动switch (toward) {case 0:x++;break;case 1:y++;break;case 2:x--;break;case 3:y--;break;}tree[y][x] = ++num;}
// 改变方向 注意 当toward为3 也就是向上时, 需要取模操作 也就是变为0// (1+1) %4 = 2 (3+1) %4=0toward = (toward + 1) % 4;}
//--输出--for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {printf("%d ", tree[i][j]);}printf("\n");}
}
相关文章:

C/CPP基础练习题多维数组,矩阵转置,杨辉三角详解
多维数组 1. 矩阵转置 输入一个数字构成的矩形, 将矩形的值进行转置后打印 输入: 第一行 正整数n(1<n<10), 表示矩阵的边长 随后输入一个矩阵 输出: 转置后的矩阵 样例输入: 3 1 2 3 4 5 6 7 8 9 样例输出: 1 4 7 2 5 8 3 6 9 2. 颈椎病治疗 最近云海学长一…...
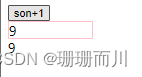
父组件用ref获取子组件数据
子组件 Son/index.vue 子组件的数据和方法一定要记得用defineExpose暴露,不然父组件用ref是获取不到的!!! <script setup> import { ref } from "vue"; const sonNum ref(1); const changeSon () > {sonNum.…...

Haskell添加HTTP爬虫ip编写的爬虫程序
下面是一个简单的使用Haskell编写的爬虫程序示例,它使用了HTTP爬虫IP,以爬取百度图片。请注意,这个程序只是一个基本的示例,实际的爬虫程序可能需要处理更多的细节,例如错误处理、数据清洗等。 import Network.HTTP.Cl…...
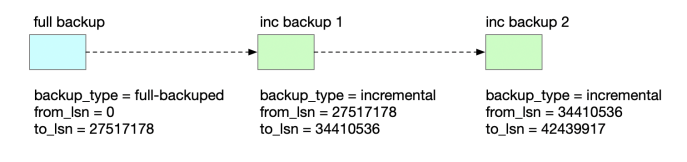
MySQL 社区开源备份工具 Xtrabackup 详解
文章目录 前言1. Xtrabackup 介绍1.1 物理备份与逻辑备份区别1.2 Xtrabackup 系列版本 2. Xtrabackup 部署2.1 下载安装包2.2 二进制部署2.3 程序文件介绍2.4 备份需要的权限 3. Xtrabackup 使用场景3.1 本地全量备份3.2 本地压缩备份3.3 全量流式备份3.3.1 备份到远程主机3.3.…...
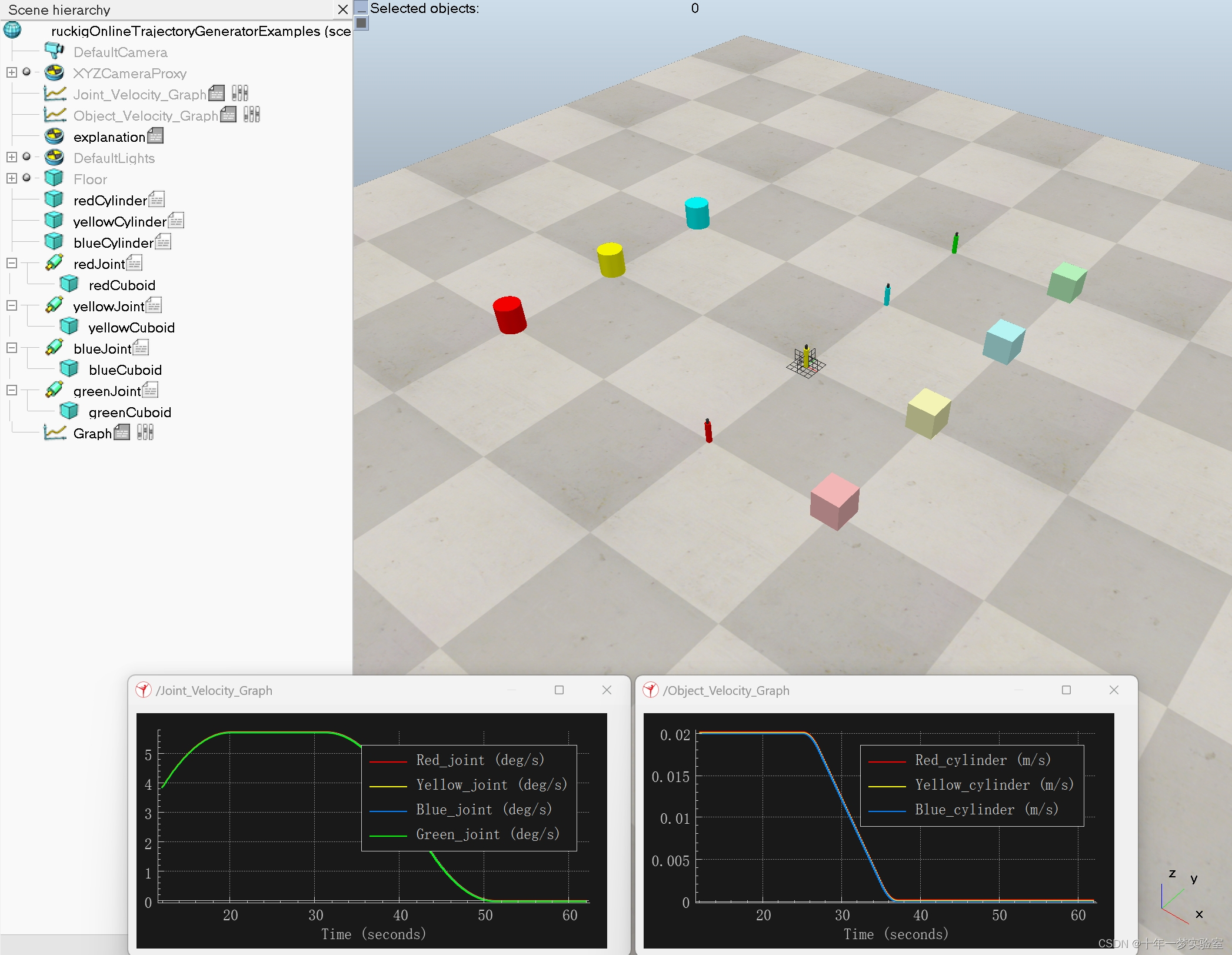
【仿真】ruckig在线轨迹生成器示例
该场景说明了使用 CoppeliaSim 中提供的 Ruckig 在线轨迹生成功能的各种方法: 1. 在线程脚本内使用单个阻塞函数(红色) 2. 在线程脚本中使用多个非阻塞函数(黄色) 3. 在非线程脚本中使用多个非阻塞函数(…...

LeetCode 面试题 16.22. 兰顿蚂蚁
文章目录 一、题目二、C# 题解 一、题目 一只蚂蚁坐在由白色和黑色方格构成的无限网格上。开始时,网格全白,蚂蚁面向右侧。每行走一步,蚂蚁执行以下操作。 (1) 如果在白色方格上,则翻转方格的颜色,向右(顺时针)转 90 度…...
Docker安装详细步骤及相关环境安装配置(mysql、jdk、redis、自己的私有仓库Gitlab 、C和C++环境以及Nginx服务代理)
目录 一、从空白系统中克隆Centos7系统 二、使用xshell连接docker_tigerhhzz虚拟机编辑 三、在CentOS7基础上安装Docker容器 四、在Docker中进行安装Portainer 4.1、在Docker中安装MySQL 4.2、在Docker中安装JDK8,安装Java环境 4.3、Docker安装redis&#…...
科研学习|研究方法——Python计量Logit模型
一、离散选择模型 莎士比亚曾经说过:To be, or not to be, that is the question,这就是典型的离散选择模型。如果被解释变量时离散的,而非连续的,称为“离散选择模型”。例如,消费者在购买汽车的时候通常会比较几个不…...

灵活运用Vue指令:探究v-if和v-for的使用技巧和注意事项
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、作…...

nvidia-docker部署pytorch服务【GPU工作站】
文章目录 一、安装 Docker二、安装 NVIDIA Container Toolkit三、宿主机安装 cuda 和 nvidia-driver四、测试一、安装 Docker 可以参考这篇文章 https://blog.csdn.net/weixin_43721000/article/details/124237932 二、安装 NVIDIA Container Toolkit 参考nvidia官方 https:/…...
单链表的实现
CSDN主页:醋溜马桶圈_C语言进阶,初始C语言,数据结构-CSDN博客 Gitee主页:mnxcc (mnxcc) - Gitee.com 专栏:数据结构_醋溜马桶圈的博客-CSDN博客 目录 1.认识单链表 2.创建单链表 3.单链表的操作 3.1打印单链表 3.2开辟新空间 3.3尾插 3.4头插…...
)
【python】面向对象(类型定义魔法方法)
目录 一、引言 二、类型定义 1、什么是类型的定义? 2、案例 三、魔法方法 1、什么是魔法方法 2、基础部分 3、比较操作 4、容器类型 5、属性管理 6、封装 7、方法拓展 8、继承 9、多态 一、引言 Python是一种面向对象的语言,它支持类&#…...
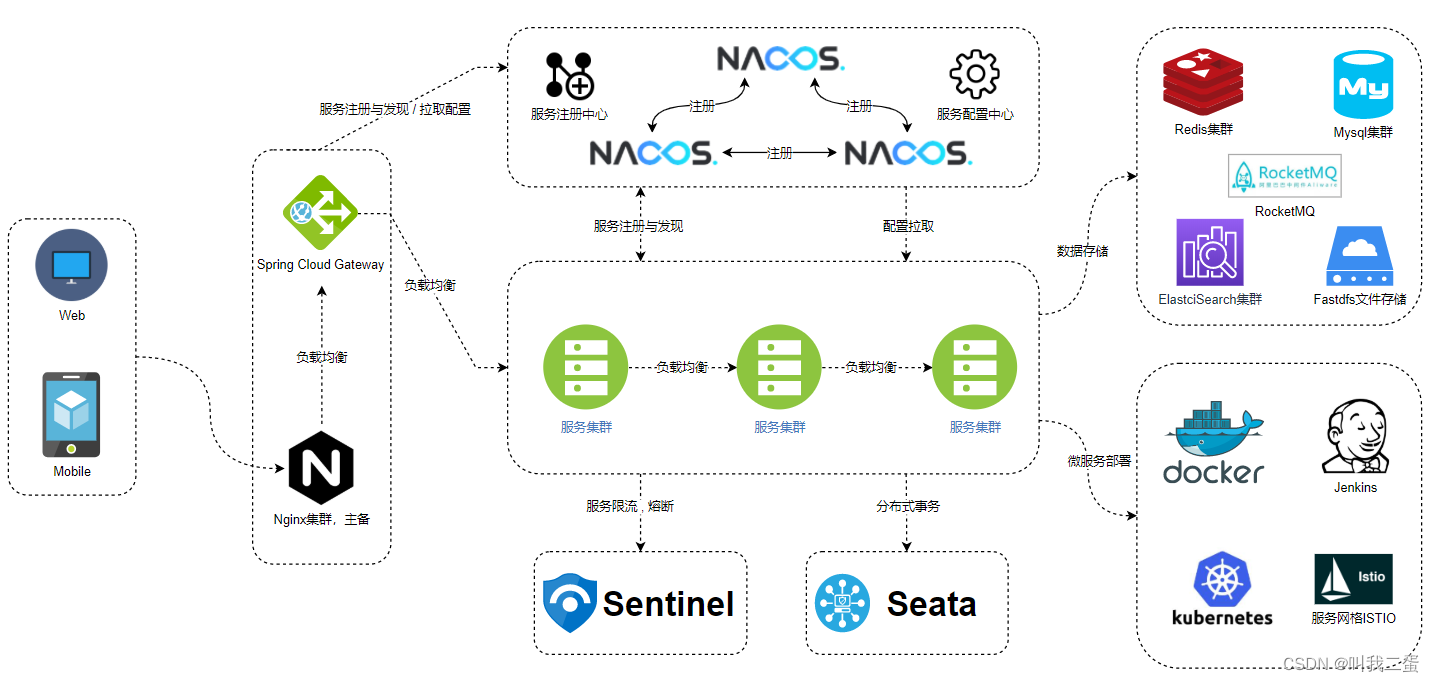
1.微服务与SpringCloud
微服务和SpringCloud 文章目录 微服务和SpringCloud1.什么是微服务2.SpringCloud3. 微服务 VS SpringCloud4. SpringCloud 组件5.参考文档6.版本要求 1.什么是微服务 微服务是将一个大型的、单一的应用程序拆分成多个小型服务,每个服务实现特定的业务功能ÿ…...
【2023全网最全最火】Selenium WebDriver教程(建议收藏)
在本教程中,我将向您介绍 Selenium Webdriver,它是当今市场上使用最广泛的自动化测试框架。它是开源的,可与所有著名的编程语言(如Java、Python、C#、Ruby、Perl等)一起使用,以实现浏览器活动的…...
)
dimp 导入dmp文件报错:无效的模式名(DM8:达梦数据库)
dimp 导入dmp文件报错:无效的模式名-DM8:达梦数据库 环境介绍1 搭建A1 数据库52361.1 A1数据库5236创建模式名,表,测试数据1.2 从A1数据库5236导出dmp文件 2 搭建A2数据库52372.1 创建 数据用户ABC2311152.2 在A2 数据库5237 导入DMP(报错无效的模式名)2.3 使用REMAP_SCHEMAABC…...
)
宿主机无法连接docker里的redis问题解决(生产环境慎用)
宿主机无法连接docker里的redis问题解决(生产环境慎用) 问题描述解决方案 问题描述 1.连接超时 2.连接能连上但马上断开并报错 3.提示保护模式什么的 (error) DENIED Redis is running in protected mode because protected mode is enabled链接redis …...
给女朋友开发个小程序低价点外卖吃还能赚钱
前言 今天又是无聊的一天,逛了下GitHub,发现一个库里面介绍美团饿了吗外卖红包外卖优惠券,先领红包再下单。外卖红包优惠券,cps分成,别人领红包下单,你拿佣金。哇靠,那我岂不是可以省钱还可以赚钱,yyds。。。。想想都美好哈哈哈!!! 回到正题,这个是美团饿了么分销…...

外贸客户管理系统是什么?推荐的管理软件?
外贸客户管理系统哪个好用?海洋建站如何选管理系统? 外贸客户管理系统,是一款专为外贸企业设计的客户关系管理系统,旨在帮助外贸企业建立与维护客户关系,提高客户满意度和忠诚度,提升企业业绩。海洋建站将…...

数据挖掘:分类,聚类,关联关系,回归
数据挖掘: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤其sql要学&…...

力扣labuladong一刷day10一网打尽股票买卖问题共6题
力扣labuladong一刷day10股票买卖问题共6题 一、121. 买卖股票的最佳时机 题目链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 思路:只能买入1次,定义dp[i][0]数组表示第i天持有股票时手中的最大金额 数,…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
