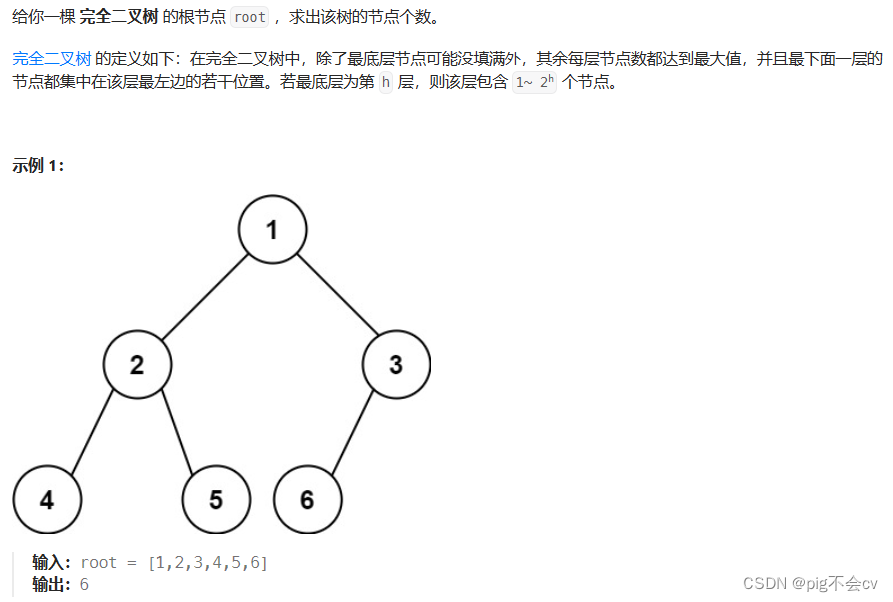
6.8完全二叉树的节点个数(LC222-E)
算法:
如果不考虑完全二叉树的特性,直接把完全二叉树当作普通二叉树求节点数,其实也很简单。
递归法:
用什么顺序遍历都可以。
比如后序遍历(LRV):不断遍历左右子树的节点数,最后加上根节点的节点数1
迭代法:
用层序遍历,改一下模版代码就行。
正确代码:
递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:if root == None:return 0#左leftnum = self.countNodes(root.left)#右rightnum = self.countNodes(root.right)#中num = 1 + leftnum + rightnumreturn num时间空间复杂度:
时间复杂度分析:
在最坏情况下,需要遍历二叉树的所有节点才能计算节点的数量。因此,时间复杂度为O(n),其中n是二叉树中的节点数。
空间复杂度分析:
递归调用的空间复杂度取决于递归的深度,即树的高度。在最坏情况下,二叉树是一个链表结构,高度为n。因此,递归调用的空间复杂度为O(n) - 此外,除了递归调用的空间,没有使用额外的数据结构。因此,除了递归调用的空间外,空间复杂度为O(1)。
综上所述,时间复杂度为O(n),空间复杂度为O(n)(由于递归调用的空间)或O(1)(除了递归调用的空间)。
相关文章:

6.8完全二叉树的节点个数(LC222-E)
算法: 如果不考虑完全二叉树的特性,直接把完全二叉树当作普通二叉树求节点数,其实也很简单。 递归法: 用什么顺序遍历都可以。 比如后序遍历(LRV):不断遍历左右子树的节点数,最后…...

基于协作mimo系统的RM编译码误码率matlab仿真,对比硬判决译码和软判决译码
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ..................................................................... while(Err < TL…...
Django模型层
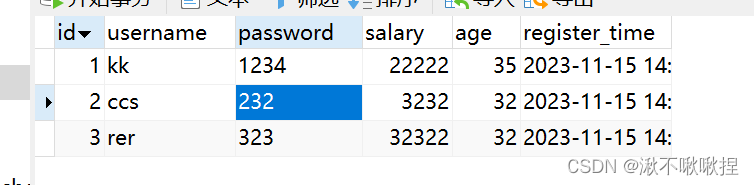
模型层 与数据库相关的,用于定义数据模型和数据库表结构。 在Django应用程序中,模型层是数据库和应用程序之间的接口,它负责处理所有与数据库相关的操作,例如创建、读取、更新和删除记录。Django的模型层还提供了一些高级功能 首…...

计算机视觉的应用18-一键抠图人像与更换背景的项目应用,可扩展批量抠图与背景替换
大家好,我是微学AI,今天给大家介绍一下计算机视觉的应用18-一键抠图人像与更换背景的项目应用,可扩展批量抠图与背景替换。该项目能够让你轻松地处理和编辑图片。这个项目的核心功能是一键抠图和更换背景。这个项目能够自动识别图片中的主体&…...

Redis(哈希Hash和发布订阅模式)
哈希是一个字符类型字段和值的映射表。 在Redis中,哈希是一种数据结构,用于存储键值对的集合。哈希可以理解为一个键值对的集合,其中每个键都对应一个值。哈希在Redis中的作用主要有以下几点: 1. 存储对象:哈希可以用…...

php正则表达式汇总
php正则表达式有"/pattern/“、”“、”$“、”.“、”[]“、”[]“、”[a-z]“、”[A-Z]“、”[0-9]“、”\d"、“\D”、“\w”、“\W”、“\s”、“\S”、“\b”、“*”、“”、“?”、“{n}”、“{n,}”、“{n,m}”、“\bword\b”、“(pattern)”、“x|y"和…...
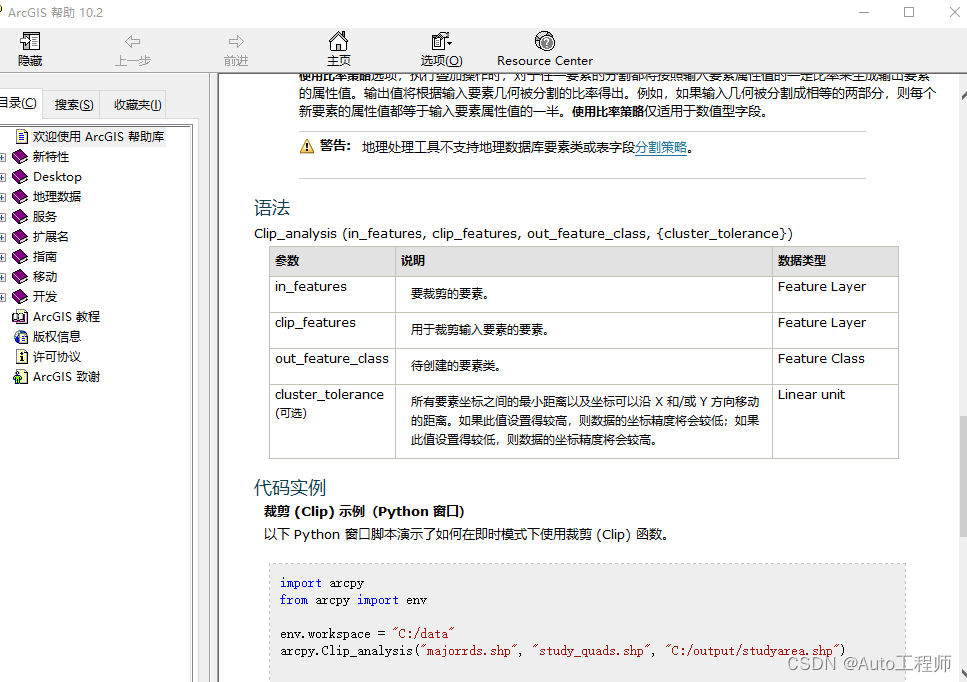
Python与ArcGIS系列(八)通过python执行地理处理工具
目录 0 简述1 脚本执行地理处理工具2 在地理处理工具间建立联系0 简述 arcgis包含数百种可以通过python脚本执行的地理处理工具,这样就通过python可以处理复杂的工作和批处理。本篇将介绍如何利用arcpy实现执行地理处理工具以及在地理处理工具间建立联系。 1 脚本执行地理处理…...
cocos----刚体
刚体(Rigidbody) 刚体(Rigidbody)是运动学(Kinematic)中的一个概念,指在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体。在 Unity3D 中ÿ…...

【SAP-HCM】--HR人员信息导入函数
人员基本信息导入函数:HR_MAINTAIN_MASTERDATA 人员其他信息类型导入函数:HR_INFOTYPE_OPERATION 不逼逼,直接上代码,这两个函数还是相对简单易懂的 *根据操作类型查找对应的T529A 操作类型对应的值IF gt_alv IS NOT INITIAL.S…...

【开源】基于JAVA的大学兼职教师管理系统
项目编号: S 004 ,文末获取源码。 \color{red}{项目编号:S004,文末获取源码。} 项目编号:S004,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容三、界面展示3.1 登录注册3.2 学生教师管…...

Pyhon函数
import time # # for i in range(1,10): # j1 # for j in range(1,i1): # print(f"{i}x{j}{i*j} " ,end) # print() #复用,代码,精简,复用度高def j99(n1,max10): for i in range(n,max):jifor j in ran…...

使用vuex完成小黑记事本案例
使用vuex完成小黑记事本案例 App.vue <template><div id"app"><TodoHeader></TodoHeader><TodoMain ></TodoMain><TodoFooter></TodoFooter></div> </template><script> import TodoMain from …...
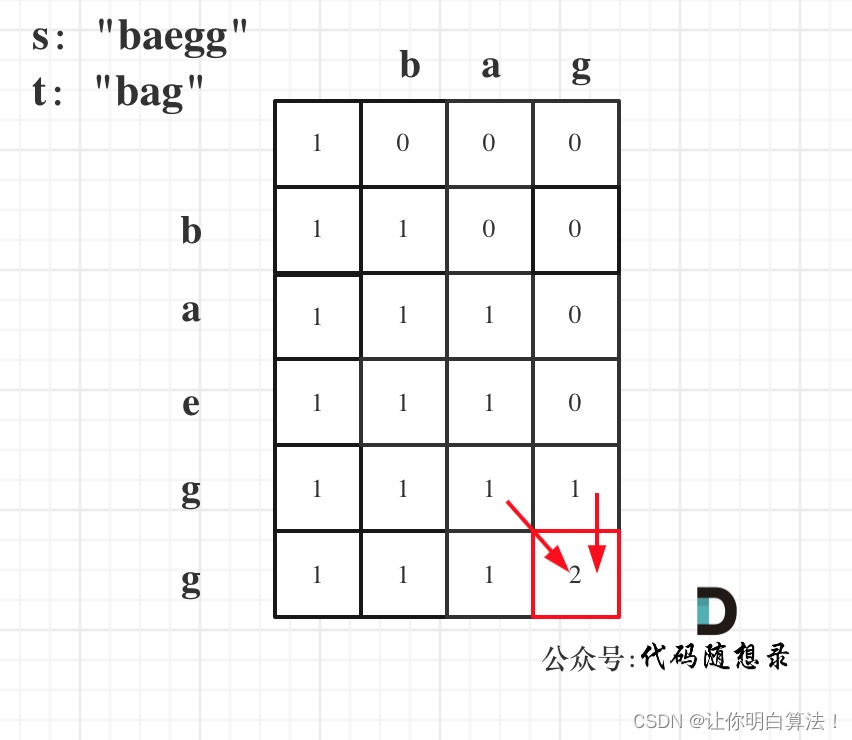
进阶理解:leetcode115.不同的子序列(细节深度)
这道题是困难题,本章是针对于动态规划解决,对于思路进行一个全面透彻的讲解,但是并不是对于基础讲解思路,而是渗透到递推式和dp填数的详解,如果有读者不清楚基本的解题思路,请看我的这篇文章算法训练营DAY5…...
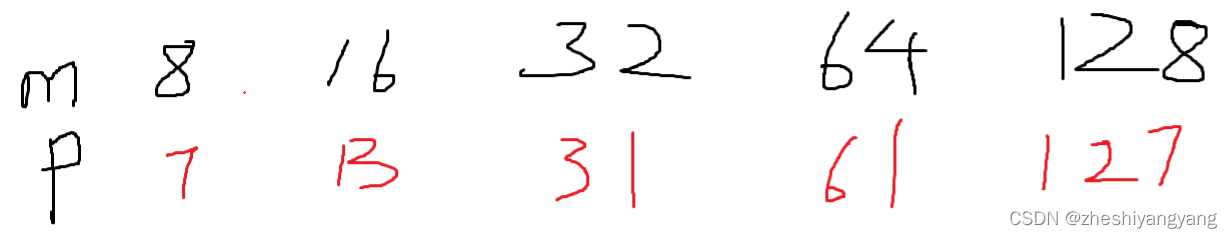
数据结构-哈希表(C语言)
哈希表的概念 哈希表就是: “将记录的存储位置与它的关键字之间建立一个对应关系,使每个关键字和一个唯一的存储位置对 应。” 哈希表又称:“散列法”、“杂凑法”、“关键字:地址法”。 哈希表思想 基本思想是在关键字和存…...
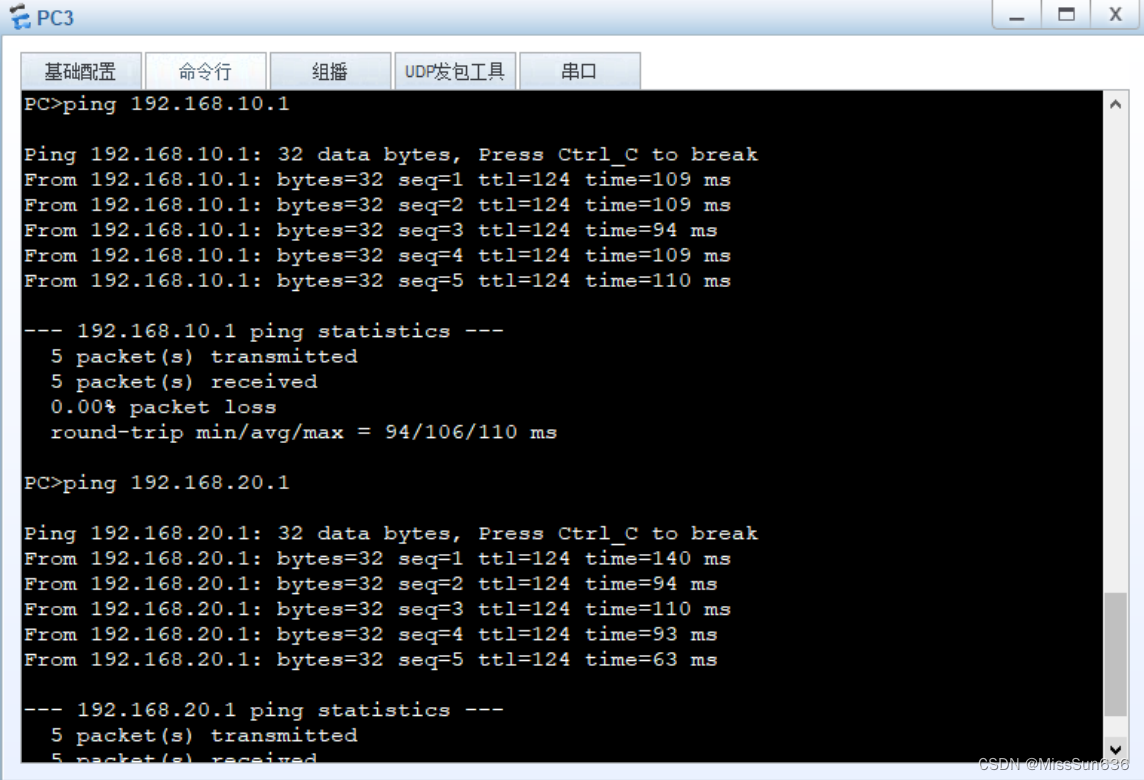
HCIA-综合实验(三)
综合实验(三) 1 实验拓扑2 IP 规划3 实验需求一、福州思博网络规划如下:二、上海思博网络规划如下:三、福州思博与上海思博网络互联四、网络优化 4 配置思路4.1 福州思博配置在 SW1、SW2、SW3 上配置交换网络SW1、SW2、SW3 运行 S…...

Java程序员的成长路径
熟悉JAVA语言基础语法。 学习JAVA基础知识,推荐阅读书单中的经典书籍。 理解并掌握面向对象的特性,比如继承,多态,覆盖,重载等含义,并正确运用。 熟悉SDK中常见类和API的使用,比如࿱…...

几种常用的排序
int[] arr new int[]{1, 2,8, 7, 5};这是提前准备好的数组 冒泡排序 public static void bubbleSort(int[] arr) {int len arr.length;for (int i 0; i < len - 1; i) {for (int j 0; j < len - i - 1; j) {if (arr[j] > arr[j1]) {int temp arr[j];arr[j] ar…...

性能测试【第三篇】Jmeter的使用
线程数:10 ,设置10个并发 Ramp-Up时间(秒):所有线程在多少时间内启动,如果设置5,那么每秒启动2个线程 循环次数:请求的重复次数,如果勾选"永远"将一直发送请求 持续时间时间:设置场景运行的时间 启动延迟:设置场景延迟启动时间 响应断言 响应断言模式匹配规则 包括…...

业务:业务系统检查项参考
名录明细云平台摸底1.原有云平台体系:VMware、openstack、ovirt、k8s、docker、混合云系列及版本 2.原有云平台规模,物理机数量、虚拟机数量、迁移业务系统所占配额 3.待补充系统摸底 (适用于物理主机)每一台虚拟机或物理机: 1.系统全局参数…...
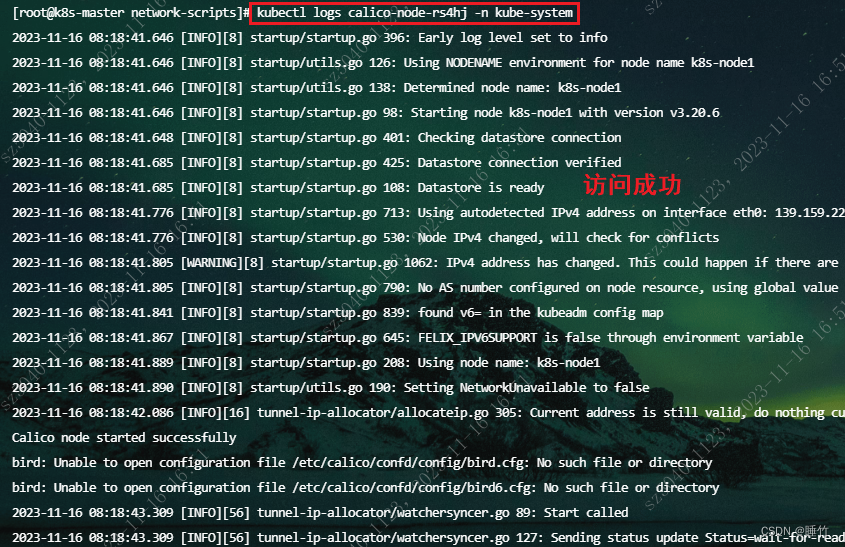
解决公网下,k8s calico master节点无法访问node节点创建的pod
目的:解决pod部署成功后,只能在node节点访问,而master节点无法访问 原因:集群搭建时,没有配置公网进行kubectl操作,从而导致系统默认node节点,使用内网IP加入k8s集群!如下ÿ…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
