当前位置：首页 > news >正文

强化学习各种符号含义解释

news 2025/10/28 2:29:50

$s,{s}'$ ：状态

$a$ : 动作

$r$ : 奖励

$R$ : 奖励函数

$S$ : 非终结状态

$S^{+}$ : 全部状态，包括终结状态

$A$ : 动作集合

ℛ : 奖励集合

$\boldsymbol{P}$ : 转移矩阵

$t$ : 离散时间步

$T$ ：回合内最终时间步

$S_t$ : 时间t的状态

$A_t$ : 时间t动作

$R_t$ : 时间t的奖励,通常为随机量，且由 $A_t$ 和 $S_t$ 决定

$G_t$ : 回报

$G_t^{(n)}$ : n步回报

$G_t^{\lambda}$ : $\lambda$ 折扣回报

$\pi$ : 策略

$\pi(s)$ : 根据确定性策略 $\pi$ , 状态s时所采取的动作

$\pi(a|s)$ : 根据随机性策略 $\pi$ , 在状态s时执行动作a的概率

$p({s}',r|s,a)$ : 根据状态s和动作a，使得状态转移成 ${s}'$ 且获得奖励r的概率

$p({s}'|s,a)$ : 根据转态s和动作a,使得状态转移成 ${s}'$ 的概率

$v_{\pi}(s)$ : 根据策略 $\pi$ ，状态s的价值(回报期望)

$v_{\star}(s)$ : 根据最优策略，状态s的价值

$q_{\pi}(s,a)$ : 动作价值函数，根据策略 $\pi$ ，在状态s时执行动作a的价值

$q_{\star}(s,a)$ : 根据最优策略，在状态s时执行动作a的价值

$V,V_t$ : 状态价值函数的估计

$Q,Q_t$ : 动作价值函数的估计

$\tau$ ： $\tau = (S_0, A_0,R_0,S_1,A_1,R_1,...)$ 状态，动作，奖励的轨迹

$\gamma$ ： $\gamma \in [0,1]$ , 奖励折扣因子

$\epsilon$ ：根据 $\epsilon$ -贪婪策略，执行随机动作的概率

$\alpha, \beta$ : 步长

$\lambda$ : 资格迹的衰减速率

$R(\tau)$ 是轨迹 $\tau$ 的 $\gamma$ -折扣化回报， $R(\tau)=\sum_{t=0}^{\infty}\gamma^{t}R_t$

$p(\tau)$ 是轨迹的概率：

$p(\tau) = \rho_0(S_0)\prod_{t=0}^{T-1}p(S_{t+1}|S_t)$ ，对于 $\rho_0(S_0)$ 是起始状态分布

$p(\tau|\pi)=\rho_0(S_0)\prod_{t=0}^{T-1}p(S_{t+1}|S_t,A_t)\pi(A_t|S_t)$ , $\rho_0(S_0)$ 是起始状态分布

$J(\pi)$ 是策略 $\pi$ 的期望回报， $J(\pi)=\int_{\tau}p(\tau|\pi)R(\tau)=\mathbb{E}_{\tau\sim\pi}[R(\tau)]$ : 对于这个公式的理解为策略 $\pi$ 可以产生很多轨迹 $\tau$ ,产生每个轨迹的概率为 $p(\tau|\pi)$ ,而每个轨迹 $\tau$ 的奖励为 $R(\tau)$ ,所以总的策略 $\pi$ 可以获得的奖励的期望就是所有轨迹的概率乘与该轨迹的奖励的积分。对于右边期望描述的就是对于服从策略 $\pi$ 的轨迹 $\tau$ ，求轨迹的奖励值 $R(\tau)$ 的期望。

$\pi^{\star}$ 是最优策略，最优策略就是能够获得最大的策略期望的策略，即为 $\pi^{\star}=arg max_{\pi}J(\pi)$

$v_{\pi}(s)$ 是状态s在策略 $\pi$ 下的价值，也就是这个状态能够获得的期望回报。

$v_{\star}(s)$ 是状态s在最优策略 $\pi$ 下的价值，也就是这个状态能够在最优策略下获得的期望回报，最终都转化为了奖励的计算。

$q_{\pi}(s,a)$ 是状态s在策略 $\pi$ 下执行动作a的价值（期望回报）

$q_{\star}(s,a)$ 是状态s在最优策略下执行动作a的价值（期望回报）

$V(s)$ 是对MRP（Markov Reward Process）中从状态s开始的状态价值的估计

$V^{\pi}(s)$ 是对MDP（Markov Decision Process）中在线状态价值函数的估计，给定策略 $\pi$ ,有期望回报：

$V^{\pi}(s)\approx v_{\pi}(s)=\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s]$

其中MP，MRP，MDP参考：MP、MRP、MDP（第二节） - 知乎 (zhihu.com)

$Q^{\pi}(s,a)$ 是对MDP下在线动作价值函数的估计，给定策略 $\pi$ ，有期望回报：

$Q^{\pi}(s,a)\approx q_{\pi}(s,a)=\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s,A_0=a]$

$V^{\star}(s)$ 是对MDP下最优动作价值函数的估计，根据最优策略，有期望回报：

$V^{\star}(s)\approx v_{\star}(s) = max_{\pi}\mathbb{E}_{\tau\sim\pi}[R(\tau)|S_0=s]$

$Q^{\star}(s,a)$ 是对MDP下最优动作价值函数的估计，根据最优策略，有期望回报：

$Q^{\star}(s,a)\approx q_{\star}(s,a) = max_{\pi}\mathbb{E}_{\tau \sim\pi}[R(\tau)|S_0=s,A_0=a]$

$A^{\pi}(s,a)$ 是对状态s和动作a的优势估计函数：

$A^{\pi}(s,a)=Q^{\pi}(s,a) - V^{\pi}(s)$

在线状态价值函数 $v_{\pi}(s)$ 和在线动作价值函数 $q_{\pi}(s,a)$ 的关系：

$v_{\pi}(s)=\mathbb{E}_{a\sim\pi}[q_{\pi}(s,a)]$

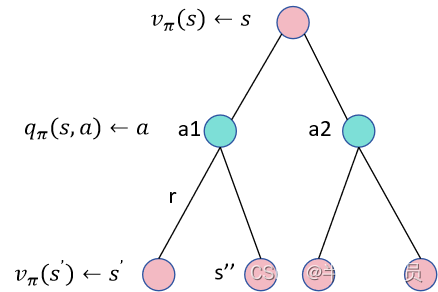
如上图所示：状态s对应多个动作a1,a2，执行一个动作之后，又可能转移到多个状态中去，所以 $v_{\pi}(s)$ 的值就是在状态s之下能够采取的所有动作的动作价值函数的期望，即为

$v_{\pi}(s)=\mathbb{E}_{a\sim\pi}[q_{\pi}(s,a)]$

另一种写法：

$v_{\pi}(s)=\sum_{a \in A}\pi(a|s)q_{\pi}(s,a)$

这里写的是 $v_{\pi}(s)$ 和 $q_{\pi}(s,a)$ 之间的关系，同理另外一种转换关系是，执行一个动作之后得到的及时奖励值+下一个状态的状态价值函数的折扣，即为

$v_{\pi}(s)=\sum_{a\in A}\pi(a|s)(R_s^a+\gamma\sum_{s'\in S}P_{ss'}^av_{\pi}(s'))$ ,

$P_{ss'}^a$ 是在状态s执行动作a转移到s'的概率，这样就把 $v_{\pi}(s)$ 和 $v_{\pi}(s')$ 关联起来了。另一种写法如下：

$v_{\pi}(s)=\mathbb{E}_{a\sim \pi(\cdot |s),s'\sim p(\cdot |s,a)}[R(s,a)+\gamma v_{\pi}(s')]$

最优状态价值函数 $v_{\star}(s)$ 和最优动作价值函数 $q_{\star}(s,a)$ 的关系是：

$v_{\star}(s)=max_{a}q_{\star}(s,a)$

上面的公式很好理解，在最优策略下，给一个状态s，这个策略肯定能够选到最好的动作去执行，那么当前状态的价值函数就不是去求所有动作价值函数的期望了，而是就等于动作价值函数最大的那个值。

$a_{\star}(s)$ 是在最优策略下，状态s执行的最优动作

$a_{\star}(s)=argmax_{a}q_{\star}(s,a)$

在线动作价值函数的贝尔曼方程：

$q_{\pi}(s,a)=\mathbb{E}_{s' \sim p(\cdot |s,a)}[R(s,a)+\gamma\mathbb{E}_{a' \sim \pi(\cdot|s')}[q_{\pi}(s',a')]]$

另外一种写法是：

$q_{\pi}(s,a)=R_s^a+\gamma\sum_{s' \in S}p_{ss'}^{a}\sum_{a' \in A}\pi(a'|s')q_{\pi}(s',a')$

上面是 $q_{\pi}(s,a)$ 和 $q_{\pi}(s',a')$ 的关系，下面是 $q_{\pi}(s,a)$ 和 $v_{\pi}(s')$ 的关系：

$q_{\pi}(s,a)=R_s^a+\gamma\sum_{s' \in S}P_{ss'}^av_{\pi}(s')$

另外一种写法是：

$q_{\pi}(s,a)=R_s^a+\gamma\mathbb{E}_{s' \sim p(\cdot|s,a)}[v_{\pi}(s')]$

最优状态价值函数的贝尔曼方程：

$v_{\star}(s)=max_a \mathbb{E}_{s' \sim p(\cdot | s,a)}[R(s,a)+\gamma v_{\star}(s')]$

另外一种写法是：

$v_{\star}(s)=max_aR_s^a+\gamma \sum_{s' \in S}P_{ss'}^av_{\star}(s')$

最优动作价值函数的贝尔曼方程：

$q_{\star}(s,a)=\mathbb{E}_{s' \sim p(\cdot |s,a)}[R(s,a)+\gamma max_{a'}q_{\star}(s',a')]$

另外一种写法是：

$q_{\star}(s,a)=R_s^a+\gamma \sum_{s' \in S}P_{ss'}^amax_{a'}q_{\star}(s',a')$

相关文章：

强化学习各种符号含义解释

：状态 : 动作 : 奖励 : 奖励函数 : 非终结状态 : 全部状态，包括终结状态 : 动作集合 ℛ : 奖励集合 : 转移矩阵 : 离散时间步 ： 回合内最终时间步 : 时间t的状态 : 时间t动作 : 时间t的奖励,通常为随机量，且由和决定 : 回报 : n步…...

编程日记 2023/11/18 17:48:50

Axure基础详解二十：中继器随机抽奖效果

效果演示组件一、中继器建立一个“中继器”内部插入一个“正方形”，给“正方形”添加一个【样式效果】>>【选中状态】填充背景为红色，字体白色。在中继器表格中插入两列数据函数：【xuhao】(序号列，按12345……填写&…...

编程日记 2023/11/18 17:47:49

企业信息化与电子商务＞供应链信息流

1.供应链信息流概念供应链信息流是指整个供应链上信息的流动。它是一种虚拟形态，包括了供应链上的供需信息和管理信息，它伴随着物流的运作而不断产生。因此有效的供应链管理作为信息流的管理主要作用在于及时在供应链中传递需求和供给信息，…...

编程日记 2023/11/18 17:46:48

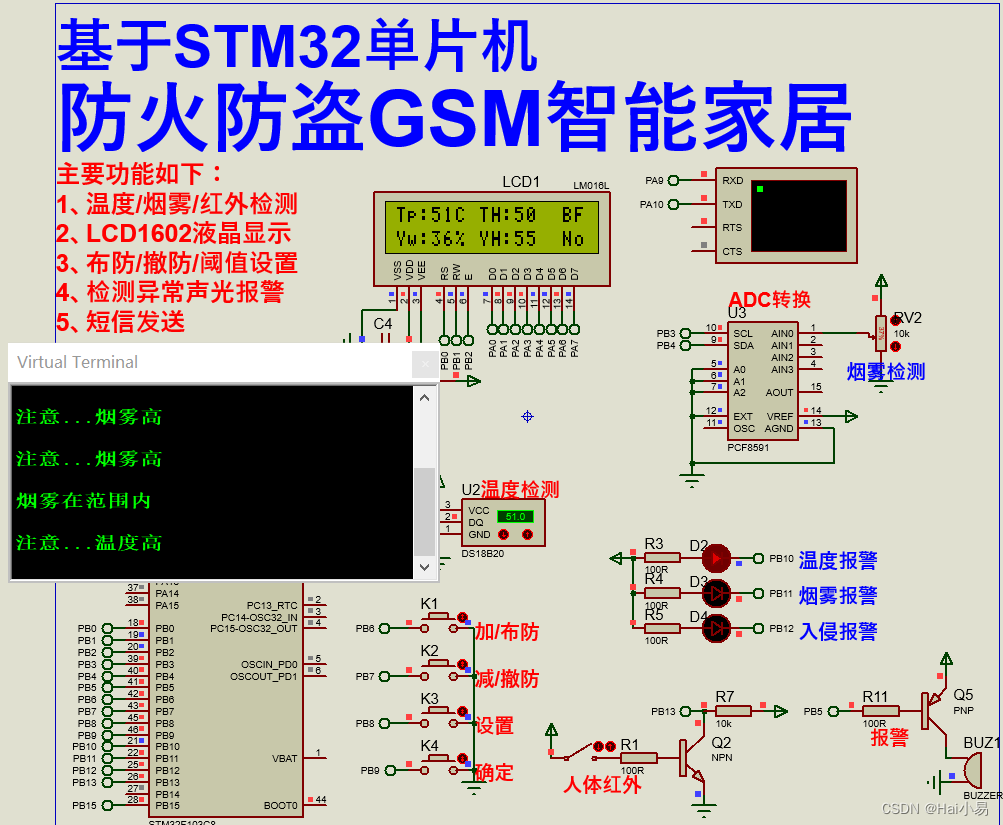
【Proteus仿真】【STM32单片机】防火防盗GSM智能家居设计

文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介本项目使用Proteus8仿真STM32单片机控制器，使用声光报警模块、LCD1602显示模块、DS18B20温度、烟雾传感器模块、按键模块、PCF8591 ADC模块、红外检测模块等。主要功能： 系统运行…...

编程日记 2023/11/18 17:45:47

快速入门ESP32——开发环境配置PlatformIO IDE

相关文章快速入门ESP32——开发环境配置Arduino IDE 快速入门ESP32——开发环境配置PlatformIO IDE 一、下载安装二、验证一、下载安装下载安装 vscode 安装PlatformIO插件创建工程二、验证写一个简单的函数来验证一下功能 void setup() {// put your setup cod…...

编程日记 2023/11/18 17:44:46

Oxygen XML Editor 26版新功能

▲ 搜索“大龙谈智能内容”关注GongZongHao▲ 2023年10月26日，罗马尼亚SyncRO Soft公司发布Oxygen XML Editor、Oxygen Web Author和Oxygen Publish Engine 26版本。 1. Oxygen XML Editor 26新功能简介 AI助手帮助写作者通过执行重复任务、审查语法、生成结构…...

编程日记 2023/11/18 17:43:45

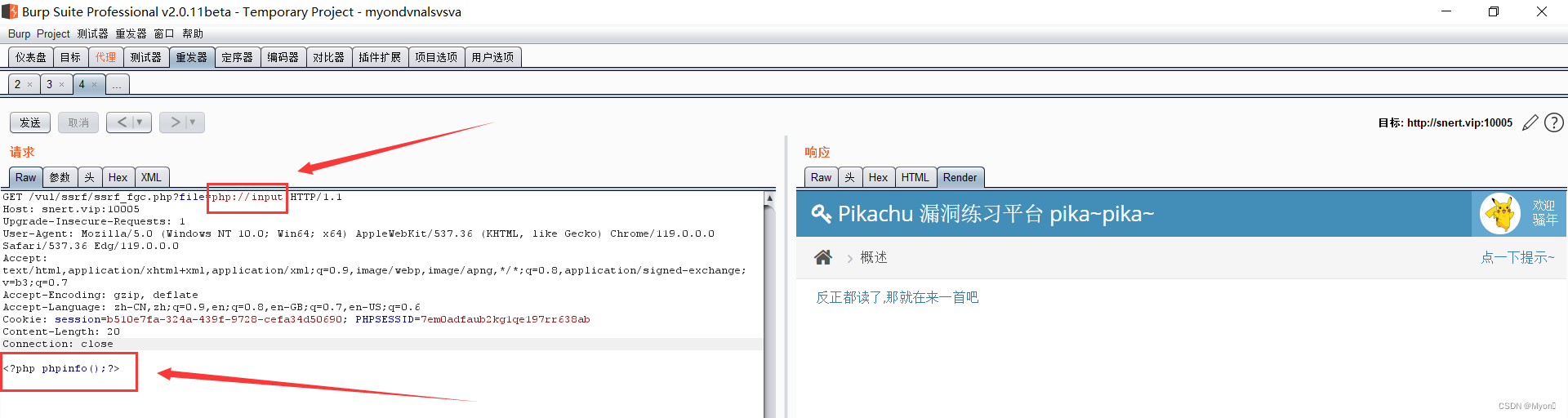
Pikachu漏洞练习平台之SSRF(服务器端请求伪造)

注意区分CSRF和SSRF： CSRF：跨站请求伪造攻击，由客户端发起； SSRF：是服务器端请求伪造，由服务器发起。 SSRF形成的原因大都是由于服务端提供了从其他服务器应用获取数据的功能，但又没有对目标…...

编程日记 2023/11/18 17:42:44

WPF异步编程

在WPF应用程序中进行异步编程是非常重要的，因为这有助于保持用户界面的响应性，特别是当执行长时间运行的操作时，例如访问网络资源、进行大量的数据处理或调用耗时的I/O操作。 WPF的异步编程通常围绕以下几个关键概念： Dispatcher…...

编程日记 2023/11/18 17:41:44

同态加密定义，四大发展阶段总结，FHE系统正式定义-全同态加密

目录同态加密定义为什么采用电路模型？四大发展阶段总结 FHE系统正式定义...

编程日记 2023/11/18 17:39:42

网上的搜索

Internet中蕴含的信息资源非常丰富，但如何在这浩瀚如海的信息空间内快速找到自己所需要的资源呢?我们需要借助于搜索引擎。在网络上，提供搜索功能的网站非常多，如百度、谷歌、搜狗等，另外有一些门户网站也提供了搜索功能&#xf…...

编程日记 2023/11/18 17:38:41

【算法-哈希表2】快乐数和两数之和

今天，带来哈希表相关算法的讲解。文中不足错漏之处望请斧正！ 理论基础点这里 1. 快乐数分析题意出题者已经把题意明确告诉我们了: 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1&am…...

编程日记 2023/11/18 17:37:40

MR外包团队：MR、XR混合现实技术应用于游戏、培训，心理咨询、教育成为一种创新的各行业MR、XR形式！

随着VR、AR、XR、MR混合现实等技术逐渐应用于游戏开发、心理咨询、培训、教育各个领域，为教育、培训、心理咨询等行业带来了全新的可能性。MR、XR游戏开发、心理咨询是利用虚拟现实技术模拟真实场景，让学生身临其境地参与学习和体验，从而提高…...

编程日记 2023/11/18 17:36:39

【P1008 [NOIP1998 普及组] 三连击】

[NOIP1998 普及组] 三连击题目背景本题为提交答案题，您可以写程序或手算在本机上算出答案后，直接提交答案文本，也可提交答案生成程序。题目描述将 1 , 2 , … , 9 1, 2, \ldots , 9 1,2,…,9 共 9 9 9 个数分成 3 3 3 组&#xff…...

编程日记 2023/11/18 17:33:33

机器学习算法——集成学习

目录 1. Bagging 1. Bagging Bagging（bootstrap aggregating：自举汇聚法）也叫装袋法，其思想是通过将许多相互独立的学习器的结果进行结合，从而提高整体学习器的泛化能力，是一种并行集成学习方法。工作流…...

编程日记 2023/11/18 17:32:32

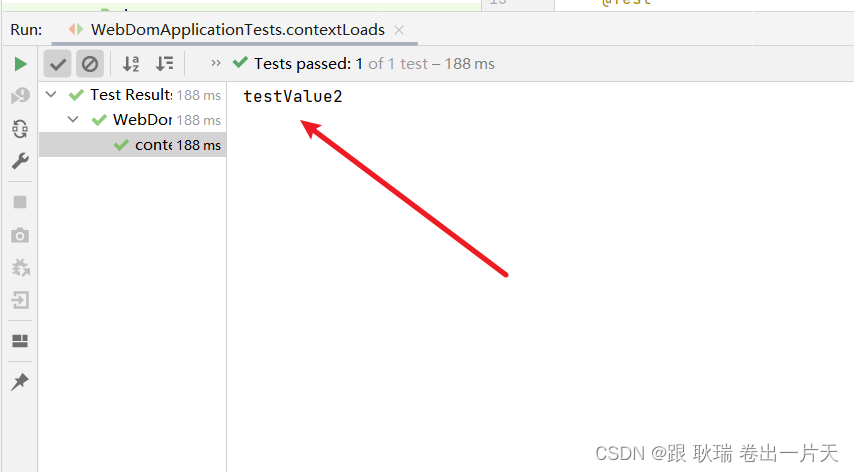
java springboot在当前测试类中添加临时属性不影响application和其他范围

目前我们的属性基本都写在 application.yml 里面了但是如果我们只是想做一下临时变量的测试有没有办法实现呢？ 显然是有的这里我们还是先在application.yml中去写一个 test属性下面加个prop 然后我们尝试在测试类中获取一下这个属性直接用 Value 读取…...

编程日记 2023/11/18 17:31:32

原型网络Prototypical Network的python代码逐行解释，新手小白也可学会！！由于工作量大，准备整8个系列完事，-----系列5

文章目录前言一、原始程序---计算原型，开始训练，计算损失二、每一行代码的详细解释2.1 粗略分析2.2 每一行代码详细分析前言承接系列4，此部分属于原型类中的计算原型，开始训练，计算损失函数。一、原始程序—计算原…...

编程日记 2023/11/18 17:30:30

milvus数据库的数据管理-插入数据

一、插入数据 1.准备数据数据必须与数据库中定义的字段元数据一致，与集合的模式匹配 import random data [[i for i in range(2000)],[str(i) for i in range(2000)],[i for i in range(10000, 12000)],[[random.random() for _ in range(2)] for _ in range(2…...

编程日记 2023/11/18 17:28:29

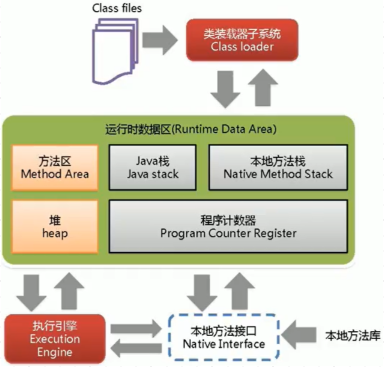
系列一、请谈谈你对JVM的理解？Java8的虚拟机有什么更新？

一、请谈谈你对JVM的理解？Java8的虚拟机有什么更新？ JVM是Java虚拟机的意思。它是建立在操作系统之上的，由类加载器子系统、本地方法栈、Java栈、程序计数器、方法区、堆、本地方法库、本地方法接口、执行引擎组成。 （1&#xff0…...

编程日记 2023/11/18 17:27:27

恕我直言，大模型对齐可能无法解决安全问题，我们都被表象误导了

是否听说过“伪对齐”这一概念？ 在大型语言模型（LLM）的评估中，研究者发现了一个引人注目的现象：当面对多项选择题和开放式问题时，模型的表现存在显著差异。这一差异根源在于模型对复杂概念的理解不够全面&…...

编程日记 2023/11/18 17:26:25

Apache Airflow (九) ：Airflow Operators及案例之BashOperator及调度Shell命令及脚本

🏡 个人主页：IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主：加入大数据技术讨论群聊，获取更多大数据资料。 🔔 博主个人B栈地址：豹哥教你大数据的个人空间-豹…...

编程日记 2023/11/18 17:25:24

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分）《Learning Humanoid Standing-up Control across Diverse Postures》系列文章：论文深度解读 + 算法与代码分析（二）作者机构：上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学论文主题：人形机器人…...

编程新知 2025/8/4 18:55:37

css实现圆环展示百分比，根据值动态展示所占比例

代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

编程新知 2025/10/27 0:02:30

爬虫基础学习day2

# 爬虫设计领域工商：企查查、天眼查短视频：抖音、快手、西瓜 ---> 飞瓜电商：京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空：抓取所有航空公司价格 ---> 去哪儿自媒体：采集自媒体数据进…...

编程新知 2025/10/17 17:04:15

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。您还将了解如何分析列，以便知晓哪些列包含有价值的数据，…...

编程新知 2025/10/24 7:46:27

Git常用命令完全指南：从入门到精通

Git常用命令完全指南：从入门到精通一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

编程新知 2025/10/3 0:40:01

Qt 事件处理中 return 的深入解析

Qt 事件处理中 return 的深入解析在 Qt 事件处理中，return 语句的使用是另一个关键概念，它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。核心区别：不同层级的事件处理方…...

编程新知 2025/6/10 21:19:52

零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程

STM32F1 本教程使用零知标准板（STM32F103RBT6）通过I2C驱动ICM20948九轴传感器，实现姿态解算，并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化，适合嵌入式及物联网开发者。在基础驱动上新增…...

编程新知 2025/10/24 21:55:02

Python 训练营打卡 Day 47

注意力热力图可视化在day 46代码的基础上，对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/10/26 9:51:09

协议转换利器，profinet转ethercat网关的两大派系，各有千秋

随着工业以太网的发展，其高效、便捷、协议开放、易于冗余等诸多优点，被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口，具有实时性、开放性，使用TCP/IP和IT标准，符合基于工业以太网的…...

编程新知 2025/10/19 3:20:06

上位机开发过程中的设计模式体会(1)：工厂方法模式、单例模式和生成器模式

简介在我的 QT/C 开发工作中，合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式：工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景在我的 QT 项目中曾经有一个需…...

编程新知 2025/8/18 3:01:22