《视觉SLAM十四讲》-- 后端 2
文章目录
- 09 后端 2
- 9.1 滑动窗口滤波和优化
- 9.1.1 实际环境下的 BA 结构
- 9.1.2 滑动窗口法
- 9.2 位姿图
- 9.2.1 位姿图的意义
- 9.2.2 位姿图优化
09 后端 2
9.1 滑动窗口滤波和优化
9.1.1 实际环境下的 BA 结构
由于计算机算力的限制,我们必须控制 BA 的规模,一种简单的思路是仅保留离当前时刻最近的 N N N 个关键帧,去掉时间上更早的关键帧。于是,BA 被固定在一个时间窗口内,离开这个窗口的即被抛弃,称为 滑动窗口法。
或者像 ORB-SLAM 2 那样,定义一种称为 共视图 的结构,即与当前相机存在共同观测的关键帧构成的图。在 BA 优化时,按照某些原则在共视图内取一些关键帧和路标进行优化。
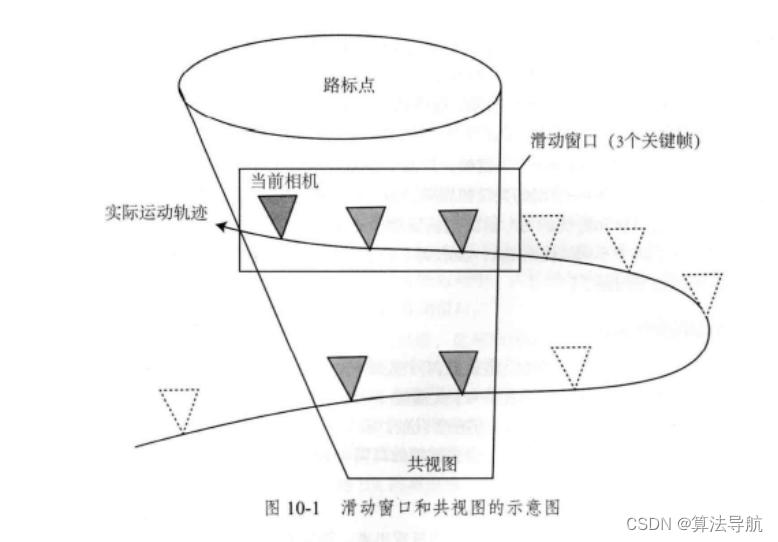
9.1.2 滑动窗口法
(1)现在考虑一个滑动窗口,假设窗口内有 N N N 个关键帧,他们的位姿表达为(李代数形式):
x 1 , x 2 , . . . , x N \boldsymbol{x}_1, \boldsymbol{x}_2,...,\boldsymbol{x}_N x1,x2,...,xN
假设这个滑动窗口中还有 M M M 个路标点 y 1 , y 2 , . . . , y M \boldsymbol{y}_1, \boldsymbol{y}_2,...,\boldsymbol{y}_M y1,y2,...,yM,用上一讲中的 BA 方法来处理这个滑动窗口,包括建立图优化模型,构建海森矩阵,在边缘化所有路标点来加速求解。边缘化时,考虑关键帧的位姿:
[ x 1 , … , x N ] T ∼ N ( [ μ 1 , … , μ N ] T , Σ ) (9-1) \left[\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\right]^{\mathrm{T}} \sim N\left(\left[\boldsymbol{\mu}_{1}, \ldots, \boldsymbol{\mu}_{N}\right]^{\mathrm{T}}, \boldsymbol{\Sigma}\right) \tag{9-1} [x1,…,xN]T∼N([μ1,…,μN]T,Σ)(9-1)
其中 μ k \boldsymbol{\mu}_k μk 为第 k k k 个关键帧的位姿均值, Σ \boldsymbol{\Sigma} Σ 为所有关键帧的协方差矩阵。显然,均值部分就是 BA 迭代之后的结果, Σ \boldsymbol{\Sigma} Σ 是对整个 BA 的 H \boldsymbol{H} H 矩阵进行边缘化之后的结果。
(2)当窗口结构改变时:
① 先在窗口中新增一个关键帧,以及观测到的路标点;
② 把窗口中一个旧的关键帧删除,可能会删除他观测到的路标点。
- 新增一个关键帧和路标点
将新的关键帧 x N + 1 \boldsymbol{x}_{N+1} xN+1 按照正常的 BA 流程处理即可。
- 删除一个旧的关键帧
删除旧的关键帧时,就比较麻烦。比如删除 x 1 \boldsymbol{x}_1 x1 ,但 x 1 \boldsymbol{x}_1 x1 并不是孤立的,它会和其它帧观测到同样的路标,将 x 1 \boldsymbol{x}_1 x1 边缘化后将导致整个问题不再稀疏(破坏了路标部分的对角块结构)。
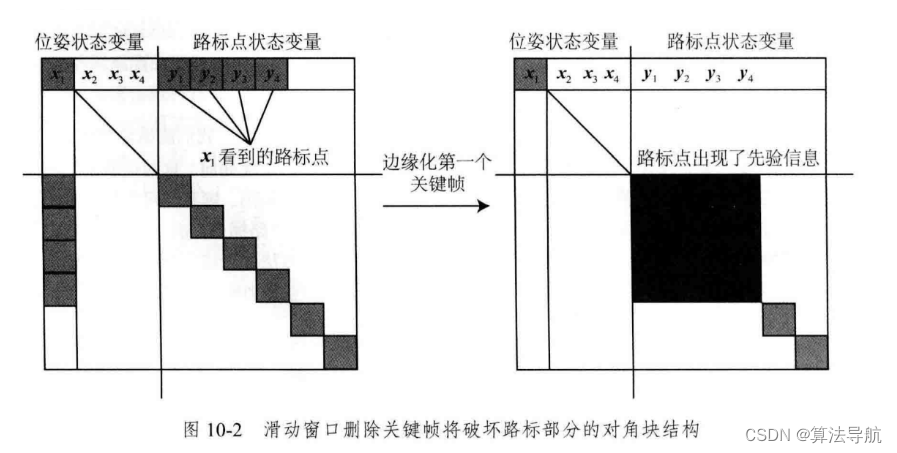
(3)滑动窗口法适合 VO 系统,而不适合大规模建图的系统。
9.2 位姿图
9.2.1 位姿图的意义
(1)随着时间的流逝,机器人的运动轨迹会越来越长,地图规模也会越来越大,BA 的计算效率就会下降。同时我们发现,经过若干次迭代后,收敛的特征点位置变化很小,发散的外点则已被剔除,因此在后续优化中没有必要再将收敛点考虑进来,而是只把他们当做位姿估计的约束。
(2)放开思路,我们完全可以构建一个只有轨迹的图优化,而位姿节点的边,可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。一旦初始估计完成,就不再优化那些路标点的位置,而只关心相机位姿之间的联系。这样的方式,省去了大量特征点优化的计算,只保留了关键帧的轨迹,构建了所谓的 位姿图。
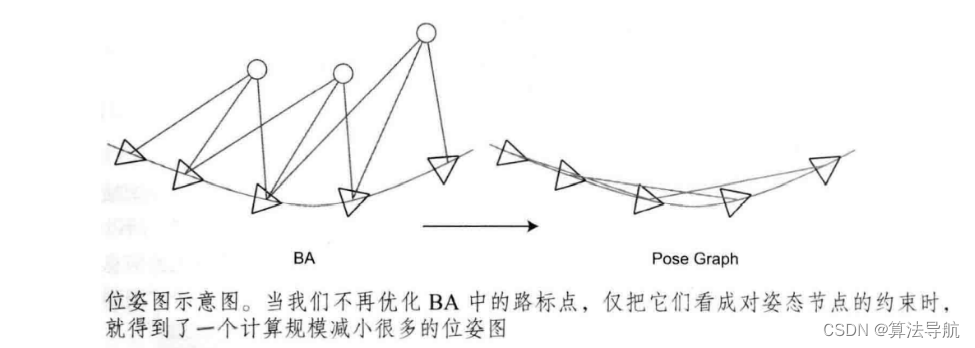
通过舍弃对路标点的优化,提高计算效率。
9.2.2 位姿图优化
位姿图中的节点表示相机位姿,用 T 1 , T 2 , . . . , T n , \boldsymbol{T}_1,\boldsymbol{T}_2,...,\boldsymbol{T}_n, T1,T2,...,Tn, 表示,边则是两个位姿节点之间相对运动的估计,这个估计可以通过特征点法或直接法得到。假设我们估计了 T i \boldsymbol{T}_i Ti 和 T j \boldsymbol{T}_j Tj 之间的相对运动 T i j \boldsymbol{T}_{ij} Tij,则有
T i T i j = T j \boldsymbol{T}_i \boldsymbol{T}_{ij}=\boldsymbol{T}_j TiTij=Tj
也即
T i j = T i − 1 T j (9-2) \boldsymbol{T}_{ij}=\boldsymbol{T}_i^{-1}\boldsymbol{T}_j \tag{9-2} Tij=Ti−1Tj(9-2)
写成李代数形式
ξ i j = ξ i − 1 ∘ ξ j = ln ( T i − 1 T j ) ∨ (9-3) \boldsymbol{\xi}_{i j}=\boldsymbol{\xi}_{i}^{-1} \circ \boldsymbol{\xi}_{j}=\ln \left(\boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\right)^{\vee} \tag{9-3} ξij=ξi−1∘ξj=ln(Ti−1Tj)∨(9-3)
将式(9-2)中的 Δ T i j \Delta \boldsymbol{T}_{ij} ΔTij 移至方程右侧,则
T i j − 1 T i − 1 T j = I (9-4) \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1}\boldsymbol{T}_j=\boldsymbol{I} \tag{9-4} Tij−1Ti−1Tj=I(9-4)
但实际上,并不可能完全相等。定义
e i j = ln ( T i j − 1 T i − 1 T j ) ∨ (9-5) \boldsymbol{e}_{ij}=\ln( \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1}\boldsymbol{T}_j)^{\vee} \tag{9-5} eij=ln(Tij−1Ti−1Tj)∨(9-5)
我们需要优化的是 T i \boldsymbol{T}_i Ti 和 T j \boldsymbol{T}_j Tj,也即 ξ i \boldsymbol{\xi}_i ξi 和 ξ j \boldsymbol{\xi}_j ξj,因此需要求这两个变量关于 e i j \boldsymbol{e}_{ij} eij 的导数。分别左乘一个左扰动: δ ξ i \boldsymbol{\delta \xi}_i δξi 和 δ ξ j \boldsymbol{\delta \xi}_j δξj
e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ exp ( ( δ ξ j ) ∧ T j ) ∨ (9-6) \boldsymbol{\hat{e}}_{ij}=\ln( \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1} \exp((-\boldsymbol{\delta \xi}_i)^{\wedge}\exp((\boldsymbol{\delta \xi}_j)^{\wedge} \boldsymbol{T}_j)^{\vee} \tag{9-6} e^ij=ln(Tij−1Ti−1exp((−δξi)∧exp((δξj)∧Tj)∨(9-6)
根据伴随矩阵的性质:
exp ( ( Ad ( T ) ξ ) ∧ ) = T exp ( ξ ∧ ) T − 1 (9-7) \exp \left((\operatorname{Ad}(\boldsymbol{T}) \boldsymbol{\xi})^{\wedge}\right)=\boldsymbol{T} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{T}^{-1} \tag{9-7} exp((Ad(T)ξ)∧)=Texp(ξ∧)T−1(9-7)
稍作改变(把 Ad ( T ) \operatorname{Ad}(\boldsymbol{T}) Ad(T) 移到右侧,$ \boldsymbol{T}^{-1}$ 移到左侧)
exp ( ξ ∧ ) T = T exp ( ( Ad ( T − 1 ) ξ ) ∧ ) (9-9) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{T}=\boldsymbol{T} \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}^{-1}\right) \boldsymbol{\xi}\right)^{\wedge}\right) \tag{9-9} exp(ξ∧)T=Texp((Ad(T−1)ξ)∧)(9-9)
那么,式(9-6)可写为(从右往左化简)
e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) exp ( δ ξ j ∧ ) T j ‾ ) ∨ = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) T j ‾ exp ( ( Ad ( T j − 1 ) δ ξ j ) ∧ ) ) ∨ = ln ( T i j − 1 T i − 1 T j exp ( ( − Ad ( T j − 1 ) δ ξ i ) ∧ ) exp ( ( Ad ( T j − 1 ) δ ξ j ) ∧ ) ) ∨ ≈ ln ( T i j − 1 T i − 1 T j [ I − ( Ad ( T j − 1 ) δ ξ i ) ∧ + ( Ad ( T j − 1 ) δ ξ j ) ∧ ] ) ∨ ≈ e i j + ∂ e i j ∂ δ ξ i δ ξ i + ∂ e i j ∂ δ ξ j δ ξ j (9-10) \begin{aligned} \hat{\boldsymbol{e}}_{i j} &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \exp \left(\left(-\boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \underline{\exp \left(\delta \boldsymbol{\xi}_{j}^{\wedge}\right) \boldsymbol{T}_{j}}\right)^{\vee} \\ &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \underline{\exp \left(\left(-\boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \boldsymbol{T}_{j}} \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right)\right)^{\vee} \\ &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j} \exp \left(\left(-\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right)\right)^{\vee} \\ & \approx \ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\left[\boldsymbol{I}-\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}+\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right]\right)^{\vee} \\ & \approx \boldsymbol{e}_{i j}+\frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{i}} \boldsymbol{\delta} \boldsymbol{\xi}_{i}+\frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{j}} \boldsymbol{\delta} \boldsymbol{\xi}_{j} \end{aligned} \tag{9-10} e^ij=ln(Tij−1Ti−1exp((−δξi)∧)exp(δξj∧)Tj)∨=ln(Tij−1Ti−1exp((−δξi)∧)Tjexp((Ad(Tj−1)δξj)∧))∨=ln(Tij−1Ti−1Tjexp((−Ad(Tj−1)δξi)∧)exp((Ad(Tj−1)δξj)∧))∨≈ln(Tij−1Ti−1Tj[I−(Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧])∨≈eij+∂δξi∂eijδξi+∂δξj∂eijδξj(9-10)
其中,第四步将两个指数一阶泰勒展开,相乘后舍去二次项;第四步到第五步则使用了 BCH 近似。
按照李代数上的求导法则,我们得到了误差关于两个位姿的雅克比矩阵,即
∂ e i j ∂ δ ξ i = − J r − 1 ( e i j ) Ad ( T j − 1 ) \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{i}}=-\mathcal{J}_{r}^{-1}\left(\boldsymbol{e}_{i j}\right) \operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) ∂δξi∂eij=−Jr−1(eij)Ad(Tj−1)
∂ e i j ∂ δ ξ j = J r − 1 ( e i j ) Ad ( T j − 1 ) (9-11) \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{j}}=\mathcal{J}_{r}^{-1}\left(\boldsymbol{e}_{i j}\right) \operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \tag{9-11} ∂δξj∂eij=Jr−1(eij)Ad(Tj−1)(9-11)
J r \mathcal{J}_{r} Jr 的形式比较复杂,通常取它的近似,
J r − 1 ( e i j ) ≈ I + 1 2 [ ϕ e ∧ ρ e ∧ 0 ϕ e ∧ ] (9-12) \mathcal{J}_{r}^{-1}\left(e_{i j}\right) \approx \boldsymbol{I}+\frac{1}{2}\left[\begin{array}{cc} \phi_{e}^{\wedge} & \rho_{e}^{\wedge} \\ 0 & \phi_{e}^{\wedge} \end{array}\right] \tag{9-12} Jr−1(eij)≈I+21[ϕe∧0ρe∧ϕe∧](9-12)
了解雅克比求导后,剩下的部分就是普通的图优化。 记所有的边(也就是位姿)为 E \mathcal{E} E,则总体目标函数为
min 1 2 ∑ i , j ∈ E e i j T Σ i j − 1 e i j (9-13) \min \frac{1}{2} \sum_{i, j \in \mathcal{E}} \boldsymbol{e}_{i j}^{\mathrm{T}} \boldsymbol{\Sigma}_{i j}^{-1} \boldsymbol{e}_{i j} \tag{9-13} min21i,j∈E∑eijTΣij−1eij(9-13)
然后再用高斯牛顿法或 L-M 法优化求解。
相关文章:

《视觉SLAM十四讲》-- 后端 2
文章目录 09 后端 29.1 滑动窗口滤波和优化9.1.1 实际环境下的 BA 结构9.1.2 滑动窗口法 9.2 位姿图9.2.1 位姿图的意义9.2.2 位姿图优化 09 后端 2 9.1 滑动窗口滤波和优化 9.1.1 实际环境下的 BA 结构 由于计算机算力的限制,我们必须控制 BA 的规模,…...
安装插件时Vscode XHR Failed 报错ERR_CERT_AUTHORITY_INVALID
安装插件时Vscode XHR Failed 报错ERR_CERT_AUTHORITY_INVALID 今天用vscode 安装python插件时报XHR failed,无法拉取应用商城的数据, 报的错如下: ERR_CERT_AUTHORITY_INVALID 翻译过来就是证书有问题 找错误代码的方法: 打开vscode, 按F1…...
)
ON_WM_TIMER()
ON_WM_TIMER() static_cast: cannot convert from void (__cdecl CPop::* )(UINT) to void (__cdecl CWnd::* )(UINT_PTR) OnTimer(UINT nIDEvent) ----> OnTimer(UINT_PTR nIDEvent)...
【Unity】单例模式及游戏声音管理类应用
【Unity】单例模式及游戏声音管理类应用 描述 在日常游戏项目开发中,单例模式是一种常用的设计模式,它允许在应用程序的生命周期中只创建一个对象实例,并提供对该实例的全局访问点。通过使用单例模式,可以提高代码的可维护性和可…...

视频剪辑技巧:轻松搞定视频随机合并,一篇文章告知所有秘诀
在视频制作的过程中,视频随机合并是一种创新的剪辑手法,它打破了传统的线性剪辑模式,使得视频剪辑更加灵活和有趣。通过将不同的视频片段随机组合在一起,我们可以创造出独特的视觉效果和情感氛围。这种剪辑方式让观众在观看视频时…...

torch.stack
看网上看多没讲的不是很明白,我来试试空间上的理解 # 假设是时间步T1的输出 T1 torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]]) # 假设是时间步T2的输出 T2 torch.tensor([[10, 20, 30],[40, 50, 60],[70, 80, 90]])输出: print(torch.stack((T1,T2…...

手搓哈希表、列表、队列,只为了用C语言快速求解华容道游戏,我不是大佬,只是一个游戏算法爱好者
背景 多年前曾经写过C语言求解华容道,当时没有用到哈希表,导致整个查重搜索数组过大,每次求解都得花上数分钟的时间,如今时过境迁,对数据结构和算法有了更深的理解,所以得把这一块补上了。(其实就是最近想…...

MySQL 的执行原理(一)
5.1 单表访问之索引合并 我们前边说过 MySQL 在一般情况下执行一个查询时最多只会用到单个二级 索引,但存在有特殊情况,在这些特殊情况下也可能在一个查询中使用到多个二 级索引,MySQL 中这种使用到多个索引来完成一次查询的执行方法称之为&…...
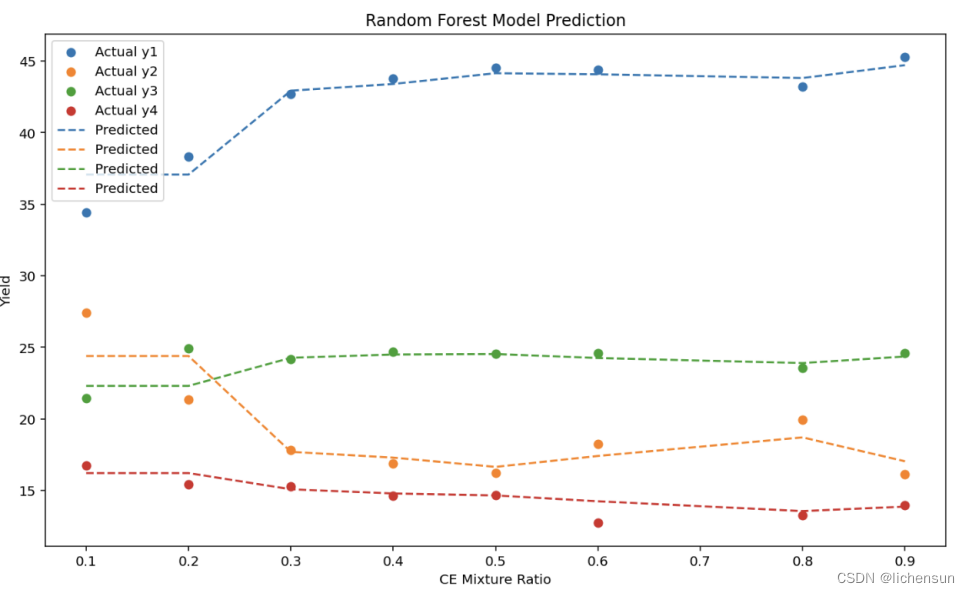
2023_“数维杯”问题B:棉秸秆热解的催化反应-详细解析含代码
题目翻译: 随着全球对可再生能源需求的不断增加,生物质能作为一种成熟的可再生能源得到了广泛的关注。棉花秸秆作为一种农业废弃物,因其丰富的纤维素、木质素等生物质成分而被视为重要的生物质资源。虽然棉花秸秆的热解可以产生各种形式的可…...

django理解01
接在Vue理解01后 项目创建 pycharm上下载django框架 在需要创建项目的文件夹终端django-admin startproject 项目名终端创建APPpython manage.py startapp app名注册APP,settings.py里INSTALLED_APPS下,增加一项:app名.apps.类名࿰…...
限制Domain Admin登录非域控服务器和用户计算机
限制Domain Admin管理员使用敏感管理员帐户(域或林中管理员组、域管理员组和企业管理员组中的成员帐户)登录到信任度较低的服务器和用户端计算机。 此限制可防止管理员通过登录到信任度较低的计算机来无意中增加凭据被盗的风险。 建议采用的策略 建议使用以下策略限制对信任度…...
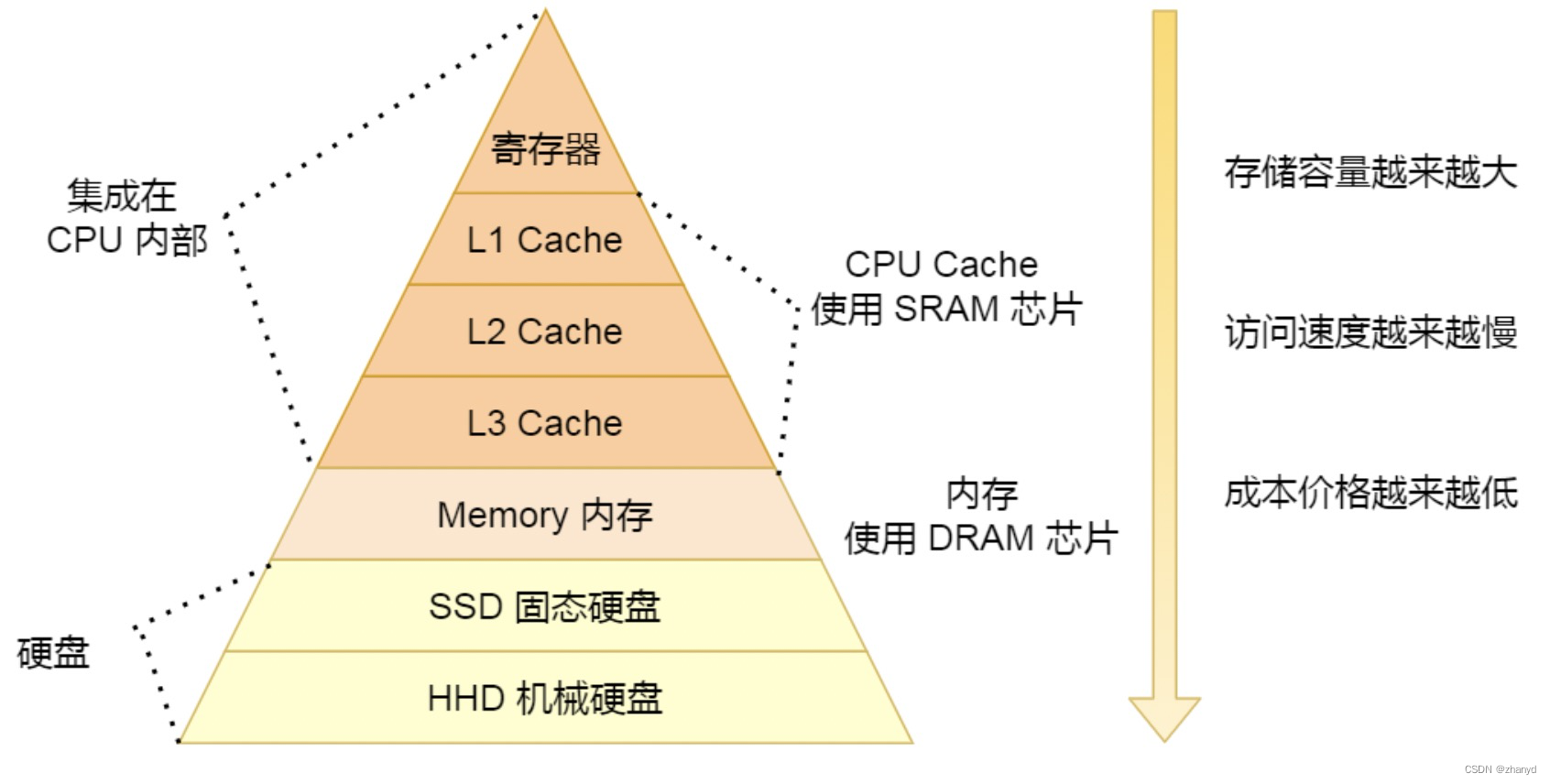
原来机械硬盘比内存慢10万倍
我们都知道机械硬盘的速度很慢,内存的速度很快,那么不同存储器之间的差距到底有多大呢? 我们先来看一幅图: CPU访问寄存器的时间是0.3纳秒,访问L1高速缓存的时间是1纳秒,访问L2高速缓存的时间是4纳秒… 秒…...

ElementUI的Dialog弹窗实现拖拽移动功能
文章目录 1. ElementUI简介2. 弹窗基本使用3. 实现拖拽移动功能4. 拓展与分析 🎉欢迎来到Java学习路线专栏~ElementUI的Dialog弹窗实现拖拽移动功能 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客🎈该系列文章专栏&a…...
生成式AI模型量化简明教程
在不断发展的人工智能领域,生成式AI无疑已成为创新的基石。 这些先进的模型,无论是用于创作艺术、生成文本还是增强医学成像,都以产生非常逼真和创造性的输出而闻名。 然而,生成式AI的力量是有代价的—模型大小和计算要求。 随着生…...

机器人制作开源方案 | 智能快递付件机器人
一、作品简介 作者:贺沅、聂开发、王兴文、石宇航、盛余庆 单位:黑龙江科技大学 指导老师:邵文冕、苑鹏涛 1. 项目背景 受新冠疫情的影响,大学校园内都采取封闭式管理来降低传染的风险,导致学生不能外出,…...
PostgreSQL技术大讲堂 - 第34讲:调优工具pgBagder部署
PostgreSQL从小白到专家,是从入门逐渐能力提升的一个系列教程,内容包括对PG基础的认知、包括安装使用、包括角色权限、包括维护管理、、等内容,希望对热爱PG、学习PG的同学们有帮助,欢迎持续关注CUUG PG技术大讲堂。 第34讲&#…...

《Python日志新宠——Loguru,轻松记录,笑对Bug!》
嘿,程序媛和程序猿们!👩💻👨💻 你们是不是也曾为日志处理这个“小事”而头疼?别着急,今天我给你们介绍一个简直比拥抱泰迪熊还要温暖的Python库——Loguru!这货不仅强…...

NET8 ORM 使用AOT SqlSugar
.NET AOT8 基本上能够免强使用了, SqlSugar ORM也支持了CRUD 能在AOT下运行了 Nuget安装 SqlSugarCore 具体代码 StaticConfig.EnableAot true;//启用AOT 程序启动执行一次就好了//用SqlSugarClient每次都new,不要用单例模式 var db new SqlSugarClient(new ConnectionC…...

CCRC认证是什么?
什么是CCRC认证? 信息安全服务资质,是信息安全服务机构提供安全服务的一种资格,包括法律地位、资源状况、管理水平、技术能力等方面的要求。 信息安全服务资质(CCRC)是依据国家法律法规、国家标准、行业标准和技术规范…...
)
linux内核面试题(2)
整理了一些网上的linux驱动岗位相关面试题,如果错误,欢迎指正。 工作队列是运行在进程上下文,还是中断上下文?它的回调函数是否允许睡眠? 工作队列是运行在进程上下文的。工作队列的回调函数是允许睡眠的,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
