【学习笔记】NOIP爆零赛8
trash ,但不完全是trash
t1t1t1考了一个神奇的结论还没有证明,t2t2t2玩了一些复杂度的花样,t3t3t3稍微阳间一点,是一个并不复杂的容斥,如果放在t1t1t1可能更合适一些,t4t4t4就是在原题的基础上改了一下然后就成了一道毒瘤数据结构题,
t1t1t1总之感觉还是出的很烂,所以就不管它了
t2t2t2暴力能过,很显然留在最后补
t3t3t3赛时过了,那没什么了
所以只要胡一下t4t4t4就好是吗
补数据结构题是最痛苦的
最小生成树
首先有一道原题:[HNOI2010]城市建设 ,于是你不需要用这道题的任何性质就可以得到80pts80pts80pts。
这就是场上的最优解了,毕竟正解的思路非常人能及,而且也就少了20pts20pts20pts而已,不过唯一的缺点是码量有点大
不过正解的话从链入手似乎非常合理,但是只有40pts40pts40pts,最后的数据结构维护还是非常难想,所以这道题的性价比真的不高啊
对于链的情况,可以看成是[1,n][1,n][1,n]的若干不相交区间[li,ri][l_i,r_i][li,ri]通过与000节点连边从而联通,因此在用线段树维护区间信息时,只用处理中间两个连通块。如果都不与000联通,那么不合法;如果都与000联通,不需要花费代价就可以合并,如果只有一边与000联通,那么需要花费中间那条二类边的代价。结合画图不难理解。
搞清楚链的情况后,我们就有了40pts40pts40pts 好少啊,考场上思考数据结构完全没有动力啊
推广到一般情况,我们只需要一步:求出一棵树对应的等效链 。这看起来非常不可思议,但是如果你把两棵树合并看成两条链合并,然后套用链的维护方式就不难理解了。
这个地方很容易给人一个误解,就是直接将结论扩展好像可以一步到位。
事实上,我们还需要下一个结论:假设当前加的边是u,vu,vu,v,其分属于连通块SSS,TTT,那么我们可以把u,vu,vu,v这条边等效成任意u′∈S,v′∈Tu'\in S,v'\in Tu′∈S,v′∈T之间的连边,当然边权不变。其原因在于,如果u,vu,vu,v这条边在MSTMSTMST中,那么此时S,TS,TS,T一定是联通的(假设不是联通的,那么跑kruskal\text{kruskal}kruskal算法的流程就会出现矛盾)。因此,我们可以把一棵树 彻底等效成一条链 。
基于上述观察,我们不难得到将所有的二类边构成的森林等价转化成若干条链,然后用线段树维护答案的做法。
复杂度O(nlogn)O(n\log n)O(nlogn)。考场上能想到标算还是挺nbnbnb的
最后还是补一下t2t2t2。代码就算了,能过的代码为什么要优化呀
二进制的世界
用暴力来优化暴力
正解不如暴力
将161616位分为两部分:前888位和后888位。相信大家都猜到复杂度了吧,不过用乱搞优化位运算的确令人烦躁
设fi,jf_{i,j}fi,j表示前888位为iii的数,与某个后888为是jjj的数进行位运算,后888位结果的最大值以及方案数。
那么加入一个数xxx的时候,设它的前888位为aaa,后八位为bbb,只需要枚举jjj,用joptbj\ opt\ bj opt b更新所有fa,jf_{a,j}fa,j。查询xxx的时候,用所有(iopta)<<8∣fi,b(i\ opt\ a)<<8|f_{i,b}(i opt a)<<8∣fi,b更新答案。
复杂度O(nm)O(n\sqrt{m})O(nm)。
代码出奇好写
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
using namespace std;
const int N=1e5+5;
int n,type,a[N],f[1<<8][1<<8],g[1<<8][1<<8];
string op;
int calc(int x,int y){if(op[0]=='x')return x^y;else if(op[0]=='o')return x|y;return x&y;
}
void ins(int x){int a=x>>8,b=x^(a<<8);for(int i=0;i<1<<8;i++){if(calc(b,i)>f[a][i]){f[a][i]=calc(b,i);g[a][i]=1;}else if(calc(b,i)==f[a][i]){g[a][i]++;}}
}
pair<int,int>solve(int x){int a=x>>8,b=x^(a<<8),res=0,res2=0;for(int i=0;i<1<<8;i++){if(g[i][b]&&((calc(a,i)<<8)|f[i][b])>res){res=((calc(a,i)<<8)|f[i][b]);}} for(int i=0;i<1<<8;i++){if(g[i][b]&&((calc(a,i)<<8)|f[i][b])==res){res2+=g[i][b];}}return {res,res2};
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>op>>type;for(int i=1;i<=n;i++)cin>>a[i];ins(a[1]);for(int i=2;i<=n;i++){pair<int,int>res=solve(a[i]);if(!type){cout<<res.fi<<"\n";}else {cout<<res.fi<<" "<<res.se<<"\n";}ins(a[i]);}
}
相关文章:

【学习笔记】NOIP爆零赛8
trash ,但不完全是trash t1t1t1考了一个神奇的结论还没有证明,t2t2t2玩了一些复杂度的花样,t3t3t3稍微阳间一点,是一个并不复杂的容斥,如果放在t1t1t1可能更合适一些,t4t4t4就是在原题的基础上改了一下然后就成了一道毒…...
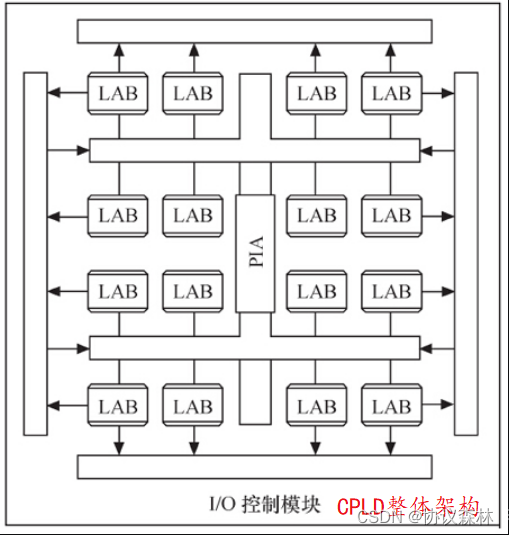
【Linux驱动】驱动设计硬件基础----串口、I2C、SPI、以太网接口、PCIE
1.前言 常见的外设接口与总线的工作方式,包括串口、I2C、SPI、USB、以太网接口、PCI和PCI-E、SD和SDIO等。 2.串口 RS-232、RS-422与RS-485都是串行数据接口标准,最初都是由电子工业协会(EIA)制订并发布的。 3.I2C I2C&…...

同为(TOWE)防雷产品助力福建移动南平分公司防雷改造
01 公司简介中国移动通信集团福建有限公司南平分公司属于福建移动地级分公司,所属行业为电信、广播电视和卫星传输服务。现已建成覆盖范围广、业务品种多、通信质量高的综合通信网络,具备行业领先的经营管理制度。移动通信大楼的综合防雷及地接系统&…...

Win10安装mediapipe的步骤
我之前想自己安装mediapipe包进行人体检测的学习,但整了好几个月都不行,这次终于让我整好了,我的python版本为python 3.7.1。注意,不要直接用pip install mediapipe 进行安装,我之前这样安装的,mediapipe安…...
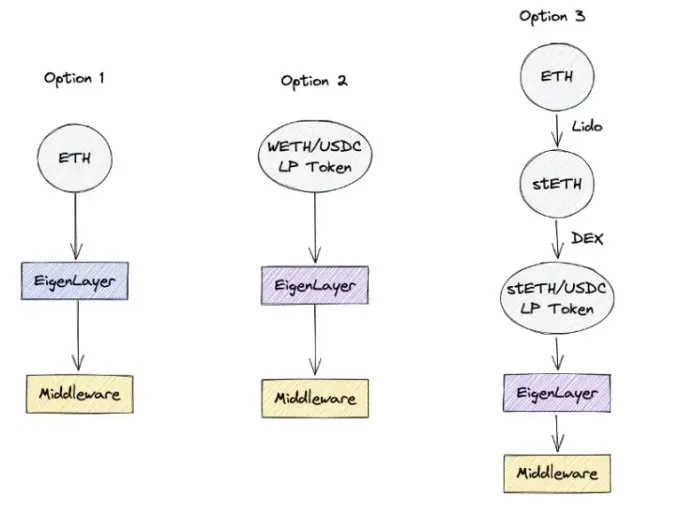
项目调研丨以太坊再质押项目EigenLayer白皮书四大看点(内附完整版中文白皮书)
北京时间2月21日下午,被众多一线投研机构视为2023年以太坊最重要的创新,有可能开启以太坊新叙事方向的项目Eigenlayer终于披露了其第一版白皮书。EigenLayer是以太坊的再质押集,允许共识层ETH质押者选择验证构建在以太坊生态系统之上的新软件…...
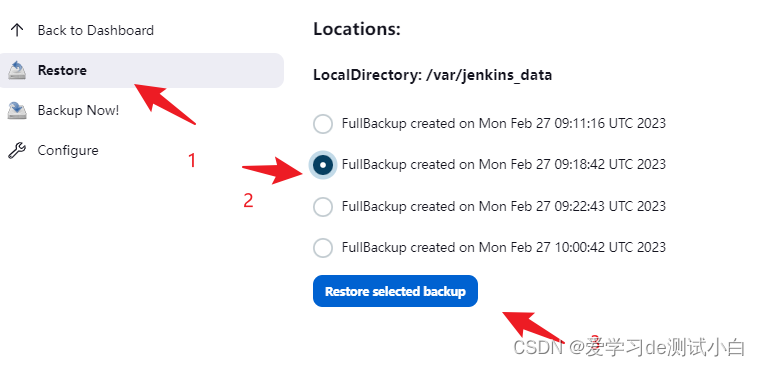
51-Jenkins-Periodic Backup插件实现Jenkins备份
Periodic Backup插件实现Jenkins备份前言目录结构插件备份安装插件使用插件前言 本篇来学习下使用Periodic Backup插件实现Jenkins备份 目录结构 Jenkins的所有数据都是存放在文件中的,所以,Jenins备份其实就是备份Jenkins_HOME目录。 Jenkins_Home目…...
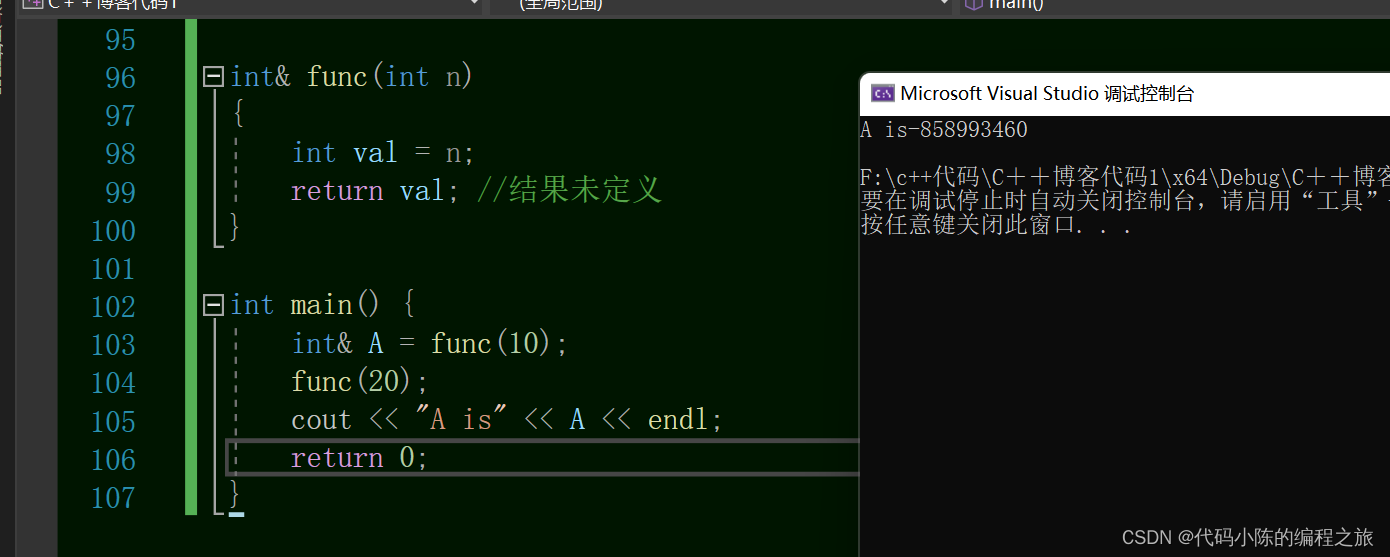
C++之入门之引用,内联函数
一、引用 1、引用的概念 在C中,引用的本质其实就是给一个已经存在的变量”起别名“。也就是说,引用与它所引用的对象共用一块空间。(同一块空间的多个名字) 就比如说,李逵又叫黑旋风,而黑旋风就是指李逵…...

linux kprobe使用
使用场景 监控某个内核函数是否被调用获取某个内核函数耗费的时间获取某个内核函数的入参获取某个内核函数的调用栈(dump_stack())获取某个内核函数的返回值 参数传递规则 x86平台对pt_regs的定义 arch/x86/include/asm/ptrace.h // i386架构 #ifdef…...
)
2023年超全前端面试题-背完稳稳拿offer(欢迎补充)
HTML、CSS相关 HTML5 HTML5新特性 增强了表单,input新增了一些type: color----定义调色板 tel-----定义包含电话号码的输入域 email—定义包含email地址的输入域 search–定义搜索域 number–定义包含数值的输入域 date----定义选取日、月、年的输入域…...

python之web自动化测试框架
梳理下搭建web自动化框架的流程: 创建目录: cases:存放测试用例,unittest框架要求用例名必须以test开头,所以命名test_case.py test_case.py代码如下:继承unittest.TestCase类下面的方法setupclass(),te…...
算法笔记(十五)—— 动态规划(暴力递归到动态规划)习题训练!
通过递归到记忆化搜索再到严格表结构的动态规划 递归方法的评价:1. 单可变参数的维度;2. 可变参数的个数 记忆化搜索 在暴力递归中会存在很多的重复计算,可以使用存储结构来实现空间换时间。 严格表结构的动态规划 整理位置之间的依赖关系…...
云原生架构基础概念及应用办法
什么是云原生? 云原生是一种基于容器、微服务和自动化运维的软件开发和部署方法。它可以使应用程序更加高效、可靠和可扩展,适用于各种不同的云平台。 如果要更直接通俗的来解释下上面的概念。 云原生更准确来说就是一种文化,是一种潮流&a…...
RedisTemplate 的基本使用手把手教
下载实例源码 使用步骤 1、引入 spring-boot-starter-data-redis 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency>2、在 application.yml 配置 R…...

Hbase -- Compact工具梳理
1. 背景 当前,线上HBase集群的自动Major Compact是关闭的,我们选择在凌晨业务空闲的时候进行手动触发Major Compact,Compact工具就是在运维平台上对资源组、RS、表进行Major Compact。目前线上有2种版本的Compact程序:Compact_v1…...

【java代码审计】SQL注入
1 原理 没有正确的对用户的输入进行检查,将用户的输入以拼接的方式带入到SQL语句中,导致SQL注入。 2 产生SQL注入的原因 2.1 JDBC拼接不当造成SQL注入 前置知识: JDBC执行SQL语句的两种方式: PrepareStatement:会对…...

前置知识-辛 Runge-Kutta 方法
1.3.3 辛 Runge-Kutta 方法 将方程 ( 1.10.2 ) (1.10 .2) (1.10.2) 改写为 d z d x =...

require 与 import 两种引入模块方式到底有什么区别?
关于JavaScript 的模块化规范,可以移步至: 【JavaScript高级】模块化规范「一文让你彻底搞懂前端模块化规范 & 区别」 下面进入正题 require 与 import 两种引入模块方式,到底有什么区别呢? 大致可以分为以下几个方面&#…...
软考信息系统监理师备考建议
用好备考方法,两三个月就可以过的。信息系统监理师备考最好以教材和历年真题为主,教学视频模拟题为辅。考试介绍与复习建议:考试设置的科目包括:(1)信息系统工程监理基础知识,考试时间150分钟&a…...
第八届蓝桥杯省赛——4承压计算(二维数组,嵌套循环)
题目:X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。每块金属原料的外形、尺寸完全一致,但重量不同。金属材料被严格地堆放成金字塔形。7 5 8 7 8 8 9 2 7 2 8 1 4 9 1 8 1 8 8 4 1 7 9 6 1 4 5 4 5 6 5 5 6 9 5 6 5 5 4 7 9 3 5 5 1 7 5 7 9 7 4…...
)
【ECNU】3645. 莫干山奇遇(C++)
目录 题目 输入格式 输出格式 样例 提示 思路 代码 题目 单点时限: 2.0 sec 内存限制: 512 MB 出题人当然是希望出的题目有关 oxx,于是想方设法给题目配上一些有关 oxx 的背景故事,使得它看起来不那么无趣。但有的时候却无法引入合适的小姐姐&…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
