C++二分查找算法:查找和最小的 K 对数字
相关专题
二分查找相关题目
题目
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。
示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数:
[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
示例 3:
输入: nums1 = [1,2], nums2 = [3], k = 3
输出: [1,3],[2,3]
解释: 也可能序列中所有的数对都被返回:[1,3],[2,3]
参数范围:
1 <= nums1.length, nums2.length <= 105
-109 <= nums1[i], nums2[i] <= 109
nums1 和 nums2 均为升序排列
1 <= k <= 104
分析
本题还可以用多路归并。
时间复杂度
O(log(m)*o(n2))+O(k+n1)。m是nums1和nums2的最大值。n1是nums1的长度,n2是nums2的长度。
步骤
一,二分找到和第k小的数对的和right。
二,收集所有和小于right的数对,和等于right的数对只收集llEqualNum 对,GetLessEqualNum(nums1, nums2, right - 1)是少于right的数对数量。
GetLessEqualNum
此函数的作用:求和小于等于iSum数对数量。
std::upper_bound(nums2.begin(), nums2.end(), iSum - n)- nums2.begin(); 是数对(n,?) 之和小于等于iSum的数量。
注意: 返回值可能是1e10,超过int的返回,所以返回值用long long。
和第k小的数对的和
第一个符合以下的要求的iSum(符合要求的最小iSum) ,和小于等于iSum的数对数量大于等于k。
代码
核心代码
class Solution {
public:vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {int left = nums1[0] + nums2[0] - 1, right = nums1.back() + nums2.back();while (right - left > 1){const auto mid = left + (right - left) / 2;if (GetLessEqualNum(nums1, nums2, mid) >= k){right = mid;}else{left = mid;}}long long llEqualNum = k - GetLessEqualNum(nums1, nums2, right - 1);vector<vector<int>> vRet;for (const auto& n : nums1){for (const auto n2 : nums2){if (n + n2 < right){vRet.emplace_back(vector<int>{n, n2});}else if ((n + n2 == right)&&(llEqualNum)){llEqualNum--;vRet.emplace_back(vector<int>{n, n2});}else{break;}}}return vRet;}long long GetLessEqualNum(const vector<int>& nums1, const vector<int>& nums2, int iSum){long long llNum = 0;for (const auto& n : nums1){llNum += std::upper_bound(nums2.begin(), nums2.end(), iSum - n)- nums2.begin();}return llNum;}
};
测试代码
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}
int main()
{
vector nums1, nums2;
int k;
vector<vector> res;
{
Solution slu;
nums1 = { -10,-4,0,0,6 }, nums2 = { 3,5,6,7,8,100 };
k = 10;
res = slu.kSmallestPairs(nums1, nums2, k);
Assert(vector<vector>{ { {-10, 3}, { -10,5 }, { -10,6 }, { -10,7 }, { -10,8 }, { -4,3 }, { -4,5 }, { -4,6 }, { 0,3 }, { 0,3 }}}, res);
}
{
Solution slu;
nums1 = { 1,7,11 }, nums2 = { 2,4,6 };
k = 3;
res = slu.kSmallestPairs(nums1,nums2, k);
Assert(vector<vector>{ {1, 2}, { 1,4 }, { 1,6 }}, res);
}
{
Solution slu;
nums1 = { 1,1,2 }, nums2 = { 1,2,3 };
k = 2;
res = slu.kSmallestPairs(nums1, nums2, k);
Assert(vector<vector>{ {1, 1}, { 1,1 }}, res);
}
{
Solution slu;
nums1 = { 1,2 }, nums2 = { 3 };
k = 3;
res = slu.kSmallestPairs(nums1, nums2, k);
Assert(vector<vector>{ {1, 3}, { 2,3 }}, res);
}
//CConsole::Out(res);
}
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 洒家想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

C++二分查找算法:查找和最小的 K 对数字
相关专题 二分查找相关题目 题目 给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。 定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。 请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。 示例 1:…...
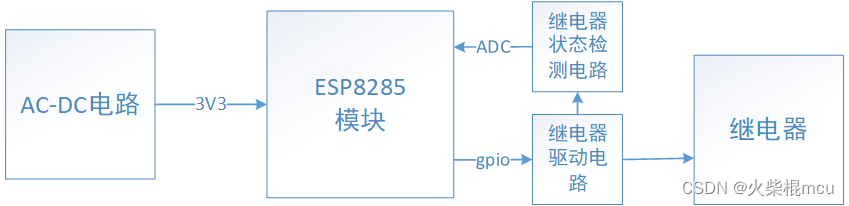
开源WIFI继电器之方案介绍
一、实物 1、外观 2、电路板 二、功能说明 输出一路继电器常开信号,最大负载电流10A输入一路开关量检测联网方式2.4G Wi-Fi通信协议MQTT配网方式AIrkiss,SmartConfig设备管理本地Web后台管理,可配置MQTT参数供电AC220V其它一个功能按键&…...
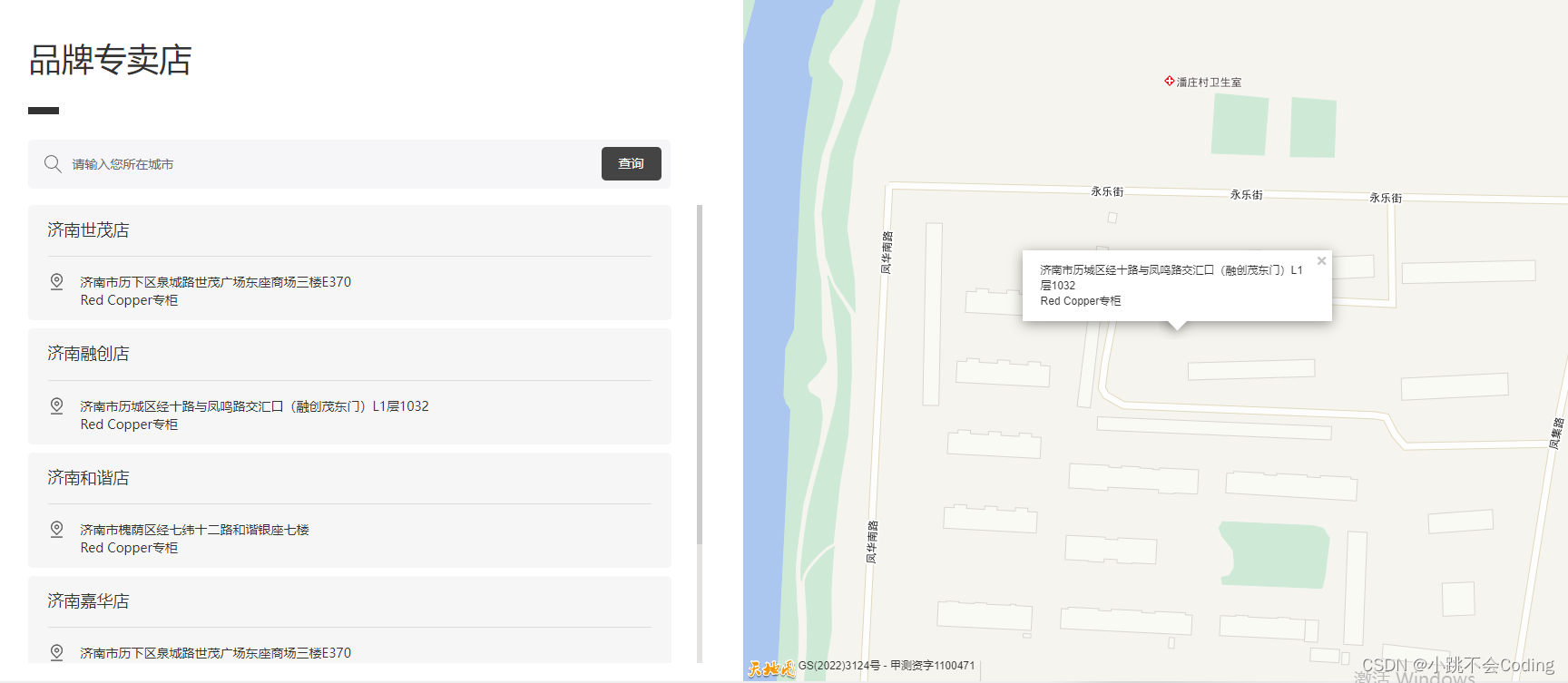
html使用天地图写一个地图列表
一、效果图: 点击左侧地址列表,右侧地图跟着改变。 二、代码实现: 一进入页面时,通过body调用onLoad"onLoad()"函数,确保地图正常显示。 <body onLoad"onLoad()"><!--左侧代码-->…...

C++ Qt 学习(九):模型视图代理
1. Qt 模型视图代理 Qt 模型视图代理,也可以称为 MVD 模式 模型(model)、视图(view)、代理(delegate)主要用来显示编辑数据 1.1 模型 模型 (Model) 是视图与原始数据之间的接口 原始数据可以是:数据库的一个数据表、内存中的一个 StringListÿ…...
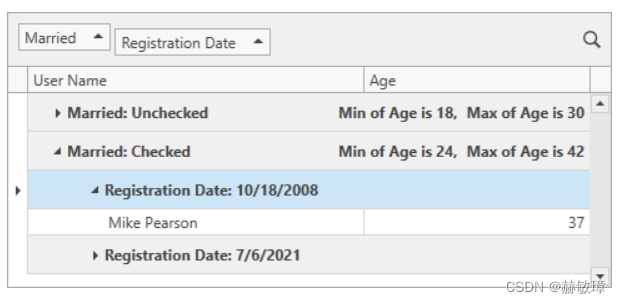
wpf devexpress 自定义统计
总计统计和分组统计包含预定义总计函数。这些函数允许你计算如下: 数据列的数量(Count) 最大和最小值(Max和Min) 总计和平均值(Sum和Average) 处理GridControl.CustomSummary 事件或者使用 GridControl.CustomSumm…...

【Flink】Flink任务缺失Jobmanager日志的问题排查
Flink任务缺失Jobmanager日志的问题排查 问题不是大问题,不是什么代码级别的高深问题,也没有影响任务运行,纯粹因为人员粗心导致,记录一下排查的过程。 问题描述 一个生产环境的奇怪问题,环境是flink1.15.0 on yarn…...

教程:使用 Keras 优化神经网络
一、介绍 在 我 之前的文章中,我讨论了使用 TensorFlow 实现神经网络。继续有关神经网络库的系列文章,我决定重点介绍 Keras——据说是迄今为止最好的深度学习库。 我 从事深度学习已经有一段时间了,据我所知,处理…...

什么是PWA(Progressive Web App)?它有哪些特点和优势?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

深入理解MongoDB的CRUD操作
MongoDB,一个广受欢迎的NoSQL数据库,以其灵活的文档模型、强大的查询能力和易于扩展的特性而著称。对于初学者和经验丰富的开发人员来说,熟练掌握MongoDB的增删改查(CRUD)操作是至关重要的。本博客将深入探讨如何在Mon…...
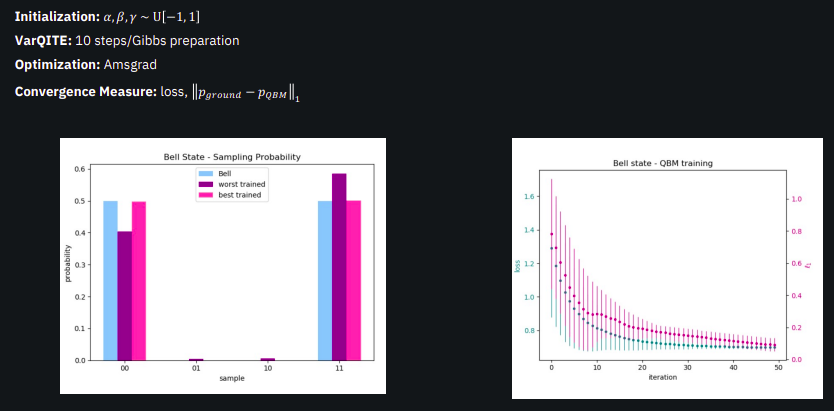
使用量子玻尔兹曼机推进机器学习:新范式
一、说明 量子玻尔兹曼机(QBM)是量子物理学和机器学习的前沿融合。通过利用叠加和纠缠等量子特性的力量,QBM 可以同时探索多个解决方案,使其异常擅长解决复杂问题。它使用量子位(量子计算的构建模块)以传统…...
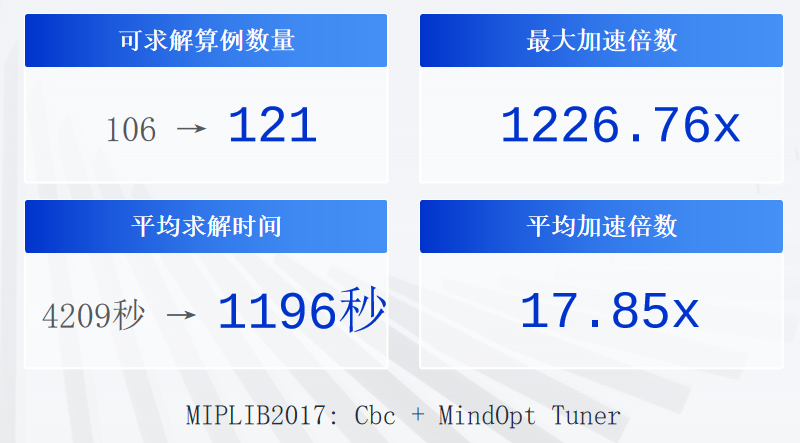
优化|优化求解器自动调参
原文信息:MindOpt Tuner: Boost the Performance of Numerical Software by Automatic Parameter Tuning 作者:王孟昌 (达摩院决策智能实验室MindOpt团队成员) 一个算法开发者,可能会幻想进入这样的境界:算…...
vite vue3配置eslint和prettier以及sass
准备 教程 安装eslint 官网 vue-eslint ts-eslint 安装eslint yarn add eslint -D生成配置文件 npx eslint --init安装其他插件 yarn add -D eslint-plugin-import eslint-plugin-vue eslint-plugin-node eslint-plugin-prettier eslint-config-prettier eslint-plugin…...

C语言第入门——第十六课
目录 一、分治策略与递归 二、递归 1.求解n的阶乘 2.输入整数、倒序输出 3.输入整数、正序输出 4.计算第n位Fibonacci数列 编辑5.无序整数数组打印 6.找到对应数组下标 一、分治策略与递归 在我们遇到大问题的时候,我们的正确做法是将它分解成小问题&a…...

IntelliJ IDEA 快捷键 Windows 版本
前言:常用快捷键 IntelliJ IDEA编辑器大受欢迎的原因之一是它的智能提示和丰富的快捷键,在日常开发中熟练的使用快捷键会大大提升开发的效率,本篇文章就笔者日常开发中的总结,把常用的、好用的快捷键做一个列表,方便…...

重生之我必去大厂java开发
JavaDreamer 重生之我必去大厂java开发。主线任务进入大厂java开发。 author :developer_zxh GitHub | Gitee 本项目记录了本人从中国科学院大学硕士研究生开始,如何进入大工 java 开发岗位的学习记录(目前在校未求职,加入后此状…...
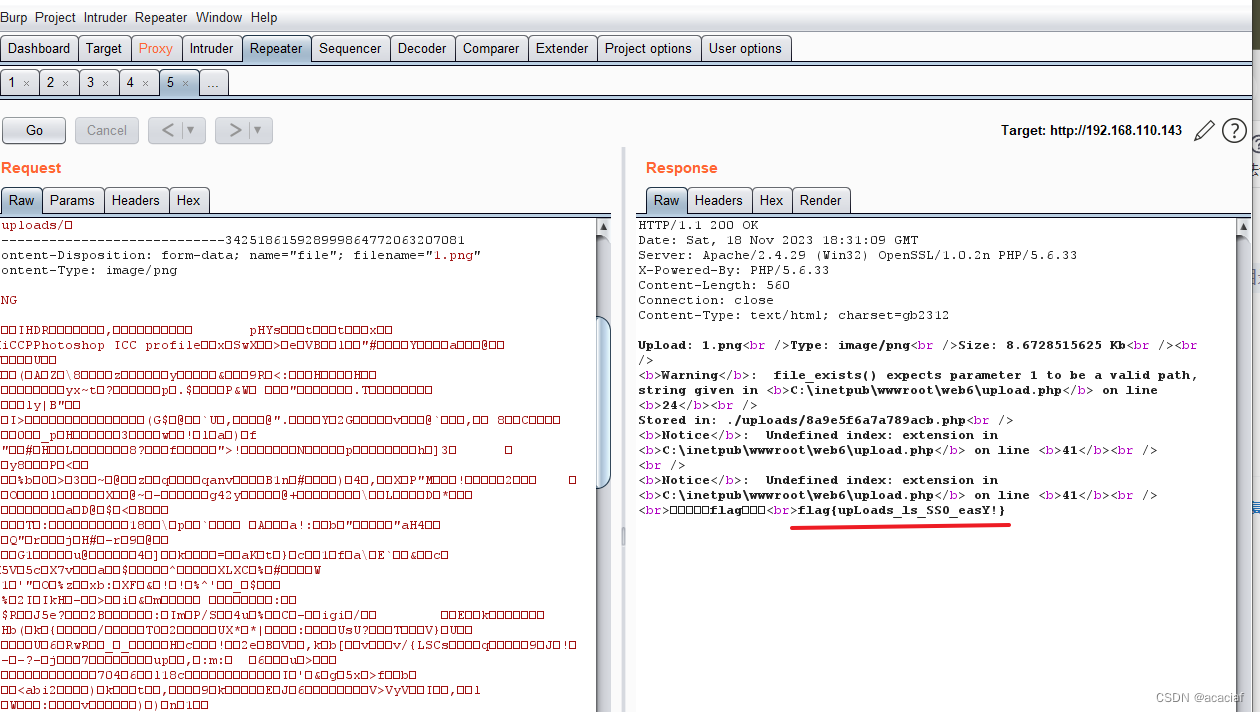
2023年中职“网络安全“—Web 渗透测试②
2023年中职“网络安全“—Web 渗透测试② Web 渗透测试任务环境说明:1.访问http://靶机IP/web1/,获取flag值,Flag格式为flag{xxx};2.访问http://靶机IP/web2/,获取flag值,Flag格式为flag{xxx};3.访问http://靶机IP/web…...
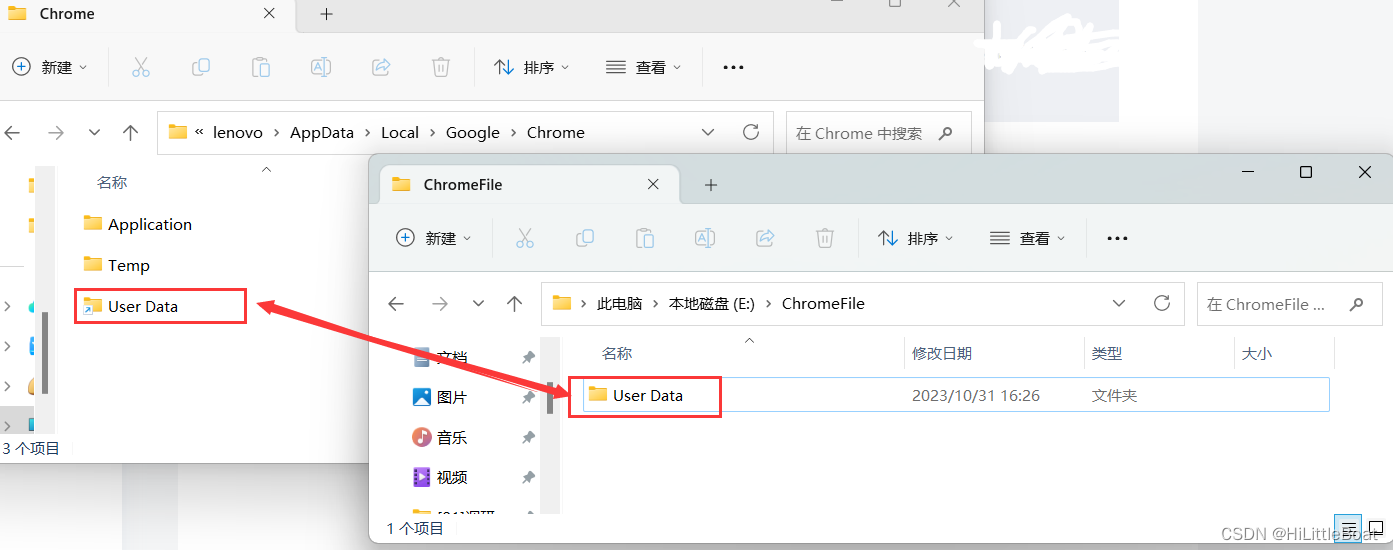
【整顿C盘】pycharm、chrome等软件,缓存移动
C盘爆了,特来找一下巨大的软件缓存,特此记录,跟随的各大教程,和自己的体会 一、爆炸家族JetBrains 这个适用于pycharm、idea、webstorm等等,只要是JetBrains家的,2020版本以上,都是一样的方法 p…...

C# using语句使用介绍
在C#中,using语句有两种主要用途:一是引入命名空间,二是提供一种简便的方式来处理资源的清理(主要用于实现了 IDisposable 接口的对象)。 引入命名空间:using 语句用于引入命名空间,从而可以在代…...
 201. 数字范围按位与 (位运算))
leetcode (力扣) 201. 数字范围按位与 (位运算)
文章目录 题目描述思路分析完整代码 题目描述 给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。 示例 1: 输入:left 5, right 7 输出…...
Flutter笔记: 在Flutter应用中使用SQLite数据库
Flutter笔记 在Flutter应用中使用SQLite数据库(基于sqflite) 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/q…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
