小美的树上染色
美团2024届秋招笔试第一场编程真题
 先提一个小知识:题目中凡是提到树结构都要使用图的存储方式,只有二叉树例外。
先提一个小知识:题目中凡是提到树结构都要使用图的存储方式,只有二叉树例外。
分析:在树结构中,孩子和父节点是相邻节点,而父节点可能有多个孩子节点。在染色的过程中,本质是父子节点满足条件就染成红色。具体染色策略以下图为例
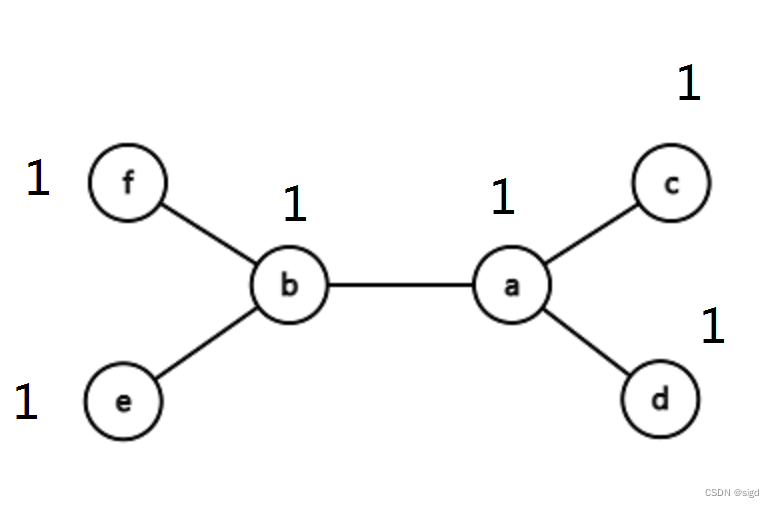
图中节点权值均为1,也就是任意相邻节点都可以满足染色条件,显然我们不能先将a和b染色,那样就只有2个点能被染色,而是应该先染色<f,b>或 <e,b>,然后再<a,c> 或<a,d>,这样可以染4个点。下图又该先考虑染色那些节点呢?
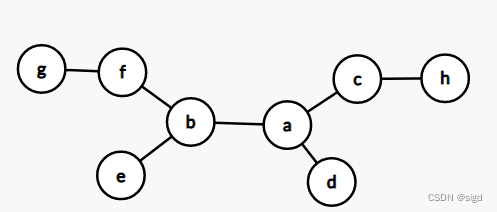
这样总结出贪心策略:先处理叶子结点的染色,然后处理内部节点。比如上图,先处理<g,f>。如果能染色,哪么将g,f标记红色,同时<f,b>就不可能染色了如果不能染色,未来还可以继续试探<f,b>。
实现方法:先处理最外层节点(叶子),外层处理完了,这些叶子就可以不要了,往内层推进。
使用拓扑排序的思想。当然不是入度0节点入队,这可不是有向图。而是度为1(叶子)节点入队,从树叶向树根进行拓扑处理。
图问题的复杂度正常都是遍历所有的结点,也就是访问所有的点和边,此图n-1条边,复杂度为O(n)。
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll n,a[100005],d[100005],red[100005],v[100005],ans=0;
vector <int> e[100005];
bool isP(ll x)/**< 平方数判定 */
{ll y=(int)sqrt(x);return y*y==x;
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y;cin>>n;for(i=1;i<=n;i++)cin>>a[i];for(i=1;i<n;i++){cin>>x>>y;e[x].push_back(y),e[y].push_back(x);d[x]++,d[y]++;/**< d数组统计度 */}queue<int>q;for(i=1;i<=n;i++)if(d[i]==1)/**< 度为1的入队*/q.push(i);while(q.size())/**< 模拟拓扑排序处理方法 */{x=q.front();v[x]=1;/**< 标记这个节点,避免重新被入队处理 */q.pop();for(i=0;i<e[x].size();i++)/**< 找到x所有邻接点 */{y=e[x][i];if(v[y]) /**< y已经访问过,其实y一定是x的子节点 */continue;if(red[x]==0&&red[y]==0&&isP(a[x]*a[y]))/**< x和它父节点y满足条件 */red[x]=red[y]=1,ans+=2;/**< 标记颜色,计数器+2 */d[y]--;if(d[y]==1)/**< 度为1说明y子节点都处理完了,此时可以入队 */q.push(y);}}cout<<ans;return 0;
}相关文章:

小美的树上染色
美团2024届秋招笔试第一场编程真题 先提一个小知识:题目中凡是提到树结构都要使用图的存储方式,只有二叉树例外。 分析:在树结构中,孩子和父节点是相邻节点,而父节点可能有多个孩子节点。在染色的过程中,…...

1.rk3588的yolov5运行:pt_onnx_rknn转换及rknn在rk3588系统python运行
自己有点笨,查资料查了一周才完美的实现了yolov5在rk3588环境下的运行,在这里写具体步骤希望大家少走弯路。具体步骤如下: 一、yolov5的原代码下载及pt文件转换为onnx文件 1.yolov5的原代码下载及环境搭建 在这里一定要下载正确版本的源代码…...
适用于全部安卓手机的 5 大免费 Android 数据恢复
您是否面临这样一种情况,即在Android设备上丢失了一些重要文件,但不知道应该选择哪种Android数据恢复来取回它们? 如果您以前从未备份过Android数据,则很难解决问题。 本文将介绍排名前5位的免费Android数据恢复软件。 您可以获…...

【案例分享】BenchmarkSQL 5.0 压测 openGauss 5.0.0
一、前言 本次BenchmarkSQL 压测openGauss仅作为学习使用压测工具测试tpcc为目的,并不代表数据库性能如本次压测所得数据。实际生产性能压测,还需结合服务器软硬件配置、数据库性能参数调优、BenchmarkSQL 配置文件参数相结合,是一个复杂的过…...

Linux之 4 种休眠模式
目录 1. Linux之 4 种休眠模式 1. Linux之 4 种休眠模式 # echo standby >/sys/power/state //CPU和RAM在运行 # echo mem > /sys/power/state //挂起到内存(待机),关闭硬 盘、外设等设备 # echo disk > /sys/power/state //挂起到硬盘(休眠),关闭硬盘、外设等设备&…...
homeassiant主题
下载主题 https://github.com/maartenpaauw/home-assistant-community-themes.git 使用file editor到homeassiant路径下,新建文件夹themes文件夹,用terminal新建也可以。 使用file editor上传文件 使用Terminal解压 mkdir themes unzip home-assistan…...

《2020年最新面经》—字节跳动Java社招面试题
文章目录 前言:一面:01、Java基础知识答疑,简单概述一下?02、倒排索引了解吗?使用Java语言怎么实现倒排?03、详细讲解一下redis里面的哈希表,常用的Redis哈希表命名有哪些,举例说明其…...

2.3IP详解及配置
2.3IP详解及配置 一、ip地址组成 IP地址由4部分数字组成,每部分数字对应于8位二进制数字,各部分之间用小数点分开 这是点分 2进制 如果换算为10进制我们称为点分10进制. 每个ip地址由两部分组成网络地址(NetID)和主z机地址(HostID).网络地址表示其属于…...

Python程序打包指南:手把手教你一步步完成
最近感兴趣想将开发的项目转成Package,研究了一下相关文章,并且自己跑通了,走了一下弯路,这里记录一下如何打包一个简单的Python项目,展示如何添加必要的文件和结构来创建包,如何构建包,以及如何…...

Linux yum 使用时提示 获取 GPG 密钥失败Couldn‘t open file RPM-GPG-KEY-EPEL-7
资料 错误提示: no crontab for root - using an empty one 888 原因剖析: 第一次使用crontab -e 命令时会让我们选择编辑器,很多人会不小心选择默认的nano(不好用),或则提示no crontab for root - usin…...

OpenGL_Learn13(材质)
1. 材质 cube.vs #version 330 core layout (location 0) in vec3 aPos; layout (location 0 ) in vec3 aNormal;out vec3 FragPos; out vec3 Normal;uniform mat4 model; uniform mat4 view; uniform mat4 projection;void main() {FragPosvec3(model*vec4(aPos,1.0));Norma…...

buildadmin+tp8表格操作(1)----表头上方添加按钮和自定义按钮
buildAdmin 的表头上添加一些按钮,并实现功能 添加按钮 <template><!-- buttons 属性定义了 TableHeader 本身支持的顶部按钮,仅需传递按钮名即可 --><!-- 这里的框架自带的 顶部按钮 分别有 刷新 , 添加, 编辑&…...

MySQL 定时计划任务 事件的使用
目录 查看事件是否开启 开启事件 1)通过设置全局参数修改 2)更改配置文件 MySQL如何创建并执行事件? 例 1 MySQL查看事件状态信息 MySQL修改和删除事件 例 1 例 2 删除事件 例 3 在数据库管理中,经常要周期性的执行某…...

C++构造函数 拷贝构造函数 括号法显示法隐式转换法实现类
一.无参构造 & 有参构造 & 拷贝构造函数 拷贝的是自己所属的类,也就是克隆自己。 所以传参要穿自己的类名。 克隆归克隆,但是不能把本身给改了,所以参数前要加const。class Person { public:int age;public:Person(){cout<<&q…...

FreeRTOS中的内存分配策略
FreeRTOS为内存管理提供了几种不同的策略,分别由heap_1.c至heap_5.c实现。以下是每种策略: heap_1.c: 最简单的策略。只允许一次性的内存分配。不允许内存释放。对于只分配内存但不释放的系统特别有用,如仅在启动时分配任务和队列的系统。内存…...
HP惠普光影精灵7笔记本Victus by HP 16.1英寸游戏本16-d0000原装出厂Windows11.21H2预装OEM系统
下载链接:https://pan.baidu.com/s/1LGNeQR1AF1XBJb5kfZca5w?pwdhwk6 提取码:hwk6 可适用的型号: 16-d0111tx,16-d0112tx,16-d0125tx,16-d0127tx,16-d0128tx,16-d0129tx&#…...
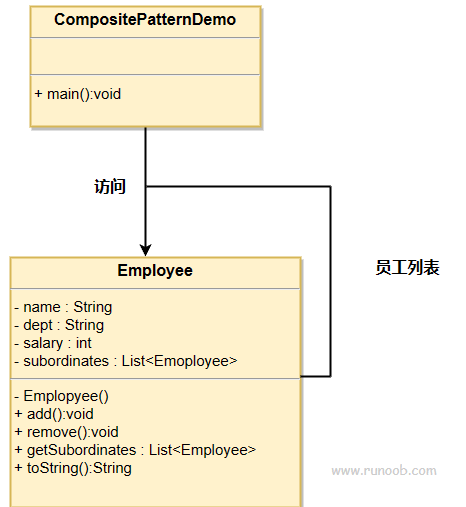
组合模式 rust和java的实现
文章目录 组合模式介绍实现javarsut 组合模式 组合模式(Composite Pattern),又叫部分整体模式,是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象,用来表示部分以及整体层次。这种类型的设计…...

大数据基础设施搭建 - MySQL
文章目录 一、检查是否安装过MySQL二、上传安装包三、安装MySQL3.1 安装mysql依赖3.2 安装mysql-client3.3 安装mysql-server 四、启动MySQL五、配置MySQL5.1 修改密码(1)查看密码(2)登陆(3)设置复杂密码&a…...

二叉树递归遍历
能帮到你的话,就给个赞吧 😘 二叉树遍历算法 指遍历一遍二叉树就能得到答案 什么是二叉树遍历 二叉树遍历 前中后序遍历 递归遍历 3种时间节点 递归遍历会依次遍历到每个节点。 而前中后序则是在递归遍历的基础上选择操作发生的时间。 递归遍历 …...
【ArcGIS Pro二次开发】:CC工具箱1.1.1更新_免费_安装即可用
CC工具箱1.1.1更新【2023.11.15】 使用环境要求:ArcGIS Pro 3.0 一、下载链接 工具安装文件及使用文档: https://pan.baidu.com/s/1OJmO6IPtMfX_vob3bMtvEg?pwduh5rhttps://pan.baidu.com/s/1OJmO6IPtMfX_vob3bMtvEg?pwduh5r 二、使用方法 1、在下…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
